随机微分方程平衡θ-Heun方法的稳定性

康红喜, 张引娣, 蒋 茜

(长安大学 理学院,陕西 西安 710064)

随着随机微分方程在金融、生物、工程技术等领域应用变得越来越多,对于随机微分方程的数值解的要求也越来越高。为了满足各个领域的需求,学者们提出了许多求解随机微分方程的数值方法，文献[1-8]给出了常见数值方法相关的研究成果。

求解微分方程的方法还有Heun方法,但是该方法对步长是有要求的,学者们的研究相对较少。Heun方法在文献[9]中被提出来后,文献[10-11]研究了该方法收敛性与稳定性的条件。另外,求解刚性随机微分方程对步长的要求更为苛刻,为了解决这一问题,文献[12]提出了一种全隐式的方法,又称平衡法。文献[13-15]对这个全隐式方法作了进一步研究,得到了该方法的渐近稳定性、均方稳定性以及高阶收敛性。本文提出了一个平衡θ-Heun方法,该方法结合了平衡方法与文献[16]中θ-Heun法的优点。本文研究该方法的均方稳定性和指数稳定性，并比较3种Heun方法的稳定性。

1 随机微分方程及数值方法

1.1 随机微分方程

考虑d维标量自治随机微分方程

(1)

其中:t∈[0,T];x∈Rd;函数f(x)为漂流项,函数g(x)为扩散项,两者在[0,T]上都是连续可测的,且有E|x0|2<∞;W(t)为一维标准布朗运动。设h为步长,当t>0,h>0时,其增量ΔW(t)=W(t+h)-W(t)服从正态分布N(0,h)。本文只研究方程(1)的一个类型,即带乘性噪音的随机微分方程。另外迭代式xn+1=R(λ,μ,h,ΔWn)xn是本文用数值方法求解随机微分方程得到的。

1.2 数值方法

1.2.1 θ-Heun方法

θ-Heun方法计算公式[16]为:

xn+1=xn+(1-θ)f(xn)h+θf(xn+hf(xn))h+g(xn)ΔWn。

1.2.2 平衡法

平衡法计算公式为[17]:

xn+1=xn+f(xn)h+g(xn)ΔWn+Cn(xn-xn+1)，

其中,Cn=c0(tn,xn)h+c1(tn,xn)|ΔWn|,函数c0、c1称为控制函数。

1.2.3 平衡θ-Heun方法

定义1 令h=T/N,tn=nh,n=0,1,…,N,称

xn+1=xn+(1-θ)f(xn)h+g(xn)ΔWn+θf(xn+hf(xn))h+Cn(xn-xn+1)

(2)

是平衡θ-Heun方法。其中:θ∈[0,1];Cn=c0(tn,xn)h+c1(tn,xn)|ΔWn|,特别地,当θ=0时,(2)式就是平衡隐式方法。根据文献[15],若要保证系统的稳定性,则这里的c0、c1是有界的d×d的实值矩阵值函数,满足可逆矩阵

M(t,x)=I+α0c0(t,x)+α1c1(t,x),

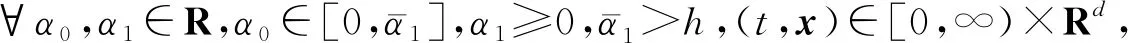
|M(t,x)-1|≤K<∞

(3)

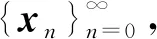
E|xn|2≤NE|x0|2e-mnh, ∀n≥0

(4)

成立,则称数值方法是指数稳定的。

2 平衡θ-Heun方法的稳定性分析

为了能够更简便地研究数值方法的稳定性,引入下面的随机微分方程,即

(5)

其中:t∈[0,T];λ,μ∈R;x∈Rd;W(t)为一维标准布朗运动。

将平衡θ-Heun方法用于(5)式得到如下的差分方程:

xn+1=xn+λhxn+θλ2h2xn+μxnΔWn+Cn(xn-xn+1)

(6)

其中,Cn=c0h+c1|ΔWn|,这里假设c0、c1为常数,步长为h=T/N,T=Nt,tn=nh,n=0,1,…,N。

2.1 d维随机微分方程MS稳定条件

定理1 用平衡θ-Heun方法求解线性随机微分方程(5)时,若有:

则方程(5)是MS稳定的。

证明首先将差分方程(6)写成下面的形式:

xn+1=(1+Cn)-1[(1+λh+θλ2h2+μΔWn)+Cn]xn=(1+Cn)-1[(1+λh+θλ2h2+μΔWn)+c0h+c1|ΔWn|]xn

(7)

根据(3)式有:

(8)

将(7)式、(8)式两边同时取均值可得:

(9)

(10)

其中

2K2E((c1+μ)|ΔWn|)2。

递推(10)式,要使Sn→0(n→∞),只需

根据期望的定义及积分性质可得:

即

1-2K2(1+λh+θλ2h2+c0h)2。

因此，若要方程(5)是MS稳定的,则只需:

下面取特殊的参数,c0=-λ/2,c1=0,当方程(5)为一维时,证明平衡θ-Heun方法MS稳定的具体条件以及平衡θ-Heun方法的指数稳定性。

2.2 平衡θ-Heun方法的MS稳定性

q<-(θ2p4+θp3+2θp2+2p),

则平衡θ-Heun方法是MS稳定的。其中:p=λh;q=μ2h。

证明由(6)式可得:

(11)

(11)式中取c0=-λ/2,c1=0,令p=λh,q=μ2h,则有:

(12)

对(12)式两边同时平方取均值,由E(ΔWn)=0,E(ΔWn)2=h可得:

(13)

整理(13)式可得:

q<-(θ2p4+θp3+2θp2+2p)。

此时平衡θ-Heun方法是MS稳定的。

2.3 平衡θ-Heun方法的指数稳定性

定理3对于方程(5),当c0=-λ/2,c1=0时,平衡θ-Heun方法是指数稳定的,当且仅当有下面的不等式成立,即

证明将c0=-λ/2,c1=0带入(6)式,可得:

(14)

对(14)式两边分别平方取均值,由E(ΔWn)=0,E(ΔWn)2=h,可得:

(15)

记

则(15)式经过递推可得:

(16)

当c0=-λ/2,c1=0时,求解方程(5)的平衡θ-Heun方法是指数稳定的,则根据定义3有:

E|xn|2≤NE|x0|2e- mnh, ∀n≥0。

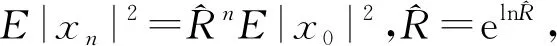
若想得到不等式

则需要找到一个n,使得:

(17)

又由:

(18)

结合(16)式、(18)式可得:

E|xn|2≤NE|x0|2e- mnh, ∀n≥0,

则当c0=-λ/2,c1=0时,平衡θ-Heun方法是指数稳定的。

3 数值实验

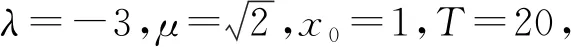
平衡θ-Heun方法、Heun方法、θ-Heun方法的MS稳定性如图1所示。

图1 3种方法的MS稳定性

从图1可以看出,平衡θ-Heun方法的稳定性最好,且对给定的3个步长都是MS稳定的;而Heun方法、θ-Heun方法的稳定性较差,只有h=1/4时才保证了方法的稳定性。通过对比可知，3种数值方法中平衡θ-Heun方法对步长的要求最低。 下面进行理论分析与验证。

(1) 对于图1a,设

θλ3h3+θ2λ4h4+μ2h,

当步长为h=1,h=1/2,h=1/4时,对应的值为:

由定义2可知，对于3个步长,平衡θ-Heun方法都满足MS稳定条件。

(2) 对于图1b,设

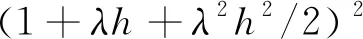
当步长为h=1,h=1/2,h=1/4时,对应的值为:

由定义2可知，当h=1/4时,Heun法才满足MS稳定的条件。

(3) 对于图1c,设

c=(1+λh+θλ2h2)2+μ2h,

当步长为h=1,h=1/2,h=1/4时,对应的值为:

由定义2可知，当h=1/4时,θ-Heun方法满足MS稳定的条件。

4 结 论

本文将平衡法的思想与θ-Heun方法结合起来,得到了平衡θ-Heun方法,研究了该方法用于d维随机微分方程(5)系统稳定的条件;在给定合适的控制参数时,对于一维线性随机微分方程,得到了保证平衡θ-Heun方法MS稳定的条件以及指数稳定的条件。从最后的数值算例中可以看出,平衡θ-Heun方法在3种数值方法中对于步长的要求最低。