基于应变硬(软)化模型的深埋巷道开挖对邻近巷道的影响
2021-03-15袁海平吕文涛陈承浩汪亦显王昱博乐彪华
袁海平, 吕文涛, 陈承浩, 汪亦显, 王昱博, 乐彪华
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
深埋工程在开挖过程中会出现围岩应力重分布现象,并引起围岩变形,且随着变形的发展,围岩的强度参数会出现明显的增大或减小现象,岩体可能发生失稳破坏,即所谓的围岩硬(软)化现象[1]。目前关于岩石的硬(软)化特性的研究大致可以分为2类:① 从岩石裂隙发育的微观角度,通过现场测试和室内试验相结合的方法,研究岩石产生应变硬(软)化特性的本质机制,这类研究对于探究岩石内在的变形损伤机制具有重要意义,但其成果很难运用到工程实践中;② 从宏观角度,利用连续介质力学理论建立岩石应变(硬)软化连续力学模型来描述岩石应变软化力学特性[2-3]。
对于应变硬(软)化模型,国内外已有一些研究成果。文献[4]在岩石三轴试验基础上,提出了强度退化指数的概念,用岩石峰后退化指数来研究峰后的软化行为;文献[5]利用文献[4]提出的峰后强度退化指数,与Mohr-Coulomb准则结合,建立了考虑围压影响的岩石峰后应变软化力学模型;文献[6]采用 Hoek-Brown 准则和弹塑性理论,研究围压对软岩峰后软化特性的影响,以及软岩峰后宏观物性参数的应变软化规律,建立了峰后应变软化数值模型;文献[7]基于 Hoek-Brown 准则和 Mohr-Coulomb 准则提出了岩石峰后应变软化模型;文献[8]对三峡花岗岩进行了常规三轴压缩试验,并基于弹塑性理论,研究花岗岩强度参数与峰后应变软化参量的关系,建立了花岗岩的峰后应变软化模型;文献[2]通过对软弱泥岩进行常规三轴压缩试验,研究了对软弱岩石的峰后应变软化力学特性,依据 Mohr-Coulomb屈服准则,得出软弱岩石峰后力学参数的软化规律;文献[9]结合Mohr-Coulomb强度准则和非关联流动法则对岩石在三轴试验中呈现的应变软化行为进行了分析,获取了峰值前、后强度参数的大小。
上述研究成果还存在以下不足:① 对岩石强度的真实硬(软)化规律做了很多简化与假设,导致结果与实际出现偏差;② 没有考虑峰前硬化阶段对模型的影响,建立的应变硬(软)化模型不合理。本文在已有研究基础上,选取特定的硬(软)化参数η[10],结合等向硬(软)化规律和塑性流动法则,获取了岩石强度参数随硬(软)化参数的变化规律,建立了岩石的应变硬(软)化模型,并将岩石应力-应变关系简化,代入 FLAC3D软件内置应变硬(软)化本构关系中,对深埋巷道开挖对邻近巷道的影响问题进行研究。
1 应变硬(软)化模型
硬(软)化规律是材料在加载过程中加载面的形状、大小及位置的变化规律,这在宏观上表现为材料的硬(软)化,在塑性力学中则表现为屈服面的变化,因而岩石类材料的屈服准则可用一组屈服面表示。本文以Mohr-Coulomb准则作为屈服准则,但其c值和φ值不再是常数,而是随塑性变形的发展而变化。一组屈服面的表达式为:
(1)
其中:σ1为最大主应力;σ3为最小主应力;φ为内摩擦角;c为黏聚力。
目前屈服面的变化规律还不能完全确定,需要对屈服面的运动与变化规律做一些假设,选用硬(软)参数η来表征材料硬(软)化的程度,反映材料硬(软)化的历史。下面依据Mohr-Coulomb屈服准则和等向硬(软)化规律对材料状态进行分析[11-12],使用内变量η代表加载历史,c、φ看作η的函数。岩石应力-应变曲线如图1所示。图1中,εs为屈服点应变,εp为峰值点应变,εr为残余阶段初始点应变。以图1a典型应力-应变曲线为例,当η=0时,c=c(0),φ=φ(0),屈服面为初始屈服面,材料处于εs之前的弹性阶段;随着η不断增长,屈服面不断扩大,材料处于硬化阶段;当η达到峰值ηp时,c=c(ηp),φ=φ(ηp),屈服面达到峰值屈服面;随着η进一步增长,屈服面逐渐收缩,材料处于软化阶段,意味着已达到破坏状态,以致在η=ηr(ηr为残余阶段初始处η值)时,屈服面达到最终屈服面,材料进入残余应力阶段。图1b为简化后的应力-应变曲线,即为理想状态下的应变硬(软)化模型。
2 应变硬(软)化模型中的参数
2.1 硬(软)化参数
硬(软)化参数η通常有2种不同的形式,一种是内在变量的形式,另一种是塑性应变增量的形式,但至今没有被广泛接受的形式[13]。FLAC3D中的应变硬(软)化模型采用塑性剪应变εps控制强度参数变化[14],其增量形式定义为:
(2)
(3)
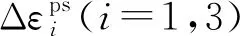
本文基于强度参数随着最大主应变的增加而变化这一规律,采用二维塑性剪应变γp作为硬(软)化参数,γp形式简单、物理意义明确,与εps之间可以相互转化,其表达式为:
(4)
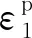
由塑性势理论可知,岩土体材料存在塑性势函数g,该塑性势函数与屈服准则形式不同,势函数对应于非关联流动法则[11-12],其表达式为:
g(σ1,σ3,η)=σ1-K(η)σ3
(5)
K(η)=(1+sinψ)/1-sinψ
(6)
其中,ψ为剪胀角,本文在相关研究[10,15-17]基础上,认为ψ取值比φ小20°。对应的塑性非关联流动法则为:
(7)
其中:λ为非负的参数;dεp为塑性应变增量。
分别对最大、最小主应力进行偏微分,得到:
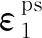
(8)
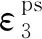
(9)
将(8)式、(9)式代入(2)式,可得:
(10)
(11)
由(4)式、(10)式、(11)式,η与εps关系可表示为:
(12)
2.2 强度参数演化规律
一般可通过试验、数值模拟或现场观测等方法来获取强度参数ω(包含c、φ等)与η之间的关系,即ω演化规律。为了使问题简化,假设ω与η之间为分段线性函数的关系,其简化后的表达式为:
(13)
其中:ω0为初始强度参数;ωp为峰值强度参数;ωr为残余强度参数。
3 深部巷道开挖稳定性研究
3.1 数值模型描述
2条埋深600 m的平行直墙拱形巷道,墙高为4.0 m,拱高为 2.0 m,宽度为 4.0 m,2条巷道中心距为16 m,影响范围取长、宽、高分别为30 、50 、40 m,采用 FLAC3D 软件对巷道开挖稳定性进行模拟分析,计算模型如图2所示(节点数目为115 371个,单元数目为683 329个)。在巷道1内沿x轴方向每隔1 m布置1组监测点,每组监测点布置如图3所示。
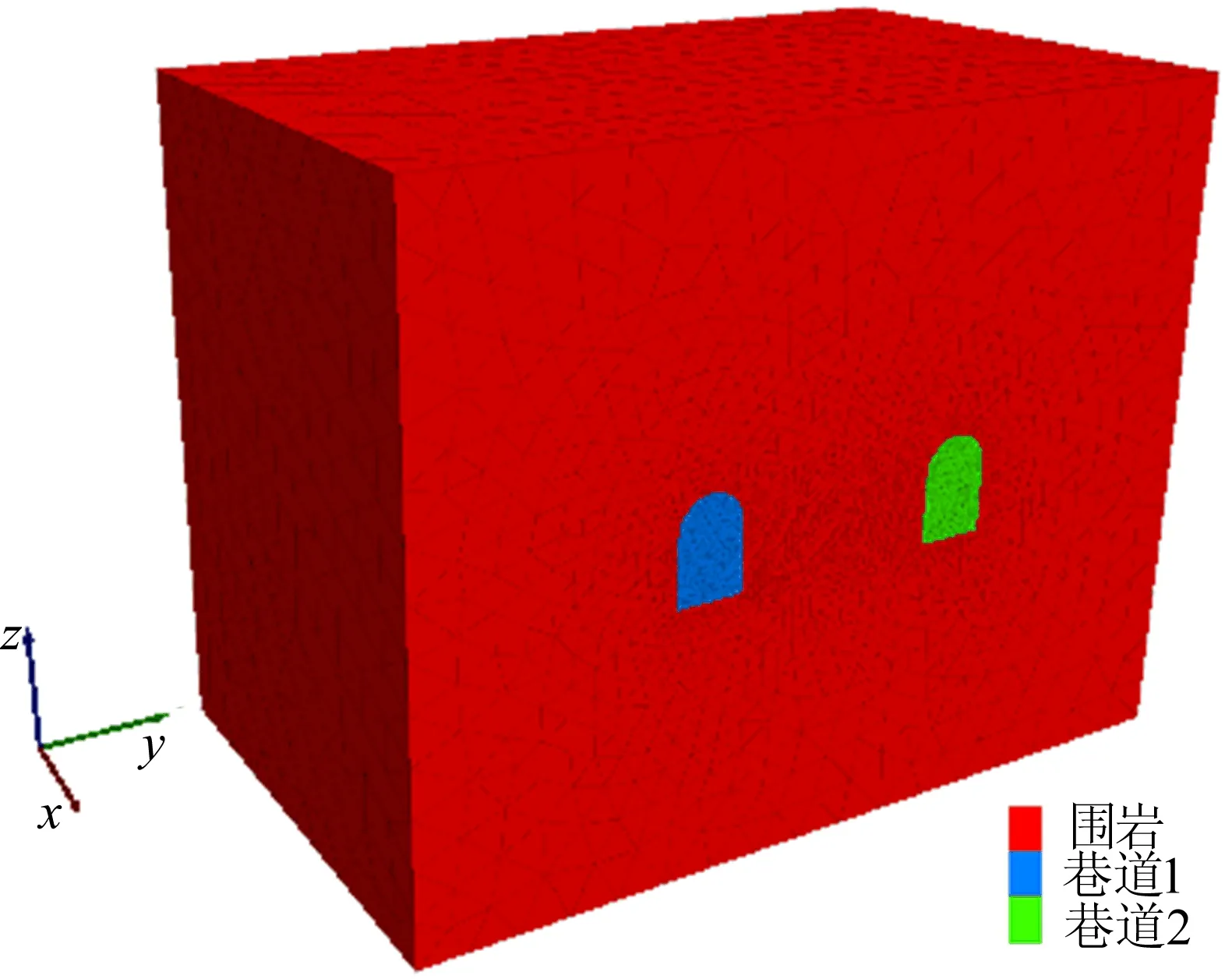
图2 计算模型
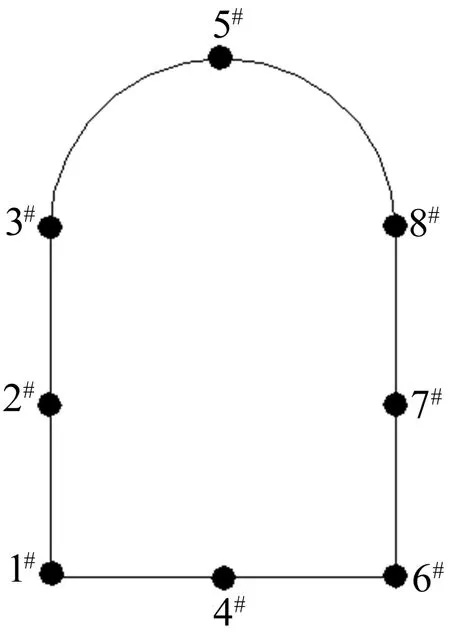
图3 巷道断面监测点布置示意图
模型主要模拟了在垂直应力σv=21 MPa,水平应力σh=42 MPa的高水平应力条件下,巷道开挖对邻近巷道产生的影响(规定巷道开挖方向为x轴负轴方向,每次开挖5 m)。对模型四周和底部边界进行法向约束,顶面施加大小为21 MPa的均布荷载(方向沿z轴负轴)。计算参数主要来源于Tennessee大理岩三轴试验数据[4-5,18],具体岩体力学参数见表1、表2所列。

表1 岩石力学参数
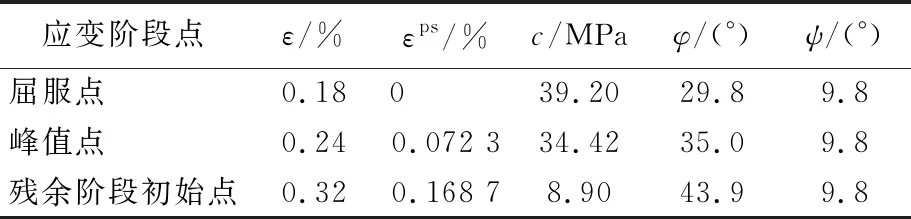
表2 岩石强度参数
3.2 巷道稳定性分析
为分析巷道2开挖对巷道1的影响,本文从围岩的应力、位移及产生的塑性损伤区等方面,对巷道的稳定性及安全性进行评估。
开挖完成后x=15 m剖面应力云图如图4所示(单位为Pa)。
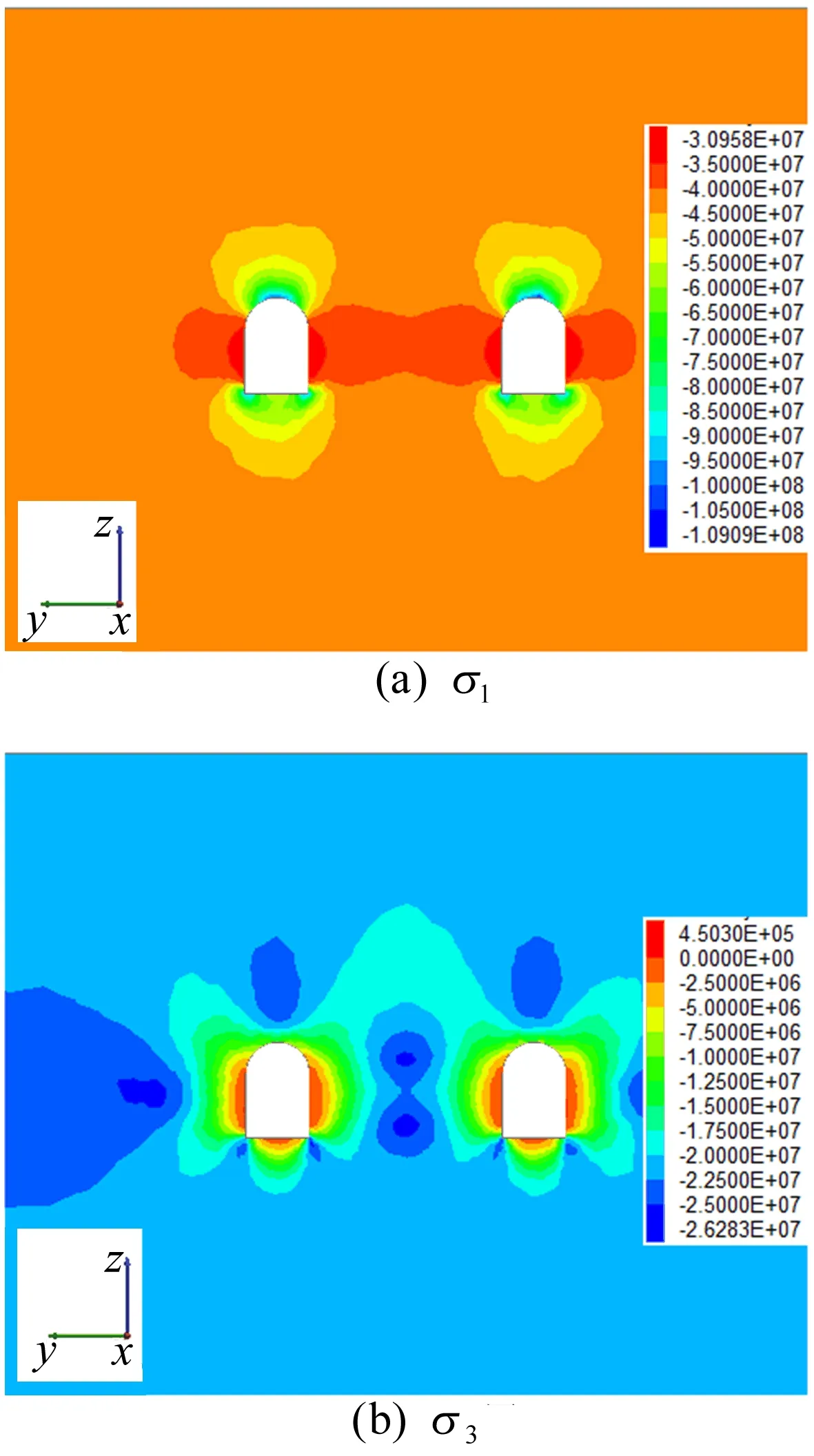
图4 开挖完成后x=15 m剖面应力云图
从图4a可以看出,围岩最大主应力σ1均为压应力,在底板两侧及拱顶出现应力集中现象,应力值较大,分布区域较小,但两侧墙中部应力值较小,分布区域相对较大。从图4b可以看出,围岩最小主应力σ3从外侧向巷道内部逐渐减小,除两侧墙及底板部分区域受拉外,其余均部分受压。
开挖完成后,x=15 m处巷道1两侧不同位置应力值如图5所示。
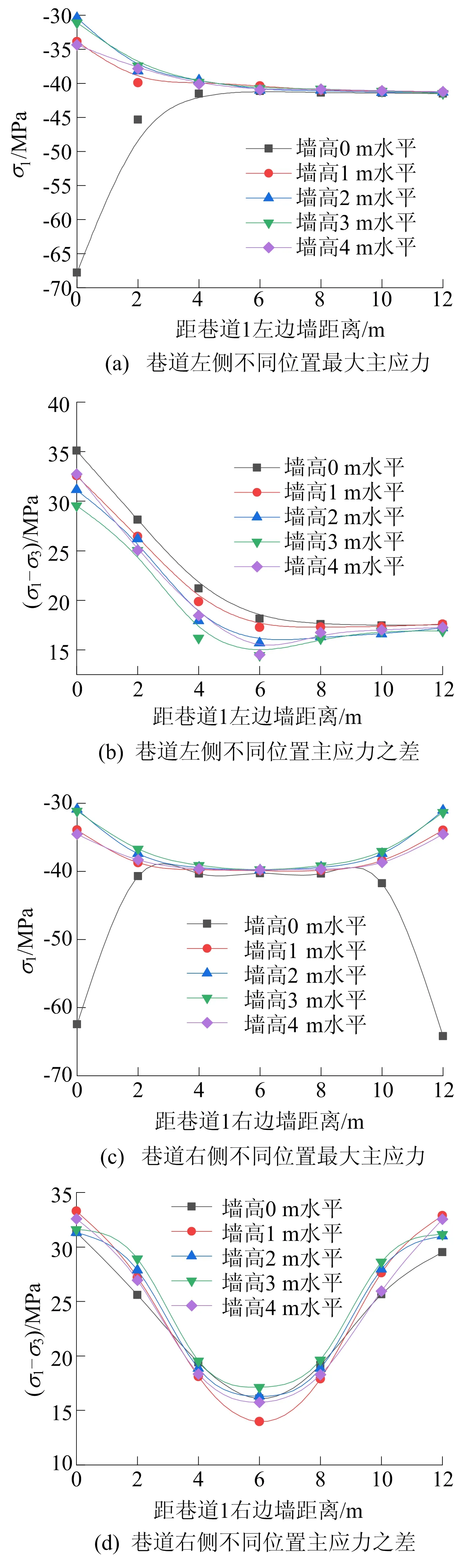
图5 开挖完成后x=15 m处巷道1两侧不同位置应力值
从图5a、图5c可以看出,随着与巷道距离增大,σ1趋于稳定,但越接近巷道,围岩发生的应力重分布现象越明显,靠近底板处出现应力集中现象,巷道右侧(即2条巷道之间)区域应力大小对称分布,中间位置应力值较大,这是2条巷道相互作用的结果。从图5b、图5d可以看出,随着与巷道距离增大,主应力之差σ1-σ3趋于稳定,但越接近巷道,σ1-σ3越大,巷道越容易发生破坏。综上所述,巷道开挖影响的范围大概是1~2倍的巷宽,且越接近巷道的位置围岩应力扰动越大,越容易发生破坏。
经分析,巷道1开挖后,由于围岩应力释放、次生应力场重分布,在底板两侧及拱顶出现压应力集中现象,两侧墙出现拉应力区。而随着巷道2不断开挖,即随着掌子面的推进,巷道拱顶和底板压应力逐渐减小,而两侧墙中间部分区域拉应力减小,压应力增大,这是由于巷道2开挖后应力释放所致。
不同巷道断面上5#、2#监测点应力值随开挖步的变化规律如图6所示。
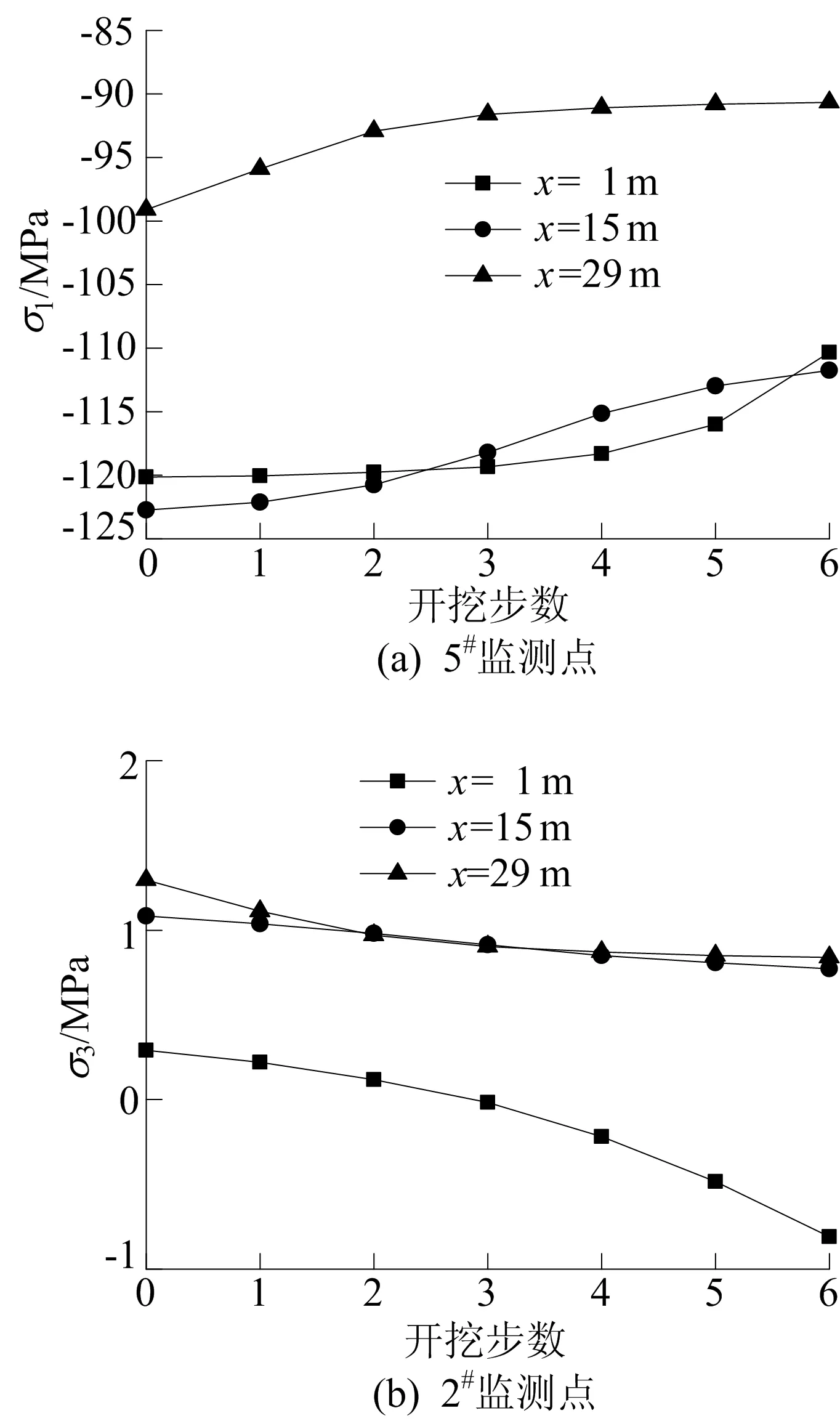
图6 5#、2#监测点应力随开挖步数的变化
从图6可以看出:随着巷道2不断开挖,巷道x=1 m处应力值的变化速度随着与掌子面距离减小而增大;x=29 m处应力值的变化速度随着与掌子面距离增加而降低。由此可知,随着巷道断面与掌子面距离增加,应力值变化速度逐渐降低。
开挖完成后x=15 m剖面位移云图如图7所示(单位为m)。从图7可以看出,巷道主要变形为两侧墙位置的横向变形,而拱顶沉降及底板隆起较小。经分析,随着巷道2不断开挖,即随着掌子面推进,围岩应力进一步释放、次生应力场重分布,除靠近巷道2右侧墙变形量减小外,其余位置变形量增大。巷道1两侧不同位置的位移如图8所示。从图8可以看出,随着围岩与巷道之间距离增大,位移逐渐减小,围岩较稳定。
以x=15 m处巷道断面为例,巷道1监测点位移随开挖步数的变化规律如图9所示。图9b中,n为开挖步数。从图9可形象直观地看出巷道断面各监测点位移及右侧墙位移曲线的变化规律,这为巷道变形量的预测及控制提供了参考。不同巷道断面上2#、7#监测点位移随开挖步数的变化规律如图10所示。从图10可以看出,随着巷道2不断开挖,巷道x=1 m处监测点位移的变化速度随着与掌子面距离减小而增大;x=29 m处监测点位移的变化速度随着与掌子面距离增大而降低。由此可知,随着巷道断面与掌子面之间距离增加,变形量的变化速率逐渐降低。
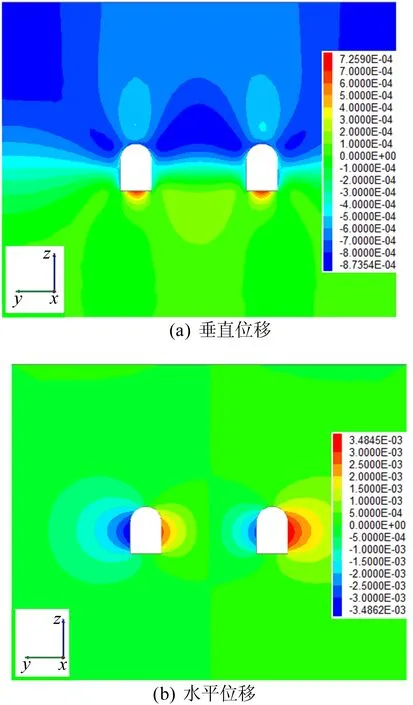
图7 开挖完成后x=15 m剖面位移云图
塑性区(暗色区域)分布如图11所示。从图11可以看出,塑性区分布范围较小,主要分布于两侧墙位置,且主要为受拉塑性区,这是由底板两侧及拱顶高的应力集中和侧墙的低应力导致的拉伸作用引起的。
不同开挖阶段塑性区体积变化如图12所示。从图12可以看出,随着巷道2不断开挖,总塑性区体积呈线性增大,而巷道1周边塑性区体积不变,因此巷道2的开挖对巷道1周边塑性区体积的变化基本无影响。
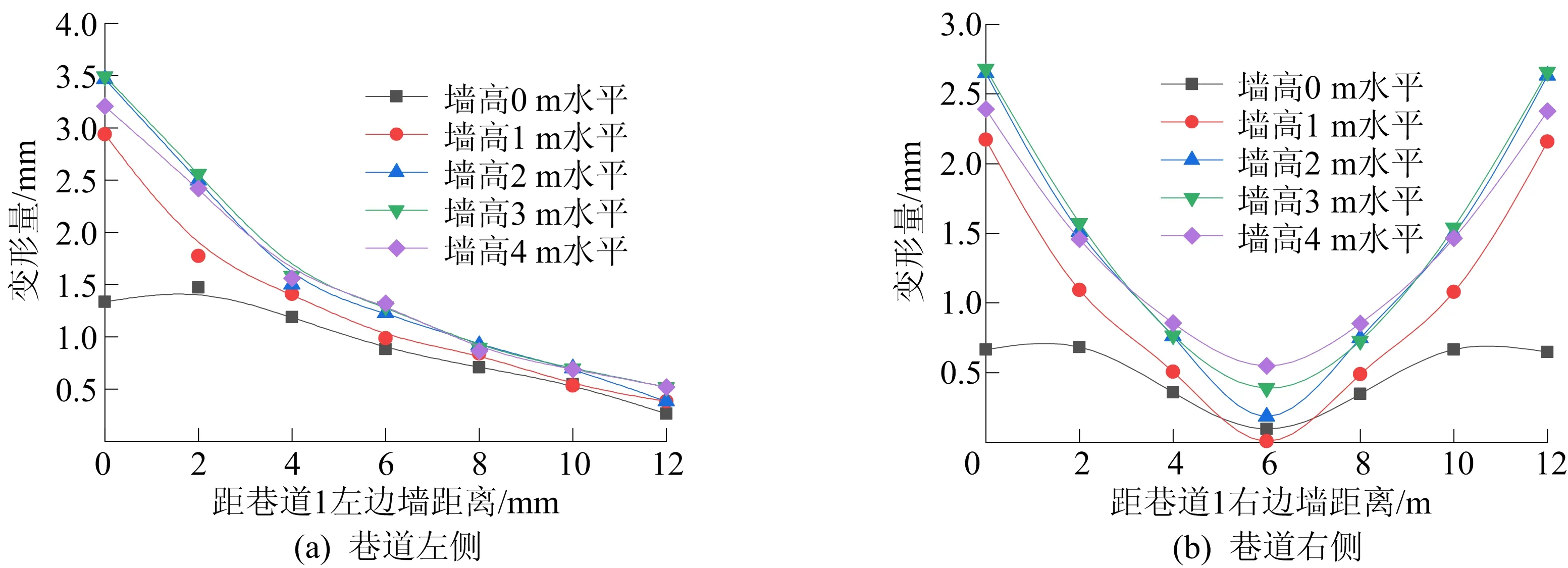
图8 开挖完成后x=15 m处巷道1两侧不同位置位移
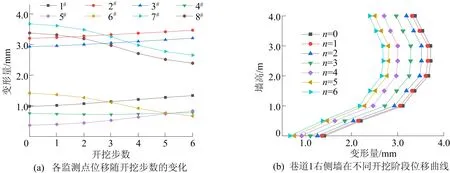
图9 x=15 m处监测点位移随开挖步数的变化
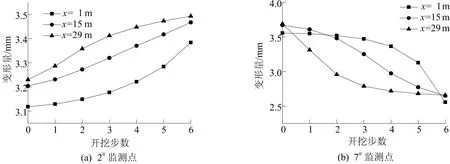
图10 2#、7#监测点位移随开挖步数的变化
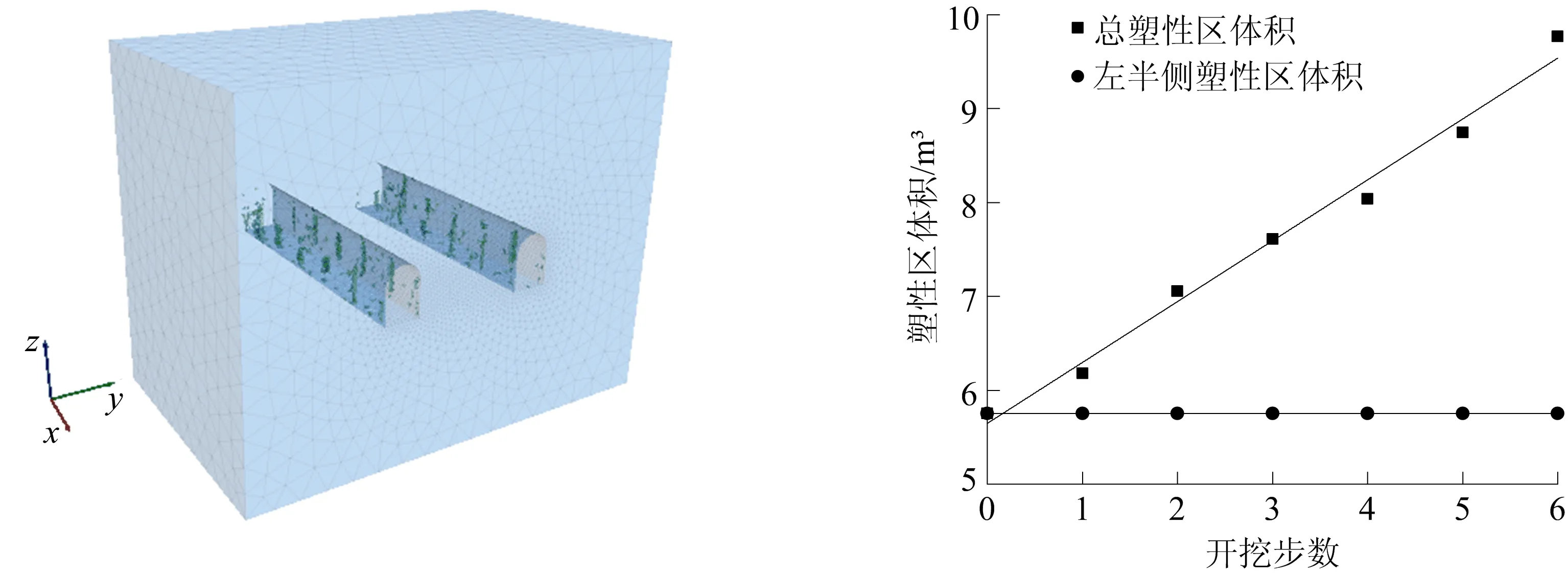
图11 塑性区分布 图12 塑性区体积随开挖步数的变化
4 结 论
本文基于应变硬(软)化模型对深埋巷道开挖对邻近巷道的影响问题进行数值模拟。从应力、位移及产生的塑性损伤区等方面进行分析,对巷道的稳定性及安全性进行评估,得出以下结论:
(1) 获取的岩石强度参数随硬(软)化参数的变化规律及建立的岩石应变硬(软)化模型能够反映岩石类材料的主要性质,对认识岩石强度演化规律有一定的指导意义。
(2) 中心距为16 m的2条平行巷道开挖产生的变形量和相关应力值的大小均在安全范围内,巷道在高水平应力条件下的潜在破坏区域主要分布在两侧墙、拱顶及底板两侧,该结果可为实际工程中巷道的支护设计和监测点的布置提供参考。
(3) 巷道内各位置应力值和变形量会随着邻近巷道开挖的进行而发生变化,且变化速率会随着与掌子面距离增加而降低,这是符合实际规律的,在一定程度上验证了采用应变硬(软)化模型对岩土工程问题进行数值模拟是准确可靠的。
