基于Mamdani模糊逻辑系统的一类未知混沌系统的同步控制

高子林, 刘志强， 王银河, 熊 江

(1.重庆三峡学院 智能信息处理与控制重点实验室,重庆 404100; 2.广东工业大学 自动化学院,广东 广州 510006)

由于混沌系统存在一些特有的性质,如对初始条件具有敏感性、存在奇异吸引子和相空间中的分形等,因此被广泛地应用在保密通信[1]、生物系统[2]、化学反应[3]及信息处理[4]等各个领域。特别地,自从文献[5]首次利用驱动-响应方法实现了混沌系统的同步控制以来,混沌系统的同步控制问题得到了广泛关注,并取得了一系列有价值的成果[6-9]。特别是在考虑混沌系统中存在不确定性和外部扰动的情况下,学者们提出了Backstepping控制[10]、自适应控制[11]、滑模控制[12]以及线性和非线性反馈控制[13]等智能同步控制方法。

文献[14]证明了模糊逻辑系统的万能逼近性,因此使用该系统来逼近混沌系统中未知非线性项成为可能[15-18]。文献[15-16]采用Mamdani自适应模糊逻辑系统来逼近混沌系统中的未知非线性函数。从数学的角度看,Mamdani型模糊逻辑系统的输出可以用一组模糊基函数的线性组合进行表示,文献[15-16]给出的参数自适应律主要用于对这组系数(实际上就是模糊规则中的后件参数)进行在线估计,因此参数自适应律的个数与组合系数的数量相等,即参数自适应律的个数由模糊规则的数目决定。在实际应用过程中,为了提高控制性能和精度,往往需要使用大量的模糊规则,这会导致使用大量的自适应律对模糊规则的组合系数进行估计,从而增加了在线计算时间,容易导致系统延时,甚至导致系统的不稳定。因此,在具备某些先验知识的情况下, 生成不带有组合参数自适应律的模糊逻辑系统来近似逼近实际工程中的非线性项是很有必要的。

不难看出,混沌系统中的未知非线性项可以用模糊逻辑系统近似逼近,并基于Lyapunov稳定性理论可以完成同步控制器的设计。然而,现有方法的前提条件是混沌系统中的参数要求是已知的,这在一定程度上限制了混沌系统在实际工程中的应用。另一方面,文献[19-21]考虑了混沌系统中存在未知参数的情况,采用自适应方法完成了同步控制器的设计,所提出的方法要求混沌系统中非线性项必须是已知的。

针对上述2种情况的缺陷,本文研究了一类完全未知的混沌系统的驱动-响应同步问题,其中未知非线性函数用不带参数自适应律的Mamdani型模糊逻辑系统进行近似逼近,未知参数则通过自适应方法进行在线估计,然后利用Lyapunov稳定性理论完成了同步控制器的设计,并给出了数值仿真,其结果验证了该方法的可行性和有效性。在同步控制器设计中, 参数自适应律的数目与模糊规则的数目无关,与文献[15-18]中的方法相比,本文提出的方法不仅可以减少在线计算量,而且更符合实际应用中对混沌同步的要求。

1 系统描述

考虑如下混沌系统作为驱动系统[22-23]:

(1)

针对系统(1)式,若选择非线性函数f1(x)=-x1x3,f2(x)=x1x2,当参数α=10、δ=28、γ=8/3、φ=1时,系统(1)式是一个典型的Lorenz混沌系统[23-24];当参数α=35、δ=-7、φ=-28、γ=3,系统(1)式则被称为Chen混沌系统[23,25];当参数α=36、δ=0、φ=-20、γ=3时,则称系统(1)式为Lü混沌系统[22-23]。因此,针对混沌系统(1)式的同步研究具有一定的代表性和广泛性。

混沌系统在保密通信[1]、化学反应[3]以及信息处理[4]等领域得到广泛地应用。近年来研究发现,同步电机(虚拟同步电机)的模型可以通过变换等效为一个类似于系统(1)式的Lorenz动态方程[25],在某些情况下,针对系统(1)式的研究可以为电力系统的可靠运行提供理论基础,进而有助于混沌系统在实际工程中的应用。

系统(1)式的响应系统如下:

(2)

如果定义状态同步误差为ei=yi-xi(i=1,2,3),那么通过系统(1)式和(2)式可得到如下误差微分方程:

(3)

记状态同步误差向量为e=[e1,e2,e3]T。

假设1 外界干扰|ζi(t)|≤ωi(t),|ξi(t)|≤σi(t)(i=1,2,3),其中已知函数ωi(t)和σi(t)在[0,+∞]是连续的。

2 系统设计

本文设计Mamdani型模糊逻辑系统用于逼近系统(1)式中的未知非线性函数,采用参数自适应方法对未知参数进行在线估计,利用其估计信息完成同步控制器的设计,最终实现一类完全未知混沌系统的驱动-响应同步。

2.1 Mamdani型模糊逻辑系统设计

基于模糊逻辑系统的万能逼近性,系统(1)式中的未知非线性函数fk(x)(k=1,2)可以用Mamdani型模糊逻辑系统进行近似逼近。现考虑使用带有Nk条模糊规则的Mamdani型模糊逻辑系统Fk来近似逼近fk(x),其模糊规则在论域W⊂R3中表示如下:

(4)

如果采用单点模糊化、乘积推理与中心解模糊,那么由模糊规则(4)式构成的模糊逻辑系统Fk的输出为:

k=1,2

(5)

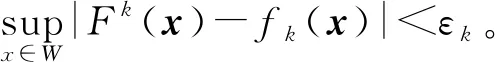
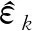
2.2 同步控制器设计

(6)

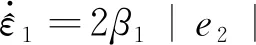
(7)

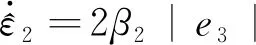
(8)

(9)

(10)

(11)

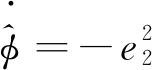
(12)

其中:es=b1e1+b2e2+b3e3;g为一个给定的正常数,且参数b1、b2、b3、g在选择时要保证矩阵

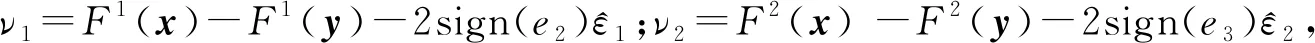
定理1 考虑系统(1)式和(2)式,若假设1成立,则在控制器(6)式和自适应律(7)～(12)式的作用下,可以达到控制目标的要求。

3 数值仿真

在仿真的过程中,假设参数α=10、δ=28、γ=8/3、φ=1和非线性函数f1(x)=-x1x3、f2(x)=x1x2均是未知的。首先用Mamdani模糊逻辑系统Fk(k=1,2)分别近似逼近未知非线性函数f1(x)=-x1x3和f2(x)=x1x2。变量x1、x2、x3的论域均为[-80,80],将论域划分成3个模糊集{负(N),零(Z),正(P)},其隶属度函数分别为μZ(z)=e-z2,μN(z)=e-(z+50)2/60,μP(z)=e-(z-50)2/60,根据某些先验知识,本文主要依据f1(x)与x1x3异号和f2(x)与x1x2同号的关系给出了模糊规则，见表1所列。

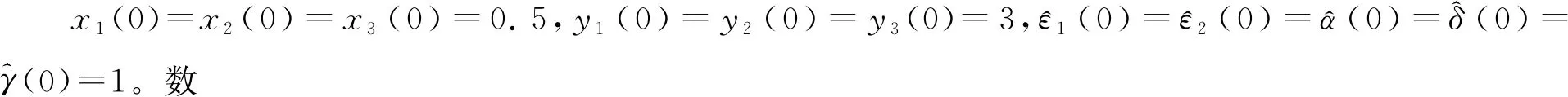
表1 用于近似逼近f1(x)和f2(x)的模糊规则

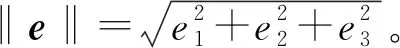
图1 状态x1和y1随时间变化曲线

图2 状态x2和y2随时间变化曲线

图3 状态x3和y3随时间变化曲线

图4 同步误差ei随时间变化曲线

图5 参数随时间变化曲线

图6 总同步误差‖e‖随时间变化曲线

综上所述,对于一类完全未知的驱动系统(1)式,在控制器(6)式和自适应律(7)式～(12)式的作用下,使响应系统(2)式与驱动系统(1)式实现了同步。由图4和图6可知,相比于文献[22]的同步方法,本文提出的方法可以使驱动系统和响应系统更快地实现同步;由图5可知,参数估计是在线进行的,并且每个参数都是有界的。因此本文提出的同步方法在工程应用中更具有实用性。

4 结 论

本文利用自适应方法和模糊逻辑系统的万能逼近性,针对一类完全未知的混沌系统给出了驱动-响应同步的控制方案。其中模糊逻辑系统仅用于近似逼近混沌系统中的未知非线性函数,自适应方法解决了参数在线估计的问题。在同步控制器的设计过程中,参数自适应律的个数与模糊规则的数目无关,且只有6个通用参数需要在线估计，自适应律的数目显著减少,在线运算量也随之减少,并且通过某些先验知识产生的模糊规则所构成的模糊逻辑系统(无需对模糊规则的后件参数进行在线估计)具有更广泛而高效的应用。