基于关联分析的学生成绩分析应用
2021-03-15曾庆涛唐明杰张孝良
黄 蕙, 曾庆涛, 唐明杰, 张孝良
(北京印刷学院信息工程学院,北京 102600)
1 大数据
1.1 相关概念
大数据最早应追溯到20 世纪,但只是在一些小范围的特殊行业进行应用,在影响力方面还很微弱。 2008-2012 年大数据应用才真正兴起。麦肯锡(McKinsey)公司将大数据在技术层进行定义:“大数据是具有快速的数据流转、价值密度低、海量的数据规模和多样的数据类型四大特点,是一种比传统数据库软件在获取、存储、管理、分析数据方面更优的大规模数据集合。”大数据因此被认为是具有 4V 的特征:一是数据的体积巨量(Volume),指数据能够不断增长并且规模十分完整;二是数据的种类繁多(Variety),指数据的形式多种多样,非结构化的数据占比日益突出;三是处理的速度十分迅速(Velocity),指数据流的处理迅速;价值密度低(Value),这些数据更多表现为稀缺性、不确定性和多样性。 如今大数据概念的范畴已经远超技术领域。 唐斯斯对大数据的解释是:“大数据要有自身的社会属性,就是指大数据受社会的影响而派生出来的属性,具体的表现是:权益多中心,数据将成为资产,所有者将拥有数据所有权;交互回应性;网络关联性和需求个性化四个方面。”
1.2 教育大数据
随着大数据技术的不断发展,大数据在教育领域的应用日益加深,教育大数据也随之产生。 作为大数据的一个子集、一个分支,目前国内对于教育大数据的内涵并没有一致的意见,其定义也不尽相同。 杨现民认为教育大数据是在整个教育的过程中自然产生的,然后根据教育的需要进行收集,从而全部用来促进教育发展,可以创造更多潜在价值的数据集。 孙洪涛把教育大数据定义为服务教育学科和教育过程,具有很强的周期性、很高的教育价值、很复杂的数据集合。 章怡等从教育大数据如何产生的角度将其界定为:信息技术支持下教与学各个环节所产生的符合教育大数据特征的数据集,是信息技术环境下教与学行为轨迹的产物。 胡凡刚则从教育虚拟社区角度出发,认为教育大数据是以学习为目的,学习者在网络学习环境中通过一定的媒体与外界进行互动,生成数据,包括学习行为、学习内容数据、虚拟社交网络数据和学习管理数据。
本文认为教育大数据有广义和狭义的区别,广义的教育大数据是指在教育领域内产生的一切数据;狭义的教育大数据是指在信息化环境下,教师和学生在教与学全过程中产生并被采集到有助于提高教学质量的数据集合。 在教育教学中充分利用教育大数据的价值,发挥其特点,帮助教师和学生去诊断教学中存在的问题,使得教育质量得到充分提高。 另外,利用教育大数据充分挖掘受教育者的潜力,对支持个性化的教与学提供巨大的帮助,使得因材施教成为可能。
2 数据挖掘
2.1 数据挖掘概念
在某些数据库当中自发生成有效信息的过程称为数据挖掘,也就是数据采矿、资料勘探。 数据挖掘是数据库中知识发现(KDD)不可缺少的一部分[1]。 这是一个过程,这个过程是要从数据中搜索出隐藏蕴涵的联系、信息等,与计算机科学有关,通常应用于统计、情报检索、机器学习等领域。
2.2 数据挖掘基本过程
数据挖掘基本步骤过程有:研究目标的确定、模型的选择、截取有效的数据、预处理所取数据、数据的挖掘、结果的分析、同化知识。 具体流程如图1 所示。

图1 数据挖掘流程图
数据进行处理之后才可以开始挖掘,数据挖掘便是利用预处理后的数据来快速获取对工作有用的知识的一个过程。 那么我们先要选择进行数据挖掘的研究目标,接着需要择优选用挖掘算法、运行算法进行多次的实验,最后对实验结构进行分析理解,这样才能获得我们需要的信息。
2.3 预处理数据
我们之所要对数据进行预处理,是因为有时直接截取的数据不适于挖掘,采取有效的预处理手段可以使得所截取数据更加适用于数据挖掘技术。挖掘前要将数据进行预处理,这项工作是一个相对比较广泛的技术领域。 对数据的预处理方法有许多,总体来说这些方法技术策略可以分为两种。 一是选择分析所需要的数据对象;二是属性及创建/改变属性。 以上所说的两种情况其目的都是有效改良数据挖掘的分析工作,可以减少工作时间,同时还可以降低成本并且提高工作质量。
2.4 数据挖掘方法
从20 世纪80 年代开始,数据挖掘逐步发展成熟,在几十年的技术发展过程中,研究者们在漫长的过程逐渐发现了许多方法,我们将其分成以下几类。
(1)分类
分类是找出数据库中一组数据对象的共同特点并按照分类模式将其划分为不同的类,其目的是通过分类模型,将数据库的数据项映射到某个给定类别。
(2)聚类分析
将所得数据分组为有利用价值的组(簇)。 如果组是有意义的,那么簇必须捕捉数据自然结构。但是,在不同方面的群体分析仅仅是解决其他问题的开始。 聚类分析在相当大的领域范围内都发挥着极其重要的作用,无论是在理解还是实用性方面。
(3)关联分析
此方法经常用来识别一些在数据集中隐秘的有用的连接关系。 用此方法来发现的关系可以表示为相关规则或者是频繁项集。
(4)偏差分析
这里所说的偏差其中包含大量的潜在知识,比如分类异常,模式异常和观察结果与预期偏差。 偏差分析发现实际值与理想值之间的偏差,寻找观察结果与参照量之间的显著差异。
(5)特征分析
顾名思义此策略便是寻找特征,一般在数据库当中的数据组中提炼出相关的特征,所得出的结果可以表示数据集的一般特征。
3 关联分析
3.1 关联分析的概念
(1)二元表示形式
以上案例我们可以通过二元形式更加形象易懂地表示出来,如表1 所示。 同理此表中同样是每一行对应一个事务,但是每一项用一列来表示。 如果某位顾客在一次购物中购买了某物品,则用1 来表示,否则用0 表示。
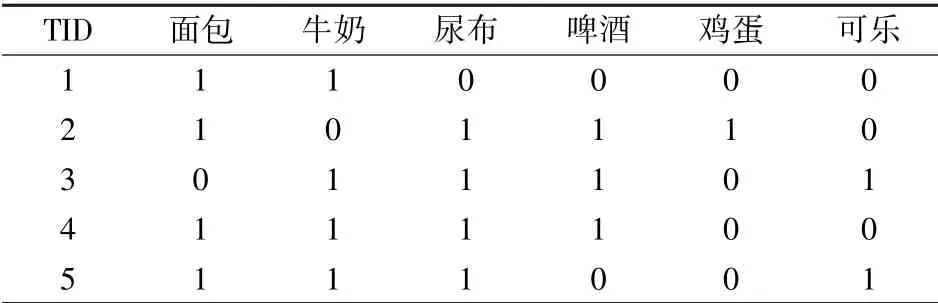
表1 购物篮数据的二元形式
(2)支持度计数与项集
一般来说我们会将P={p1,p2,…,pd}这个集合看作是数据集中的所有项集合;将Q={q1,q2,…,qn}看作是是事务集合,那么我们可以看出每一个qi中所包括的项集就是子集。 我们通常在关联规则中把含有大于0 项的所有集合I 叫作项集。 k-项集一般是说某个项集中含有k 项。 像在购物篮实例中{面包,牛奶}我们就叫它为2-项集。 所谓的空集就是指那些不含任意项项集。
一个事务中存在项的个数,我们通常将其定义为宽度。 一般若项集I 是事务tj的一个子集,那么我们通常称I 包含于tj。 我们仍然拿购物篮实例来举例,在上表二元表示中第三个事务中包含项集{啤酒,可乐},但不包括项集{鸡蛋,可乐}。
某个指定项集的事务的总个数我们将之称为支持度计数,是项集中的一个重要性质。 在后续算法中会经常用到。
(3)关联规则
若存在不相交的两个项集X,Y(即X∩Y=∅)且可以写成X—>Y 的蕴含式,关联规则就是这个蕴含式。 置信度和支持度定义式为:
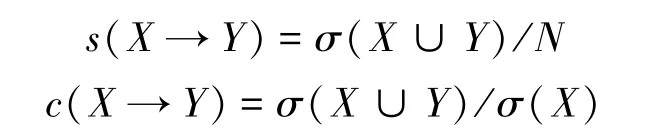
3.2 关联规则的挖掘过程
关联规则的挖掘过程问题我们通常可以有以下描述。 一般关联规则的算法都会采用把挖掘工作任务分成频繁项集的产生及规则的提取两个中心任务的方法策略。
规则具体的挖掘流程如图2 所示。
3.3 关联规则的分类
数据挖掘在早期主要集中研究关联规则的定义及算法设计[2],随着对关联规则的逐步研究,关联规则的形式多种多样,从关联规则的维度的角度,有以下四种分类方法[3-7]:
(1)布尔型关联规则与数值型关联规则
这两种类型的关联规则是依据处理的数据是什么类型决定的,数据类型的不同分成了布尔和数值两类。 如果关联规则是数值型的,我们不应该直接进行挖掘,而要依据实际情况转化成便于挖掘的新的数据形式。
(2)单层关联规则和多层关联规则
每一个数据集中的数据是处于不同抽象层次的,单层和多层是以此来划分的,所在不同的抽象层次有不同放入名称。 如图3 所示,其展示了不同的层次,长虹=>创维是在同一层次,这是一个单层规则。 彩电=>创维在不同层次。 这种规则称为多层关联规则。

图3 电视机层次图
(3)单维关联规则和多维关联规则
我们将关联规则分为单维关联规则和多维关联规则,依据的是规则前后数据项的维度不同。 当前后数据项都只包括唯一一个元素时,我们称之为单维关联规则。 如,长虹=>创维。 当前后数据项都包括多个元素时,我们称之为多维关联规则。如,梨,橘子=>西瓜,苹果。
(4)特殊型关联规则
当伴随条件出现在关联规则蕴含式的前半部分或后半部分时,我们称之为特殊关联规则。 如,¬ 苹果=>梨,表示如果用户不买苹果,他们更有可能买梨。
4 Apriori 算法
4.1 基本概念
Apriori 算法是Agrawal 和R.Srikant 于1994 年提出的,为布尔关联规则挖掘频繁项集的原创性算法[AS94b][8]。 Apriori 算法是第一个关联规则算法,是数据挖掘中常用算法[9-12],其原理是分为生成候选集和计算候选集支持度两步获得频繁项集。通过先验原理对未知进行判断分析。 相较于其他挖掘算法该算法应用领域比较广泛,商品的市场价格就可以通过Apriori 算法来合理的评估分析,在这个网络通讯飞速发展的时代,运营商也可以通过此算法挖掘客户用网习惯指导改进流量推送等,还可以通过对学生成绩的分析进行课业调整针对性的帮助学生。
4.2 Apriori 算法
4.2.1 性质定理
任意一个频繁项集的非空子集也是频繁的。在第二章中购物篮的实例中可得{面包,牛奶,尿布}显然是一个频繁项集,同时根据实例可得{面包},{牛奶}和{尿布}分别都为频繁项集,这样的结果与定理相符。 同理我们可以推出以下结论:不是频繁项集的超集同样也不是频繁项集。
4.2.2 算法特点
每一种算法都有各自的优缺点,其中Apriori算法的优点与其他算法相比比较明显,那就是算法简单易懂,思路清晰且易于实现。 但其也存在一些缺点,不太利于用在大数据集上面,因为当我们计算支持度计数时,需要对数据集中的所有记录全部进行扫描,这就需要相当大的I/O 负载。
4.2.3 算法思想
过程分为两个步骤:第一步通过迭代,检索出事务数据库中的所有频繁项集,即支持度不低于用户设定的阈值的项集;第二步利用频繁项集构造出满足用户最小信任度的规则。
具体做法就是:首先找出频繁1-项集,记为L1;然后利用L1 来产生候选项集C2,对C2 中的项进行判定挖掘出L2,即频繁2-项集;不断如此循环下去直到无法发现更多的频繁k-项集为止。 每挖掘一层Lk 就需要扫描整个数据库一遍。 通过性质定理我们知道,生成一个k-itemset 的候选项时,如果这个候选项有子集不在(k-1)-itemset(已经确定是frequent 的)中时,那么这个候选项就不用拿去和支持度判断了,直接删除。
具体而言:
(1)连接步
为找出Lk(所有的频繁k 项集的集合),通过将Lk-1(所有的频繁k-1 项集的集合)与自身连接产生候选k 项集的集合。 候选集合记作Ck。 设l1 和l2 是Lk-1 中的成员。 记li[j]表示li 中的第j 项。 假设Apriori 算法对事务或项集中的项按字典次序排序,即对于(k-1)项集li,li[1]
(2)剪枝步
Ck 是Lk 的超集,也就是说,Ck 的成员可能是也可能不是频繁的。 通过扫描所有的事务(交易),确定Ck 中每个候选的计数,判断是否小于最小支持度计数,如果不是,则认为该候选是频繁的。因此我们可以利用Apriori 性质定理来压缩Ck,如果某个候选的非空子集不是频繁的,那么该候选肯定不是频繁的,从而可以将其从Ck 中删除。
4.2.4 算法代码
以下是Apriori 算法的伪代码:
L1=find_frequent_1-itemsets(D); / / 找出所有频繁1 项集
For (k=2; Lk-1! =null; k++) {
Ck=apriori_gen(Lk-1);/ /产生候选,并剪枝
For each affair t in D{/ /扫描D 进行候选计数
Ct=subset(Ck, t); / / 得到t 的子集
For each 候选c 属于 Ct
c.count++;
}
Lk={c 属于Ck | c.count>=min_ sup}
}
Return L=所有的频繁集;
第一步:连接
Procedure apriori_gen (Lk-1: frequent (k-1)-itemsets)
For each 项集L1 属于Lk-1
For each 项集 L2 属于Lk-1
If((L1[1] =L2[1])&&( L1 [2] =L2 [2])&&……
&& (L1 [k-2]=L2 [k-2]) && (L1 [k-1]< L2 [k-1])) then {
c=L1 连接L2 / /连接步:产生候选
if has_infrequent_subset(c,Lk-1) then
delete c; / /剪枝步:删除非频繁候选
else add c to Ck;
}
Return Ck;
第二步:剪枝
Procedure has_ infrequent_ sub (c: candidate k-itemset; Lk-1: frequent (k-1)-itemsets)
For each (k-1)-subset s of c
If s 不属于 Lk-1 then
Return true;
Return false;
5 Apriori 算法在成绩中的应用分析
5.1 挖掘对象的确定
本文将截取部分学生期末成绩信息,并且将各科成绩合并为成绩的数据库文件用于之后的关联分析。 为了得到适合挖掘的信息,还需要对截取的数据信息进行整理。
5.2 预处理成绩数据
我们需要先将数据标准化,因为由上一节可知Apriori 算法只能应对布尔型变量,只有标准化后才能进一步快捷的分析成绩。 将每门课的分数都标准化处理,标准化的原则是将每门学科的分数与每门学科的总分数乘以0.85 所得的值进行比较。如果它不小于该值,则该分数将设置为1,否则将设置为0。
5.3 数据集成
截取学生期末成绩如表2 所示。

表2 学生成绩
用I1、I2、I3、I4、I5分别表示数据结构、C 程序设计、计算机基础、数据库原理、数据挖掘5 个学科。学生成绩经过处理后,如表3 所示。
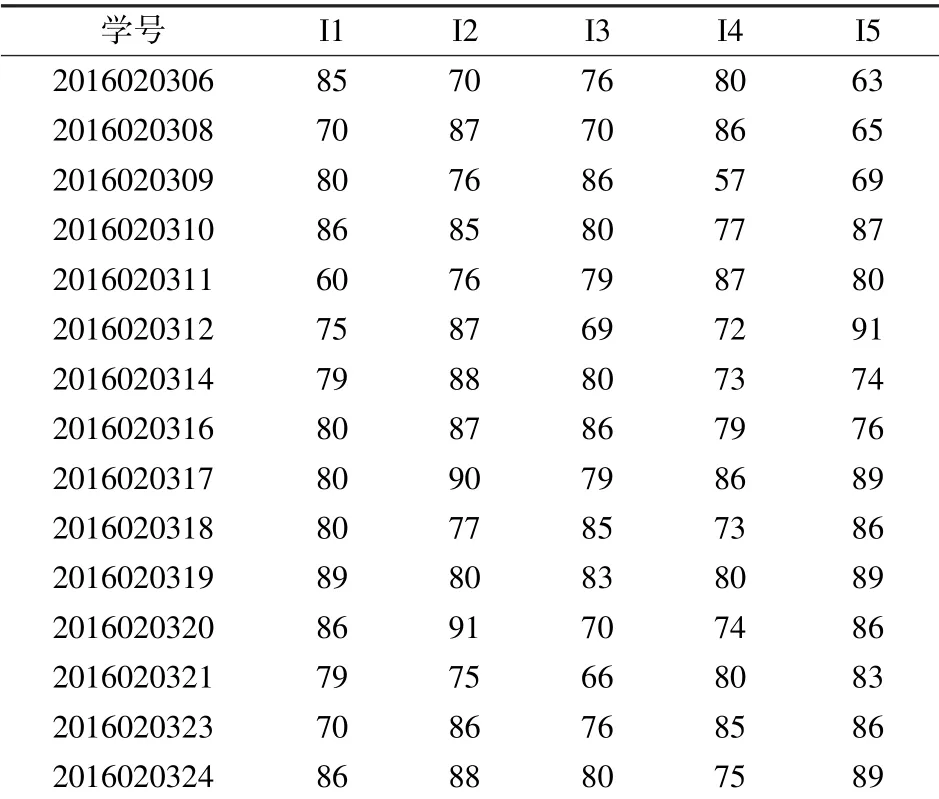
表3 处理后学生成绩
5.4 频繁项集产生
以上面截取成绩为例,首先利用算法找到频繁项集。 根据实际情况我们将支持度计数定为3,这样通过上面介绍的计算方法得出的最小支持度是20%。 根据理论要求先生成第一候选项集C1,与指定的最小支持度3 进行比较,无需剪枝就能满足频繁的需求。 第二步通过自连接的方法生成第二候选项集C2。 最终产生频繁项集为{I1,I2,I5}。
5.5 置信度的计算
L={I1,I2,I5}为频繁项集,其中{I1,I2,I5},{I1,I2},{I1,I5},{I2,I5},{I1},{I2},{I5}均为L的子集。 下面为置信度的计算:
I1→I2∧I5,置信度=3/6=50.0%
I2→I1∧I5,置信度=3/4=75.0%
I5→I1∧I2,置信度=3/4=75.0%
I1∧I2→I5,置信度=3/9=33.3%
I1∧I5→I2,置信度=3/9=33.3%
I2∧I5→I1,置信度=3/6=50.0%
5.6 成绩分析
由以上算出的非空子集置信度的结果分析可得以下结论:
(1)若I1优秀,则I2、I5优秀可能性达50%以上
(2)若I2优秀,则I1、I5优秀可能性达75%以上
(3)若I5优秀,则I1、I2优秀可能性达75%以上
(4)若I1、I2优秀,则I5优秀可能性达33.3%以上
(5)若I1、I5优秀,则I2优秀可能性达33.3%以上
(6)若I5、I2优秀,则I1优秀可能性达50%以上
由(1)-(6)分析学生成绩得:
当某学生数据结构和C 程序设计同时优秀时,数据挖掘优秀的可能性达33.3%以上;当其数据结构和数据挖掘成绩优秀时,C 程序设计优秀的可能性达33.3%以上;当C 程序设计和数据挖掘优秀时,数据结构则有50%以上优秀可能性,即学生在学完C 程序设计和数据挖掘后,数据结构的成绩会更加优秀;学生在数据结构优秀的同时,C程序设计和数据挖掘同时优秀的可能性只有50%,所以不应该先开数据结构这门课程。 由以上分析得,学院可以通过关联规则分析结果来安合理调整课顺序,从而达到提高教学效率的目的。
5.7 代码实现及运行结果
算法实现及结果如图4~图7 所示。
6 结语
图4

图5
本文主要将Apriori 算法应用于学生实际成绩的分析,算法成功分析出各学科成绩之间的关联联系,分析了算法的优缺点,但是在得知其缺点后,并没有进一步研究改进算法,解决Apriori 算法重复扫描导致工作量大的问题。 目前仅仅研究了通过学生成绩得出学科关联的问题,还有在其他方面比如通过关联规则分析个人,从而进行成绩预警等问题。 我们要对采集上的信息进行全方位、多层次的挖掘分析,从各个方面入手提高学生成绩。
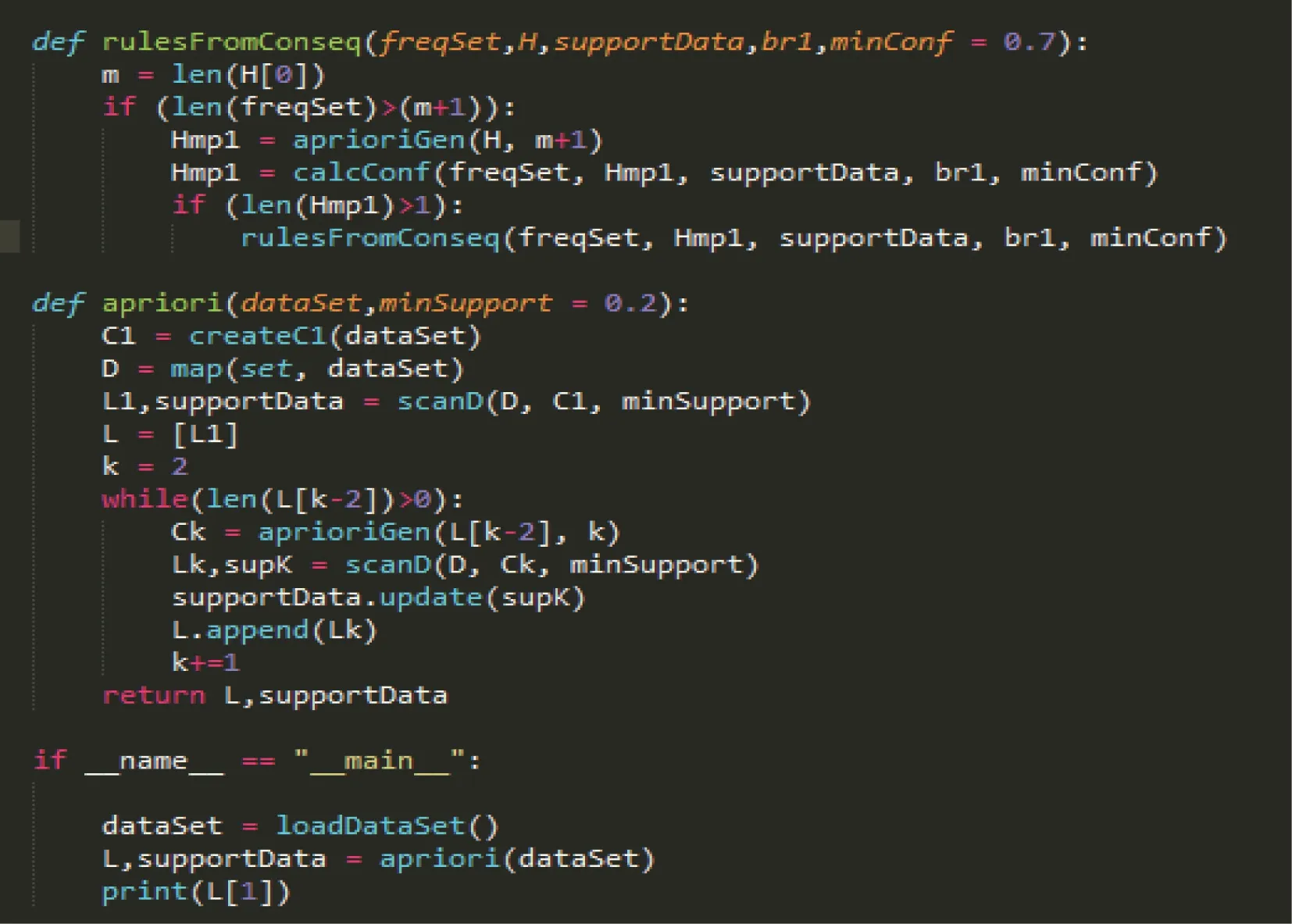
图6
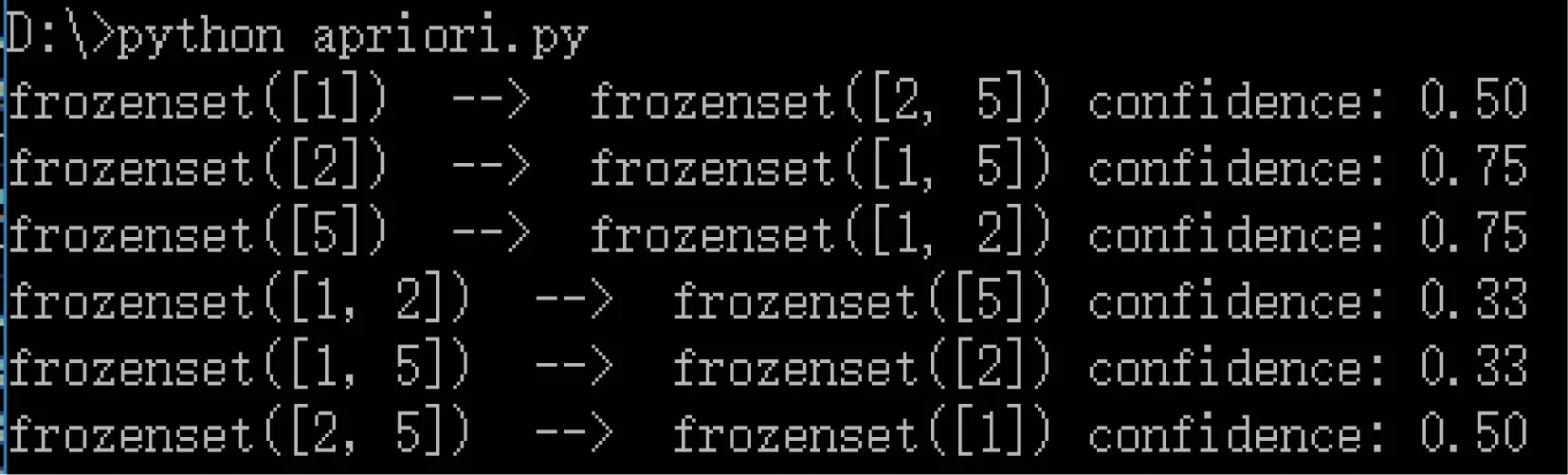
图7
