高速铣床主轴⁃轴承的振动特性分析

董 赫，朱向哲，陈 立

（辽宁石油化工大学机械工程学院，辽宁抚顺113001）

高速机床设备和工艺技术的发展，推进了高速切削、高效加工和高精制造等先进制造业技术的发展，采用主轴电动机与机床主轴合二为一的数控机床电主轴应运而生，它使主轴单元向高速、高效、高精度加工迈出了可喜的一步。目前，在以铣床为主的数控加工机床中，每分钟数万转的高速主轴已被广泛利用，更有高达1 000 000 r/min以上乃至更高转速的高速主轴[1⁃4]。超高速主轴产品装备带动了数控机床的高速化，同时由于工作中机动载荷复杂，且主轴上不可避免地存在较小的不平衡量，使主轴产生振动从而导致主轴发生变形，易造成轴承发生破坏。因此，电主轴是研究数控机床可靠性的重要环节。

铣床在加工时现场发生的不平衡故障占主轴振动故障的80%以上，其原因之一是主轴不可避免地存在不平衡量，主轴产生强烈振动，当外力作用频率与主轴的固有频率相同或相近时激发共振。振动影响机床的精度和主轴的使用寿命[5⁃6]，从而导致主轴结构产生疲劳破坏。主轴是铣床的核心部件，其中滑动轴承具有损耗低、寿命长和承载高等优点，因此研究以滑动轴承为支撑的主轴振动的规律，有效抑制或减小高速主轴的不平衡振动，成为研究铣床主轴动态特性的重要内容。

本文以德国GMN某型高速铣床电主轴为例，采用有限元方法，建立了主轴⁃轴承系统的有限元模型，研究了主轴的固有振动特性，分析了轴承刚度对主轴固有频率和临界转速的影响。在此基础上，研究了高速主轴的不平衡响应特性，分析了不平衡量大小和位置等因素对主轴振动敏感度的影响规律，利用支承刚度和不平衡量的曲线变化来表征转速及振幅对主轴稳定性影响，以期为高速机床主轴系统的动力学设计提供一定的理论依据。

1 铣床主轴的有限元模型

以德国GMN公司设计的某型高速铣床电主轴为研究对象。该电主轴额定转速为60 000.00 r/min，最高转速可达120 000.00 r/min，最大输出功率为1.1 kW。高速铣床电主轴的有限元模型如图1所示。

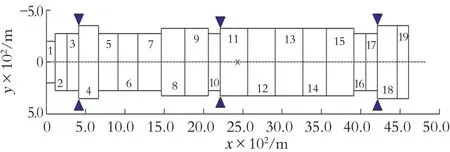
图1 高速铣床电主轴有限元模型

该主轴的总长度为461 mm。考虑高速主轴的离心力和陀螺力矩效应，利用Timoshenko梁单元建立主轴、轴承等部件的有限元模型，模型共分为20个节点，19个单元。主轴材质密度ρ=7 850 kg/m3，弹性模量E=2.06×1011Pa，泊松比v=0.3。主轴的节点4、11、18为轴承支承位置，其刚度均为1×108N/m。

2 临界转速和振型

临界转速是主轴的“共振点”，当主轴在升速过程中经过临界转速时如果不进行恰当的处理，则会因主轴的振动幅度过大而造成主轴结构的损坏。精确计算临界转速和振型是为了便于系统的调整，减小逾越临界转速过程当中产生的振动[7⁃8]。主轴前3阶临界转速随轴承刚度的变化曲线如图2所示。从图2可以看出，当主轴的轴承刚度按数量级递增时，相同一阶的临界频率会随主轴的轴承刚度增大呈非线性增大；高速铣床主轴的前2阶临界转速对轴承刚度的变化更加敏感。

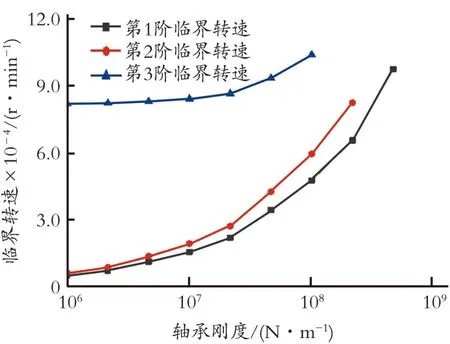
图2 主轴前3阶临界转速随轴承刚度的变化曲线

临界转速因轴承刚度的变化而发生变化的同时，相应的主轴振型也随之产生变化。主轴前3阶的临界转速和振型随轴承刚度的变化见表1。

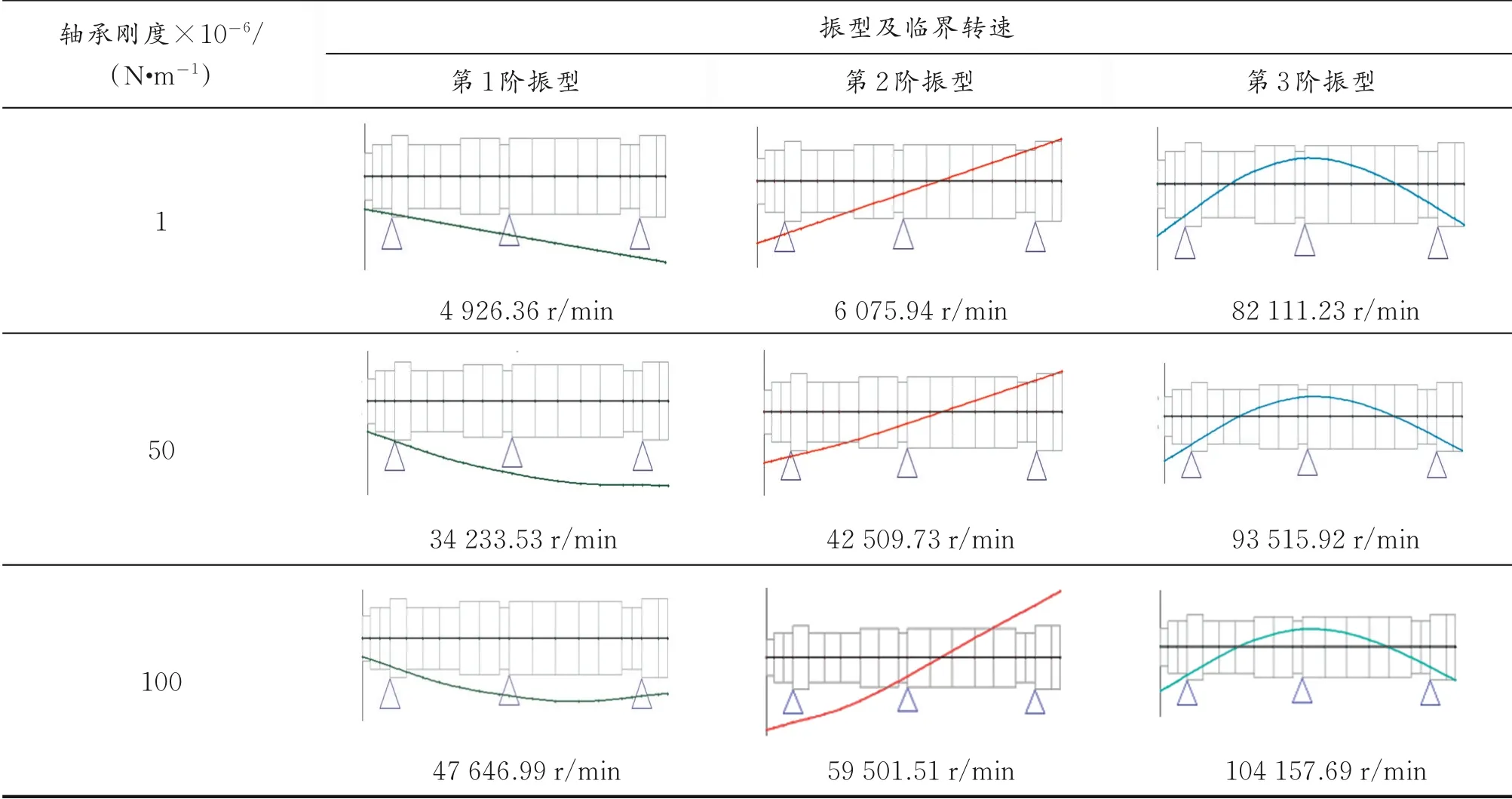
表1 主轴前3阶的临界转速和振型随轴承刚度的变化

观察表1发现，高速铣床主轴的轴承刚度影响主轴的临界转速和振型；随着轴承刚度的逐渐增加，主轴前3阶临界转速逐渐增大；轴承刚度对主轴振型也具有较大的影响。当轴承刚度为1×106N/m时，主轴的前2阶振型均为刚体模态振型；当轴承刚度增加到5×107N/m时，主轴的前2阶振型转变为弹性模态振型。因此，在工程实际中，合理地选择铣床主轴的轴承刚度具有重要意义。

3 不平衡响应分析

当主轴存在材质不均匀、加工误差、装配误差以及机床运行不当等情况时，在实际工作中会出现质量偏心的情况，这种质量偏心在现实中也是很难消除的。因此，分析不平衡响应的目的是使机械运行的振幅控制在允许的范围内，尽量减少对机床其他部分的损坏，维持设备的正常运行。当铣床正常工作时，受到一定载荷的动力响应是不可避免的，主轴在微小的不平衡力作用下所产生的振动称为不平衡响应[9⁃10]。若要得到主轴不平衡量的振动特性，则需要知道铣床主轴不平衡量的大小及其分布位置，但是对大多数铣床主轴来说，这些量往往都是未知量。因此，通过计算所得的主轴不平衡响应确定主轴不平衡量位置的敏感度，或在不平衡量已知的情况下计算不平衡响应，确定工作转速下主轴的振动规律。

3.1 不平衡量的计算

根据有限元理论，运用Lagrange方程，得到不平衡响应有限元方程[11]：

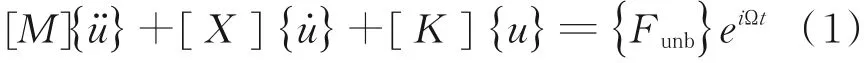
式中，[M]、[X]、[K]分别为质量矩阵、阻尼矩阵、刚度矩阵；{ü}为加速度矢量，m/s2；{u̇}为速度矢量，m/s；{u}为位移矢量，m；{Funb}为不平衡力矢量，N；Ω为旋转角频率，rad/s；e为偏心距，mm；t为时间，s。

式（1）直接采用积分Newmark法进行求解[12]：

式中，α、β为参数，本文取α=1/6，β=1/2。

3.2 不平衡响应分析

3.2.1 不同转速下的振幅 转速的变化范围为0～120 000.00 r/min，不平衡量保持不变，其大小为0.000 30 kg·m，不平衡量施加于节点11上，对主轴进行不平衡响应分析。节点11上不平衡量施加示意图如图3所示。

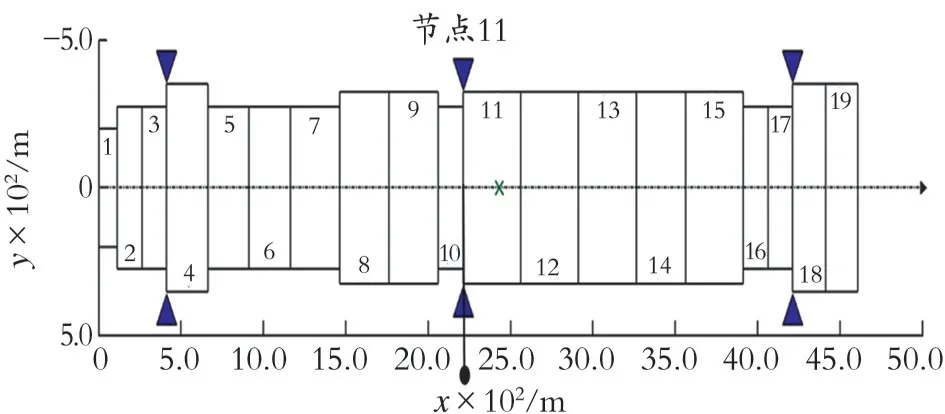
图3 节点11上不平衡量施加示意图（不平衡量：0.000 30 kg·m）

主轴各节点不平衡响应曲线如图4所示。由图4可以看出，主轴各节点的不平衡响应曲线中存在3个峰值，转速为48 840.00 r/min时对应第一个峰值，转速为59 100.00 r/min时对应第二个峰值，转速为104 700.00 r/min时对应第三个峰值，对应于整个主轴系统的第1阶、第2阶和第3阶的临界转速分别为47 646.99、59 501.51、104 157.69 r/min。尤其是，在0～120 000.00 r/min，该主轴系统对第3阶临界转速的敏感度大于第1阶和第2阶的临界转速。因此，当主轴处于这3个峰值转速附近时，可能会产生共振。由于该主轴的额定转速较高，故在机床开机启动的过程中尽量使主轴加速通过这几个速度范围，减小发生共振峰的时间，从而避免铣床主轴发生剧烈震动的时间过长，提高使用寿命。

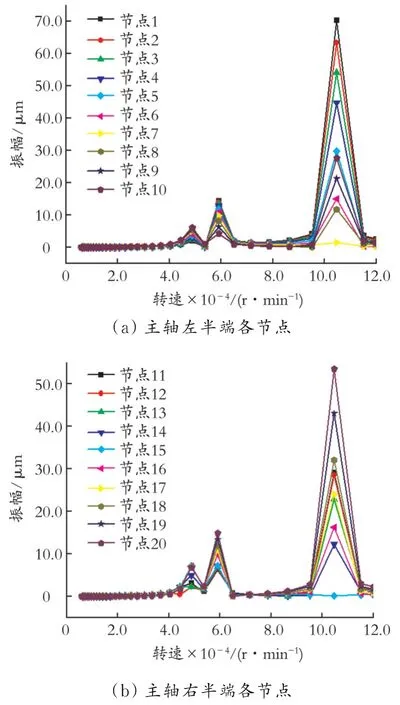
图4 主轴各节点不平衡响应曲线

由图4还可以看出，当主轴存在不平衡量，且主轴转速接近临界转速附近时，主轴位移响应会急剧增大，引发共振，共振可能会导致如下几种情况：（1）导致主轴结构产生损坏，影响使用寿命；（2）带动工件与机床产生相对的振动，降低加工表面精度，影响使用性能或磨削截面、磨削角度的现象随之变化，磨损刀具造成加工无法继续进行；（3）造成机组运转不稳定，导致机床出现故障，影响机组的运行安全。

3.2.2 不平衡量位置对主轴振动的影响 设定主轴的工作转速为60 000.00 r/min，主轴的不平衡量大小为0.000 30 kg·m，分别位于节点4、11、15、18，研究不平衡量位置对主轴各节点振幅的影响。

工作转速下不平衡量位置对主轴各节点振幅的影响见图5。由图5可知，在高工作转速下，当同一不平衡量分别施加于节点4、11、15、18时，主轴两端的振幅均大于主轴中间部分的振幅；无论不平衡量施加在哪个节点上，主轴前半部分的振幅都逐渐减小，约在节点11到节点14附近的轴段处主轴的幅值最小；从节点14后的节点开始，振幅的变化情况与节点10前的振幅变化相反。若不平衡量存在于主轴两端，则主轴不平衡响应的振幅相对较大。

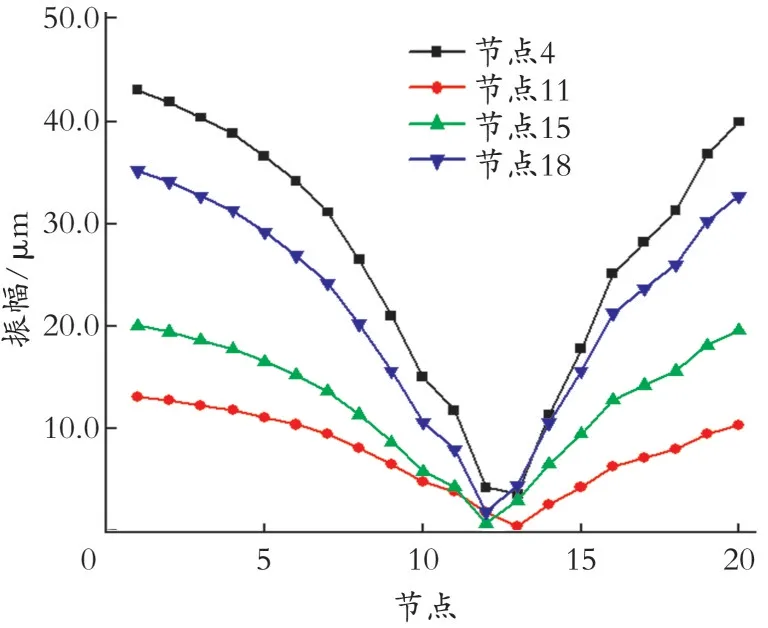
图5 工作转速下不平衡量位置对主轴各节点振幅的影响

不平衡量施加于不同节点时主轴的最大振幅及最大振幅位置见表2。

表2 不平衡量施加于不同节点时主轴最大振幅

由表2可知，当不平衡量施加于节点4时，主轴两端产生了最大振幅，振动响应明显，其最大振幅约为最小振幅的10倍（由图5可知，不平衡量施加于节点4时的最小振幅约为4μm）；不平衡量施加在节点18时，主轴的最大振幅小于不平衡量施加在节点4时的最大振幅，最大振幅相差7.87μm；不平衡量施加在节点15时，最大振幅约为不平衡量施加在节点4时最大振幅的1/2；不平衡量施加在节点11时最大振幅最小。由此可知，不平衡量施加在节点4和节点18，主轴两端振动响应最为敏感。

3.2.3 不平衡量大小对主轴振动的影响 设铣床主轴的转速为60 000.00 r/min，将不平衡量以0.000 05 kg·m为单位逐渐增加，分别施加于节点4、11、18处，研究主轴节点1、6、13、20处不平衡量大小对主轴振动的影响。工作转速下不平衡量施加在不同节点时其大小对主轴不同节点振幅的影响见图6。

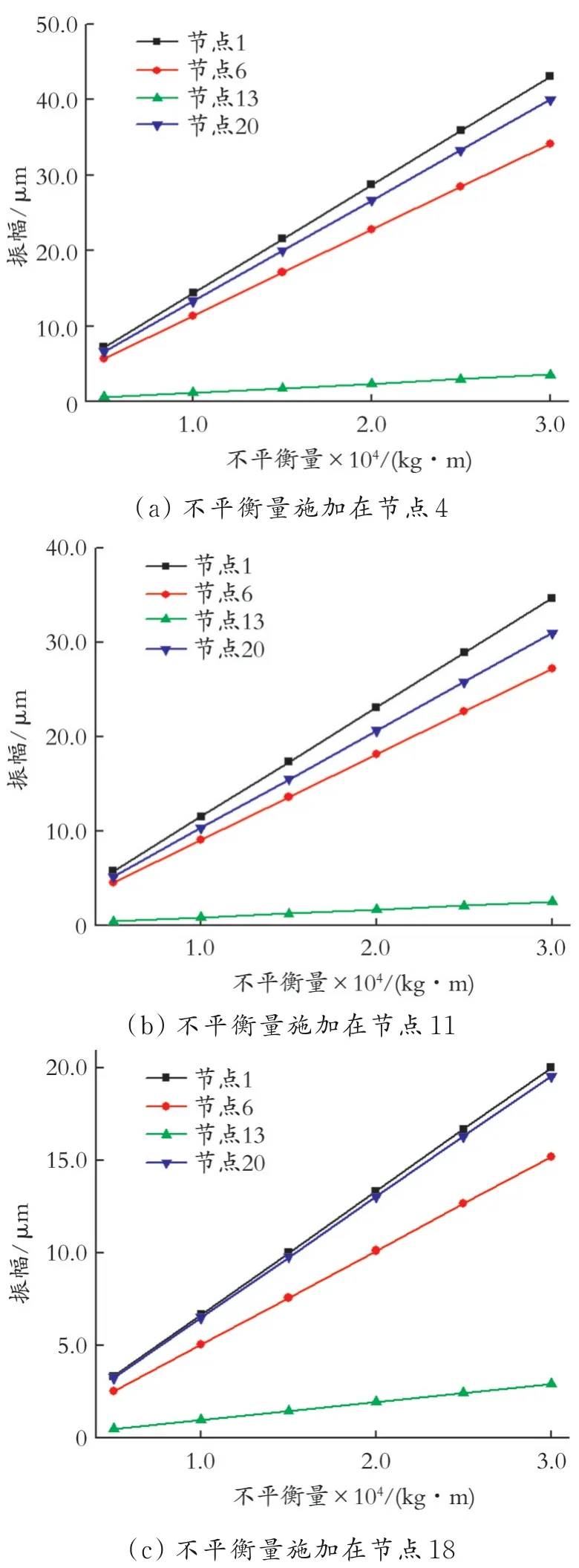
图6 工作转速下不平衡量施加在不同节点时其大小对主轴不同节点振幅的影响

由图6可知，主轴在同一转速下，不平衡量从0.000 05 kg·m增加到0.000 30 kg·m时，节点1、6、13、20处相应的振幅变化趋势皆为逐渐增大。综合来看，主轴的振幅随着不平衡量的增加而变大，但是其斜率变化情况大不相同。当施加在节点4上的不平衡量发生变化时，节点1、6、13和20的振幅变化最大；当施加在节点11上的不平衡量发生变化时，节点1、6、13和20的振幅变化次之；当施加在节点18上的不平衡量发生变化时，节点1、6、13和20的振幅变化最小。由图6还可以看出，节点1、6和20对不平衡量的施加位置更加敏感，而节点13对不平衡量施加的位置反馈有微小的变化，再次印证了主轴节点10前和节点14后对不平衡量存在较大的敏感度，而中间轴段对不平衡响应的敏感性相对较弱。综上，随着不平衡量的增大，相应的振幅也随之增大，但是施加位置不同时，不同节点振幅的变化也不尽相同。

4 结 论

（1）铣床主轴的各阶临界转速随着轴承刚度的增大呈非线性增加，振型也随之发生明显的变化。随着轴承刚度增加，主轴的前2阶振型均由刚体模态振型转变为弹性模态振型。因此，合理地选择铣床主轴的轴承刚度，一定程度上可以有效控制主轴的振动特性。

（2）铣床主轴因材质的不均匀、加工偏差、装配偏差以及机床运行不当等原因存在不平衡量时，主轴会产生振动。在0～120 000.00 r/min，主轴各节点的不平衡响应曲线存在3个峰值，对应于整个主轴系统的前3阶的临界转速。尤其是，该主轴系统对第3阶临界转速的敏感度相对较大。

（3）铣床主轴振幅随着不平衡量的增加而增大，但是不同节点对不平衡量位置的振动其敏感度并不相同。当不平衡量位于主轴的轴承位置附近时，主轴两端振动响应最为敏感；主轴中间段对不平衡量位置的敏感度相对较弱。因此，对主轴两端，特别是主轴和刀具的结合段，应当合理控制振幅，提高铣床的加工精度。