求解抛物型方程的两层高精度差分格式

陈佳欣，李旭生

（辽宁石油化工大学理学院，辽宁抚顺113001）

抛物型方程常常应用于扩散、热传导等领域，而且应用的范围很广，研究方向也比较多[1⁃2]。学者们对抛物型方程进行了大量分析，进而丰富了抛物型方程理论，也加深了抛物型方程与其他自然学科领域的联系，但是抛物型方程形式复杂，解析形式的解很难求出，所以讨论方程的数值解法十分有意义。随着对抛物型方程研究的不断深入，对抛物型方程数值解法的研究也越来越广泛，通常要面临如何解决实际问题，提出一个好的方法显得尤为重要。在构建不同的差分方程过程中，主要的目的是得到一个具有高精度的截断误差且结果更为精确和稳定的差分格式。就目前来说，构造差分格式的方法有很多种，如有限差分法、有限元法、有限体积法、谱方法、pade逼近法等[3⁃4]。最常用的是有限差分法，这种方法的基本思想是将连续的问题离散化，对求解的区间用网格进行剖分，然后将微分算子离散化，从而把微分方程的定解问题转化为线性代数方程的求解问题[5]。

姜蕴芝等[6]根据Saul′ev算法对古典隐格式进行了一定改进，得到求解一维抛物方程的新格式，一种无条件且稳定的半隐格式，该格式的截断误差为并从半隐格式出发构造出一组显格式。半隐格式的稳定性与Saul′ev算法的稳定性相近，显格式的差分格式精度要高于Saul′ev算法。吐克孜·艾肯等[7]用C⁃N算法将偏微分方程转化为常微分方程组，通过使用指数函数的Trotter积分公式将该方程组系数矩阵分块成多个小矩阵，并通过C⁃N算法求得结果。该方法计算量少且恒稳定。张莉等[8]基于组合差商法提出一个绝对稳定的隐式格式，并将空间上的6个点进行taylor展开，使其达到一定精度。曾文平[9]构造一组3层高精度的双参数隐式差分格式，当参数α=0.5、β=0时，得到一个2层格式，当参数为非负数时，该格式是绝对稳定的，其截断误差在空间和时间步长上的精度分别为6阶精度和2阶精度。W.R.Hao等[10]通过区域分裂的方法得到一个求解抛物型方程的高精度显式格式，该格式的截断误差为O(τ3+h3)。詹涌强等[11]通过使用待定系数法构造一个求解抛物方程的高精度隐式算法，该隐式差分格式的截断误差为O(τ3+h4),当r＞时，该差分格式是稳定的。周敏等[12]首先进行网格剖分，然后选取线性无关的节点，利用这些节点构造出一个含有多个参数的差分格式，并对该格式的某一点进行泰勒展开，使用待定系数法使截断误差达到一定的精度，然后求解参数。得到一个2层8个点的隐式差分格式，此格式的截断误差为O(τ3+h5)，在0.001＜r＜0.231或0.236＜r＜0.772具有稳定性。M.S.Ma等[13]构造了一个时间步长和空间步长均为4阶的高精度隐式格式，该隐格式的稳定性条件为0＜r≤1。文献[14]构造出一个求解抛物型方程的3层高精度隐式格式，数值算例证明了格式的精确性和可行性。

本文利用待定系数法和泰勒展开法构造出新的隐式差分格式，该差分格式精度为时间上的3阶精度，空间上的5阶精度，比文献[8—11]精度高，该格式数值解比文献[12—13]的数值解更接近精确解，文献[14]的精确性与本文精确性相当，但是文献[14]的算法为3层差分格式，3层差分格式在迭代计算时不是自启动的。提出的差分格式为2层格式，相比3层差分格式，在保持较好的精度的同时，差分格式也较为简单，然后对格式的稳定性进行了理论分析，最后得出一系列数值解验证此格式的可行性。

1 差分格式的构造

考虑如下抛物型方程的初边值问题：

式中，L为空间长度；T为时间长度；u(x,0)为初始值；u(0,t)、u(L,t)为边界值；a为正常数。

首先选取空间步长为h=LK，然后选取时间步长为τ=TM，其中K、M都是正整数，然后用两簇平行线将矩形区域分割成矩形网格，再用适当的差商代替方程中相应的偏微商，从而求得所要的差分格式。

对[0,L]×[0,T]这个矩形区域进行网格剖分，在网格点上选取局部节点集,(xj+1,tk+1),(xj-1,tk),(xj,tk)(xj+1,tk)，其中xj=jh,tk=kτ。将6个节点的u值点分别在节点（xj,tk）进行泰勒展开，得：

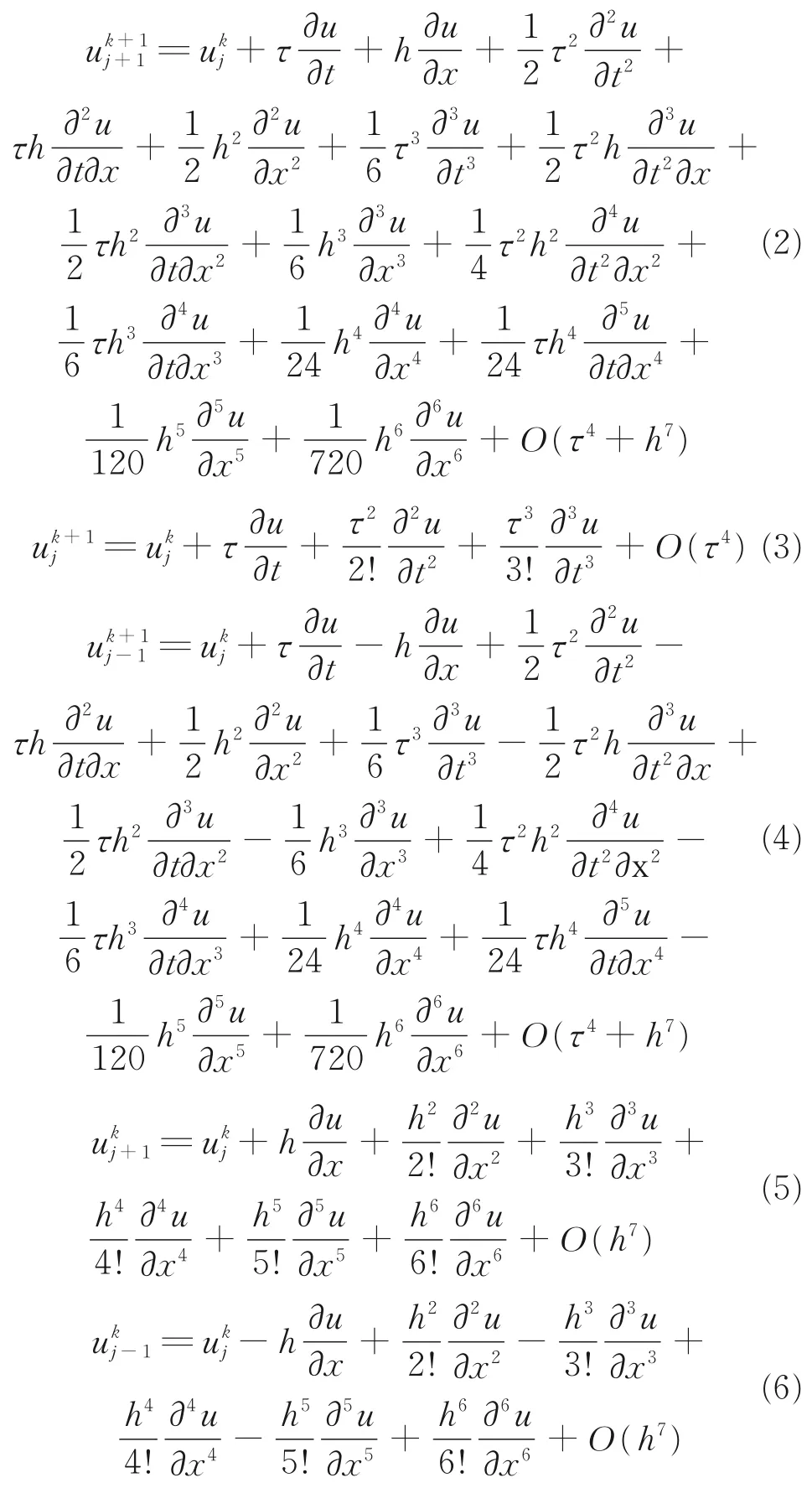
式中，ukj=u(xj,tk)。

然后分别求出差商的渐近表达式，其中Δtunj=：

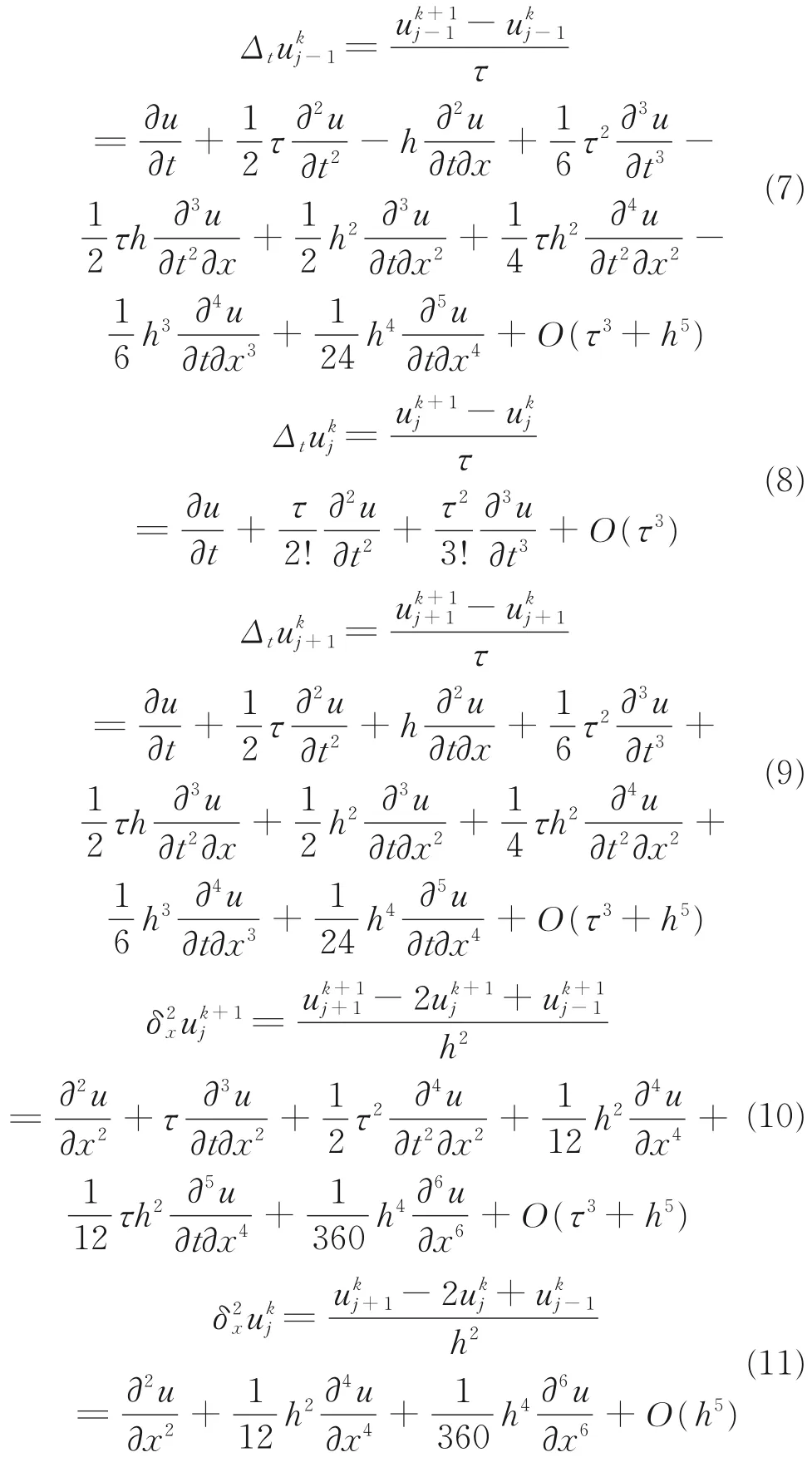
当问题(1)的解是充分光滑且连续时，通过aτ=h2r得：

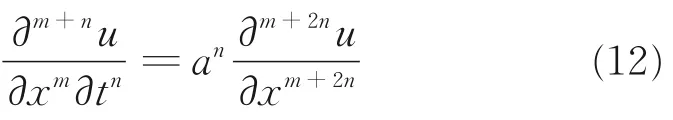
使用式(12)整理得：

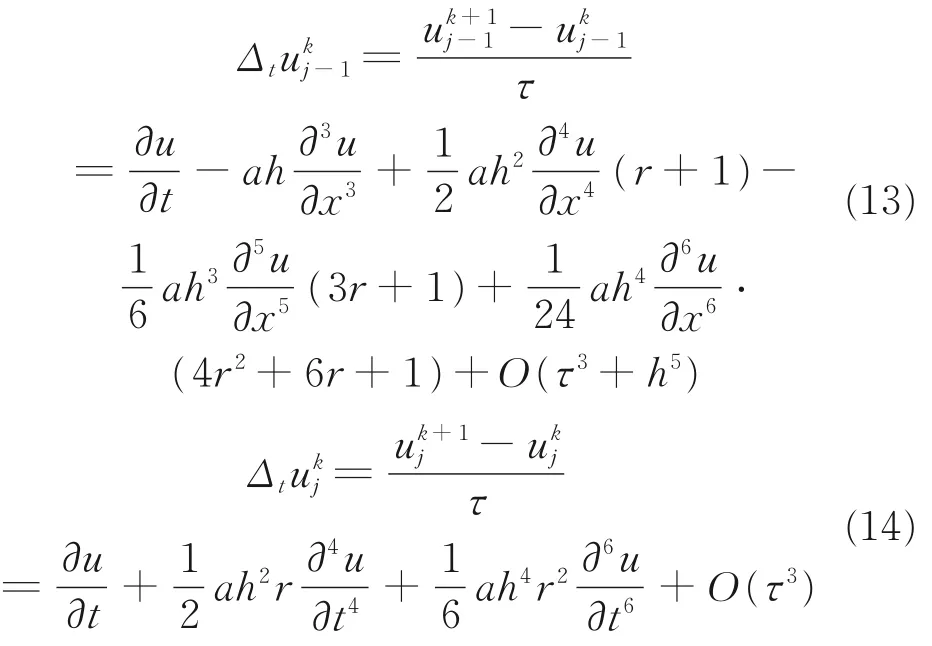
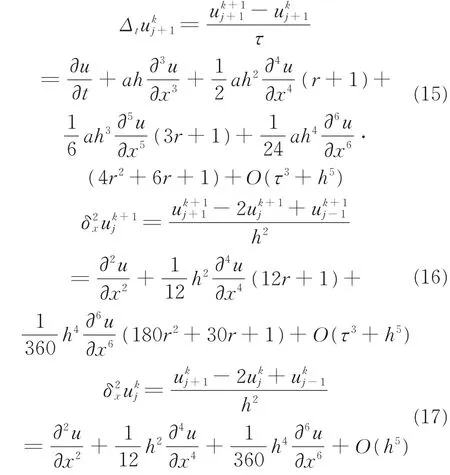
利用所求得的差商建立一个含有多个未知参数的差分算子：

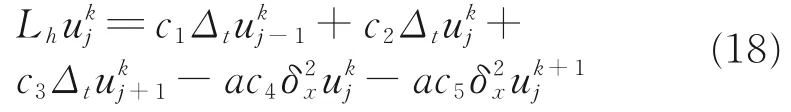
式中，ci为未知参数。

目的是用来逼近本文求解的微分算子：

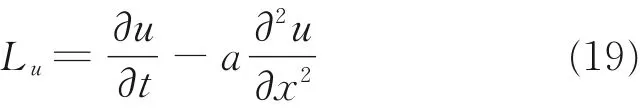
而在本文中所建立的差分格式中的未知数c1、c2、c3、c4、c5，即本文需要求解的系数。

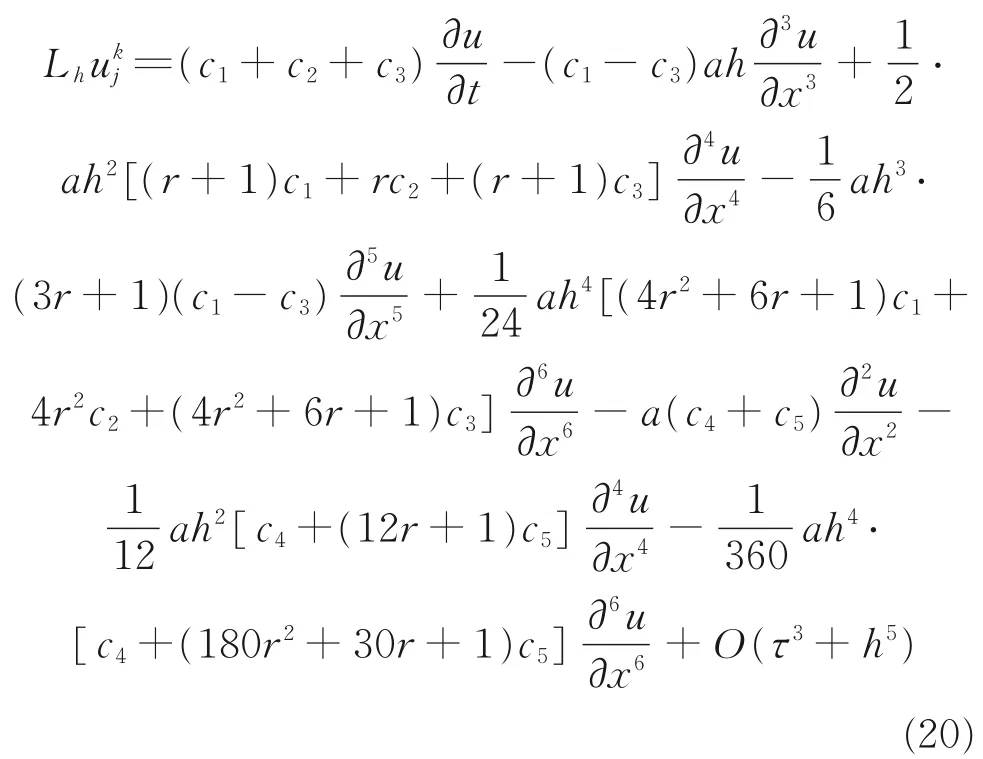
为了使式(20)差分格式的截断误差精度达到O(τ3+h5)，则需要满足：

求解各个系数分别为：

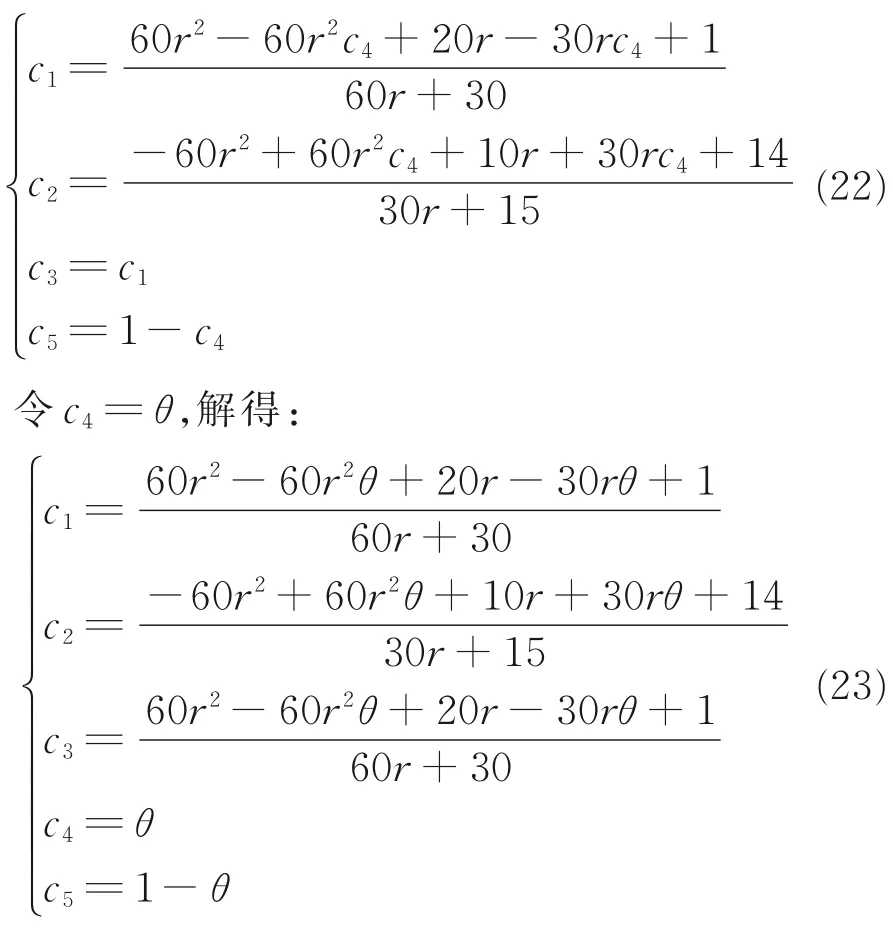
将c1、c2、c3、c4、c5分别代入差分算子中求得差分格式为：

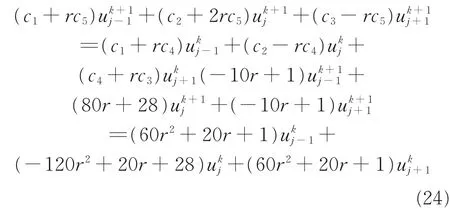
2 稳定性和收敛性

令差分格式中的系数分别对应A、B、C、D、E、F。

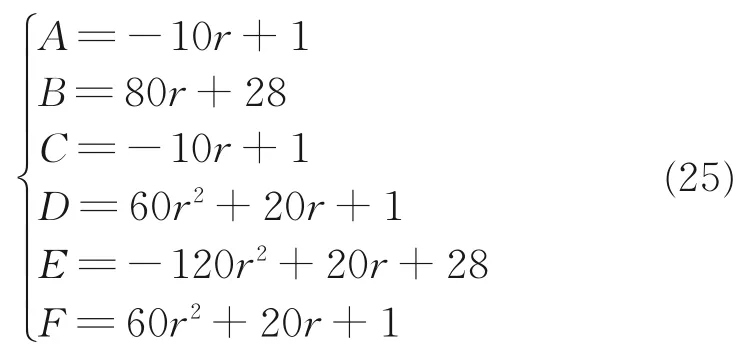
再利用Fourier分析法将差分格式化为矩阵形式，通过令ukj=vkeijθ进而可以将差分格式转化为矩阵的形式。

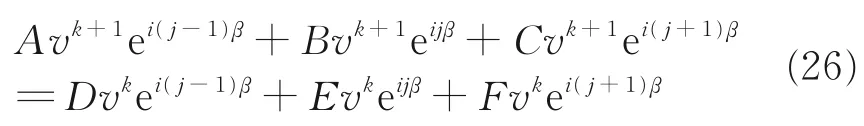
通过对矩阵进行消元，其目的是消去eijβ，得到新的格式为：

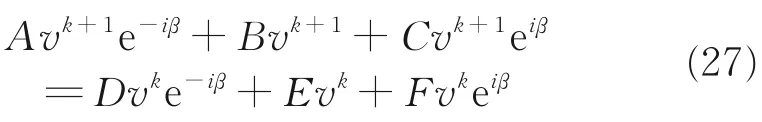
然后分别将A、B、C、D、E、F代入式(28)得：

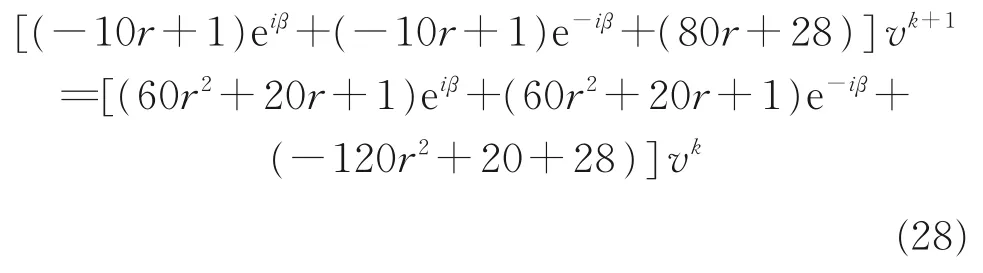
通过计算得出所需要的增长因子为：

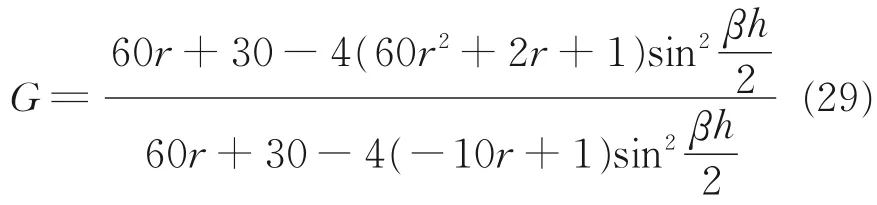
为了保证建立的差分格式的稳定性，则需满足|G|≤1的充分条件为：

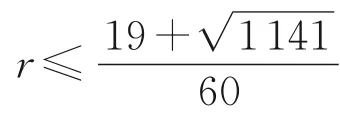
3 数值算例

考虑抛物型方程中一维常系数扩散方程为：

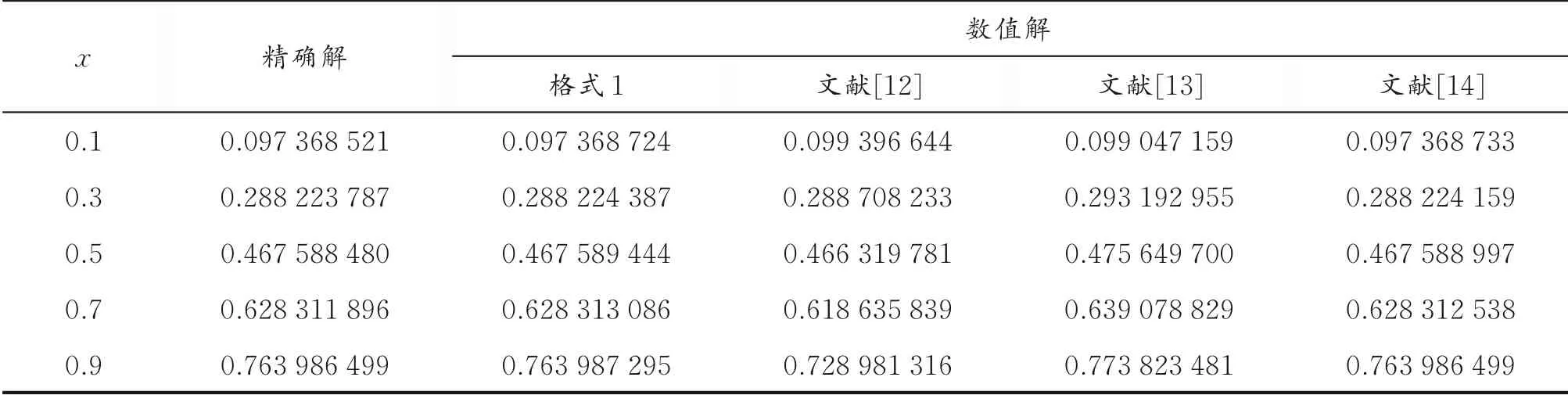
表1 当r=0.1、n=100时不同格式的数值解

表2 格式1数值解与精确解的比较结果

4 结 论

通过待定系数法构造出一个求解抛物型方程的两层差分格式，格式的截断误差为O(τ3+h5)，并对格式的稳定性进行分析，即，该格式是稳定的。从表1可以看出，文献[12—13]的绝对误差比格式1绝对误差大4个数量级，文献[14]与格式1精确性相当，但是文献[14]为3层差分格式。从表2可以看出，格式1数值解与精确解基本吻合，此格式具有精确性和可行性。