考虑二阶效应的混凝土桥墩弹塑性承载力理论研究与试验分析

2021-03-14兰树伟陈旭周东华毛德均王春华

铁道建筑 2021年11期

兰树伟陈旭周东华毛德均王春华

1.昆明学院建筑工程学院，昆明 650214；2.昆明理工大学建筑工程学院，昆明 650500

在水平荷载（如地震荷载、风荷载等）的作用下桥墩发生侧移，桥墩的侧向变形使得竖向荷载的作用点发生移动，由此会产生附加内力和附加变形，称为桥墩的二阶效应。高墩桥梁在公路和铁路工程中广泛应用，高墩由于其抗侧刚度相对较小，二阶效应明显。目前，高墩桥梁的二阶效应主要采用有限元软件进行计算，而工程师对隐含在软件内部的计算理论和方法了解较少，如何检验有限元计算结果是不可回避的问题。JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》［1］（以下简称规范）中给出了考虑二阶效应钢筋混凝土矩形截面弹塑性承载力的计算公式，规定混凝土受压区边缘应变始终取-0.33%，而轴心受压时的极限应变取-0.20%。规范不能运用整个混凝土本构关系曲线，造成应变从压弯到轴压的受力状态不连续，而多数承载力计算方法［2-5］都没有很好地解决该问题。规范主要是基于等效矩形应力图进行承载力计算的，这种计算方法存在一定的误差［6-8］。另外，规范中计算偏心受压构件时须先判别截面是大偏心受压还是小偏心受压，再选择相应公式进行计算，计算过程繁琐。

本文通过分析极限承载力状态的应变变化区域，以截面应变为自变量，利用混凝土和钢筋的本构关系确定应力，然后在截面上进行积分确定内力，得到考虑二阶效应的矩形截面配筋诺模图，并通过钢筋混凝土偏心受压柱试验验证其正确性。

1 计算方法与公式推导

1.1 本构关系

混凝土采用抛物线加矩形的应力-应变关系，忽略抗拉强度，其应力σc与应变εc关系式［9］为

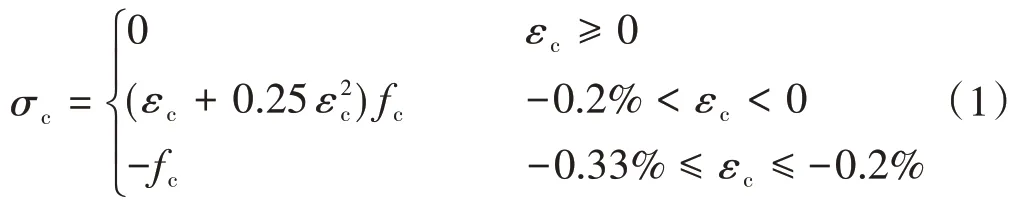
钢筋采用理想弹塑性模型，其应力σs与应变εs关系式为

式中：εy和Es分别为钢筋的屈服应变和弹性模量，εy=fy∕Es；fc为混凝土抗压强度设计值。

1.2 截面应变状态分区

规范中规定混凝土和钢筋的极限应变分别为-0.33%和1%，通过分析截面应变变化，以所有可能的应变构建应变状态分区（图1），每个区域确保截面一边（混凝土受压侧边缘或受拉钢筋）处于极限应变状态，可实现混凝土应变的连续过渡，将复杂的应变变化转化为仅求解一个未知量的问题。图中：b和h分别为截面的宽度和高度；h0为截面有效高度；As和A′s分别为受拉钢筋和受压钢筋面积；as和a′s分别为受拉钢筋合力点至截面受拉边缘的距离和受压钢筋合力点至截面受压边缘的距离；εc1和εs1分别为截面上边缘混凝土和钢筋的应变；εc2和εs2分别为截面下边缘混凝土和钢筋的应变。

图1 截面应变状态分区

不同截面应变变化规律和受力情况见表1。

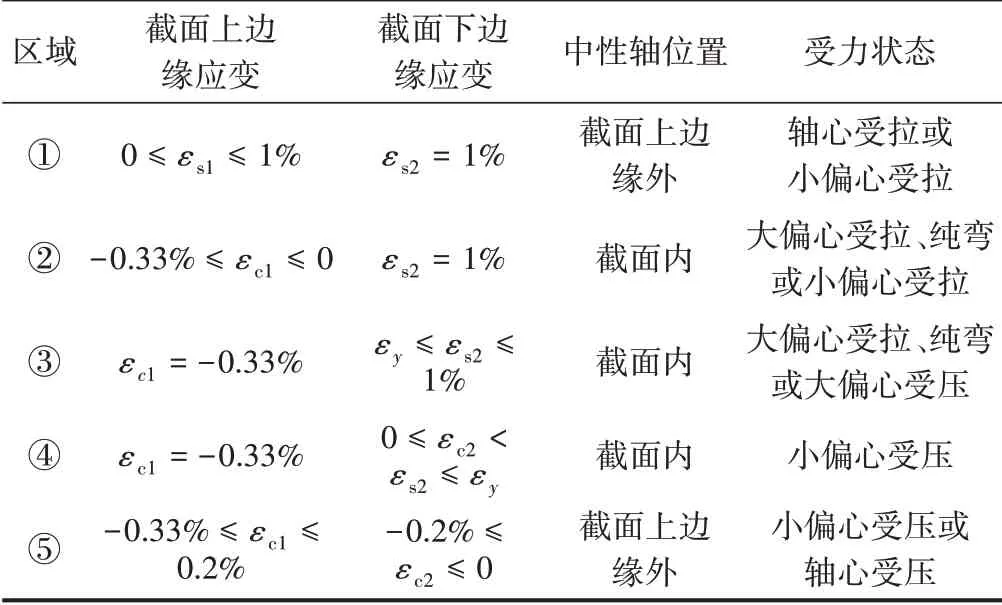
表1 不同截面应变变化规律和受力情况

由表1可知，区域①为轴心受拉或小偏心受拉，属于受拉状态，不考虑二阶效应。区域②和区域⑤混凝土的压应变是变化的，规范规定混凝土受压区边缘应变始终取-0.33%，因此规范公式不适用于这两个区域。区域⑤为构件受力从小偏心受压逐渐过渡到轴心受压，混凝土应变变化实现了连续过渡。区域③和区域④顶部混凝土边缘压应变保持不变，底部钢筋应变连续过渡。考虑二阶效应计算混凝土桥墩弹塑性承载力时，截面处于受压状态，不会出现轴心受拉或小偏心受拉，因此应变在区域②至区域⑤之间变化。

1.3 截面应力和内力计算

1）中性轴在截面内

对于区域②—区域④，矩形截面对称配筋受力构件见图2。

根据图2中应变的几何关系计算出截面的受压区高度x为

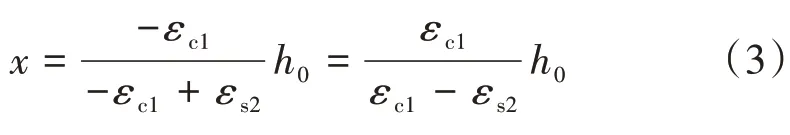
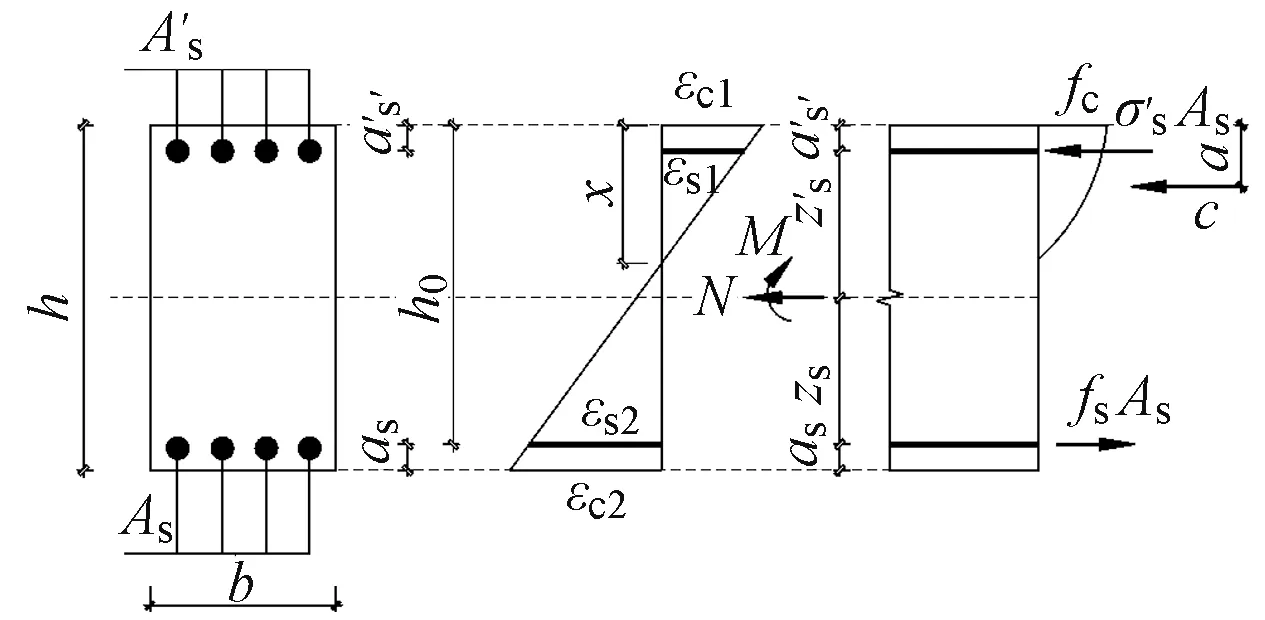
图2 矩形截面对称配筋受力构件

取x=kxh0，定义kx为受压区高度系数［10-11］，则

由平衡关系求得轴力N和弯矩M分别为

式中：σs和σ′s分别为钢筋的拉应力和压应力；αc为混凝土压应力不均匀系数［12］；zs和z′s分别为受拉钢筋合力力臂和受压钢筋合力力臂；a为混凝土受压区合力c作用点至截面受压区边缘的距离。

引入强度配筋率ωs=fyAs∕（fcbh），并对式（5）和式（6）进行量纲统一化处理［14］，得到无量纲轴力n和无量纲弯矩m为

αc的计算式为

定义ka为受压合力位置系数，则

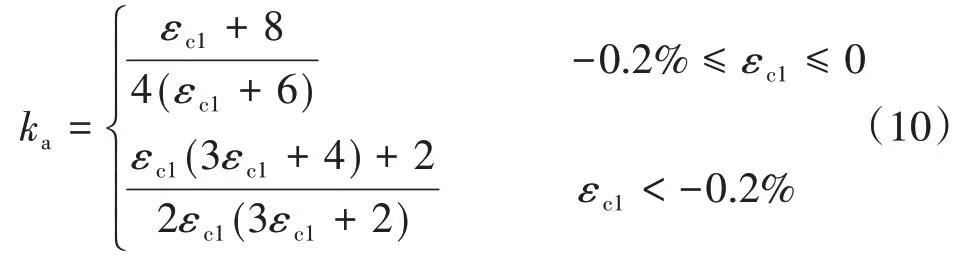
2）中和轴在截面下边缘外

对于区域⑤，矩形截面对称配筋小偏心受压构件见图3。

图3 矩形截面对称配筋小偏心受压构件

由平衡关系可得轴力和弯矩分别为

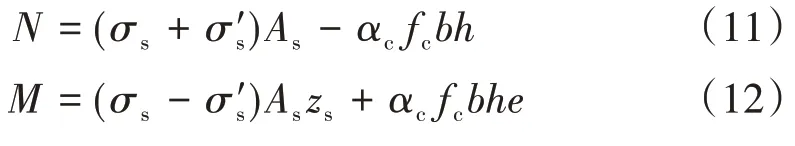
式中：e为偏心距。

对式（11）和式（12）进行量纲统一化处理，得到无量纲轴力和无量纲弯矩为

式中，e∕h为压力偏心率。

αc和e∕h的计算式分别为

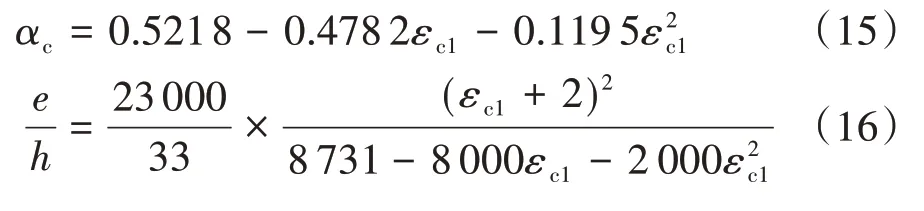
2 二阶效应mⅡ-n无量纲诺模图

计算钢筋混凝土桥墩正截面承载力时，若结构处于偏心受力状态，应考虑结构侧移和构件挠曲引起的附加内力［13］。因此，钢筋混凝土偏心受力构件内力设计时，参照规范第5.3.9 条引入偏心距增大系数η，以近似考虑二阶效应对截面内力增大的影响，即

式中：ea为附加偏心距；e0为初始偏心距；lc为构件的计算长度；ζ1为荷载偏心率对截面曲率的影响系数；ζ2构件长细比对截面曲率的影响系数。

将偏心距M∕N+ea用ηei代替，式（17）中附加偏心距ea取h∕30 与20 mm 两者的较大值。计算考虑二阶效应的混凝土桥墩弯矩MⅡ时，存在

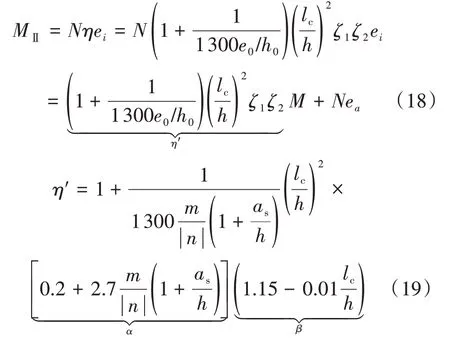
其中，α≤1.0，β≤1.0。

由式（18）可知，计算二阶弯矩MⅡ时可先不考虑附加偏心距的影响，只需在截面弯矩设计中叠加一项Nea即可。因此，只要给定墩柱构件lc∕h，就可以得到一组无量纲轴力n、无量纲二阶弯矩mⅡ与强度配筋率ωs之间的三维曲线，存在mⅡ=MⅡ∕η′。设墩柱采用HRB400 配筋，as∕h= 0.08，限于篇幅给出lc∕h= 14.4（即长细比λ=50）的mⅡ-n无量纲诺模图，见图4。

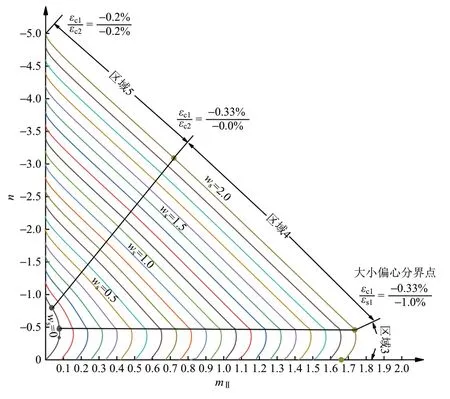
图4 考虑二阶效应矩形桥墩对称配筋诺模图

二阶效应mⅡ-n无量纲诺模图能够直接应用于工程设计，包括配筋设计和承载力复核，计算流程见图5。若弯矩承载力Mu大于荷载弯矩M，则截面强度满足要求，反之应调整配筋或增大截面。

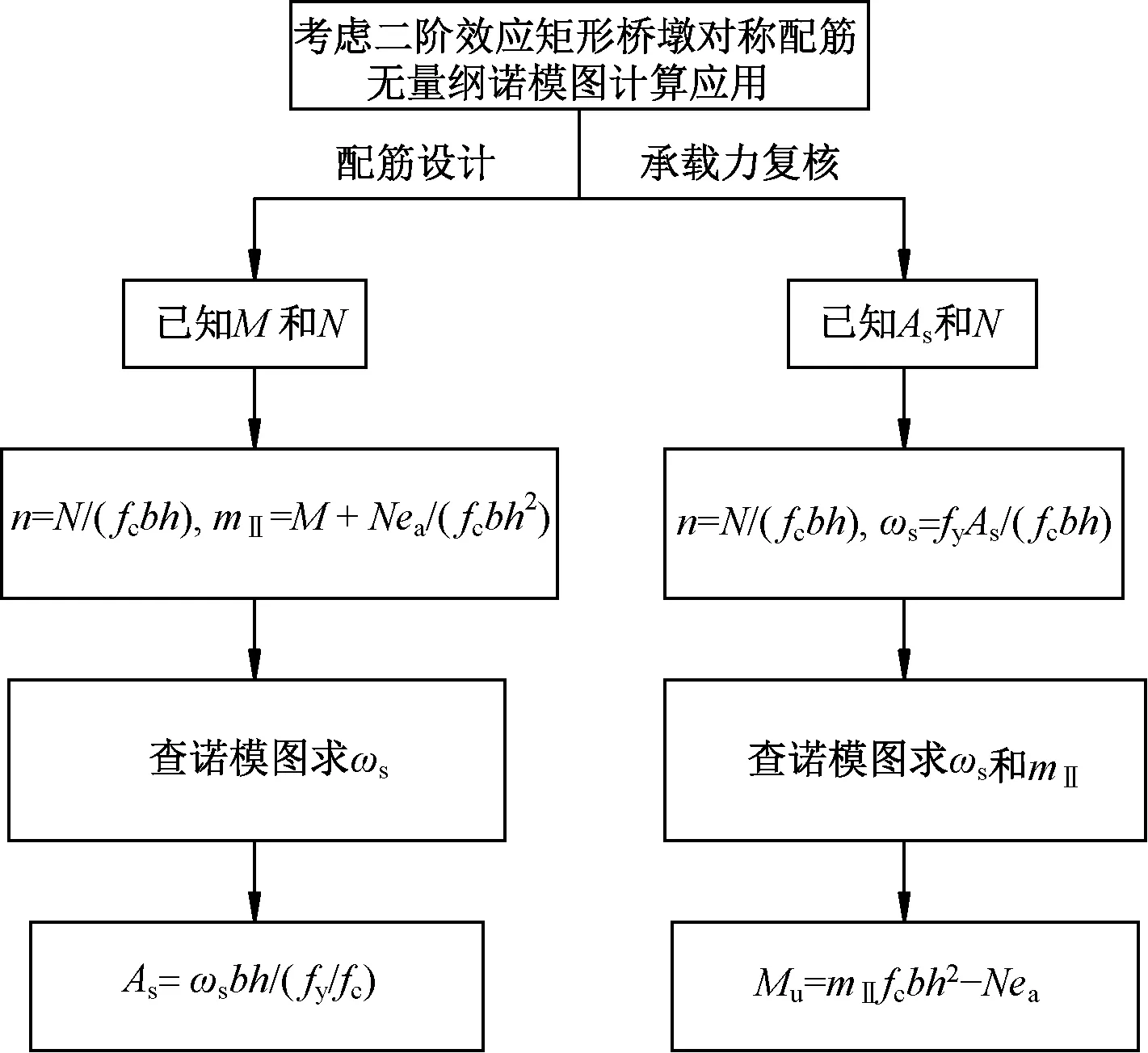
图5 设计计算流程

3 试验分析

为验证诺模图的正确性和可靠性，设计3 根钢筋混凝土试件进行了偏心受压试验，试件编号为A⁃1—A⁃3，初始偏心距分别为140，80，35 mm，截面尺寸（b×h）均为250 mm × 200 mm，纵筋均为6φ12，箍筋均为

S@75∕150。

为防止加载过程中试件端部混凝土局部承压破坏，在其上下端设置厚20 mm 的钢板。试件配筋与加载装置见图6。

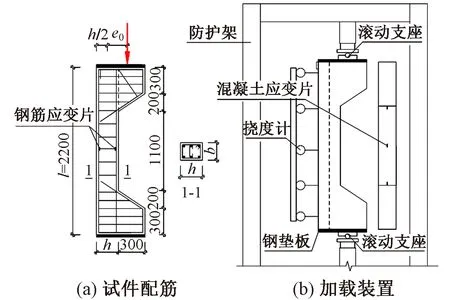
图6 试件配筋与加载装置（单位：mm）

3.1 试验现象

试验采用单调加载和等位移加载。A⁃1—A⁃2 试件均在受拉侧跨中先出现裂缝，随着施加荷载增大，裂缝宽度增大，数量增多，跨中挠度增大；荷载接近极限荷载时，受拉钢筋屈服，受压钢筋未屈服，混凝土被压碎，呈现大偏心受压构件的破坏特征。A⁃3 试件在跨中截面受拉边缘先出现细小裂缝，荷载接近极限荷载时受压边缘出现纵向裂缝，靠近加载侧受压钢筋屈服，远端钢筋未屈服，混凝土被压碎，呈现小偏心受压构件的破坏特征。A⁃1—A⁃2试件为大偏心受压破坏，A⁃3试件为小偏心受压破坏，见图7。

图7 试件破坏形式

在竖向加载过程中，钢筋混凝土构件均出现侧向挠曲。为了更好地了解考虑二阶效应的钢筋混凝土受压构件弹塑性承载力，根据各级加载值及对应跨中挠度绘制荷载和挠度的关系曲线，见图8。可知，随着偏心距的减小，试件逐渐从大偏心受压过渡到小偏心受压，破坏荷载逐渐提高。

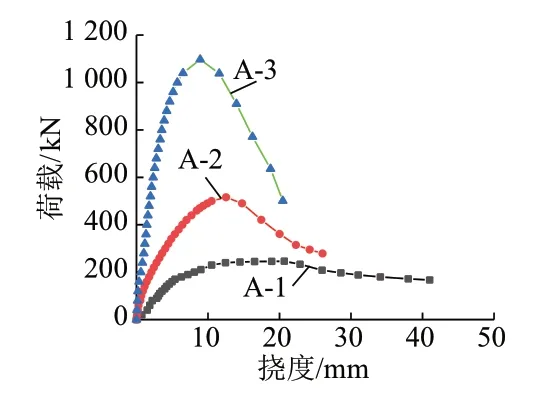
图8 荷载⁃挠度关系曲线

3.2 试验结果

根据图4 计算得到的极限承载力作为本文计算值，将3 个试件的极限承载力与本文计算值和规范计算值进行对比，见表2。可知，本文计算值与试验值吻合较好，相对误差的平均值为6.53%；规范计算值与试验值相对误差平均值为8.7%；与规范算法相比，本文算法精度稍有提高，能够很好地考虑二阶效应，钢筋混凝土矩形截面承载力计算结果准确可靠。

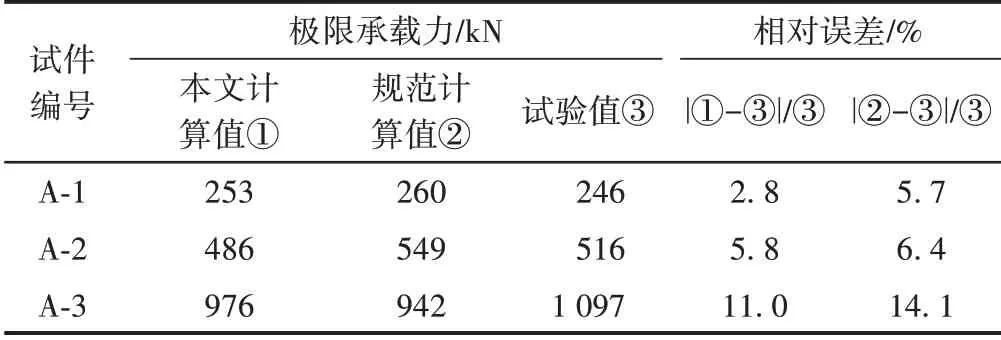
表2 构件截面承载力对比分析结果

4 应用算例

4.1 配筋设计

偏心受压矩形截面柱墩b×h=300×500 mm，as=a′s=40 mm，墩柱计算高度为7 750 mm，混凝土强度等级为C30，fc=14.3 MPa，钢筋为HRB400，fy=360 MPa。作用荷载组合：①M= 600 kN·m、N= -800 kN；②M=102.4 kN·m、N= -800 kN。考虑二阶效应，采用本文方法对两种荷载组合下的构件进行配筋计算，参考图5计算流程，得到构件相关参数见表3。

4.2 承载力复核

矩形截面混凝土柱墩b×h= 300 × 500 mm，as=a′s=40 mm，墩柱计算高度为8 650 mm，混凝土强度等级为C30，采用HRB400钢筋对称配筋，As=A′s=2 945 mm2，轴力设计值N=-1 280 kN，弯矩设计值M=300 kN·m，采用本文方法验算截面抗弯强度是否满足要求。具体步骤为：

1）求解名义轴力n和强度配筋率ωs。n=N∕（fcbh）=-0.597，ωs=fyAs∕（fcbh）=0.494。

2）根据as∕h= 0.08，lc∕h= 8 650∕500 = 17.3，查图4得mⅡ=0.42。

3）确定截面抗弯承载力。附加偏心距ea取20 mm，则Mu=MⅡ-Nea=mⅡfcbh2-Nea= 450.5 - 25.6 =424.9 kN·m ＞300 kN·m。该柱墩正截面抗弯强度满足要求。

通过以上算例可以看出：考虑二阶效应时，采用本文方法对钢筋混凝土矩形截面桥墩进行配筋计算，无需判别是大偏心受压还是小偏心受压，不用求解大量二阶效应参数；承载力复核时，无需进行复杂的试算，能够快速方便地计算二阶效应弯矩。