基于顶底板刚度差异的混凝土箱梁收缩效应试验研究
2021-03-14李珍周勇军赵煜卫愿康赵洋
李珍 周勇军,2 赵煜,2 卫愿康 赵洋
1.长安大学公路学院,西安 710064;2.长安大学公路大型结构安全教育部工程研究中心,西安 710064;3.河南省交通规划设计研究院股份有限公司,郑州 450052
随着使用年限的增加,预应力混凝土箱梁出现了不同程度的下挠和开裂现象,不仅影响了行车的舒适性,而且降低了结构的耐久性,对桥梁结构的安全运营造成了威胁,后期的维修加固难度风险极大[1]。关于预应力混凝土箱梁桥的下挠和开裂病害,国内外专家认为主要有三方面原因:收缩徐变效应、钢筋应力松弛、计算方法的差异。其中,收缩徐变的不确定性是导致预应力混凝土箱梁桥长期挠度变形不能准确预测的主要原因[2]。
关于混凝土箱梁桥非均匀收缩效应,国内外学者做了很多研究。文献[3-8]利用有限元软件考虑混凝土箱梁不同部位的收缩差异,研究非均匀收缩对混凝土箱梁桥长期下挠的影响,发现考虑非均匀收缩计算的跨中挠度比不考虑时大,计算模型较好地模拟了实际箱梁桥收缩特性。文献[9]进行了工字型构件的非均匀试验,并基于湿度场理论考虑箱梁桥的非均匀收缩效应,发现箱梁截面非均匀收缩会产生挠曲变形。而文献[10-11]的研究结果却表明混凝土箱梁桥各部位收缩差异对主梁下挠带来的影响较小。由此可见,对非均匀收缩引起的混凝土箱梁桥长期挠曲变形问题还没有统一的结论,并且缺乏箱梁收缩试验验证。
本文通过不同顶底板刚度下的混凝土箱梁收缩效应试验,基于湿度场理论,采用有限元软件对节段箱梁收缩效应进行模拟,研究构件的收缩曲率变化规律并与试验结果对比分析,研究成果可为混凝土箱梁桥长期挠曲变形提供参考。
1 试验概况
1.1 试验构件的设计与制作
试验只考虑顶底板刚度(厚度)差异对箱梁收缩效应的影响。对于实际工程中的大跨度混凝土箱梁,一般顶板厚度为250 mm 左右,底板厚度为200~1 000 mm,顶底板厚度比在1∶1~1∶4。因此,本文选择顶底板厚度比为1∶1、1∶2、1∶3的三组节段箱梁构件进行试验,顶底板刚度比分别为1∶0.6、1∶4.8、1∶16.2,试验组编号分别为BS⁃60、BS⁃120、BS⁃180,每组三个构件,见图1。三组构件顶板、腹板尺寸厚度均为60 mm,底板厚度分别为60、120、180 mm。节段箱梁构件均竖直放置,自重作用引起试验构件的徐变变形很小,可忽略不计。
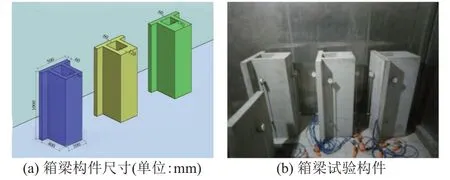
图1 试验构件
1.2 混凝土材料及配合比设计
混凝土设计强度等级为C50,配合比见表1。混凝土节段箱梁浇筑成型后,设置环境实验室内为标准养护条件[(温度为(20 ± 2)℃、相对湿度为95%以上],养护3 d 后,安装并调试测试装置,将环境条件设置为测试条件[温度为(20±2)℃、相对湿度为(60±5)%]开始进行收缩测试,此后控制测试环境为恒温恒湿。

表1 混凝土配合比
1.3 试验测试
测试箱梁各部分的应变,并实时监测温度、湿度。混凝土内部采用内部预埋振弦式应变计和外部大标距引伸计(千分表)进行应变测量。测点布置见图2。

图2 箱梁测点布置
2 试验结果与分析
混凝土箱梁顶底板的收缩应变取3个内部预埋振弦式应变计测得的平均值。左右腹板收缩应变取相应板件中部的1 个内部预埋振弦式应变计测试值,同时用外部的引伸计对内部振弦式传感器读数进行校准。试验结果取一组3个构件的算术平均数作为该混凝土在各龄期时的收缩应变。由于混凝土构件、振弦式应变计钢弦和大标距引伸计的线膨胀系数不同,在试验过程中,若环境温度前后两次存在差值,两者产生的热胀冷缩变形会有所差异。因此,在实际测量值中包含了由于温度变化造成的应变差,须对其进行温度修正。节段箱梁构件共监测了90 d。
2.1 箱梁构件收缩试验结果
箱梁构件实测收缩应变发展曲线见图3。可知:①BS⁃60 组箱梁各部位收缩规律基本一致,各龄期收缩应变差较小,表明顶底板在收缩历程中近似呈均匀收缩;箱梁各部位前期收缩发展速度快,后期收缩速度减缓,最终趋于平稳状态。②BS⁃120 组箱梁顶板和底板收缩规律存在差异,顶板在各龄期的收缩应变均比底板大,顶底板呈非均匀收缩。在收缩发展前期,顶底板的收缩应变差随着龄期增大而增大,在龄期达到30 d 左右时收缩应变差达到极值,后期收缩应变差减小,这表明顶板早期收缩发展迅速而后期减缓,底板则因厚度大,前期收缩发展缓慢,后期仍有发展趋势。③BS⁃180 组箱梁顶板与底板的收缩应变差比BS⁃120 组更大,箱梁顶底板的非均匀收缩更加明显。与BS⁃120组不同的是,箱梁顶底板收缩应变差达到极值的龄期不同,因为BS⁃180 组底板更厚,底板收缩发展相对缓慢,所以达到收缩应变差极值的时间有所推迟,龄期50 d左右时到达最大。

图3 箱梁构件实测收缩应变发展曲线
2.2 箱梁构件收缩曲率
不同顶底板刚度比对节段箱梁曲率的影响不同,节段箱梁的顶底板收缩应变差表明了箱梁构件在试验期间不仅发生轴向缩短,还发生了弯曲变形,这种弯曲变形的程度可用曲率表示。在平截面假定的情况下,曲率κ只和顶底板的应变差有关,其计算式为

式中:εt、εb分别为顶板、底板的收缩应变;H为箱梁截面高度。
箱梁构件收缩曲率曲线见图4。可知:①顶底板刚度比对节段箱梁收缩产生的曲率有较大影响。当顶底板刚度差异不大时,箱梁收缩基本上不产生额外的曲率;当顶底板刚度差异较大时,收缩差异会导致曲率变化较大。箱梁收缩前期曲率增长较快,随着龄期的发展,增长速率减缓,达到曲率峰值点后开始减小,但是减小速率较慢。②箱梁曲率达到峰值点的时刻与顶底板刚度相关,顶底板刚度差异越大,越晚达到峰值点,BS⁃120 组箱梁构件在30 d 龄期达到峰值,BS⁃180 组则在53 d 到达峰值。③曲率峰值随顶底板刚度差异的增大而增大,BS⁃180 组的曲率峰值是BS⁃120组的2倍以上。

图4 箱梁构件收缩曲率曲线
2.3 典型收缩预测模型计算值与实测值对比分析
计算箱梁收缩通用的理论方法是将箱梁全截面的理论厚度作为计算基础。该理论模型采用JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》[12]中的模型。
为了验证箱梁各部位收缩的差异性,将顶底板实测应变和全截面理论应变进行对比,见图5。可知,按照规范全截面理论计算的顶底板收缩值与实测值差距较大,说明与实际情况不相符,且顶板理论计算值与实测值的相对误差普遍比底板大,最高可达50%以上。

图5 各组箱梁收缩实测值与模型理论计算值对比
3 节段箱梁在湿度场下的收缩效应分析
混凝土在干燥、硬化过程中,结构内部和外界环境在湿度梯度下不断地发生水分转移,直到内外湿度达到平衡。混凝土内部湿度变化引起了体积变化,导致结构产生非均匀收缩变形。这一过程中内部水分扩散服从Fick定律[13-15],因此,可通过湿度场理论对混凝土构件的收缩过程进行计算分析,研究混凝土内部湿度扩散过程和混凝土箱梁结构的非均匀收缩规律。
3.1 混凝土湿度场模拟
混凝土的湿度场可以用温度场替代求解,但前提是把两个场的各物理量对应起来。通过对比发现,相对湿度对应于温度,湿度扩散系数可用导温系数替代,表面因子可用热交换系数替代,收缩系数可用热膨胀系数替代[16]。本文通过ABAQUS 有限元软件进行混凝土湿度场下收缩效应的求解与分析。
3.2 计算参数的选择及基本假定
混凝土湿度场的主要计算参数如湿度扩散系数、表面因子和收缩系数,与试验材料和环境因素有关,很难确定其精确数值。因此,如要对混凝土湿度场下的收缩效应进行精确模拟,必须选择合适的计算参数,因此作如下假定与参数取值说明:
1)试验采用的材料是水胶比较大的普通混凝土,因此只考虑由于水分散发引起的干燥收缩,不考虑其他类型的收缩;试验的环境温度为标准试验温度,且试件较小、水化热少,忽略温度对湿度场的影响。
2)湿度扩散系数D(H)取常数,收缩应变与湿度之间的关系采用线性模型。
3)表面因子f和收缩系数ksh根据试验结果进行反演分析获得。
4)收缩应变主要由湿度变化和收缩系数确定,与弹性模量相关性不强,所以假定混凝土收缩过程中弹性模量为定值。
国内外有关研究表明,湿度扩散系数D(H)、表面因子f和收缩系数ksh在试验条件下无法确定时,其数值 参 考 范 围[16]为:12 ≤D(H)≤360,0.05 ≤f≤80,0.5× 10-3≤ksh≤3× 10-3。
在给定参数范围内根据试验数据进行湿度场的计算参数反演,得到能准确模拟试验过程的计算参数,其中湿度扩散系数因缺乏试验数据,可取中位数。参数试算流程见图6。

图6 参数试算流程
具体步骤为:将混凝土材料属性中的密度和比热容都设为1,将湿度场和温度场对应起来,假定f、ksh参数值进行湿度场的求解。利用热-位移耦合关系计算收缩效应,将有限元计算值与实测值进行对比,使两者接近。建立两个分析步模拟试验过程的环境情况,分别为构件养护阶段和测试阶段。经计算分析选取后,节段箱梁湿度场的计算参数见表2。

表2 混凝土湿度场计算参数
将箱梁顶底板实测收缩应变曲线与有限元计算收缩应变曲线进行对比,见图7。可知,在有限元计算结果中,BS⁃60 组箱梁顶底板收缩发展趋势基本一致,BS⁃120组箱梁、BS⁃180组箱梁的顶板和底板收缩规律不同,顶板的收缩应变比底板大,顶板的收缩速率逐渐减小,而底板基本上成线性发展,这与实测值基本一致。误差在13%~30%。

图7 箱梁顶底板收缩应变有限元计算值和实测值对比
3.3 湿度场模拟结果
三组箱梁在第90 天的湿度分布云图见图8。可知:混凝土的湿度扩散速度随深度的增加而减小,由于表面直接与空气接触,所以湿度散失较快,内部湿度到达表面的路径较长,因此湿度变化较缓慢;随着顶底板刚度差异的增大,箱梁截面的湿度梯度增大。

图8 箱梁构件90 d湿度分布云图
箱梁曲率有限元计算值与实测值对比见图9。可知,二者变化规律基本一致,且误差在一定范围之内,表明采用湿度场模拟节段箱梁的收缩曲率具有可行性;箱梁曲率有限元计算值与实测值的差异主要体现在峰值曲率以及峰值出现时间。对于数值上的差异,主要是由于各组箱梁之间材料的不均匀、试验过程中周围环境的变化导致的。对于峰值出现时间,这是由于试验过程中打开了循环风机,风速加速了箱梁的收缩。

图9 箱梁曲率有限元计算值与实测值对比
4 结论
1)节段箱梁的顶底板刚度不同时,其产生的收缩规律不同。当顶板和底板的刚度差异较小时,箱梁的各部位收缩基本同步发展,只产生轴向变形,不产生额外的曲率。
2)当顶板和底板的刚度差异较大时,各部位产生收缩应变差,从而导致节段箱梁产生收缩曲率。曲率呈先增大后减小的变化趋势,收缩曲率达到峰值的时间不一致,顶底板刚度差异越大,其达到峰值的时间越晚,但其相应的曲率极值越大。
3)按照全截面计算箱梁收缩值与顶底板的实际收缩值差距较大。
4)湿度梯度是箱梁截面产生收缩差异的直接原因。采用湿度场模拟所得箱梁收缩曲率与实测值基本一致,且误差在一定范围之内,该方法具有可行性。
