基于LPN困难问题的后量子安全公钥加密
2021-03-14徐胜峰李祥学
徐胜峰,李祥学,2
(1.华东师范大学 计算机科学与技术学院,上海 200062; 2.华东师范大学 软件工程学院,上海 200062)
LPN(Learning Parity with Noise)问题在后量子密码领域是一个常用的假设[1],主要用来构造一些加密算法和协议,如公钥加密算法和传输协议等。这些基于LPN构造出来的加密算法和协议性能高并能抵抗量子算法的攻击。


Alekhnovich[19]最早构造出基于低噪LPN的选择明文攻击下的不可区分(Indistinguishability against Chosen Plaintext Attack,IND-CPA)安全的公钥加密方案。随后,Döttling等人[11]利用相关认证技术[20]首次构造出基于低噪LPN的选择密文攻击下的不可区分(Indistinguishability against Chosen Ciphertext Attack,IND-CCA)安全的公钥加密方案,但是方案的公钥、私钥和密文长度过大,效率有待提高。Kiltz等人[21]利用双陷门技术构造出IND-sTag-CCA安全的带标签公钥加密方案,并将该方案通过常见的技术手段转变成IND-CCA安全的公钥加密方案。双陷门技术在方案的安全性证明中用来回答敌手的解密询问。这两个IND-CCA安全的公钥加密方案的解码错误率(Decoding Failure Rate,DFR)均是2-Θ(k),k为安全参数。Yu等人[14]构造出基于常噪LPN问题的CCA安全公钥加密方案的解码错误率为2-Θ(k2)。
到目前为止,并没有基于变体xLPN(Variant of the Exact LPN,VxLPN)的CPA/CCA安全的公钥加密方案。因此,该研究拟证明VxLPN问题和标准LPN问题一样困难,并通过双陷门技术,构造基于VxLPN的IND-CPA/CCA安全的公钥加密方案,以期降低解码错误率,提高效率。
1 预备知识
1.1 符号描述
为了表述方便,对文中符号进行描述。黑体小写字母表示列向量,如s,黑体小写字母的转置表示行向量,如sT。列向量s的汉明重量表示为|s|。黑体的大写字母表示矩阵,如A,黑体大写字母的转置表示矩阵的转置,如AT。μ表示噪声率为μ的伯努利分布,也就是Pr[μ=1]=μ,Pr[μ=0]=1-μ,表示q个独立的副本,也就是μ并列起来。表示列向量从分布{z∈{0,1}q∶|z|=qμ}上均匀地选取出,其中,qμ表示向量汉明重量为qμ。表示矩阵中的每一列都是从分中均匀选取的,x表示x中均匀随机选取。Uq(Uq×q)表示在{0,1}q({0,1}q×q)上的均匀分布。negl(·)为其输入的可忽略函数。
1.2 LPN及相关变体的定义
该部分主要介绍LPN问题、变体LPN问题(Variant of the LPN,VLPN)、紧凑LPN问题(Exact LPN,xLPN)以及背包LPN问题(Knapsack LPN,KLPN)相关定义。


(1)


(2)

困难性令T:=T(n),如果运行时间限制为T,对于任意攻击者的优势在式(1)和式(2)中的上界为1/T,判定性/计算性(n,μ,q)-LPN问题是T-困难的。对于(n,μ)-LPN问题,内在的限制就是q≤T。
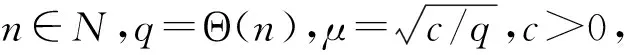



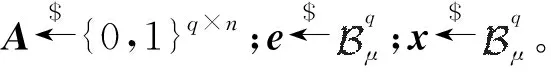
判定性(n,μ)-VLPN问题可以规约到判定性(n,μ)-LPN问题上,详细证明过程参考文献[11]。



判定性(n,μ)-KLPN问题可以规约到判定性(n,μ)-LPN问题,详细证明过程参考文献[22]。


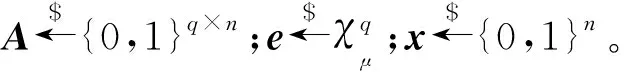

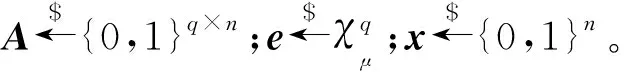
判定性(n,μ)-xLPN问题可以规约到判定性(n,μ)-LPN问题,详细证明过程参考文献[8]。
类似于定义1与定义2的关系,可以给出VxLPN问题的定义。
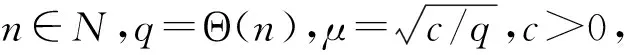




Abhishek等人[23]证明出判定性(n,μ)-xLPN问题和计算性(n,μ)-LPN问题是多项式等价的。证明VxLPN问题的困难性的具体规约过程如下。

下面将在引理A中证明判定性(n,μ)-VxLPN问题和计算性(n,μ)-VxLPN问题一样困难。在引理B中证明计算性VxLPN和计算性VLPN一样困难。


要证明判定性(n,μ)-VxLPN问题和计算性(n,μ)-VxLPN问题是等价的,常用的关于判定性(n,μ)-LPN问题的规约方法[2]不适用于判定性(n,μ)-VxLPN问题,因此,利用Goldreich-Levin理论[24]完成规约证明。
引理B 判定性(n,μ)-VxLPN问题和计算性(n,μ)-VxLPN问题是多项式等价的。
证明根据样例保存规约证明该引理。利用标准的技术[4],证明判定性矩阵版本(n,μ)-VxLPN问题也是困难的。证明方案的安全性就是利用判定性(n,μ)-VxLPN问题和判定性矩阵版本(n,μ)-VxLPN问题。下面,将具体证明该引理。


情况1矩阵A′是一个q×n随机矩阵。
情况2y=Ax+e=A′x+srTx+e=A′x+s〈r,x〉+e。

这样能得到一个关于Goldreich-Levin理论的矛盾,假设是不存在的。综上所述,完成了该引理的证明。
1.3 哈希函数和随机预言机模型





1.4 公钥加密方案
公钥加密[25-27](Public Key Encryption,PKE)方案是一个概率多项式时间算法元组(Gen,Enc,Dec),其定义如下。
1)密钥生成算法Gen是一个概率算法,该算法需要输入安全参数1k,输出公钥kp和私钥ks。
2)加密算法Enc是一个概率算法,该算法需要输入公钥kp和明文p,输出密文C,记为C←Enc(kp,p)。
3)解密算法Dec是一个确定的算法,该算法需要输入私钥ks和密文C,输出明文p或者失败符号⊥,记作p←Dec(ks,C),并满足
Pr[Dec(ks,(Enc(kp,p)))≠p∶(kp,ks)←Gen(1k)]=
negl(k)
等式不成立的概率是可忽略的,这是由(kp,ks)和加密算法使用的任何随机数所决定。
带标签的公钥加密[28-30](Tag Based public key Encryption,TBE)方案是一个概率多项式时间算法元组(KeyGen,Enc,Dec),其定义如下。
1)密钥生成算法KeyGen是一个概率算法,该算法需要输入安全参数1k,输出公钥kp和私钥ks。

3)解密算法Dec是一个确定的算法,该算法需要将私钥ks和密文C作为输入,输出明文p或者失败符号⊥,记作p←Dec(ks,t,C),并满足
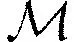
等式不等的概率是可忽略的,这是由(kp,ks)和加密算法使用的任何随机数所决定的。
1.5 公钥加密方案安全性定义

初始化挑战者输入安全参数1k,并生成挑战密钥对(kp,ks)←Gen(1k),攻击者从挑战者手中得到公钥kp,挑战者随机选择b∈{0,1}。
挑战挑战者收到了攻击者发送过来的等长消息对(p0,p1),生成挑战密文C*←Enc(kp,pb),并将生成的挑战密文发送给攻击者。


初始化挑战者输入安全参数1k,并生成挑战密钥对(kp,ks)←Gen(1k),攻击者从挑战者手中得到公钥kp,挑战者随机选择b∈{0,1}。



1.6 带标签的公钥加密方案安全性定义

初始化挑战者输入安全参数k,并从攻击者手中获得一个标签t*。
密钥生成挑战者计算出密钥(kp,ks)←Gen(1k),将密钥ks单独保留,并将公钥kp发送给攻击者,随机选取




初始化挑战者输入安全参数k,并从攻击者手中获得一个标签t*。
密钥生成挑战者计算出密钥(kp,ks)←KeyGen(1k),将密钥ks私自保留,并将公钥kp发送给攻击者,随机选取挑战比特





那么TBE方案是IND-sTag-CCA2安全的。
1.7 主要引理

引理2(布尔不等式)[33-35]对于事件A1,A2,…,Aq,有

证明假设e的汉明重量不超过2 μm,分析sTe结果的情况。sTe=1必要条件是至少存在一个i且当s[i]=1时,e[i]=1。将该必要条件应用在下面证明第二步中,布尔不等式[33-36]应用在第四步中,最终得到

令δ:=α/(4μ′)-1,注意到μ′≤c<α/4,(1+δ)μ′=α/4,使用切诺夫不等式可以得到
不难发现δ=α/(4μ′)-1≥α/(4c)-1>0和δμ′=α/4-μ′>c-μ′≥0均为大于零的常量,可以得到
将矩阵E表示为(e1,e2,…,em),则ETs=[sT(e1,e2,…,em)]T。用类似的方法证明
其中,|ETs|=|(sTe1,sTe2,…,sTem)T|,具体证明细节省略。

根据判定性(n,μ)-LPN假设,(A,yTA)和(A,r)是计算不可区分的,证明过程参考文献[37]。
2 基于LPN的CPA安全的公钥加密
下面介绍3个常见的基于LPN的CPA安全的公钥加密方案,包括Alekhnovich的方案[19](简称AM方案)、Döttling等人[11]的方案(简称DMN方案)和Yu等人的方案[14](简称YZ方案),以及该研究构造的基于VxLPN的IND-CPA安全的公钥加密方案。
2.1 AM方案
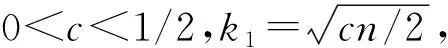


C=Ty+e
其中,C∈{0,1}m。
3)Dec(ks,C):解密算法。输入私钥ks=(S,E)和密文C,并通过解码算法从密文C中恢复出v。利用求解线性系统v=MTTy计算出y。如果|e|满足|e|≤αm,那么解密算法输出p,否则,解密算法输出⊥。
AM方案是首个基于LPN的CPA安全公钥加密方案,其正确性和安全性证明参考文献[19]。
2.2 DMN方案



3)Dec(ks,C):解密算法。输入私钥ks=T和密文C=(c1,c2,c3),计算c0:=c2-Tc1。
解密算法利用生成矩阵G的纠错性质恢复出s。如果解码失败,输出⊥,否则解密算法利用生成矩阵G1的纠错性质恢复出p。如果两次解码都正确,则输出p,否则输出⊥。
DMN方案的正确性和安全性证明参考文献[11]。
2.3 YZ方案
Yu等人[14]首次构造出基于常噪LPN的CPA安全的公钥加密方案,在此基础上利用相关技术又构造出基于常噪LPN的CCA安全带标签的公钥加密方案。令k是方案的安全参数,选取正整数m和n分别满足n=Θ(k2)和m=Θ(k2),噪声率0<μ<1/2,生成矩阵G∈{0,1}m×n能够纠αm个错误。YZ方案的具体算法如下。


3)Dec(ks,C):解密算法。输入私钥ks=s和密文C=(C1,c2),并计算
解密算法利用生成矩阵G的纠错性质恢复出明文p。如果有|STe-ETs|≤αm,则输出p,否则输出⊥。
YZ方案的正确性和安全性证明参考文献[14]。
2.4 基于VxLPN的IND-CPA安全公钥加密方案



3)Dec(ks,C): 解密算法。输入私钥ks=s和密文C=(C1,c2),并计算

定理1只要方案选择适当的参数,PKE方案就能够满足正确性。

下面将分析密文C。由引理3可以得到概率为1-2-Θ(m)的等式

定理2如果判定性(n,μ)-VxLPN假设是困难的,那么PKE方案是IND-CPA 安全的。

游戏0该游戏是关于PKE方案的IND-CPA安全实验。挑战者模拟IND-CPA安全游戏如下。

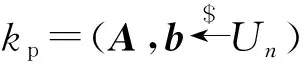

和游戏2中的
在计算上是不可区分的。因此,可以得到|Pr[R2]-Pr[R1]|≤negl(n)。
因此,PKE方案满足IND-CPA安全。
3 基于LPN的CCA安全的公钥加密
下面介绍4个常见的基于LPN的CCA安全的公钥加密方案,包括DMN方案[11]、Kiltz等人[21]的方案(简称KMP方案)、YZ方案[14]和Cheng等人[12]的方案(简称CLQY方案),以及该研究构造的基于VxLPN的IND-CCA安全的公钥加密方案。
3.1 DMN方案




解密算法利用生成矩阵G的纠错性质恢复出s。如果解码失败,输出⊥,否则计算e1=c1-As、e2=c2-Bτ′s和e3=c3-Ds-G1p。解密算法利用生成矩阵G1的纠错性质恢复出p,如果两次解码都正确,则输出p,否则输出⊥。
在128比特安全下,DMN方案的公钥和私钥长度往往会比其他基于LPN的 CCA安全的公钥加密方案的公钥和私钥长度大得多。该方案的正确性和安全性证明参考文献[11]。
3.2 KMP方案



3)Dec(ks,C,t):解密算法。输入私钥ks=(0,T0)、标签t和密文C=(c,c0,c1,c2),解密算法计算

则使用生成矩阵G1的纠错性质恢复出明文p(从c2-Ds=G1p+e1中恢复),否则令p=⊥。最后,输出明文p。
KMP方案的正确性和安全性证明参考文献[21]。
3.3 YZ方案
Yu等人[14]构造出首个基于常噪LPN的CCA安全带标签的公钥加密方案,使用双陷门技术又成功构造出CCA安全的加密方案,并利用相关技术将该CCA安全的带标签的公钥加密方案转换成CCA安全的公钥加密方案。令k为方案的安全参数,选取一些常数n=Θ(k2),m≥2n,l≥m,q=Θ(n),除此之外,令α为常数且满足α>0,噪声率0<μ≤0.1,μ1=Θ(logn/n),λ=Θ(log2n),2λ≤H∞(生成矩阵G∈{0,1}m×n和G1∈{0,1}l×n分别能纠正βm和2μl个比特错误[14]。定义标签空间=F2n,Ht∈{0,1}n×n,t,t1,t2∈F2n,满足H0=0,Ht1+Ht2=Ht1+t2,给定任何t≠0可计算出Ht。YZ方案的具体算法如下。


c:=As+e
c0:=(GHt+B0)s+(S′0)Te-(E′0)Ts
c1:=(GHt+B1)s+(S′1)Te-(E′1)Ts
c2:=Ds+e1+G1p
其中,c∈{0,1}n,c0∈{0,1}m,c1∈{0,1}m,c2∈{0,1}t。


则使用生成矩阵G1的纠错性质恢复出明文p(从c2-Ds=G1p+e1中恢复),否则令p=⊥。最后,输出p。
YZ方案的正确性和安全性证明参考文献[14]。
3.4 CLQY方案




c0-Tc=GHts+(T′-T)e
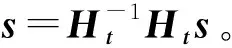
CLQY方案的正确性和安全性证明参考文献[12]。
3.5 基于VxLPN的IND-CCA安全公钥加密方案
该研究将构造基于VxLPN的IND-CCA安全的公钥加密方案,为此首先构造基于VxLPN的IND-sTag-CCA2安全的公钥加密方案,在此基础上再利用标准的变换[14,21,40]将带标签的公钥加密方案转变成标准的公钥加密方案。


(kp,ks) =[(A,B0,B1,D),(S0,S1)]

c:=As+e
c0:=(GHt+B0)s+(S′0)Te-(E′0)Ts
c1:=(GHt+B1)s+(S′1)Te-(E′1)Ts
c2:=Ds+e1+G1p
其中,c∈{0,1}n,c0∈{0,1}m,c1∈{0,1}m,c2∈{0,1}l。


(3)
则使用生成矩阵G1的纠错性质恢复出明文p(从c2-Ds=G1p+e1中恢复),否则令p=⊥。最后,输出p。

定理3只要方案选择适当的参数,TBE方案是正确的。
证明要想得到正确的TBE方案,需要满足以下条件

|(S′0-S0)Te+(E0-E′0)Ts|≤αm
|e1|=μl

Pr[|e|=μn]=1
Pr[|e1|=μl]=1
则C是正确生成的密文。由引理3以压倒性的概率得到

中解码出正确的Hts,且错误项满足
|(S′i-Si)Te+(Ei-E′i)Ts|≤αm,

定理4如果判定性(n,μ)-VxLPN假设是困难的,那么TBE方案是IND-sTag-CCA2安全的。



使用生成矩阵G的纠错性质恢复出Hts。如果有




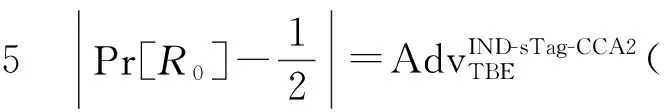

游戏1该游戏和游戏0基本一致,除了挑战者改变密钥生成阶段。
引理6|Pr[R1]-Pr[R0]|≤negl(n)
证明游戏1和游戏0唯一的不同就是挑战者用游戏1公钥中代替游戏0公钥中根据矩阵版本判定性(n,μ)-VxLPN假设,游戏1中和游戏0中kp=(A,B0,B1,D)是计算不可区分的。因此,|Pr[R1]-Pr[R0]|≤negl(n)。
游戏2该游戏和游戏1基本一致,除了挑战者改变密钥生成阶段和挑战阶段。


引理7Pr[R2]=Pr[R1]
证明游戏2和游戏1不同的是,挑战者在游戏2公钥中用代替了游戏1公钥中此外,S1和E1在密钥生成阶段中与S′1和E′1在挑战阶段具有相同的分布。不难发现,并不包含在公钥中,所以攻击者不能得到任何关于S1和E1有用的信息。游戏2中的挑战密文和游戏1中的挑战密文具有相同的分布。综上所述,在攻击者看来,游戏2和游戏1相同,所以有Pr[R2]=Pr[R1]。
游戏3该游戏和游戏2基本一致,除了挑战者改变密钥生成阶段。
引理8|Pr[R3]-Pr[R2]|≤negl(n)
证明游戏3和游戏2唯一的区别就是挑战者在游戏3公钥中用代替游戏2公钥中其中根据矩阵版本判定性(n,μ)-VxLPN假设,在攻击者看来,游戏2中公钥和游戏3中公钥是计算不可区分的。因此,不难得到|Pr[R3]-Pr[R2]|≤negl(n)。值得注意的是,挑战密文中
游戏4该游戏和游戏3基本一致,除了挑战者利用S1代替S0来响应所有的解密查询。
引理9|Pr[R4]-Pr[R3]|≤negl(n)
证明不难知道,S1和S0有等价的解密能力且恢复出相同明文的概率差不超过关于n的可忽略函数。
游戏5该游戏和游戏4基本一致,除了挑战者改变密钥生成阶段和挑战阶段。


引理10|Pr[R5]-Pr[R4]|≤negl(n)
证明由引理6-9相似的方法可证明该引理。
游戏6该游戏和游戏5基本一致,除了挑战者改变挑战阶段。

引理11|Pr[R6]-Pr[R5]|≤negl(n)
证明游戏6和游戏5唯一的区别就是挑战者在游戏6中用c*:=v和代替游戏5中的c*:=As+e和其中:根据判定性(n,μ)-VxLPN假设是困难的,游戏6挑战密文与游戏5中挑战密文是计算不可区分的。因此,可得到|Pr[R6]-Pr[R5]|≤negl(n)。

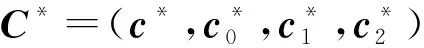
3.6 IND-CCA安全的公钥加密方案的性能分析
由于IND-CPA安全的公钥加密方案构造相对比较简单,因此主要分析IND-CCA安全的加密方案的性能。DMN方案[11]、KMP方案[21]、YZ方案[14]、CLQY方案[12]和构造方案的困难问题假设如表1所示。DMN方案[11]、KMP方案[21]和构造方案的解密错误率如表2所示。在DMN方案[11]、KMP方案[21]和构造方案中,令n=k2,m=2n,在DMN方案[11]中,令l1=l2=l3=n。

表1 不同方案的困难问题假设

表2 不同方案的解码错误率



表3 不同方案的参数对比
4 结语
研究了基于变体xLPN的CPA/CCA安全的加密方案。在几个比较常见的基于LPN问题的CPA/CCA安全的公钥加密方案的基础上,利用双陷门技术构造出了基于VxLPN问题的CPA/CCA安全的加密方案。利于一次签名可以直接构造出CCA安全的公钥加密方案,而双陷门技术可以构造出CCA安全带标签的公钥加密方案,通过转换可以得到CCA安全的公钥加密方案。性能分析表明,在128比特安全水平下,Döttling等人[11]和Kiltz等人[21]方案的公钥长度、私钥长度、密文长度分别为(14.53 GB、14.48 GB、14.06 KB)和(161.78 MB、92.45 MB、13.60 KB),构造方案的公钥长度、私钥长度、密文长度分别为(117.79 MB、67.31 MB、10.15 KB),比其他IND-CCA安全方案更高效。除此之外,在相同安全参数情况下,构造方案的解码错误率是2-Θ(k2),比其他IND-CCA安全方案的解码错误率更低。
