融合特征自适应抑制式模糊聚类彩色图像分割
2021-03-14韩天玥
兰 蓉,韩天玥
(西安邮电大学 通信与信息工程学院,陕西 西安 710121)
图像分割的目的是根据灰度、颜色或纹理等特征将图像划分成若干区域[1],被广泛应用于图像压缩[2]、网络视频传输[3]、医学图像诊断[4]和目标跟踪[5]等领域的图像处理过程中。图像分割结果直接影响后续图像处理的效果。
图像分割一般通过提取图像特征并结合不同策略进行[6-8]。现有的图像分割方法通常通过采用多种提取方式以获得多维图像特征,例如,基于区域的彩色图像分割(Region-based Color Image Segmentation,RCIS)算法[9]、基于特征融合视觉显著性的图像分割算法[10]、基于多尺度颜色特征和小波纹理特征(Multiscale Color and Wavelet-based Textures,MCWT)的无监督火焰图像分割算法[11]等。这些算法同时考虑图像色彩和纹理特征,避免了传统算法将彩色图像转换为灰度图像时损失颜色及细节信息的问题,但是在分割精度上仍有待进一步提高。
影响彩色图像分割精度的因素,除了图像特征提取方式,还有图像的分割策略。文献[12]提出的抑制式模糊C-均值(Suppressed Fuzzy C-Means,SFCM)聚类是一种进行彩色图像分割的有效方式,但是,SFCM算法采用固定值0.5作为抑制因子,在一定程度上影响算法的适应性。事实上,在图像分割的过程中,若能够根据图像自身特性自适应地选取抑制因子值[13],则会使得算法在保持分割精度的同时,还可以获得较快的收敛速度[14-16]。文献[17]给出抑制因子的柯西型指数选择公式,提升了收敛速度,但是,该算法对初始聚类中心较为敏感,在一定程度上影响算法运行效率。文献[18]结合像素空间信息,通过在聚类过程中动态设置抑制因子来提高分割精度,但该算法相比SFCM算法的运行速度有所减慢。
为了提高彩色图像分割精度,本文拟在SFCM算法的基础上提出一种融合特征自适应抑制式模糊聚类彩色图像分割 (Adaptive Suppressed Fuzzy Clustering Color Image Segmentation with Fused Features,FFA-SFCM)算法。首先,在Lab空间提取图像颜色信息,并对彩色图像进行块划分,采用Haar小波变换提取各图像块的纹理特征,结合半方差函数描述图像空间信息,得到图像的颜色与纹理融合特征。其次,对每一个样本计算其非最大隶属度均值作为该样本的抑制因子,以动态地获得抑制因子值。最后,针对SFCM聚类算法对初始聚类中心敏感,迭代时间较长等问题,利用自适应带宽参数改进均值漂移聚类(Mean-Shift-Cluster)算法[19-20],得到SFCM算法初始聚类中心和聚类数目,以加快SFCM算法收敛速度,提高图像分割精度。
1 预备知识
1.1 抑制式模糊C-均值聚类算法
模糊C-均值(Fuzzy C-Means,FCM)[21]聚类算法利用模糊集理论构建目标函数,其目标函数为
(1)
其中:m为模糊因子,通常取2;uij表征样本xi(i=1,2,…,n)到聚类中心vj(j=1,2,…,c)的隶属度;dij为样本xi到聚类中心vj的欧式距离;uij∈[0,1],且满足条件
利用拉格朗日乘数法求解式(1),即可得到隶属度uij和聚类中心vj,其计算表达式分别为
(2)
(3)
为提高FCM聚类算法迭代速度并保持良好聚类效果,Fan[12]等提出SFCM聚类算法,采用“竞争学习”的思想,通过抑制因子α修正uij。
设第样本p具有最大隶属度,即


其中,抑制因子α∈[0,1]。
SFCM算法的初始聚类数目需事先设定,且随机确定初始聚类中心,容易造成聚类结果陷入局部最优,算法收敛速度慢等问题。
1.2 Mean-Shift聚类算法
Mean-Shift算法[19-20]是一种核密度估计算法,其核心是对特征空间的样本进行聚类,得到密度梯度为0的模式点。
设zi(i=1,2,…,n)为d维空间Zd中的样本,则在任意点的Mean-Shift量为
(4)
其中:B={y:(y-z)′(y-z)≤k}表示半径为k的高维球区域;l表示在n个样本点中,位于B区域的样本数。
式(4)可以表述为
M(z)=msh(z)-z
当给定初始样本点z、带宽参数k(即高维球区域的半径)以及容许误差ε,Mean-Shift算法采用如下的选代过程。
步骤1计算msh(z)。
步骤2计算dist=‖msh(z)-z‖。
步骤3若dist<ε,则终止循环,将msh(z)即为一个模式点;若dist≥ε,则令z=msh(z)继续执行步骤1。
2 FFA-SFCM算法
为了提高彩色图像分割准确率,加快SFCM算法收敛速度,提出FFA-SFCM算法。使用颜色、纹理融合特征表示彩色图像,利用模糊隶属度构造SFCM算法的抑制因子自适应选取公式,针对SFCM聚类算法对初始聚类中心敏感的问题,利用改进的自适应均值漂移聚类(Mean-Shift-Cluster)算法优选初始聚类中心,加快算法收敛。
2.1 颜色与纹理融合特征的提取
2.1.1 颜色特征的提取
选取合适的颜色空间是有效分割彩色图像的基础。常见的红绿蓝(Red Green Blue,RGB)颜色空间将所有的颜色看作3个基色的组合,其R、G、B分量之间存在较强的相关性,不适用于3个分量独立运算的彩色图像分割中。为此,采用Lab颜色空间[22]提取图像的颜色特征。Lab空间中的分量L表示亮度信息,分量a、b反映色彩信息。其中,分量a表示从红色到绿色范围的颜色信息,分量b表示从黄色到蓝色范围的颜色信息。Lab空间的3个分量之间不存在强的相关性,另外,Lab颜色空间具有欧式距离不变性,即视觉上差异较小的两种颜色在Lab颜色空间的欧式距离也较小,提取出的颜色特征接近人眼的视觉感受,适用于彩色图像分割[22]。
将原始彩色图像由RGB颜色空间转化到Lab颜色空间的计算表达式[22]为
(5)
(6)
其中:w1、w2、w3为中间量;R、G、B分别表示图像在RGB颜色空间的红、绿、蓝分量值;函数
2.1.2 小波纹理特征提取
小波变换是对信号进行多尺度分析的有力工具[23],为保证计算速度和特征提取的有效性,采用Haar小波对图像进行小波分解。
由于分块提取特征能够得到更丰富的图像细节信息,因此,首先以s1×s2大小对图像进行划分。经过二维Haar小波分解得到原始图像的近似值及其水平、垂直和对角方向的细节信息。由于小波细节图像为原图各个频道的能量分布,包含了不同方向上的纹理信息,提取细节子图的熵作为纹理特征[24],则图像第i个像素点对应的小波纹理特征可表示为(TLH,i,THL,i,THH,i),其中,TLH,i、THL,i和THH,i分别表示第i个像素所在图像块经小波分解后得到的水平、垂直和对角线分量。
2.1.3 纹理特征的提取
采用半方差函数提取图像的纹理特征。半方差函数γ(h)代表空间相距为h的像素对差值二次增量的数学期望的一半,其取值依赖于两个样本间的空间距离h的大小和角度[25],γ(h)从统计角度衡量数据的局部变化与空间相关性,能够反映图像的纹理特征[25]。半方差函数的定义为
其中:E(·)为期望值;d(xi)代表图像像素点i处的灰度值;h取值由图像的大小决定。
设图像共含n个像素,提取各像素点Lab颜色空间的分量作为其颜色特征,(Li,ai,bi)表示第i(i=1,2,…,n)个像素点在Lab颜色空间的坐标。对各图像块提取半方差图特征,将图像第i个像素点对应的半方差图特征表示为Si,则可以将原图中像素点i对应的特征向量表示为
Gi=(Li,ai,bi,TLH,iTHL,i,THH,iSi)
(7)
2.2 初始聚类中心的选择
SFCM算法需要事先设定初始聚类数目,随机确定初始聚类中心,聚类结果可能陷入局部最优,并且算法收敛速度较慢,为此,利用改进的Mean-Shift算法获得数据集的聚类数目和聚类中心,并将其作为SFCM聚类算法的初始值。
在Mean-Shift算法中,带宽参数k的选择至关重要,选择较小的带宽会导致算法收敛速度较慢;选择的带宽较大,虽然会加速算法收敛速度,但是,有可能影响最终聚类的效果。为此,采用一种基于类别方差的带宽自适应方式来改进Mean-Shift算法。改进算法采用如下步骤。
设图像的像素个数为n,将像素点i的特征向量Gi重写为Xi=[xi1,xi2,…,xi7],i∈{1,2,…,n}。


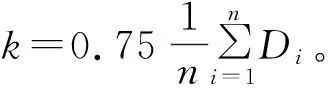
2.3 抑制因子的自适应选取
SFCM算法中的抑制因子α的取值固定,在一定程度上影响了算法的适应性,为此,采用一种自适应选取抑制因子的方式,动态地获得抑制因子值,使得隶属度能够根据变化进行修正,在保证聚类精度的同时提高算法的收敛速度。
设样本点xi(i=1,2,…,n)的隶属度为uij(i=1,2,…,n;j=1,2,…,c),其中,xi对于各类的最大隶属度为uip,则样本点xi的抑制因子为
(8)
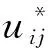
(9)
(10)
样本最大隶属度uip越大,表明样本距离最大隶属度所在的第p类距离越近,此时样本对该类别具有竞争优势,应予以奖励,同时,对样本到其他类的隶属度uij(j≠p)进行抑制[14]。当样本最大隶属度越大时,其非最大隶属度之和越小,则抑制因子αi越小,对非最大隶属度所在类的抑制程度越大,从而对最大隶属度的奖励就越大。这种抑制方式满足SFCM算法“竞争学习”机制的基本原理。
设计的自适应生成抑制因子的方式进一步强化了最大隶属度奖励机制,可以加快算法收敛。此外,由式(8)获得的αi值随迭代过程中隶属度随uij的变化而变化,即能够根据模糊划分的矩阵实现抑制因子的动态调整,使得样本能够更加高效地实现类别归属,改善聚类效率。
2.4 算法实现步骤
FFA-SFCM算法采用如下步骤实现。
步骤1将图像转换至Lab颜色空间,根据式(5)和式(6)提取图像颜色特征。
步骤2根据图像半方差图特征与二维小波变换结果,提取图像纹理特征,得到图像的7维融合特征。
步骤3确定Mean-Shift带宽参数,并通过Mean-Shift聚类获得聚类中心与类别数目。
步骤4使用SFCM算法对获得的聚类中心与类别数目进行聚类并初始化其余参数,设置迭代次数g,迭代终止阈值σ,最大迭代次数T,模糊指数m。
步骤5利用式(2)计算隶属度函数uij,利用式(8)动态获取抑制因子αi,并利用式(9)与式(10)修正隶属度函数。
步骤6利用式(3)迭代计算聚类中心。若‖vg+1-vg‖<σ或迭代次数g>T,则停止循环迭代,否则,令g=g+1并返回步骤5。
3 实验结果与分析
为验证FFA-SFCM算法的性能,从彩色图像数据集CALTECH 101、Berkeley Segmentation Data Set (BSDS) 500以及Google Earth遥感图像中选择若干图像进行测试。
将提出的FFA-SFCM算法与基于区域的快速图像分割算法[7](Fast Region-based Image Segmentation Algorithm,FRISA)、自适应彩色图像分割算法[8](Adaptive Color Image Segmentation Algorithm,ACISA),RCIS算法[9],MCWT算法[11],FCM算法[21]、SFCM算法[12]以及改进的抑制模糊C-均值(Improved Suppressed Fuzzy C-Means,IS-FCM)算法[18]在分割效果和分割指标两个方面进行对比与分析,检验本文算法的性能。其中:FRISA算法提取图像颜色纹理等融合特征,并利用改进的K均值算法进行聚类分割;ACISA算法提取小波纹理等特征组成特征向量,采用改进的KFCM聚类算法实现图像分割;IS-FCM算法根据样本到聚类中心的最大和最小距离动态设定抑制因子,对FCM算法进行了改进。
实验在2.3 GHz CPU、四核Intel Core i5、8 GB内存、macOS Catalina环境下进行,软件仿真利用Matlab R2018a实现。实验中设置参数s1=4,s2=4,h=2,ε=1.5,σ=1×10-5,T=100,m=2。
采用划分系数(Partition Coefficient,PC)[26]与划分熵(Partition Entropy,PE)[27]作为聚类有效性评价指标。PC和PE能够反映划分矩阵的模糊程度,PC值越大,划分矩阵的模糊性越小,聚类性能越好;PE值越小,样本分类越准确。
对于图像分割性能,选择分割准确率(Segmentation Accuracy,SA)[28]、规范化互信息(Normalized Mutual Information,NMI)[29]和结构相似性(Structural Similarity Index,SSIM)[30]作为评价指标。SA和NMI的值越大,表明分割结果越接近标准分割。SSIM越接近1,表明算法实际分割结果与标准分割结果之间的相似性越大。
另外,为了验证算法失真性能,引入分割结果与原图的峰值信噪比(Peak Signal to Noise Ratio,PSNR)[31]作为算法的评价指标。PSNR值越大,说明图像失真越少。
3.1 算法的有效性
选取CALTECH 101数据库中覆盖所有类别的1 010幅图像、BSDS500图像库中全部506幅图像以及50幅随机截取的Google Earth遥感图像作为实验对象,分别使用改进的Mean-Shift和随机方式选取初始聚类中心,测试其平均迭代次数和平均收敛时间两个反映技术效率的指标,两种方式选取初始聚类中心的效率如表1所示。为验证提出的自适应抑制因子选取方式的有效性,测试抑制因子取固定值0.5、IS-FCM和改进算法等3种抑制因子确定方式的平均迭代次数与平均收敛时间等效率指标,实验结果如表2所示。
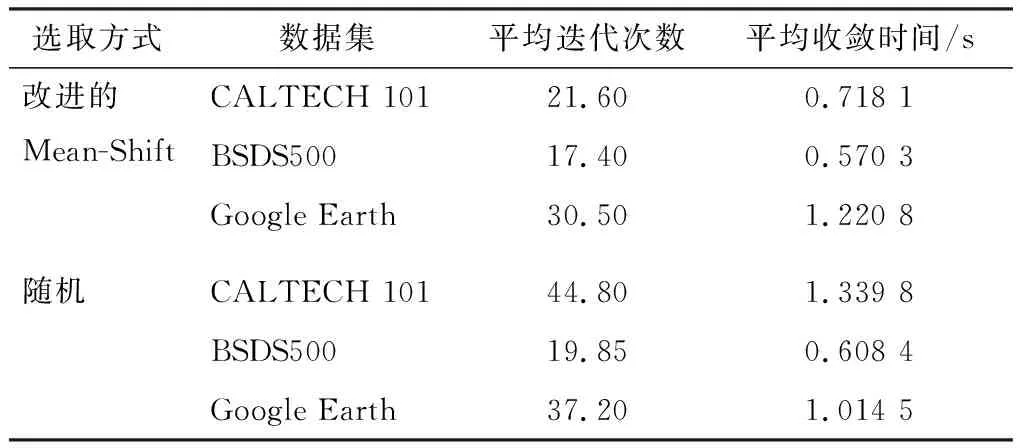
表1 两种方式选取初始聚类中心的效率

表2 不同抑制因子确定方式的效率
从表1可以看出,使用改进的Mean-Shift方法选择初始聚类中心可以有效减少算法迭代次数,缩短算法收敛时间。这是因为,随机选取的初始聚类中心具有不确定性,会在一定程度上影响SFCM算法的聚类分割效率,而改进算法选择的初始聚类中心根据图像自身特征确定,可以提高SFCM算法聚类效率。
从表2可以看出,改进算法的抑制因子自适应确定方式的迭代次数和运行时间较少,算法效率较高。
为了分析提取不同特征对图像分割效果的影响,分别选取BSDS500图像库中#3063和#253036两幅图像、CALTECH 101数据库中#0048和#0071两幅图像以及Google Earth遥感图像#001和#002两幅图像作为实验对象,分别提取各图像在Lab颜色空间的3维颜色特征、结合小波纹理特征组成的6维颜色纹理特征以及结合半方差图特征的7维融合特征进行实验,测试各图像分割结果的划分熵、划分系数以及图像的分割准确率,分割量化指标如表3所示。可以看出,改进算法提取7维融合特征表征的图像分割结果的性能指标更优,这是因为,提取的7维融合特征不仅包括图像的颜色特征,还包括描述图像细节信息的小波纹理特征和描述图像空间信息的半方差图特征,三者结合后对图像的描述更为细致和全面,以其作为图像分割的依据,分割结果会更为准确。

表3 提取不同特征表征图像信息的分割量化指标
3.2 算法的可视化效果
选取CALTECH 101图像库中#0048、#0063和#0071图像进行实验,原始图像如图1所示。选择的3幅图像的前景内容均为单个物体,便于通过视觉观察图像分割结果。8种算法对3幅图像的分割结果分别如图2、图3和图4所示。

图1 CALTECH 101图像库中的原始测试图像
图2显示,MCWT算法不能有效区分花蕊与花瓣;FRISA与ACISA算法的分割结果均未能得到完整的花蕊;RCIS算法对花瓣的分割效果不理想;SFCM算法和FCM算法均未能准确分割花瓣右上角区域与天空背景;而改进算法能够较为准确地分割花瓣与花蕊,天空与大地。这是因为,改进算法利用图像小波分解提取到图像水平、垂直以及对角方向等更加详细的细节信息,能够对图像的细节部分进行更为准确的分割。

图2 8种算法对#0048图像的分割结果
图3显示,RCIS算法未能准确判别海星基本轮廓,MCWT、FRISA、SFCM、FCM、ACISA和IS-FCM算法均不能有效抑制背景沙滩部分的噪声,相比之下,改进算法对背景噪声的抑制较为有效,分割结果更为准确。

图3 8种算法对#0063图像的分割结果
图4显示,MCWT、FRISA、RCIS、SFCM和FCM算法均对背景的沙滩四角区域产生误判;IS-FCM与ACISA算法的分割结果均缺失了海星的一角;而FFA-SFCM算法能有效地区分海星与背景的沙滩,更完整地保留了海星轮廓。

图4 8种算法对#0071图像的分割结果
CALTECH 101图像库没有提供标准分割图像,而BSDS500图像库包含由专家手工标注的标准分割图像,是经常被用作测试图像分割性能的数据集[15],为此,选取BSDS500图像库中的#3063、#3096、#135069等3幅图像进行实验。3幅原始测试图像如图5所示,标准分割图像如图6所示。8种算法对3幅图像的分割结果分别如图7、图8和图9所示。可以看出,与其他算法相比,改进算法FFA-SFCM可以更加有效地区分目标与背景。

图5 BSDS500图像库中的原始测试图像

图6 BSDS500图像库中测试图像的标准分割图像

图7 8种算法对#3063图像的分割结果

图8 8种算法对#3096图像的分割结果

图9 8种算法对#135069图像的分割结果
为了进一步测试算法在纹理信息较为丰富的彩色图像上的分割效果,选取Google Earth数据库中的#001、#002和#003等3幅遥感图像进行实验。遥感图像更为复杂,包含更多的纹理信息和干扰,能够进一步测试算法的图像分割性能。原始遥感测试图像如图10所示。8种算法对3幅遥感图像的分割结果分别如图11、图12和图13所示。可以看出,改进算法能更准确地划分房屋、庄稼与绿地区域,保持较丰富的细节信息。这是因为在描述彩色图像时,改进算法提取了图像的纹理特征作为聚类分割的样本,因此,相比其他对比算法,能更准确地分割纹理特征较为复杂的遥感图像。

图10 Google Earth库中的原始测试图像

图11 8种算法对#001图像的分割结果

图12 8种算法对#002图像的分割结果

图13 8种算法对#003图像的分割结果
3.3 图像分割的量化性能
为分析本文算法聚类性能,选取CALTECH 101图像库中#0048、#0063和#0071图像进行测试。表4给出了8种算法在划分熵和划分系数指标上的统计结果。可以看出,改进算法的划分熵与划分系数指标均优于其他对比算法,这是因为,改进算法采用抑制因子自适应选择方式,加强了SFCM算法对最大隶属度的奖励,使得其具有较好的聚类性能。

表4 8种算法对CALTECH 101数据库部分图像的分割量化结果
由于CALTECH 101图像库没有提供标准分割图像,无法客观评价分割准确率,为进一步分析改进算法的图像分割性能,选取BSDS500图像库中的#3063、#3096和#135069等3幅图像进行测试。8种算法的划分熵、划分系数、分割准确率、互信息指数、结构相似度和峰值信噪比等6个性能指标数据如表5所示。可以看出,相较于对比算法,改进算法能够获得较好的聚类性能。这是因为,FCM和SFCM算法仅使用灰度信息分割图像,RCIS、MWCT、ACISA和FIRSA算法提取的图像特征的维数较少,而改进算法采用多维度的融合特征来表征图像,上改善了图像分割效果。另外,相比IS-FCM算法,改进算法的抑制因子自适应方式较佳,因而能够获得更高的分割准确率。

表5 8种算法对BSDS500数据库测试图像分割的量化指标
为了测试算法在富含纹理信息图像上的性能指标,选取部分Google Earth数据库中的#001、#002和#003等3幅遥感图像进行测试。表6给出了8种算法的划分熵、划分系数和峰值信噪比3个指标数据。表6显示,改进算法的聚类性能和峰值信噪比指标均优于对比算法,说明改进算法在分割纹理信息较为丰富图像的效果较好。

表6 8种算法对Google Map数据库测试图像分割的量化指标
4 结语
针对抑制式模糊C-均值聚类算法对初始聚类中心敏感和抑制因子无法自适应选择导致分割精度、效率较低等问题,提出了一种融合特征自适应抑制式模糊聚类彩色图像分割算法。在颜色特征基础上,结合小波变换和半方差函数得到颜色与纹理融合特征以更好地概括图像信息。在对图像进行聚类分割之前,利用改进的Mean-Shift算法确定了初始聚类中心与聚类数目,并根据模糊隶属度构造出SFCM算法的抑制因子自适应选取公式,实现了抑制因子的动态调整。仿真实验表明,相较于相关经典算法,改进算法提取的融合特征能够更加有效地描述图像信息,图像的分割精度较高,在视觉效果和评价指标方面均有较好的结果。此外,通过优选初始聚类中心、聚类数目和抑制因子自适应选择方式,加快了算法收敛速度,提高了算法的执行效率。
