基于改进阈值函数的手指静脉图像增强算法

张雪锋，董芸嘉，姜 文

(1.西安邮电大学 网络空间安全学院，陕西 西安 710121;2.国家计算机网络应急技术处理协调中心，北京 100029)

生物特征识别技术[1]是通过生物自身所具备的特征识别个体，具有唯一性、不易变更和便于携带等特性，已成为身份识别技术[2]的主要方法之一。手指静脉识别技术作为一种新兴的生物特征识别技术，基于人类静脉血管中流动的血液可吸收特定波长光线的原理[3]，利用近红外光照获得手指静脉的生物特征信息，通过对比生物特征信息实现识别，具备高安全性、高识别精度和识别速度快等优势。在手指静脉识别过程中，手指静脉图像的质量对后续的特征提取和匹配识别的准确率有着直接的影响。因此，手指静脉图像增强在手指静脉识别过程中尤为重要[4]。

近红外线透过手指读取的图像，经转换和传输后或因其本身受光不均等因素，难免产生模糊、目标和背景对比度不明显以及噪声较大等问题。因此，在图像预处理过程中需对图像进行增强并且减少噪声处理。当使用传统的图像增强方法，如直方图均衡化[5]对手指静脉图像进行处理时，利用将中间灰度向高灰度与低灰度两端伸展，增大像素灰度级的动态分布范围的方法，虽然增加了对比度，且降低了算法复杂度，但易丢失图像的细节信息，使得图像信息不完整。基于脊波变换的静脉图像增强算法[6]的实质是由增益函数根据脊波大小进行自适应调整，再由增强变换后的系数重构得到增强后的图像，其在处理静脉图像点奇异性方面效果并不理想。反锐化掩膜法[7]通过增强静脉轮廓达到增强的目的，但其在处理过程中对噪声极其敏感，导致噪声加大、细节丢失及图像质量降低。文献[8]提出了一种对比度自适应直方图均衡化的方法对手掌静脉和手指静脉进行图像增强处理，虽然增强了手指静脉血管的纹理特征和图像整体对比度，但是去噪效果并不理想。因此，基于频域拟提出一种基于改进阈值函数的手指静脉图像增强算法。先将手指静脉图像进行二维小波变换，对低频子带系数进行非线性增强，对高频子带系数进行有限脊波变换，利用改进阈值函数对脊波系数进行处理，然后在小波域对图像进行重构，得到增强后的手指静脉图像，以期在频域上有较好的图像增强效果。

1 理论基础

1.1 小波变换

小波变换继承和发展了短时傅里叶变换局部化思想，同时又克服了窗口大小不随频率变化等缺点，能够提供一个随频率改变的“时间-频率”窗口。具体变换是由一个平方可积分函数f(t)与一个在时频域上均具有良好局部性质的小波函数ψ(t)的内积，其数学表达式[9]为

(1)

其中：a>0为尺度因子；b为位移因子；t为时间；*表示复数共轭。

根据图像的自身特点，将小波变换应用到图像处理中时，需将小波变换从一维推广到二维。因此，对一幅大小为M×M的手指静脉图像进行一层小波分解，得到大小为M/2×M/2的4个子带图像，分别为低频子带和水平、垂直、斜方向的高频子带。低频子带包括了图像主要的轮廓信息，高频子带包含了噪声和细节。

1.2 脊波变换

脊波变换是一种非自适应的高维函数表示方法，其核心主要是先利用Radon变换[10]把线状奇异性变换为点状奇异性，然后通过小波变换处理在Radon域的点状奇异性。静脉图像含有二维曲线奇异分析和方向选择要求，而脊波变换是Radon域上的一维小波变换，在处理线性，特别是直线型奇异性时表现了良好的性能，能够克服小波变换在高维曲线奇异性和方向选择上的不足。脊波变化的实质是添加一个表征方向的参数给小波基函数，其不仅在表征图像现行奇异边缘方面具有优越性，还具有局部时频分析的能力。

(2)

其中：c、d和θ分别为脊波的尺度、位置和方向参数；x=(x1,x2)表示具有高维奇异性特征的信号。φc,d,θ存在逆变换，式(2)表明脊波函数在直线x1sinθ+x2cosθ=e方向上是连续的，e为常数。

2 手指静脉图像增强算法

基于改进阈值函数的手指静脉图像增强算法先将手指静脉图像进行二维小波变换，得到低频子带系数和高频子带系数。对低频子带系数进行非线性增强，对高频子带系数进行有限脊波变换，利用改进阈值函数对脊波系数进行处理，最后，将处理后的低频子带系数和高频子带系数在小波域进行小波逆变换得到增强后的图像。具体步骤如下。

步骤1对手指静脉图像进行二维小波变换，由式(1)得到低频子带系数和高频子带系数。

步骤2采用非线性增强系数对低频子带系数进行处理，保留图像的轮廓信息。

步骤3对高频子带系数进行脊波变换，利用式(2)得到脊波系数，通过改进阈值函数在脊波域处理脊波系数，最后通过脊波逆变换到小波域。

步骤4对处理后的低频子带系数和高频子带系数在小波域进行小波重构，得到重构的增强图像。

2.1 低频子带系数非线性增强

对图像增强来说，理想的小波基应具有正交性、紧支性与衰减性、对称性、正则性和消失矩等5个特性。dbN小波[12]具有较好的正则性，即该小波作为稀疏基所引入的光滑误差不容易被察觉，使得信号重构过程比较光滑。dbN小波的特点是随着阶次(序列N)的增大消失矩阶数越大，其中，消失矩越高光滑性就越好，频域的局部化能力就越强，频带的划分效果越好，但是会使时域紧支撑性减弱，同时计算量增加，实时性变差。因此，基于改进阈值函数的手指静脉图像增强算法选择小波基为“db8”的小波变换将手指静脉图像分解为1个低频子带和3个高频子带，即低频子带、水平方向的高频子带、垂直方向的高频子带以及斜方向的高频子带。低频子带主要包含图像的轮廓信息，为了使处理后的手指静脉图像轮廓信息较为明显，并保持原始的信息量，对得到的低频子带系数进行非线性增强处理。

2.1.1 低频子带系数阈值的确定

步骤1估计噪声方差。采用稳健均值[13]对小波变换后的斜方向高频子带系数估计，得到噪声方差为

(3)

其中：Median是中值函数；gH(m,n)是小波变换后的斜方向高频子带系数，m和n分别表示子带系数矩阵的行向量和列向量。

步骤2计算低频子带的方差

(4)

其中：R·R是图像经小波变换后低频子带的尺寸；gL(m,n)是小波变换后得到的低频子带系数。

步骤3计算低频子带系数相应的新阈值

(5)

2.1.2 非线性增强系数

对小波变换后的低频子带系数进行非线性增强系数处理，定义非线性增强系数的公式为

(6)

其中,0≤α≤1。非线性增强系数以0.8δL和δL为分界点，分3个部分估计低频子带系数，示意图如图1所示。

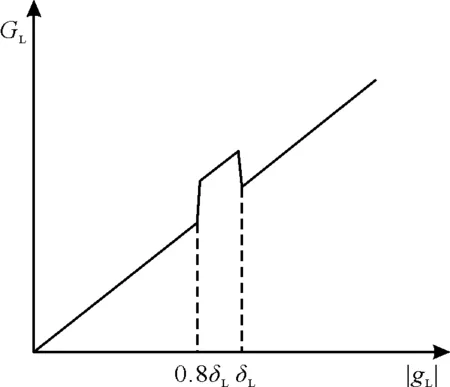
图1 非线性增强系数示意图

由式(6)和图1可知，当|gL|≤0.8δL或|gL|>δL时，GL保持不变，尽可能保留了原有的有效信息量不变。当0.8δL<|gL|≤δL时，通过式(6)有效地提升了低频子带系数，从而增强图像的轮廓信息。

2.2 高频子带系数处理

图像的高频子带系数主要是图像的局部信息，即图像的边缘、细节和噪声等3部分。先对水平方向的高频子带系数、垂直方向的高频子带系数和斜方向的高频子带系数进行有限脊波变换，得到脊波系数，再在脊波域建立改进的阈值函数，利用改进阈值处理脊波系数。最后，在脊波域对脊波系数进行逆变换到小波域，得到处理后的高频子带系数，从而更好地分离噪声分量，减少阈值函数的恒定偏差，保留图像的细节信息。

2.2.1 高频子带系数阈值的确定

3个高频子带系数的噪声不相同，因此在不同的的子带上应采用不同的脊波阈值。3个高频子带经脊波变换后的脊波系数阈值确定的具体步骤如下。

步骤2计算高频子带系数经脊波变换后的脊波系数噪声方差

(7)

其中：J·K是高频子带系数经脊波变换后的尺寸；hi(j,k)表示高频子带系数经脊波变换后脊波系数，i=1,2,3，j和k分别表示高频子带系数经脊波变换后的矩阵行向量和列向量。

步骤3计算每个高频子带相应的阈值为

(8)

2.2.2 改进阈值函数

新的脊波系数是由脊波系数通过改进阈值函数处理得到。针对传统软硬阈值函数造成恒定偏差以及模糊失真等问题，定义改进阈值函数为

(9)

其中，β=1-exp[-u(|hi|-δi)]，0≤u≤10是自适应系数，通过u调整β的大小。

改进的阈值函数以δi、0.65max|hi|和max|hi|为分界点，分3个部分对脊波系数进行处理，改进的阈值函数示意图如图2所示。

图2 改进的阈值函数示意图

由式(9)和图2可知，当|hi|≤δi时，GH=0，能够有效去除噪声。当δi<|hi|≤0.65max|hi|时，GH为hi与β倍的δi的差值，能够减小hi大于δi的恒定误差，并且能够通过改变u的大小得到不同的β，有较好地适应性。当0.65max|hi|<δi≤max|hi|时，保持hi不变，能够保留图像的细节信息。

3 实验仿真及分析

在操作系统为Windows 10，处理器为Intel(R) Core(TM)I5-4200U CPU @2.30 GHz，内存为4.00 GB的计算机上，采用Matlab R2016b 仿真软件进行仿真实验，验证分析基于改进阈值函数图像增强算法的图像增强效果和图像去噪效果。

3.1 图像增强效果分析

为了验证基于改进阈值函数图像增强算法对手指静脉图像的增强效果，选取尺寸为328×328的手指静脉图像，分别利用基于小波变换的自适应图像增强算法[14](简称文献[14]算法)、直方图均衡法、直方图均衡和小波去噪相结合的图像增强算法[15](简称文献[15]算法)、基于脊波变换的图像增强算法[16](简称文献[16]算法)、基于阈值函数的图像增强算法[17](简称文献[17]阈值算法)、基于改进阈值函数的图像去噪算法[18](简称文献[18]算法)、基于小波变换和改进中值滤波的算法[19](简称文献[19]算法)和所提算法进行图像增强，结果如图3所示。

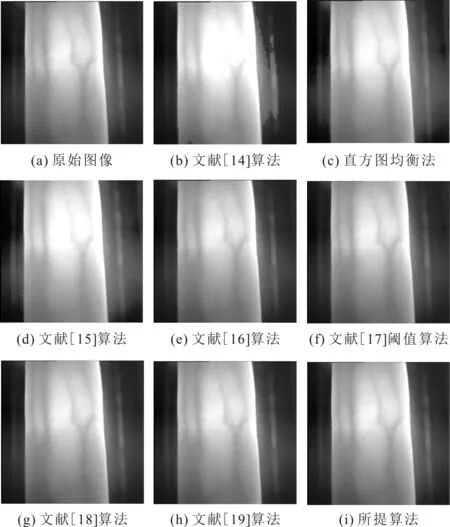
图3 不同算法的图像增强结果

由图3(b)、图3(c)和图3(d)可以看出，当使用基于小波增强的图像增强算法和直方图均衡法时，得到的手指静脉图像的边缘和细节信息会丢失，并且增强后的图像对比度不自然。而由图3(e)、图3(f)、图3(g)、图3(h)和图3(i)可以看出，当使用基于脊波变换的图像增强算法、各种基于阈值函数的小波去噪方法以及所提算法增强后的图像，整体视觉效果较好，能够保留图像的细节信息。

根据信噪比、峰值信噪比、结构相似度、信息熵和平均梯度等客观评价指标对图像增强效果进行评价。信噪比数值越大，说明混在信号里的噪声越小。峰值信噪比数值越大表示失真越小。结构相似度一种衡量两幅图像相似度的指标，数值越大与原图的相似性越高。信息熵是指图像的平均信息量，从信息论的角度衡量图像中信息的多少，信息熵越大，说明图像包含的信息越多。平均梯度是手指静脉图像细节表达能力以及纹理特征的一种指标，数值越大，表示图像层次越多，图像的清晰度越高。不同算法的图像增强效果对比如表1所示。

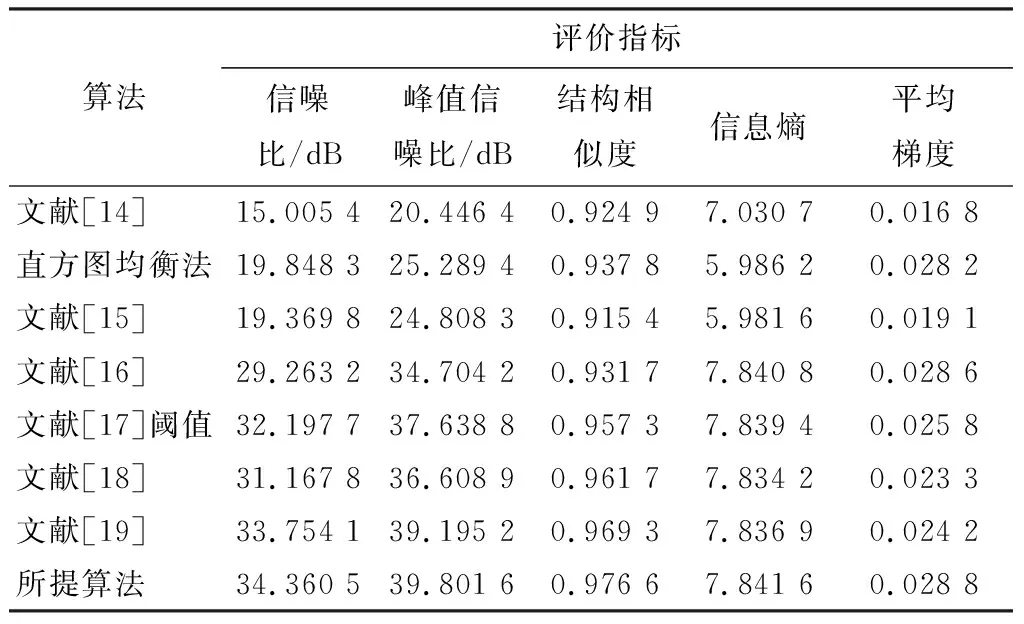
表1 不同算法的图像增强效果对比

由表1可以看出，所提算法的信噪比、峰值信噪比、结构相似度、信息熵和平均梯度均高于其他算法，说明采用所提算法处理手指静脉图像，保存了图像的细节信息，减少失真，而且去噪能力也有所增强，使得图像质量得到了明显的提高。

3.2 图像去噪效果评价

采用峰值信噪比评价去噪性能。对实验图像分别加入不同的噪声，对比不同算法的去噪性能。

对实验图像加入信噪比为40 dB的加性高斯白噪声，不同算法的去噪效果如图4所示。

图4 加入加性高斯白噪声后不同算法的去噪效果

由图4可以看出，当对手指静脉图像加入加性高斯白噪声时，文献[16]算法去噪效果不理想，还存在明显的噪声，这是由于该算法对小波变换后的高频子带进行了脊波变换，利用非线性增强系数对脊波系数进行了处理。而所提算法和其他3种算法处理加噪图像没有明显噪声，去噪效果较好，更好地保留了图像的细节信息。

加入加性高斯白噪声后，文献[16]算法、文献[17]阈值算法、文献[18]算法、文献[19]算法和所提算法的峰值信噪比分别为27.429 5 dB、36.593 5 dB、36.702 0 dB、36.201 8 dB和37.941 4 dB。可以看出，所提算法的峰值信噪比均比其他算法高，说明所提算法去除噪声效果好，且失真较小。

对实验图像加入噪声密度为0.01的椒盐噪声，不同算法的去噪效果如图5所示。

图5 加入椒盐噪声后不同算法的去噪效果

加入不同噪声密度的椒盐噪声，不同算法的峰值信噪比对比如表2所示。

表2 加入椒盐噪声后不同算法的峰值信噪比对比

由图5与表2可知，对于加入相同噪声密度的椒盐噪声，所提算法采用改进阈值函数对加噪图像的去噪效果优于其他算法。文献[17]阈值算法的峰值信噪比仅次于所提算法，说明所提算法在频域上有较好的去噪效果。

对实验图像加入由数据生成的泊松噪声，不同算法的去噪效果如图6所示。

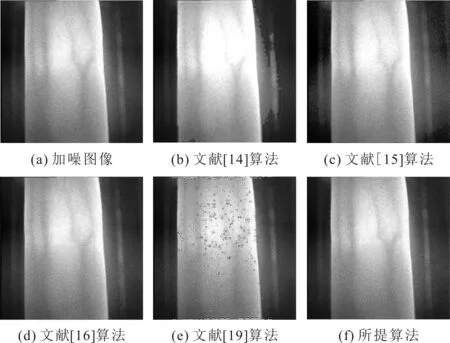
图6 加入泊松噪声后不同算法的去噪效果

由图6可以看出，对加入泊松噪声的手指静脉图像采用文献[14]算法和文献[15]算法处理后，图像对比度不自然，视觉效果差。采用文献[19]算法处理后，有明显噪声放大现象。而采用文献[16]和所提算法处理加噪手指静脉图像后没有明显噪声，去噪效果较好。

加入泊松噪声后，文献[14]算法、文献[15]算法、文献[16]算法、文献[19]算法和所提算法的峰值信噪比分别为20.374 6 dB、23.369 8 dB、26.534 2 dB、19.223 5 dB和27.604 2 dB。所提算法和文献[16]算法的峰值信噪比高于其他算法，图像去噪效果较好。

对图像加入方差为0.01的乘性噪声图像，不同算法的去噪效果如图7所示。

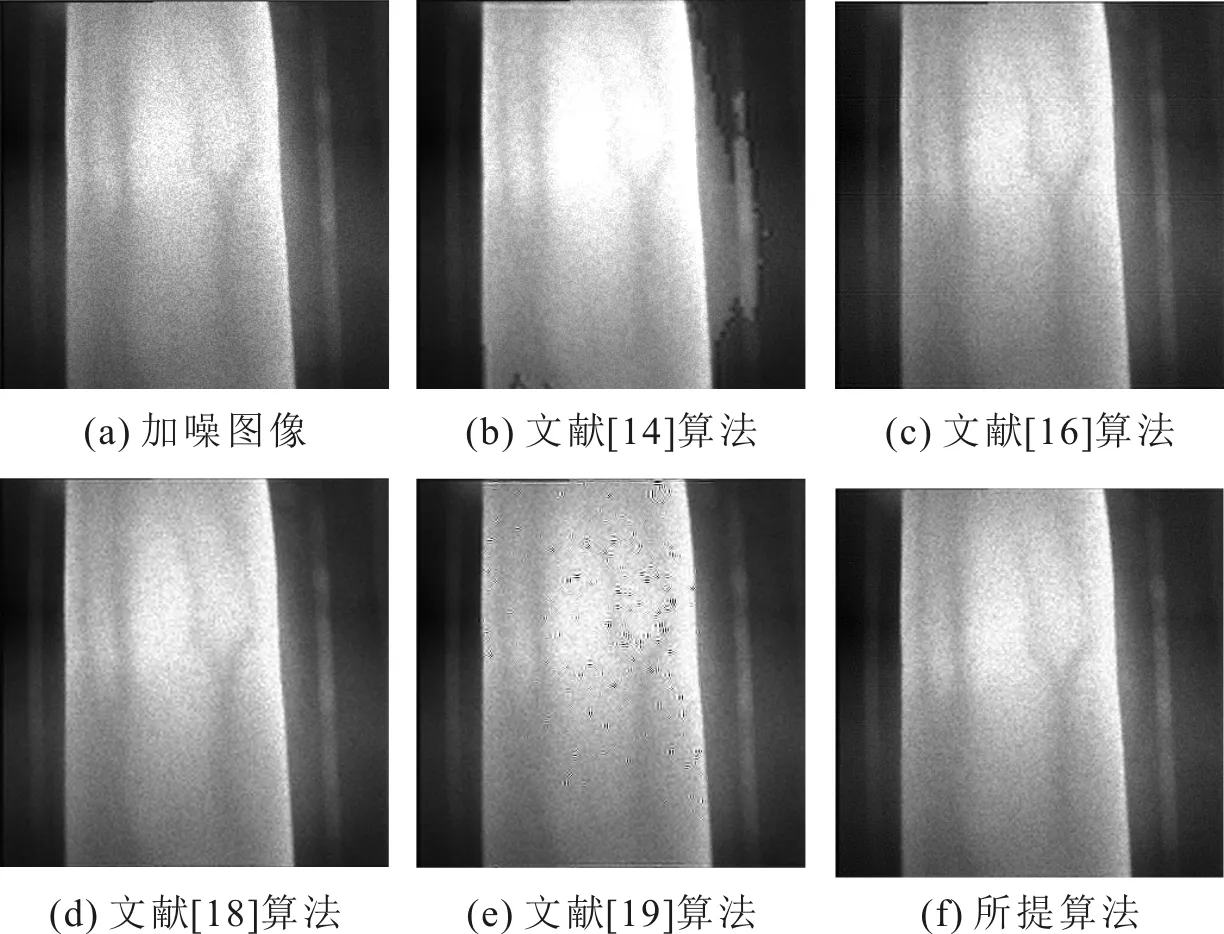
图7 加入方差为0.01乘性噪声后不同算法的去噪效果

由图7可知，当加入方差为0.01的乘性噪声时，文献[14]算法对细节产生的信息增强，对噪声抑制，导致对比度过亮、视觉效果差，文献[19]算法对图像进行去噪，放大了图像的噪声，而所提算法对含噪图像增强后，有效地去除了图像的噪声，且对比度自然，更好地保留了图像的细节信息。

加入不同方差的乘性噪声，不同算法的峰值信噪比对比如表3所示。

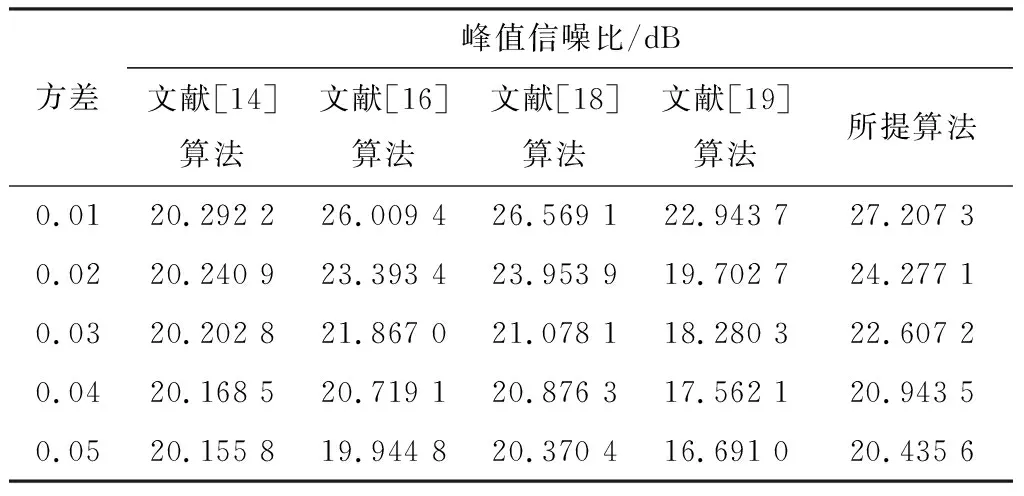
表3 加入乘性噪声后不同算法的峰值信噪比对比

由表3可知，对手指静脉图像加入方差相同的乘性噪声时，所提算法的峰值信噪比均高于其他算法，去噪效果较好。

综上，当加入加性高斯白噪声和泊松噪声时，所提算法的去噪效果明显优于其他算法。当加入椒盐噪声和乘性噪声时，随着噪声密度和方差的增大，所提算法的峰值信噪比明显下降，但还是优于其他频域上的图像增强算法。因此，所提算法在频域去噪效果方面优于其他算法。

4 结语

基于频域提出的基于改进阈值函数的手指静脉图像增强算法，将手指静脉图像进行二维小波变换，对所得到的低频子带系数进行非线性增强，保留了图像的边缘信息。对3个高频子带系数进行脊波变换，能够更好地处理线奇异性，利用改进阈值函数处理经脊波变换后的脊波系数，在频域上能够有效地降低噪声。最后，通过小波重构得到了增强后的手指静脉图像。实验结果表明，该算法能够降低噪声，减少失真并保留了较高的信息量，图像增强效果较好。