扩散火焰烟黑的数值模拟与参数优化
2021-03-12谢欣容
谢欣容,刘 石
(华北电力大学能源动力与机械工程学院,北京 102206)
0 引言
现代社会的能源主要由化石燃料的燃烧产生。燃料燃烧产生的污染排放和能源危机日趋严重[1]。其中,烟黑颗粒是化石燃料燃烧产生的主要污染成分之一,其排放不仅会降低燃烧效率,还会对人体和环境造成不利的影响:吸附在烟黑颗粒表面的多环芳烃(polycyclic aromatic hydrocarbons,PAH),会对人体健康造成危害[2];烟黑的连续辐射导致火灾中的火势不断生长和蔓延,阻碍了火灾救险和逃生;大气中的烟黑颗粒还会降低其能见度,给出行带来不便,并且增加了交通事故的风险。此外,烟黑也会对环境产生光化烟雾、消光效应及温室效应等不良现象[3]。因此,为了在实际应用中有效地研究烟黑形成和控制烟黑颗粒的排放,精确、可靠的预报火焰烟黑形成模拟技术就显得尤为重要。
经过几十年的发展,目前主要有三种烟黑模型用于燃烧系统计算[4]。详细的化学反应模型在数值上需求解速率方程,然而火焰燃烧反应过程十分复杂,使得详细的模拟计算在速度和存储量上都受到了很大的限制[5];纯经验模型通过调整模型参数以更好地匹配实验测量数据,会降低模型在其他试验条件下的通用性;半经验模型把烟黑形成的物理化学信息应用到数值计算中,促进了利用化学反应描述烟黑形成和控制机理研究的发展。本文描述的半经验双方程烟黑模型[6]基于实际相关性中的试验数据的输入,解决烟黑形成的速率方程,将物理现象与化学现象相结合。
本文以二维空间轴对称层流乙烯-空气扩散火焰为研究对象,采用正交分析法,选取对烟黑形成有影响的 5个重要因素进行优化数值模拟,并通过正交试验设计多种试验方案,进行相应的模拟计算。利用极差分析和方差分析阐明自变量因素对整体计算结果的影响程度和优化水平,从而得到与试验数据最接近的模拟模型。
1 正交试验设计
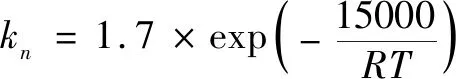
试验因素及其水平如表1所示。
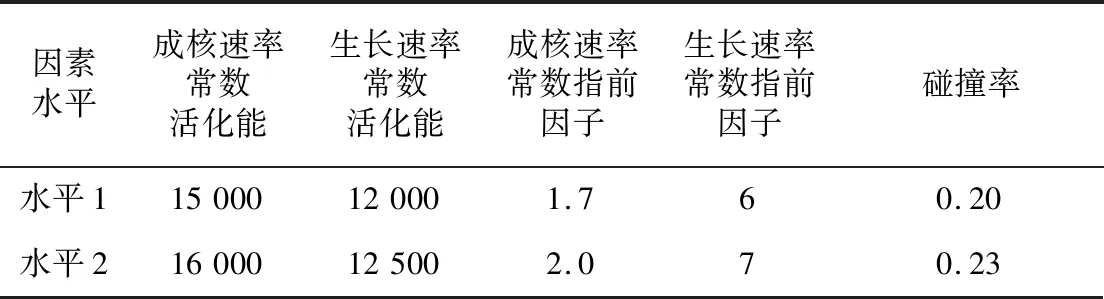
表1 试验因素及其水平表 Tab.1 Test factors and their levels
2 计算方法
本研究中的火焰结构是一个轴对称层流同向流乙烯-空气扩散火焰,燃料(乙烯)从内径为10.74 mm 的钢管中流出,体积流量为194 mL/min。氧化剂(空气)从燃料管和内径为88.62 mm的同心管中的空间区域流出,体积流量为284 L/min。燃料和空气在室温(300 K)下进行反应。
乙烯-空气火焰的试验数据来自文献[10]的高光谱试验结果。本文应用试验测量数据与模拟结果进行比较,以两者的温度均方根(root mean square,RMS)误差和烟黑颗粒浓度均方根误差的平均值作为评判标准,判断各模拟试验方案与试验结果的匹配度。
2.1 火焰配置和计算域
在大气压和室温(300 K)下的计算范围包括15.35 cm(z)× 6 cm(r)的二维矩形区域。将其分成333(z)×88(r)个控制体积。在z和r方向上使用非均匀网格。在r方向上的0~1.2 cm 区域间,网格采用精度更高的划分规则。网格布局在大梯度区域中提供了更高的分辨率,以减少不必要的计算时间。计算网格和边界条件如图1所示。

图1 计算网格和边界条件 Fig.1 Computational grid and boundary conditions
2.2 气相控制方程
乙烯-空气火焰燃烧涉及流体流动和化学反应等过程,在进行数值模拟时流体动力学的基本控制方程必不可少。参考文献[11]给出了轴对称圆柱坐标(r,z)中质量、动量、能量和化学组分的完全耦合控制方程。引力项包含在动量方程中,校正速度用于确保质量分数的总和为1。
2.3 数值计算
控制方程的离散应用控制容积法,压力与速度的耦合应用压力耦合方程组的半隐式方法(semi-implicit method for pressure linked equation,SIMPLE)数值算法。守恒方程中的扩散项应用中心差分的数值解离散,对流项应用逆风差分的数值解离散。为了提高数值计算的收敛速度,烟黑质量分数、烟黑数量密度、气体组分的离散方程均采用全耦合式方法进行计算。动量、能量和压力修正项的离散方程采用传热学中广泛应用的三对角矩阵算法(tridiagonal matrix algorithm,TDMA)求解。H2O、CO2和 CO 的非灰辐射特性采用离散坐标法(discrete-ordinates method,DOM)求解。
计算涉及的气相反应基于GRI3.0 机理获得。其中,不包括与NOx生成相关的反应和组分。更改后的反应机理包含36 个组分和219 种反应,所用的热力学特性与传输数据是依据GRI 3.0 数据库与CHEMKIN 代码得到。
3 试验结果及分析
正交试验方案及其模拟计算结果如表2所示。
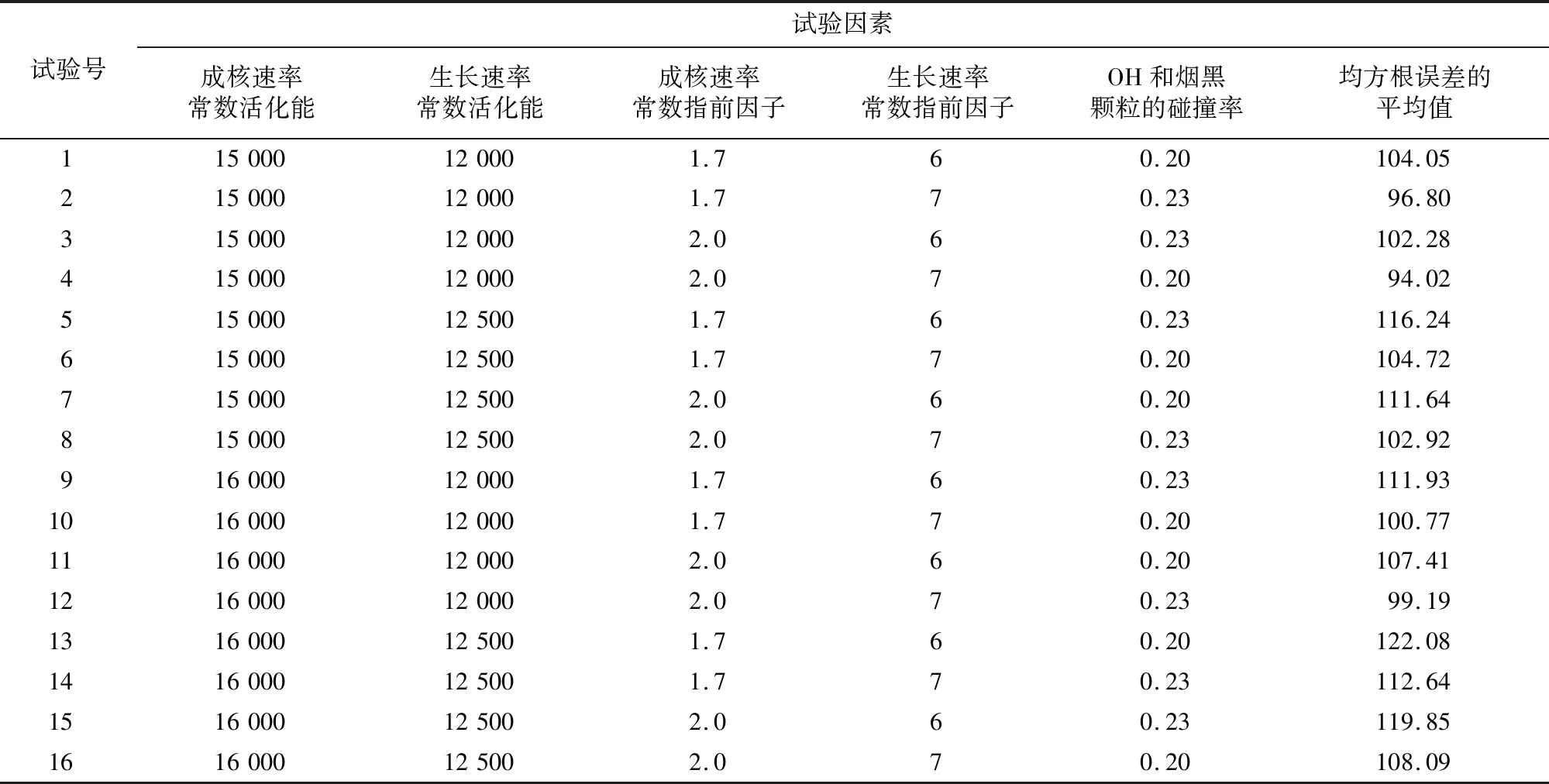
表2 正交试验方案及其模拟计算结果 Tab.2 Orthogonal test scheme and its simulation calculation results
3.1 试验因素对烟黑模型的影响
试验结果表明,在其他因素不变的情况下,当成核速率常数活化能和生长速率常数活化能同时增大时,均方根误差的平均值明显增大;而在成核速率常数活化能增大、生长速率常数活化能减小时,其均方根误差的平均值显示下降的趋势。例如1号、13号试验和5号、9号试验进行比较。成核和生长速率常数活化能对均方根误差平均值的影响如图2所示。

图2 成核和生长速率常数活化能对均方根误差平均值的影响 Fig.2 Influences of nucleation and activation energy of growth rate constant on mean RMS error mean
由图2可以判断出,在有效区域内,生长速率常数活化能减小可以使均方根误差平均值减小,即可以提高模型与试验结果的匹配度。成核速率常数活化能和生长速率常数指前因子对均方根误差平均值的影响如图3所示。

图3 成核速率常数活化能和生长速率常数指前因子对均方根误差平均值的影响 Fig.3 Nucleation rate constant activation energy and growth rate constant refer to the influence of the pre-exponential factors on the mean RMS error
在其他因素不变的情况下,成核速率常数活化能和生长速率常数指前因子同时增大时,均方根误差的平均值减小;而当成核速率常数活化能增大、生长速率常数指前因子减小时,均方根误差的平均值呈增大趋势。由此说明,生长速率常数指前因子减小使均方根误差的平均值增大,即增大生长速率常数指前因子可以提高数值模拟对试验的匹配度。例如3号、12号试验和4号、11号试验进行比较。
3.2 极差分析
运用极差分析法,分别对 16 组试验指标进行分析。各因素不同水平的均方根误差的平均值和极差如表3所示。

表3 各因素不同水平的均方根误差的平均值和极差 Tab.3 Mean and range of RMS errors at different levels of each factor
由表3可知,各因子对试验和模拟的均方根误差平均值的主次影响关系,以及较优水平组合。
4号试验的烟黑容积份额分布如图4所示。

图4 4号试验的烟黑容积份额分布图 Fig.4 Distribution of soot volume fraction in test No.4
①因素的主次关系。根据极差R的变化,可以判断各因素对计算结果的影响程度。极差越大,对应的因素影响越重要。第2列和第4列的极差分别是40.86和38.18,是所有极差中最大的两个,表明生长速率常数活化能和生长速率常数指前因子对试验结果的影响较大,是主要的影响因素;而成核速率常数活化能和成核速率常数指前因子对均方根误差平均值的影响较小,是次要因素;OH与烟黑颗粒的碰撞率对均方根误差平均值的影响程度最小。
②较优水平组合。根据k1、k2的大小,确定5个因素取哪个水平好。由于对指标的要求是试验数据和模拟结果的均方根误差平均值最小为最优模型,所以k1、k2值越小越好。因此,取最小的k值所对应的因素水平依次是15 000、12 000、2、7、0.2,即4号试验条件的数值模拟结果与高光谱试验测量结果最接近。
3.3 方差分析
表4是回归分析统计表。其中,相关系数为0.893,用于衡量各个因素与计算结果之间的相关程度,表明他们之间的关系为高度正相关。复测定系数为0.797,用于表征各因素解释计算结果变差的程度,以测定计算结果的拟合效果。本数据表明,各因素可解释计算结果变差的79.73%。调整后的复测定系数为0.696,说明各因素能解释说明计算结果的69.60%,即计算结果的30.40% 由其他因素来决定。标准误差为0.012,用于衡量各因素与计算结果拟合程度。数值越小,表明拟合效果越好。

表4 回归分析统计表 Tab.4 Regression analysis statistics
表5为方差分析表,主要通过F检验来判断回归模型的回归效果。F显著性统计量的P值为0.00 304,小于显著性水平0.05;因此,该回归方程回归效果显著。

表5 方差分析 Tab.5 Variance analysis
表6为回归参数表。其中,Esf和ksf的统计量t的P值远小于显著性水平0.05,说明该两项的自变量与因变量相关性显著。

表6 回归参数表 Tab.6 Regression parameter table
4 结论
本文利用 Fortran语言对层流乙烯-空气火焰进行数值模拟,得到了火焰温度和烟黑体积分数,进而计算了其对应试验和模拟之间的均方根误差的平均值;通过正交试验设计,研究了各个因素对烟黑体积分数的影响。研究结果表明,针对乙烯-空气火焰中烟黑影响因素及水平较多的情况,使用正交试验设计数值模拟,用少量具有代表性的试验研究了各个因素对烟黑造成的影响。
通过对试验结果的极差分析可知:生长速率常数活化能和生长速率常数指前因子对均方根误差平均值有显著的影响,而成核速率常数活化能、成核速率常数指前因子、OH和烟黑颗粒的碰撞率对均方根误差平均值影响相对不显著。因此,在优化设计中,可适当减小生长速率常数活化能和增大生长速率常数指前因子。
