杯式风速传感器计量的线性研究
2021-03-12张艺萌朱明宇
沙 莉 ,罗 昶,支 询 ,李 施 ,张艺萌 ,朱明宇
(1.辽宁省气象装备保障中心,辽宁 沈阳 110166;2.浙江省大气探测技术保障中心,浙江 杭州 311106)
0 引言
风是空气流动引起的一种自然现象。空气运动可分解成垂直和水平两个方向的分量。垂直分量称为空气的对流运动。风一般指的是空气的水平运动。
杯式风速传感器由等角度间隔的3个椎形杯体及支架组成,风杯在水平风力的推动下产生旋转,其转动频率与风速成线性关系。风速传感器的线性关系可直接反映传感器空气动力学结构特征,与风标形状尺寸、旋转半径等结构尺寸比例有关。已有研究证明,风速传感器的非线性误差与两种因素相关:①动力学特性引起的过高效应[1-4];②转动轴与地面不垂直程度。
1 方法与资料获取
1.1 误差来源分析
杯式风速传感器结构如图1所示。风杯中心点与支架的距离Rrc和杯体半径Rc的比例决定了传感器的动力气象学特性。

图1 风速传感器结构图 Fig.1 Structure of wind speed sensor
理论上,杯式风速传感器的输出值V(m/s)与输出频率f(Hz)可通过线性方程实现。
V=Af+B
(1)
式中:A为理想线性方程斜率;B为截距。
在实际测量时,输出频率f通过测量内部电路转子转速获得。每旋转1圈,霍尔开关电路感应出18个脉冲信号[5]。由于风杯部件的结构特征带来的迟滞效应和机械摩擦[6],造成低风速输出f与传感器实际的旋转频率fR不完全相同,故输出值V与实际测量的输出频率fR的线性方程为:
式中:AR为测量线性方程斜率;B为截距。
AR与A成倍数关系,可假设为A=m×AR。其中,AR和B的计算公式为:
(3)
由式(1)可见,对风速传感器线性关系的分析可直接推导出由传感器结构特征带来的测量误差影响量。杯式风速传感器测量误差分析方程为:
U=UI×uerror×werror×DDPerror
(4)
式中:U为测量时标准值;UI为传感器输出的测量值;werror、uerror为测量时湍流特征对风速传感器的影响因子;DDPerror为传感器感应风向偏离水平而引起的影响量。
uerror(过高效应)来源于旋转式风速传感器本身的非线性,即风速增大时比风速减小时响应更快,造成平均风速测量值偏大。werror的来源是转动轴与地面不垂直形成的误差。关于werror和uerror的数值大小,多位学者进行了定量的研究。其中,Kaganov和Yaglom[7-8]认为两项误差之和约为总误差的(8~10)%。利用归一化标准差和稳定度参与变化和通量-廓线关系,对DDPerror进行修正,而werror、uerror则与传感器本身的误差相关。
1.2 试验方法
目前,我国风速计量试验多在风洞装置中展开。风洞装置分风场控制装置、风速测量系统和数据处理单元3部分组成。风洞装置组成[9]如图2所示。

图2 风洞装置组成图 Fig.2 Wind tunnel installation composition
风场控制装置由供电系统、变频系统和风机控制系统组成。通过变频系统改变风机转速,在风洞试验段形成水平、稳定、均匀的风场环境,风场内流速稳定性和均匀性可达到0.5%[10]。风速测量系统由皮托静压管和数字微压计组成的计量标准器、杯式风速传感器、数据采集系统组成。计量标准器测量风流动过程中的动压,依据流体动力学的伯努力方程,计算得到气流的标准速度V。杯式风速传感器的风杯在稳定风力的作用下绕垂直轴旋转。风杯的转速与风速呈线性关系。通过数据采集系统可分别获得计量标准的动压P(Pa)和杯式风速传感器的转速频率f(Hz)在同一风场环境下的测量值,经过数据处理换算成同一量纲V(m/s),并采用比较法开展误差分析。
1.3 数据来源
试验数据有2种。推导数据是在消除阻塞的理想环境中,对同一传感器依据检定规程的方法进行8次全量程重复性测量,对试验数据开展线性度分析。验证数据是针对同一型号的杯式风速传感器,在广西、山东、辽宁、广东等省级气象计量试验室的检定记录中采集相关数据进行线性度分析,并与推算结论进行方法验证及比对,确认在不同环境下测量方法的实用性。
2 数据比对分析
一般用线性度指标衡量传感器的线性优劣程度。采用本文1.2节所述的试验方法,对不同测量点的传感器输出值进行独立线性度分析,计算传感器实际平均输出特性曲线对最佳直线的最大偏差,并采用最小二乘法[11-12]对传感器线性输出值进行最大似然估计。
(5)
式中:S2为测量值和估计值之间的差异方差;n为测量次数;V标为标准风速值;V测为传感器输出值。
在获得测量值和参考值的最优估计后,将标准值代入估计线性方程x,得到估计值与传感器实际输出值的差值,即传感器在该测量点的非线性误差。
2.1 单支传感器重复测量线性比对分析
对单支传感器全量程重复测量8次,得到的单一传感器重复性测量非线性误差如表1所示。

表1 单一传感器重复测量非线性误差 Tab.1 Single sensor repeated measurement nonlinear error list m/s
传感器全量程校准非线性误差如图3所示。

图3 传感器全量程校准非线性误差示意图 Fig.3 Schematic cliagram of calibration of nonlinear error at full range of sensor
8组数据测试结果表明,非线性误差偏大的部分集中在两端测量点,即高速(50 m/s以上)、低速(5 m/s以下)。低速检测时,正偏差较大,说明传感器输出值比估计值低。随着风速的测量值增高正偏差逐渐减少,传感器的线性输出值接近或超过估计值。由此可以看出,低速时误差的主要是由uerror过高效应导致。高速检测过程中,风速加大导致转动轴与地面不垂直的影响量增大,传感器输出值又低于估计值。由此可知,误差来源以werror为主,故最小二乘似然估计法可用于传感器的线性特征分析。由图3可直观地表明上述分析结论:线性技术指标的最大允许误差限为±0.5 m/s,通过试验数据计算得到的非线性误差均在合格范围内;但两端测量点的非线性偏差明显增大,中间测量点更加接近估计值。
2.2 同一型号传感器测量结果对比
在广东、山东、广西、辽宁四省的检定记录中,抽取8支同一型号、不同编号的杯式传感器检定记录,对测试结果进行数据分析。记录中无高风速测量点的测量,所以只对2~30 m/s的测量结果应用本文2.1节所述的线性分析方法。同型号传感器在不同试验环境测量的非线性误差如表2所示,校准非线性误差如图4所示。由表2、图4可以看出,在低速(5 m/s以下)测试点的非线性误差值并没明显增大。经分析,确定在风洞试验段的直径与传感器体积投射比例偏小时会带来偏差。此外,还存在着由标准装置检测的不确定度影响因子(如装置的阻塞效应及皮托管静压测量[12]带来的系统误差等)综合形成的测量误差,直接用非线性误差的数值表现uerror已无明显的特征。

表2 同型号传感器在不同试验环境测量的非线性误差列表 Tab.2 Nonlinear error list of measurement in different test environments for the same type of sensor m/s

图4 校准非线性误差示意图 Fig.4 Calibration nonlinear error diagram
3 传感器测量线性分析
为了更好地分析传感器的线性,可采用独立线性度的分析方法,计算公式为:
(6)
式中:L为独立线性度;Δymax为各测量点非线性误差值的最大偏差;(yinmax-yinmin)为测量范围。
对同型号传感器不同试验环境的测量结果,依据式(4)分别计算线性度。各省试验数据线性度分析结果比对如表3所示。
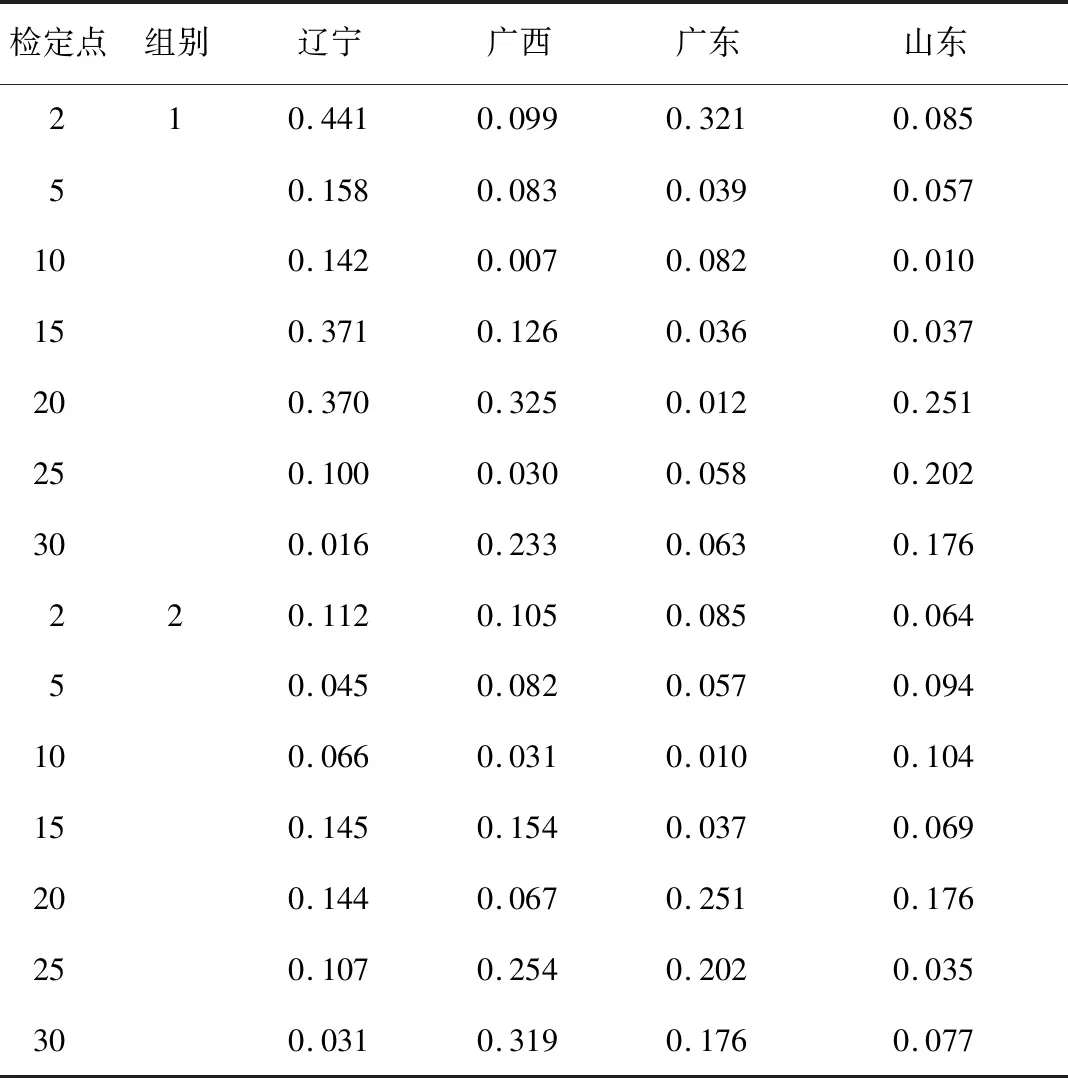
表3 各省试验数据线性度分析结果比对 Tab.3 Comparison of linearity analysis results of several provinces %
分析结果表明,尽管测量结果均符合最大允许误差的计量技术指标要求,但个体的线性值还存在很大差异,用满量程输出的百分数表示线性度的方法,可得到各测量点的独立线性度。取各测量点独立线性度最大值作为该传感器线性度。例如:第一组测量结果的线性度分别为0.4%、0.3%、0.3%和0.3%;第二组测量结果的线性度分别为0.1%、0.3%、0.3%和0.2%。杯式风速传感器的线性性能指标要求为±0.5 m/s,测量范围为0~60 m/s,则线性度误差限为±0.8%,可通过估计值线性方程推算的传感器线性度判定为合格。
各省检定数据线性度分析结果如图5所示。
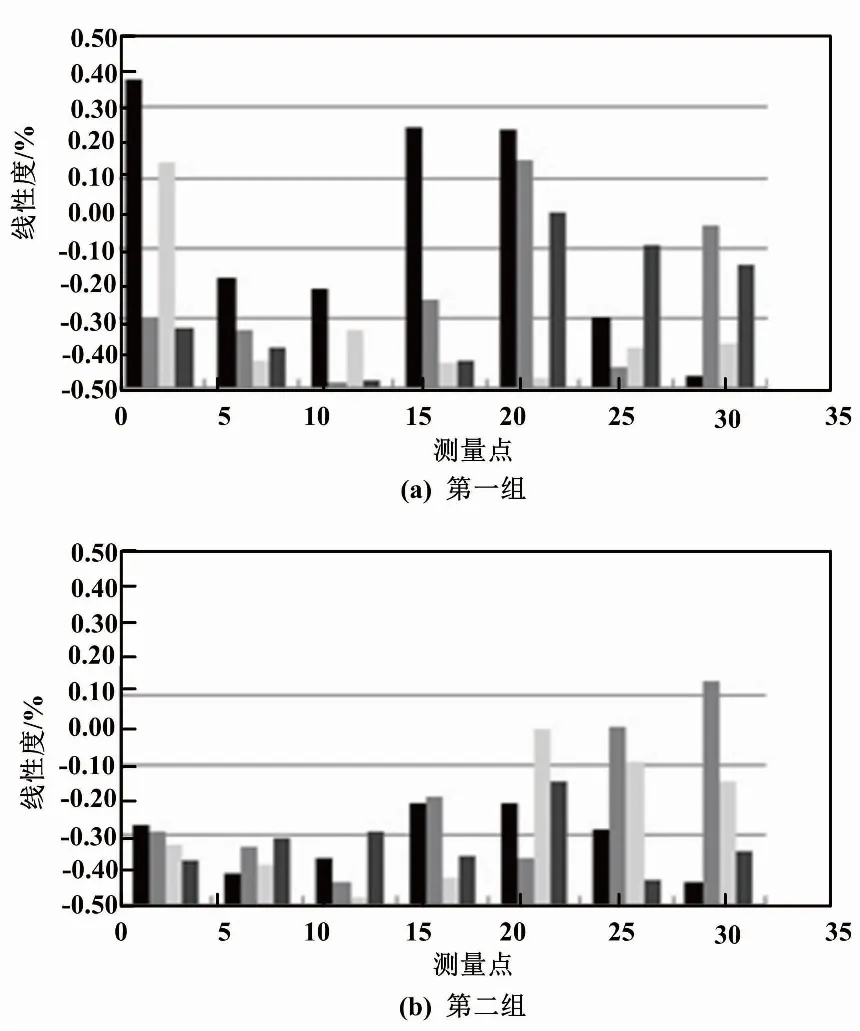
图5 各省检定数据线性度分析结果 Fig.5 Linearity analysis reswlts of test data of several provinces
4 结论
本文采用最小二乘法对杯式风速传感器的线性输出值进行最大似然估计,得到最佳直线的线性方程。通过对非线性误差的分析,引入线性度得到评价传感器的线性特征的方法。无论对传感器线性结果判别,还是传感器数据修正方面都是非常必要的,可为传感器的数据修正、结果评定等方面提供参考。
①应用非线性误差值,可有效分析传感器线性特征。最佳直线的拟合建议以标准值为输入量x,传感器读数为输出量y。得到的线性度可开展对传感器的线性计量特性评价。
②在进行传感器线性计量特性评价时(尤其在低风速测量)时,还要考虑由阻塞及皮托管标准装置带来的影响因素。因此,应尽量选择试验段口径偏大和提高低速计量标准等级等方法,以减少由计量标准装置引入的系统误差,从而提高uerror在误差分析中的权重比例、提升线性度评价的准确性。
