基于订单生产的供应链价格与承诺交货时间决策和协调

谢祥添

（广东金融学院 科技金融重点实验室，广东 广州 510521）

0 引言

许多企业成功的关键在于具有时间竞争优势[1]。So和Song[2]提出企业以时间作为武器吸引顾客有三种策略：①快速服务；②提前预约；③承诺交货时间。其中，订单生产一般采用第三种策略。在需求受价格和承诺交货时间影响的市场中，顾客倾向于购买价格低和承诺交货时间短的产品[3]。然而，较低的价格导致收入减少，较短的交货时间导致成本上升[4]。那么，企业如何决策才能使得利润最大化成为学者关注的问题。

延期是影响订单生产供应链竞争力因素之一。延期不仅导致罚款（Slotnick 和Sobel[5]提及飞机零部件供应商延期交货赔偿几百万美元的事例），还会影响企业声誉，失去未来顾客。因为订单生产过程随机性较大（相对标准化生产），延期频发，同时交货往往可提前，不可推迟。为此，企业可承诺一个可靠性（在承诺交货时间内交货的概率，部分文献称之为交货时间服务水平[6]，简称服务水平）较高的交货时间来减少延期的发生。

本研究内容主要涉及供应链价格与承诺交货时间决策和协调研究，以下就这两方面的文献进行简要的论述。

关于供应链价格与承诺交货时间决策研究，较早的是Pekg，等[7]，他们研究了生产部门对交货时间和销售部门对价格分散决策问题，得出了相对集中决策，分散决策策略为采用较长的交货时间和较低的价格，这与本研究的两个企业分散决策策略相反。Pekg，等[8]将文献[7]的问题拓展到两个企业竞争的情况，研究表明：在激烈的价格竞争中，企业应采用集中决策，在激烈的交货时间竞争中，企业应采用以销售部门为领导者的分散决策。以上是一个企业两部门分散决策，更多学者研究了两个企业分散决策。两个企业分散决策会产生双重边际化效应，所以研究的焦点为如何降低双重边际化效应。如，Liu，等[9]构建了以生产商对交货时间决策，以销售商对价格决策的分散决策模型，并以集中决策为基准分析分散决策效率不高的原因，提出柔性生产能有效地改善由于双重边际化导致分散决策低效问题。Zhu[10]从另一个角度研究了文献[9]问题，构建了以生产商对产能决策、以销售商对价格和交货时间决策的分散决策模型，证明了优化产能能有效降低双重边际化效应。赵晓敏和胡淑慧[11]针对B2C供应链高退货现象，研究了B2C供应链决策和协调机制，提出只有当产品质量达到一定条件，供应链才能实现协调，适当延长交货期可以使供应链协调相对容易实现，并且对于增加协调利润也有一定的正向作用。从以上文献可知，提高运营能力（柔性生产、优化产能等）可以降低双重边际化效应。本研究针对订单生产延期现象，构建以承诺交货时间满足一定的服务水平为条件的供应链价格与交货时间决策模型，研究发现提高服务水平也可以降低双重边际化效应。

供应链协调常用的方式有数量折扣、回购和收益分享。Zhang，等[12]通过收益分享与回购等方式的对比，证明收益分享在供应链协调中具有一定的优势。此外，Panda[13]指出收益分享能有效协调需求受内生变量影响的供应链各个成员。本研究为需求受价格和承诺交货时间内生变量影响，所以采用了收益分享方式构建供应链协调模型。

综上所述，本研究的贡献为：针对订单生产需求受价格和承诺交货时间影响以及延期现象，考虑服务水平，建立供应链价格与交货时间决策模型，得到了模型的最优价格和最优承诺交货时间，据此分析它们与相关参数的关系，得到了一些管理启示。此外，采用收益分享方式构建供应链协调模型，以集中决策为基准设计一个协调方案，得出销售商收益分享比例处于某一范围内才能实现供应链的协调。

1 模型假设和符号定义

1.1 模型假设

假设1：生产商为领导者，销售商为追随者，销售商与生产商之间的博弈为Stackelberg博弈；

假设2：生产商与销售商之间的需求信息是对称的，即生产商和销售商的需求相同；

假设3：订单生产过程为M/M/1 排队模型，即需求时间间隔和生产时间服从负指数分布，且采用先来先生产。

1.2 符号定义

p：销售价；

w：批发价；

cs：销售单位成本；

cm：生产单位成本；

u：产能；

cu：产能单位成本；

l：承诺交货时间；

s：服务水平，s∈(0,1)；

λ：需求率（单位时间需求量），考虑顾客倾向于购买承诺交货时间短、价格低以及服务水平高的产品，构建需求率函数为：

其中，λ01为潜在需求，α 为需求关于价格敏感系数（简称价格敏感系数），α>0，β 为需求关于承诺交货时间敏感系数（简称承诺交货时间敏感系数），β>0，γ 为需求关于服务水平敏感系数，γ>0。为了表达简便，设λ0=λ01+γs。

L：实际交货时间；

P{L≤l}：实际交货时间小于等于承诺交货时间的概率。文献[14-15]指出在M/M/1 排队模型下实际交货时间小于等于承诺交货时间的尾概率分布近似服从负指数分布，即：1-P{L≤l}=e-l/γ，其中γ为均值。根据假设3，需求时间间隔服从1/λ的负指数分布，生产时间服从1/u 负指数分布，这时有γ=1/(u-λ)。所以，实际交货时间小于等于承诺交货时间的尾概率分布为：1-P{L≤l}=e-(u-λ)l。若考虑承诺交货时间满足一定的服务水平（实际交货时间小于等于承诺交货时间的概率大于等于某一服务水平），则有：

本研究采用上标来区分不同模型。设上标c，d和t分别表示集中决策模型、分散决策模型和协调模型，同时，上标c，d和t也分别表示对应每一个模型的变量取最优值。下标m 和s 分别表示生产商和销售商。

2 分散决策模型与集中决策模型

2.1 分散决策模型

根据假设1，生产商作为领导者具有主动权，它会依据销售商的反应（销售价决策）对批发价和承诺交货时间作出决策，以获得自身利润最大化；销售商作为追随者则根据观察到的批发价和承诺交货时间对销售价作出决策，以获得自身利润最大化。因此本研究从销售商优化开始，通过逆向归纳法得出博弈均衡。

建立以销售价为决策变量、以销售商单位时间最大利润为目标函数模型：

求解式（3）可得最优销售价为：

考虑承诺交货时间满足一定的服务水平，建立以承诺交货时间和批发价为决策变量，以生产商单位时间最大利润为目标函数模型：

命题1：在分散决策模型中，存在最优批发价和最优承诺交货时间，它们分别为：

其中λd为f(λ)=0的实根，f(λ)为：

其中，k=-ln(1-s)。

证明：把式（4）代入式（1）可得批发价为w=(λ0-αcs-βl-2λ)/α，所以式（5）可转化为：

解式（9）的条件可得l≥-ln(1-s)/(u-λ)，设k=-ln(1-s)，则有l≥k/(u-λ)。因为式（9）关于l 为单调减函数，所以l=k/(u-λ)时，式（9）关于l取最大值。因此，式（9）可转化为只含λ为变量的优化问题：

命题1结论：分散决策模型存在最优承诺交货时间和最优批发价。其中ld=k/(u-λd)表明最优承诺交货时间存在于式（5）条件边界上，即最优承诺交货时间绑定在服务水平上。

把ld和wd=(λ0-αcs-βld-2λd)/α 代入式（4）可得最优销售价为：

2.2 集中决策模型

考虑承诺交货时间满足一定的服务水平，建立以销售价和承诺交货时间为决策变量，以单位时间最大利润为目标函数模型：

命题2：在集中决策模型中，存在最优销售价和最优承诺交货时间，它们分别为：

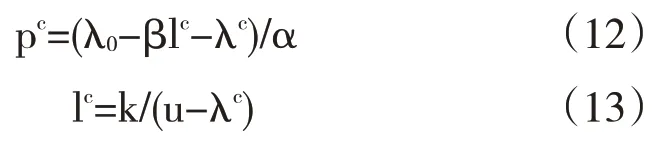
λc为h(λ)=0的实根，h(λ)为：

证明：根据式（1）得：p=(λ0-λ-βl)/α，把它代入式（11）有：

解式（15）的条件可得l≥k/(u-λ)，又因为式（15）关于l为单调递减函数，所以l=k/(u-λ)时，式（15）关于l取最大值。因此，式（15）可转化：

因为d2Πc(λ)/dλ2=[-2βku-2(u-λ)3]/[α(u-λ)3]<0，所以存在最优利润,其对应最优λc满足Πc(λ)一阶偏导数为 0:dΠc(λ)/dλ={[λ0-2λ-(cm+cs)α](u-λ)2-βku}/[α(uλ)2]=0，设h(λ)=[λ0-2λ-(cm+cs)α](u-λ)2-βku，所以λc需满足h(λ)=0。与命题1证明f(0)>0和f(u)<0同理，可得h(0)>0，h(u)<0，所以h(λ)在(0,u)必存在一个实根，把λc代入l=k/(u-λ)可得最优交货时间为:lc=k/(u-λc),把λc和 lc代入 p=(λ0-λ-βl)/α 可得最优销售价为:pc=(λ0-βlc-λc)/α，至此证毕。

命题2结论：集中决策最优决策变量表达式与分散决策相似，不同在于最优需求率满足方程中-λ(uλ)2的系数：集中决策为2，分散决策为4。

2.3 分散决策与集中决策比较

分散决策总利润为销售商利润加生产商利润，把最优解代入式（3）和式（5）求和化简可得分散决策最优总利润为：

根据命题2可得集中决策最优利润为：

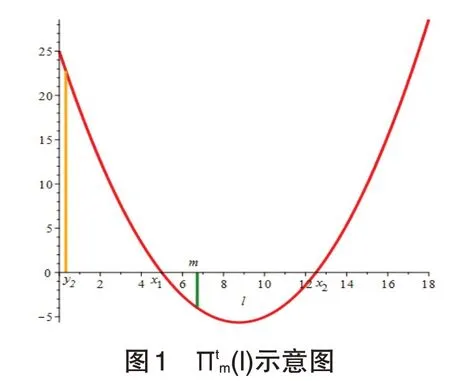
命题3：Πc>Πd，λc>λd，lc>ld，pc

证明：因为式（16）与式（17）关于需求率具体相同的表达式，它们关于需求率二阶导数小于0，所以式（16）与式（17）存在最大值，又因为λc满足式（17）关于需求率一阶导数为0，λd不满足式（16）关于需求率一阶导数为0，所以Πc>Πd。由式（8）和式（14）可得[λ0-(cm+cp)α-2λc](u-λc)2=[λ0-(cm+cp)α-4λd](u-λd)2，所以{2λc-[λ0-(cm+cp)α]}/{4λd-[λ0-(cm+cp)α]}=(u-λd)2/(uλc)2，因此λc>λd。因为lc=k/(u-λc)，ld=k/(u-λd)和λc>λd，所以 lc>ld。因为 pd=(λ0-βld-λd)/α，pc=(λ0-βlc-λc)/α，λc>λd和lc>ld，所以pc

命题3 结论：相对集中决策，分散决策采用较高的价格和较短的承诺交货时间，其最优利润和最优需求都较少。

3 协调模型

设θ1为销售商的收益分享比例，θ1>0，θ2为生产商的收益分享比例，θ2≥0，且θ1+θ2≤1，特别地，当θ2=0和θ1=1 为分散决策模型，那么销售商单位时间最大利润为：

生产商单位时间最大利润为：

命题4：在协调模型中，存在最优销售价，最优需求率和最优承诺交货时间，它们分别为：

其中w的范围满足不等式（23）：

证明：把式（1）代入式（18）后可求解出最优销售价为：

把式（24）代入式（1）可得最优需求为：

把式（24）和（25）代入式（19）可得只含承诺交货时间为变量的最大利润：

根据式（26）的条件，设g(l)={u-[(λ0-βl)/2-(cs+w)α/(2θ1)]}l-k。g(l)=0 有两个根，设它们分别是y1和y2，且y1≤y2。又因为g(0)=-k<0，所以l≥y2，其中y2为：

根据式（25）需求大于等于0可得l≤λ0/β-(cs+w)α/(θ1β)，设m=λ0/β-(cs+w)α/(θ1β)，因为Πtm(m) =-cuu<0,设Πtm(l)的两个根为分别是x1和 x2，且 x1≤x2。因为 d2Πtm(l)/dl2=θ2β2/(2α)>0，开口向上，所以只有 y2

根据y2

至此证毕。

根据命题4 可知，要实现供应链协调，还需要确定θ1，θ2和w，这些参数可通过生产商与销售商之间的协商予以确定。本研究以集中决策为基准设计一个协调方案，即推论1。

推论1：当θ2=0，θ1=1和w=wt时，协调模型最优决策与集中模型最优决策相同，即pt=pc，lt=lc和Πtm+Πts=Πc。其中wt表达式为：

证明:设λ=λc和l=lc=k/(u-λc)，由式（1）和式（25）可得:λc=(λ0-βk/(u-λc)/2-α(cm+w)/(2θ1)，解 w 得：w=θ1[λ0-βk/(u-λc)-αcs-2λc]/α，因为θ1=1，所以得式（27）。又因为把wt代入式（22）可得lt=k/(u-λc)=lc，把w=wt和l=lt代入式（21）得λt=λc，把w=wt和l=lt代入式（20）得pt=[(λ0-λc)(u-λc)-βk]/[α(u-λc)]=[(λ0-λc)-βk/(u-λc)]/α=[(λ0-λc)-βlc]/α=pc，把 p=pc，λ=λc，l=lc以及θ2=0 和θ1=1代入式（18）和式（19）求和可得Πt m+Πt s=Πc。最后把θ2=0，θ1=1 代入式（23）可得(w-cm)α>0，表明wt范围满足不等式式（23）。至此证毕。

4 模型分析

（1）最优决策变量与相关参数分析。对最优承诺交货时间与相关参数分析，可得它们与相关参数的关系，见表1。

表1 最优承诺交货时间与相关参数的关系

关于最优价格与s，α，β的关系，本研究通过数值分析给出。设cs=0.8，cm=1.5，cu=0.2，u=10，λ01=21，γ=10，s=0.9，β=4，α=2 为基础数据，作pc，pd与s，α，β 的关系，如图2至图4所示。

图2 pc，pd与s的关系

图3 pc，pd与α的关系

图4 pc，pd与β的关系

（2）最优利润与相关参数分析。利用基础数据作集中决策，分散决策和协调模型的最优利润与相关参数的关系，如图5至图7所示。

图5 Πc，Πd与s的关系

图6 Πc，Πd与β或α的关系(α=2或β=2)

从图5可知，集中决策与分散决策的最优利润随着服务水平的提高相差越来越小，这说明提高服务水平可以降低双重边际化效应。

从图6可知，集中决策与分散决策的最优利润随着价格敏感系数和承诺交货时间敏感系数的增加而减少，价格敏感系数比承诺交货时间敏感系数更显著。这说明价格的变化对利润的影响大于承诺交货时间。

从图7可知，①协调模型销售商最优利润和最优总利润随着销售商收益分享比例的增加而增加，协调模型生产商最优利润随着销售商收益分享比例的增加先增加后减少。当销售商收益分享比例等于1时，协调模型销售商最优利润和生产商最优利润相交，这时协调模型最优总利润最大，它等于集中决策最优利润（见推论1）；②当0<θ1<0.247 时，协调模型最优总利润小于分散决策最优总利润，这时协调模型是无效的；③当0.247<θ1<0.611和0.808<θ1<1时，协调模型虽然有效（协调模型最优总利润大于分散决策最优总利润），但不稳定（当0.247<θ1<0.611 时，协调模型销售商最优利润小于分散决策销售商最优利润，当0.808<θ1<1 时，协调模型生产商最优利润小于分散决策生产商最优利润）。④当0.611<θ1<0.808时，协调模型生产商最优利润大于分散决策生产商最优利润，协调模型销售商最优利润大于分散决策销售商最优利润，即协调模型实现了帕累托改善。所以，销售商收益分享比例处于某一范围内才能实现供应链的协调。

5 结语

在订单生产下，延期频发，本研究考虑服务水平，建立供应链价格与承诺交货时间决策和协调模型。研究表明：①最优承诺交货时间绑定在服务水平上，提高服务水平可以降低双重边际化效应，但是过高服务水平会导致利润下降；②相对集中决策模型，分散决策模型采用较高的价格和较短的承诺交货时间，其最优利润和最优需求较少；③销售商收益分享比例处于某一范围内才能实现供应链的协调。

本研究假设生产商与销售商的需求信息是对称的，实际上，需求信息多为不对称，同时也有以销售商为领导者，所以未来可研究需求信息非对称下销售商为领导者的供应链决策和协调。