含双承压水地层中地连墙槽壁稳定性有限元分析
2021-03-12周忠群张孟喜薛青松
周忠群,张孟喜,王 鑫,张 强,薛青松
(1.上海大学力学与工程科学学院,上海 200444;2.中铁二十局集团第一工程有限公司,江苏 苏州 215151)
随着城市地下空间不断开发,地下连续墙技术也得到广泛运用,地下连续墙成槽过程中槽壁稳定性控制一直是施工质量控制的一项重点工作,而地连墙槽壁稳定性分析一直是岩土工程中的一个难点问题,正确地分析槽壁稳定性,对于确保工程质量安全和工程成本控制具有十分重要的意义。影响槽壁稳定性的因素很多,而对于穿湖地层的地连墙成槽施工,地下水的渗流作用无疑是影响其稳定性的主要因素之一。
当前,国内外学者对渗流作用下的地连墙槽壁稳定性问题作了大量的研究工作。黄锋[1]考虑成槽开挖时的渗流作用,基于极限分析上限定理,构建运动速度机动场对地连墙局部和整体失稳模式进行了分析;刘杨等[2]针对富水软弱地层地连墙进行研究,考虑了承压水作用,基于极限平衡方法分析了槽壁局部失稳机制;Liu等[3]考虑了渗流作用,采用渗流解析模型方法对槽壁进行局部稳定性分析;李建高等[4]考虑了水的渗流作用对槽壁稳定性进行分析,采用解析方法和二维数值计算得出槽壁的安全系数;孟德平[5]考虑了地下水位的影响,采用有限元强度折减法对槽壁稳定性进行分析。以上学者虽然考虑了地下水的渗流作用,但均未对双承压含水层槽壁失稳模式进行研究,且缺乏对水的渗流场分析。
考虑渗流作用下地连墙槽壁稳定性分析是一个比较复杂的问题,目前,槽壁稳定性分析方法主要有极限平衡法、有限元法和有限差分法。其中,有限元强度折减法不需要假定破坏面的形状和位置,也能定量反映出地连墙槽壁的渐进失稳演化过程。因此,本文依托苏州春申湖路快速化改造工程为背景,采用ABAQUS软件基于强度折减法对穿湖地层双承压含水层地连墙成槽施工进行槽壁失稳破坏模式分析,有限元强度折减法通过不断调整折减系数对槽壁稳定性进行分析,从而确定滑裂面位置和滑动体形状,揭示双承压含水层槽壁失稳破坏模式及破坏过程,并结合现场声波实测进行对比分析。
1 槽壁破坏特征及强度折减分析
1.1 渗流作用下地连墙失稳破坏过程
目前,学者们普遍认为边坡失稳破坏具有渐进破坏特征[6-8],根据以往大量工程实际案例以及学者们的研究发现,地连墙槽壁失稳破坏和边坡失稳破坏存在类似特征,槽壁失稳往往表现为局部塌孔向整体滑动演化的渐进破坏过程,并非一次瞬间完成。由于地连墙槽壁土层本身存在局部软弱土层,且在高水位区进行成槽开挖,渗透系数较大的粉砂层对地下水的渗流力作用影响较为明显,往往容易最先出现局部应力集中现象,从而使这部分土体单元最先出现局部塑性破坏区。随着局部塑性破坏区不断扩大,局部塑性区的应力集中会出现转移和调整,新的应力集中带会形成,之后应力集中带会不断发展扩大,最终会在槽壁土体形成贯通的塑性破坏滑裂带。
边坡的滑裂带具有软化特性[9],地连墙槽壁也具有类似性质,在达到抗剪强度峰值会降到残余值,含承压水的双粉砂层槽壁渐进破坏过程见图1,塑性滑裂带起于含承压水的薄弱粉砂层底部,即点a处,在点a和b,土体剪应力超出峰值点并降到残余值,点c的剪应力刚达到峰值,而点d的剪应力远低于峰值抗剪强度。随着滑裂带的渐进扩展,双粉砂层之间的点d也将出现应力集中并达到峰值点,滑裂带由潜在滑裂面渐进扩展并形成最终贯通滑动面。可见,在弧状滑裂带的形成过程中,滑带的强度从峰值降低到残余值,这是地连墙槽壁整体滑动渐进形成过程中滑裂带强度的演化特征。

图1 含承压水的双粉砂层槽壁渐进破坏示意
1.2 考虑渗流的强度折减法的基本原理
穿湖地层地连墙成槽施工,围堰外侧水位较高,产生的渗流力对槽壁作用较为明显,因此,有限元模拟中必须要考虑渗流场作用。而实际中,土体渗流场和应力场之间是相互联系、相互影响的,其实质为应力场作用于土体上,使土体变形,从而改变土体的渗流特性,渗流场因此发生变化,渗流场的变化又会导致水头分布的改变,使土体的有效应力和作用在土体的渗流力发生改变,即应力场发生改变[10]。因此,为了分析稳定渗流下槽壁稳定性,必须考虑渗流和应力的耦合。ABAQUS软件可以对土中水的渗流和土体应力进行耦合分析,孔隙水的模拟主要由渗透系数和孔隙比来设置,而静水压力作用通过设置浸润面和底面的孔隙压力从而自动生成线性分布孔隙水压力,两层承压水层应进行分段设置孔隙水压力。
强度折减法在ABAQUS中的实现主要通过对土层塑性参数属性进行场变量设置,通过场变量中多组折减系数的设置来进行有限元强度折减,具体折减过程是将地连墙所在土层抗剪强度参数c,tanφ同时除以一个试算的折减系数Fr,得到一组新的cm、φm值,然后将其作为新的参数代入有限元进行试算,反复多次,直至槽壁土体符合给定的临界破坏状态判别标准时,对应的Fr即为槽壁的稳定性安全系数。其中,参数cm、φm分别由以下两式求得,即
cm=c/Fr
(1)
φm=arctan(tanφ/Fr)
(2)
1.3 槽壁失稳的判断准则
强度折减法的判断准则最早是在判断边坡失稳中诞生的,之后在边坡和基坑中得到广泛应用[11-13],就方法而言,判断准则在地连墙槽壁失稳中也同样适用,目前用于失稳判据大致可以分3类:①收敛判据。折减后的土体强度参数使得有限元计算在规定的迭代次数内不能收敛。②位移判据。当折减系数增大到某一特定值时,槽壁位移会发生突变,即可认为槽壁已经失稳破坏。③塑性区判据。通过对有可能发生破坏的区域内广义剪应变等物理量的变化和分布来判断,当塑性区从槽壁深处某一位置贯通至地面。目前,位移判据和塑性区判据应用最广,位移判据可以清晰得出槽壁的稳定安全系数,而塑性区判据可以清晰看出滑裂面的位置和形状,能很好反映出渐进破坏演化过程。为了全面准确地分析槽壁破坏过程以及得出安全系数,本文依据位移突变和塑性区贯通判断准则对槽壁稳定性进行综合判断。
2 有限元模型计算
2.1 工程背景
为了研究地连墙穿越双粉砂层在承压水作用下的成槽破坏模式及破坏过程,本文依托苏州春申湖路快速化改造工程进行有限元模型计算。该工程以明挖隧道形式由西向东穿越阳澄西湖,湖中段基坑施工长度为2 685 m,基坑深度10.54~18.17 m,隧道采用围堰明挖法,围堰采用拉森钢板桩进行隔水施工,抽水变陆地后在湖底施工,现场施工和地质分布见图2。湖中段基坑围护结构采用地下连续墙,由于在湖中进行地连墙成槽施工,地下水较为丰富,潜水位位于地下2 m,且在④2粉土夹砂层和⑥3粉土夹砂层分别存在微承压水和承压水,微承压水头标高为1 m,承压水头标高为-2 m,地连墙在进行成槽开挖时很容易发生塌槽现象,给工程质量安全和成本控制带来极大挑战。

图2 春申湖明挖隧道现场情况
2.2 数值模型
本文采用有限元软件ABAQUS对春申湖隧道地连墙成槽施工进行数值模拟,基于对称原理,可以将现场地连墙进行简化,按现场实际1/4尺寸建立三维数值模型,考虑到模型的边界尺寸效应,三维模型尺寸取60 m×60 m×90 m,依据据现场实际地连墙长度、厚度和深度,模型中分别取3、0.6、45 m。有限元网格划分如图3所示,模型采用孔隙流体/应力耦合的C3D8P八节点六面体单元,土体采用Mohr-Coulomb屈服准则模型,导墙采用弹性单元,模型侧面边界约束水平位移,底面边界约束水平和竖向两个方向的位移,上表面为自由面,孔压边界条件为侧面和底面默认为不透水面,水位浸润面孔压设为零,底面孔压根据浸润面以下土层深度呈现线性分布,但由于粉砂层中存在承压水,需对潜水层和承压水层进行分段设置孔压,从而更准确地模拟现场实际的孔隙水压力分布。

图3 有限元网格划分(单位:m)
根据实际地质勘测,沿线场地地表下90.3 m深度范围内地基土构成除填土外,其余为第四系滨海、第四系河泛、河床相沉积物,一般由黏性土、粉(砂)土组成。计算模型的土层物理力学参数信息见表1。

表1 土层物理力学参数
3 数值结果分析
3.1 有限元渗流场分析
成槽开挖前沿深度方向的孔隙水压力分布见图4a,由于该地层中在上粉砂层和下粉砂层中存在微承压水和承压水,且微承压水头为1 m,而承压水头为-2 m,和潜水面齐平,故图4a中微承压水层孔隙水压力比邻近层凸出一部分,说明该层水压力比邻近层的孔隙水压大,而承压水层无突变。地连墙成槽开挖后的孔压等值线云图见图4b。由图4b可知,此时槽壁渗流的浸润面即为孔压为0的分界面,开挖后地连墙附近孔压分布呈现漏斗状。

图4 沿深度孔隙水压力分布
土体开挖过程中孔隙水有效速度矢量见图5a,由图5a中可知,孔隙水流主要集中在槽壁底端附近,说明渗流力在槽壁底端出现集中现象,在下粉砂层出现流线聚集,且流线较长,流线由槽壁外侧向槽壁内侧移动,由此说明该土层流速过快,产生的渗流力较大,对槽壁的冲击较大,而该土层渗流力较大是由于粉砂层渗透系数较大,且靠近槽段底端。下粉砂层底端处孔隙水有效渗透速度随折减系数变化见图5b。由图5b可知,下粉砂层有效渗透速度随着折减系数的增加而增加,增长曲线呈现线性增长,当折减系数依次增大,土层的抗剪强度随之降低,土层塑性破坏程度越来越大,导致土层中孔隙占比增大,渗透系数也随之增大,孔隙水的有效渗透速度将相应增大。由此说明,应力场和渗流场是相互影响的,强度折减不仅会降低土层的抗剪强度,也在一定程度上改变土层的渗透系数,造成渗流力作用更加明显,从而加速粉砂层局部破坏进程。

图5 孔隙水有效速度分布及变化
3.2 槽壁失稳渐进破坏模式分析
图6为双粉砂层地连墙槽壁在承压水作用下塑性区破坏演变过程图,从图6可以看出,有限元强度折减法能够真实地反映槽壁整体失稳滑动的破坏过程,通过对土层进行整体强度折减,塑性破坏区一开始出现于槽壁下粉砂层底部和上粉砂层,随着强度折减次数的不断迭加,塑性区不断由上下粉砂层向中间扩展增大,直到塑性破坏区重叠连通,由此槽壁出现大范围整体失稳滑动破坏,滑动破坏面最终呈现弓字状。塑性破坏区起于双粉砂层底部,由于粉砂层本身不太稳定,且渗透系数较大,在承压水作用下很容易出现塑性破坏,从图5a也可以清晰看出,当成槽开挖至槽底时,孔隙流体会出现流动现象,从而造成孔隙水压力重新分布,会在槽壁底部产生较大的渗流力,造成下粉砂层底部最先出现塑性区,而上粉砂层在微承压水作用下也会很快出现塑性区,由于双粉砂层起始小范围的塑性区会造成邻近土层抗剪强度不断被削弱,从而使塑性区不断向邻近土层扩展,塑性区不断延伸重叠,最终会连通双粉砂层,造成槽壁整体滑动失稳。其实,塑性破坏区一般起于薄弱土层,这里的薄弱土层包括两个方面,一方面土层自身抗剪强度参数较小,土层自身存在安全隐患;另一方面,土层所受外力过大,如渗流作用下的渗流力,会对土层产生很大的冲击作用,从而造成土层的不稳定性。由以上分析得出,地连墙槽壁稳定状态会随着时间的推移不断发生变化,槽壁失稳破坏会经历从局部失稳到整体失稳的破坏演化过程,稳定状态会经历稳定、欠稳定和不稳定三个过程。图7为槽壁下粉砂层底端水平位移随折减系数变化。由图7可知,在折减系数达到1.35时,位移发生突变,此时槽壁处于不稳定状态,往往容易发生局部失稳破坏现象,故槽壁稳定性安全系数为1.35。

图6 塑性破坏区发展过程
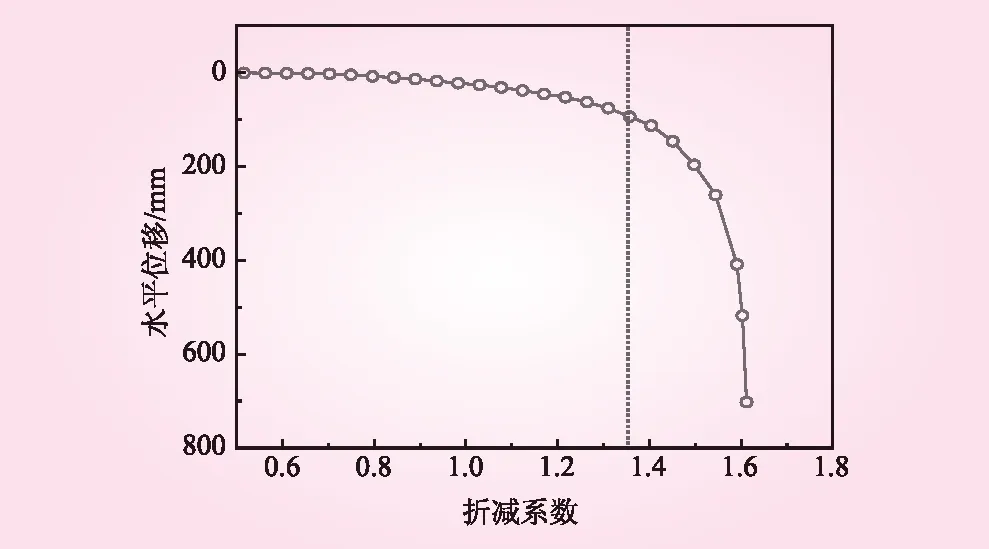
图7 水平位移随折减系数变化
3.3 双粉砂层开挖相互耦合影响分析
不同开挖深度下粉砂层等效塑性应变云图见图8。由图8可知,开挖15 m时,经过不断的强度折减,槽壁会在粉砂层最先出现局部塑性破坏区;开挖45 m时,在经过多次重复强度折减下,槽壁会在双粉砂层出现明显的塑性破坏区。两种工况下上粉砂层的等效塑性应变对比见表2。由表2可知,两种工况下粉砂层塑性应变趋势基本一致,最大的塑性应变都是出现在粉砂层底部,且随着下粉砂层的开挖会对上粉砂层的塑性应变产生一定影响,粉砂层顶部塑性应变由0.12变为0.27,变化幅度较小,而粉砂层底部由0.67变为7.65,变化幅度较大,由此说明,下粉砂层开挖会对上粉砂层产生一定的影响,且对粉砂层底部塑性应变比顶部影响大。综上所述,粉砂层相比于其他黏性土层对土体强度折减更为敏感,在土体强度不断折减降低的条件下,更容易发生槽壁失稳破坏。

图8 不同开挖深度下粉砂层等效塑性应变云图

表2 不同开挖深度下上粉砂层等效塑性应变
3.4 开挖深度对槽壁安全系数的影响
考虑渗流和不考虑渗流作用时槽壁安全系数随开挖深度变化见图9。由图9可知,两种曲线下,考虑渗流作用比不考虑渗流作用下的曲线整体偏下,说明渗流作用对成槽开挖中槽壁稳定性影响较大,考虑渗流作用时,实际工程中对高水位区的成槽开挖一定要严格控制地下水位造成的渗流影响,尤其在对承压含水层地连墙成槽开挖,一定要采用减压降水措施。此外,随着成槽开挖深度的不断增加,槽壁稳定性安全系数会下降很快,当开挖深度为15 m时,稳定性安全系数为1.61,开挖深度为45 m时,稳定性安全系数下降至1.35,降幅达16.1%。由此可见,开挖深度对地连墙成槽开挖影响较大,实际工程中对于超深地连墙的开挖一定要严格控制成槽施工对槽壁土体造成的扰动影响。

图9 槽壁安全系数随开挖深度变化
3.5 现场声波实测对比
为了验证数值分析结果的准确性,本文选取对应地层抓槽试验和正式成槽开挖的声波实测图和数值模拟结果进行对比分析,由于抓槽试验开挖了15 m,故数值结果选取开挖15 m时槽壁等效塑性等值云图作为对比参照。数值模拟与声波实测对比见图10。

图10 数值模拟与声波实测对比
从图10a可以看出,成槽开挖15 m数值模拟云图中塑性应变等值线主要集中分布于④2粉土夹砂层,显示出塑性破坏区主要出现在粉土夹砂层中,声波实测图表现为在④2粉土夹砂层中发生局部塌孔现象,这是由于粉土夹砂层本身不稳定,渗透系数较大,在微承压水的作用下容易发生渗透破坏,从而造成局部塌孔。
从图10b可以看出,不考虑微承压水的条件下成槽开挖45 m时,数值结果并未出现图8b中两层明显塑性破坏区,而正式成槽开挖声波实测也只在下层粉土夹砂层出现大面积塌槽,而上层粉土夹砂层并未出现明显塌孔,这是由于在此前进行了抓槽试验,得出微承压水是造成粉砂层塌孔的主要原因,正式施工前采用减压降水措施,降低了微承压水头,从而提高了④2粉土夹砂层的成槽稳定性。实际上,强度折减下的槽壁塑性破坏区范围往往比现场声波实测显示的粉砂层局部塌孔的要大很多,因为现场声波实测只是整体强度折减下出现整体滑动的前期局部破坏某一阶段,并不是强度折减下计算不收敛的最终结果,在这一局部阶段,数值分析结果表现为槽壁局部小范围塑性区破坏,声波实测结果表现为粉砂层局部塌孔或整层失稳塌槽。经实测对比分析所得,数值模拟结果和声波实测基本吻合,既验证了数值模拟的准确性,也揭示出粉砂层在承压水作用下较其他黏性土层更容易发生局部塑性失稳的事实。
4 结 论
本文开展渗流作用下双承压含水层地连墙成槽开挖的数值模型分析,通过强度折减法对地连墙破坏模式和槽壁稳定性进行研究,主要得到以下结论:
(1)考虑渗流作用的粉砂地层地连墙成槽开挖,渗透系数较大的粉砂层渗透速度较大,所受渗透力较大,容易发生渗透破坏,且粉砂层有效渗透速度会随着土体强度折减系数的增加呈现线性增加趋势,说明土体的应力场与渗流场存在相互影响,粉砂层局部失稳破坏往往是由于土体强度降低和渗透力增大综合影响产生的。
(2)确定了渗流作用下双承压含水层在成槽开挖中的破坏模式,在双粉砂层底端最先出现塑性区,随后塑性区由双粉砂层不断向中间扩展,最后双粉砂层会连通形成贯通的塑性滑裂带,滑裂面形状最终呈现弓字状,槽壁整体滑动失稳往往是由于粉砂层局部失稳造成的。
(3)地连墙成槽开挖对双粉砂层等效塑性应变存在相互影响,随着下粉砂层的开挖会导致上粉砂层等效塑性应变增大,且对粉砂层的影响表现为上部影响小,底部影响最大。此外,考虑渗流作用时槽壁稳定性系数整体会比不考虑渗流作用时大,随着开挖深度的不断增大,槽壁稳定性安全系数会不断降低。
(4)结合实际工程的声波实测结果进行对比分析,数值计算结果和声波实测较为吻合,从而一定程度上验证了数值模拟的准确性,也更好地揭示了粉砂层在承压水作用下较其他黏性土层更容易发生局部塑性失稳的事实。
