旋转机器人手臂奇异位形分析

费 雄，张 宇，孙伟栋

（昆明理工大学机电工程学院，云南昆明 650500）

0 引言

近年来，机器人技术发展日新月异，在工业等许多领域都发挥着不可替代的作用，人们对机器人机构问题的研究也越来越深入。对于任何机器人机构而言，都会存在一种非常特殊的位姿形态，即机构的奇异位形。从机构发明之初，奇异性问题就已随之而来。机械臂可能会发生奇异位形的情况大致可分为以下两种：机械臂工作空间内部奇异位形与机械臂工作空间边界奇异位形［1］。当工作空间内部发生奇异位形时，会导致机器人灵活性变差，瞬时丧失应有的自由度，无法进行运动，引起机构锁死，可能导致失控的问题，这种情形一般是由两个或两个以上关节轴线共线引起的；当工作空间边界发生奇异位形时，机械臂、机械手各个关节一般都处于完全伸展开来的形态，或处于与先前相反，即完全收回的形态，这两种形态都会使机械臂末端执行器处在一个十分接近机械臂工作空间边界的极限位置形态。针对这种情况，通常只需机构在运动过程中，尽量避免接近该工作空间的极限位置，即可规避此类奇异位形的发生。因此，针对机器人机构奇异性问题开展相关研究是非常必要的，对于提升机器人工作性能以及规避故障可提供重要的理论根据。

对于机械臂而言，奇异位形是机械臂一种十分特殊的运动特性［2］。针对机器人机械臂的奇异性问题，国内外学者进行了许多理论研究。现阶段关于机械臂奇异性问题的相关研究理论主要有以下几种：线几何理论［3-4］、旋量理论［5］以及代数理论［6］。刘满德等［7］最早对机器人奇异性问题展开研究，并引进雅克比矩阵的奇异鲁棒逆在奇异点周围提供可行、连续的解；胡准庆等［8］针对机器人奇异问题，对形态各异、类别不同的几种机器人进行对比研究，从而获得更精确的数据结果；李诚等［9］运用微分变换方法，以某款胶装机器人为研究对象，分析求解该机器人对应的雅克比矩阵，并以此数学矩阵为基础对该机器人进行对应的奇异性分析，从而获得该胶装机器人在工作过程中所有可能会出现奇异位形的情况；张新等［10］以一款反恐排爆功能机器人的5 自由度机械臂作为研究对象，分析获取该机械臂对应的雅克比矩阵，并对该机械臂奇异问题进行分析；CHENG 等［11］则对一款具有6 个自由度的PUMA 类型机器人进行奇异性问题研究，并求得该机器人的奇异构型情况；NOKLEBY［12］针对某款具有7 个自由度的加拿大臂进行奇异问题分析，同样也获得了该机械臂的所有奇异构型情况；史士财等［13］以某款具有7 自由度的机械手臂作为研究对象，采用旋量抑制方法对该机械手臂进行分析，进而求出与该机械手臂相关的几何特征及可能出现的奇异形态；BOHIGAS 等［14］提出一种基于数值计算的分析方法对并联机构及平面连杆进行奇异问题分析。

本文首先对传统机构运动模型创建方法进行分析研究，然后对传统四元素D-H 参数通用法进行改进，运用改良后的五参数D-H 方法［15-16］针对旋转机器人机械臂建立对应的连杆坐标系，以及相应的运动学模型，从而求得对应的正逆解，并进行仿真与验证工作。在雅克比矩阵求解方面，本文在传统矢量积分法基础上同时运用微分变换法，两种方法相辅相成，大大节省了计算时间，十分方便、快捷。

1 运动建模与分析

本文主要以项目小组自行生产的某一款旋转机器人的机械手臂作为研究对象。该旋转机器人机械手臂整体工作结构以及工作平台如图1 所示。

Fig.1 Rotating robot arm图1 旋转机器人机械手臂

根据机器人机械手臂所对应的D-H 参数，可建立与该机械臂对应的坐标系图，如图2 所示。

Fig.2 Rotating robot arm coordinate distribution图2 旋转机械臂坐标分布

旋转机器人机械手臂各连杆几何参数，以及各个关节之间对应角度等相关数据如表1 所示。

Table 1 Rotating robot manipulator related D-H parameters表1 旋转机器人机械手臂相关D-H 参数

根据上述机械手臂相关参数，可求得旋转机械臂各连杆变换矩阵如下：

由于机械臂末端执行器相对第i 连杆的位姿矩阵是已知的，如式（1）所示。

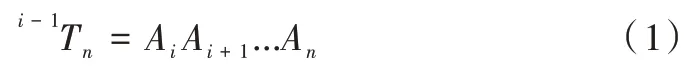
根据上述公式，可求得旋转机械臂末端执行器的位姿矩阵，如式（2）所示。

在机械手臂正运动学分析研究中，只需知道各个关节角度，再根据上述D-H 参数表中的相关参数，即可求出机械手臂末端位置及姿态。而且，对于同一个末端姿态点，也许是由不同关节组合而成的，具有多对单的映射关系，因此对机械臂进行正运动学分析会相对容易。因此，可利用MATLAB 分析软件的辅助模块ROBOT TOOLBOX，针对该旋转机器人机械手臂样机搭建数学模型［17］，并以该模型为基础进行正运动学模拟仿真。该旋转机器人机械手臂仿真模型如图3 所示。

Fig.3 Robotic arm simulation model图3 机械手臂仿真模型

运用MATLAB 仿真软件对旋转机器人机械手臂进行模型搭建，并对模型进行仿真分析，以及进行相应的正运动学求解［18］。仿真分析结果如图4 所示。

Fig.4 Simulation analysis results图4 仿真分析结果

其中，JOINT_B 表示各关节初始值，而P 表示初始JOINT_B 对应的机械臂末端位姿，以便于后续分析工作。

2 机械臂雅克比矩阵求取

对于旋转机器人机械手臂雅克比矩阵的求解，可选择简洁明了的矢量积法［20］，具体计算方式如式（3）所示。

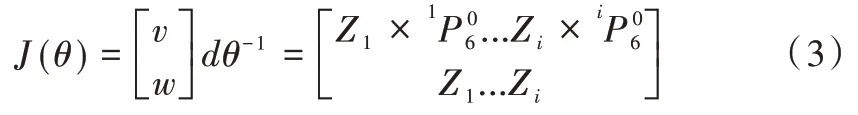
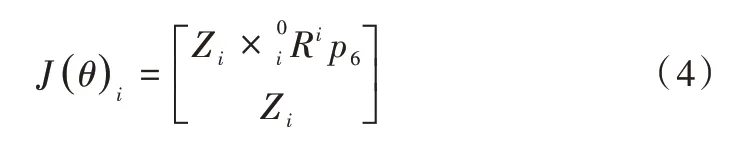
根据以上关系式，可变换解析得到机械手臂的雅可比矩阵表示式，如式（5）所示。

若想运用以上公式求取雅可比矩阵，需依次求出Zi、。矢量积法分别从角速度与平移速度两方面进行求解，其在表达方面非常清晰明了，且通俗易懂，便于后续求解。

机械臂的雅克比矩阵是机械臂关节速度与末端笛卡尔速度微分运动之间关系的一种数学表达，若更深入研究，则可解释为机械手关节基坐标系与尾端坐标系两者之间的微小动作关系，故可利用微分变换法［21-22］解析其之间的运动关系。基坐标系的细微运动引起末端位姿变化dT，即：

上述公式可通过数学变换，变形如式（7）所示。

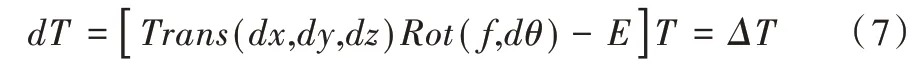
式中，dx、dy、dz 分别表示沿各坐标轴的平移量，dθ表示旋转角度，f 表示旋转轴矢量，然后将其代入相关公式中，可得：

其中，有：

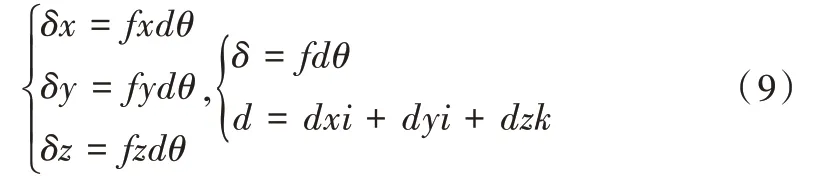
假如机械臂末端坐标系有微小变化，可设机械臂末端位姿变化为TdT，即：

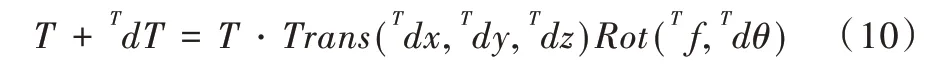
可将以上公式整理变换得到式（11）。

根据式（8）与式（11）可知同一位姿变化，则机械臂对应基坐标与末端坐标两者之间的微分运动是等价的，因此有对应关系式dT=TdT。代入相关公式，可得式（12）。

在运用D-H 法搭建的对应坐标系中，Z 轴方向表示关节轴线f 的方向。因此，对于机械臂的转动关节i，有旋转量δi=[0 0 1]Tdθi，平移量Td=[0 0 0]T。对于平移关节j，有δi=[0 0 1]Tdθi，δj=[0 0 0 ]。代入式（12）即可得连杆到末端坐标平移变换与末端坐标旋转的雅克比矩阵列矢量表达公式：

利用式（11）可求出最后一个关节的雅克比列矢量，与之对应的变换矩阵为：

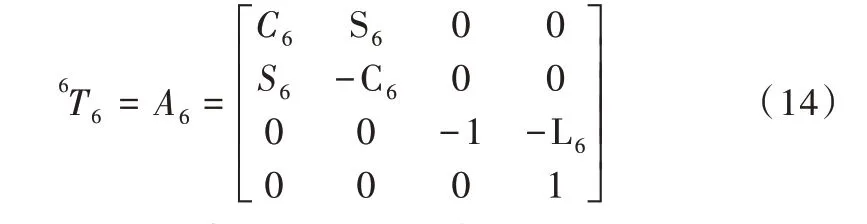
然后分别将对应参数n、o、a、p 代入关系式，即可解析出相应的雅克比矩阵列矢量：J6=[0 0 0 0 0 -1]T。

对于5 号关节，可在A6基础上求得其对应变换矩阵表示式为：

由于格式限制，机械手臂1 号关节与2 号关节的列矢量结果不便于在文中展示，其求取方法同上，故也可求出其雅克比矩阵表达式为：

3 奇异位形识别及仿真

虽然各类机器人与机械手臂的形态构型各异，但机械手臂每一个关节都有其对应运动区间，以及有效的工作边界与范围。因此，在这些极限边界范围处即可能产生关节的运动极限位姿，即奇异位形。此次试验的旋转机器人各个关节有效运动范围如表1 所示。

因此，当机械臂对应关节处于θ1=±170°、θ2=180°/65°、θ3=-170°/190°、θ4=±180°、θ5=±135°、θ6=±360°这些极限角度时，此时对应点应为极限位置奇异点。对于每一个奇异点，可利用MATLAB 并采用ROBOT TOOLBOX工具箱进行机械臂的三维图形仿真分析。各关节在极限位置的三维仿真图如图5-图10 所示。

Fig.5 No.1 joint limit position图5 关节1 极限位置

Fig.6 No.2 joint limit position图6 关节2 极限位置

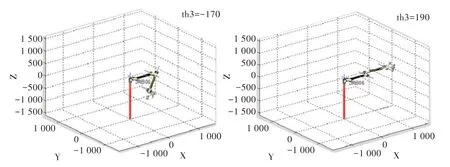
Fig.7 No.3 joint limit position图7 关节3 极限位置

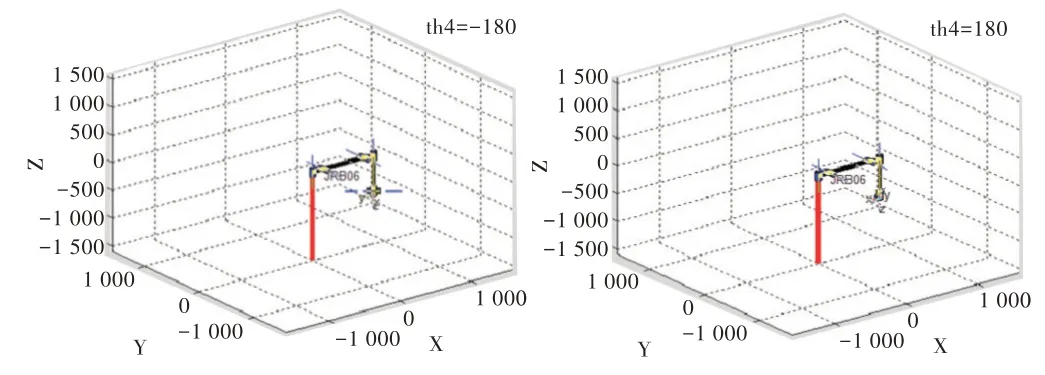
Fig.8 No.4 joint limit position图8 关节4 极限位置

对于第二种奇异位形情况，即工作空间内部奇异，由于奇异点根据雅克比矩阵的逆运动学求解会出现失效情况，因此可根据雅克比矩阵对内部奇异进行分析求解。由先前求得的雅克比矩阵表达式对旋转机器人可能存在的内部奇异位姿进行求解，最后运用MATLAB 对相应奇异位姿进行仿真得出三维图形。

Fig.9 No.5 joint limit position图9 关节5 极限位置

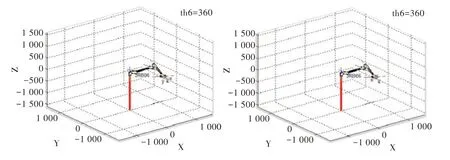
Fig.10 No.6 joint limit position图10 关节6 极限位置

由所得的雅克比矩阵关系式计算该矩阵行列式det(J(θ))，如式（19）所示。

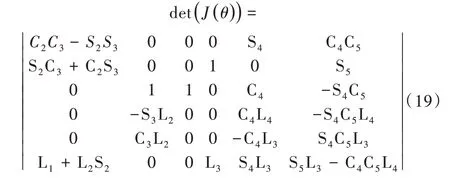
对公式进行行列式化简，并令行列式等于零，变换结果如下：

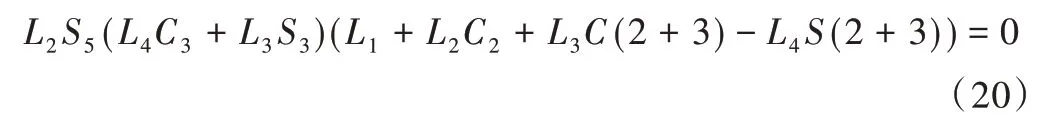
因为L2、L3、L4为机器人机械手臂机构所给定的连杆长度，或连杆偏移量不为零，所以假如需要上式等于零的条件成立，则可能有以下3 类情形，具体如下：

（1）当S5=0，也即sinθ5=0，此时θ5=kπ，则可知在5 号关节角度等于0 时，该机械臂机构会出现腕部的奇异情形(-2.356 2 ≤θ5≤2.356 2)。此时，可运用MATLAB 的机器人工具箱对该位置进行仿真分析，如图11 所示。

当5 号关节角为0 时，4、6 号关节轴线共线奇异如图12 所示。

（2）当L4C3+L3S3=0 时，在这种情形下，可对该公式进 行 变 换 得sin(θ3+β)=0，求 出θ3=arctan(L4L3)，其中L3不为零。由于L3=130，L4=638.7，代入公式可得θ3=1.370 0。将相关参数代入雅可比矩阵，利用SDV 算法对矩阵进行奇异值分解（采样点为60 个点），最后求出3 号关节角与雅可比矩阵最小奇异值的关系，如图13 所示。运用MATLAB 的机器人工具箱对该处的奇异形态进行模拟分析，如图14、图15 所示。

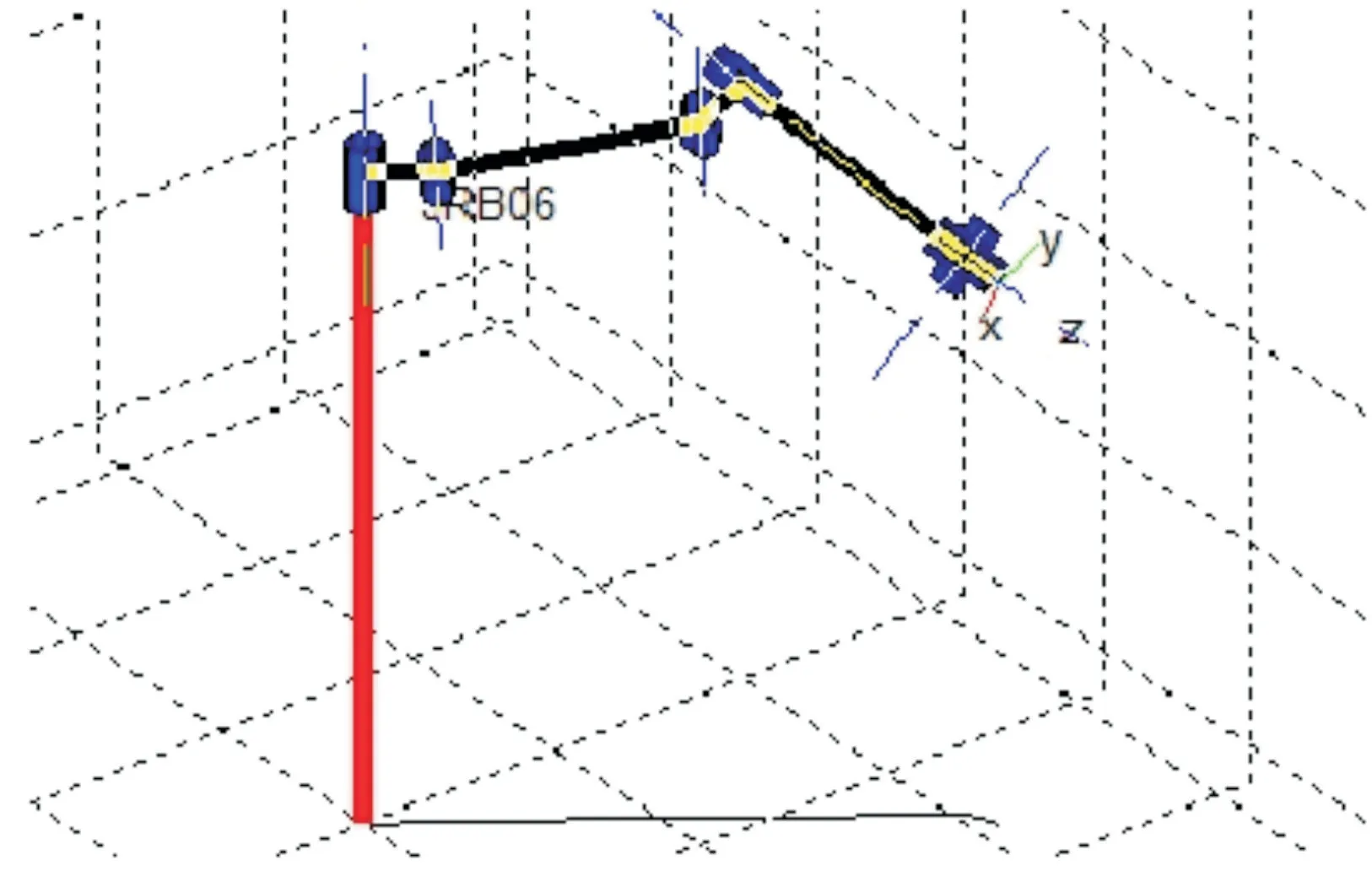
Fig.11 No.4，6 joints axis collinear singular simulation effect图11 4、6 关节轴线共线奇异仿真效果

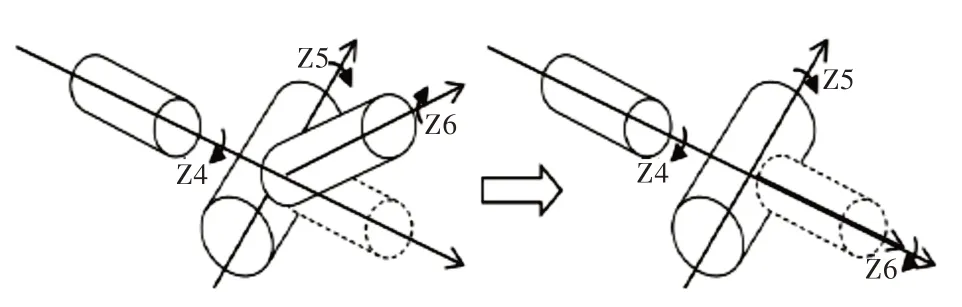
Fig.12 When the angle of No.5 joint is 0,the axis of No.4 and No.6 joints are collinear and strange图12 5 号关节角为0 时，4、6 号关节轴线共线奇异

Fig.13 The relationship between the No.3 joint and the smallest singular value of the Jacobian matrix图13 3 号关节与雅可比矩阵最小奇异值关系图谱

Fig.14 Simulation effect of singularity of No.3 joint图14 3 号关节奇异位形仿真效果

Fig.15 Simulation effect of singularity of No.3 joint and wrist图15 3 号关节与腕部组合奇异位形仿真效果

此时过机械手臂腕部的3 个关节分别为4 号、5 号、6号，腕部交点与2、3 号关节轴线处于同一直线上，如图16所示。

Fig.16 The intersection point of the wrist is on the same line as the axis of No.2 and No.3 joints图16 腕部交点与2、3 号关节轴线处于同一直线上

（3）当L1+L2C2+L3C(2+3) -L4S(2+3)=0 时，假如需要2 号关节与3 号关节满足该关系式，将会使对应雅克比矩阵行列式的值为0，从而导致机械手臂奇异位姿的产生。由于2 号关节与3 号关节两者关节轴线互相平行，因此对旋转机器人机械臂2 号关节、3 号关节角的限制条件简化如下：

由上述关系式可知，2 号、3 号两关节角度之间会形成一个奇异曲面，可运用MATLAB 对该曲面进行仿真。取满足上式关系的2 号、3 号关节值36.26、168.5，关节2、关节3 产生的内部奇异与腕部奇异组合仿真效果如图17 所示，而与上述情形（2）的奇异组合仿真效果如图18 所示。

Fig.17 The combined simulation effect of internal singularity and wrist singularity produced by No.2 and No.3 joints图17 关节2、关节3 产生的内部奇异与腕部奇异组合仿真效果

Fig.18 Simulation effect of singular combination between No.2 and No.3 joints wrist and situation (2)图18 关节2、关节3、腕部与情形（2）之间奇异组合仿真效果

综上可知，六关节旋转机械手臂主要可能存在3 种奇异位形（即腕部的4 号与6 号关节共线、3 号关节出现某个极限边界值、关节2 与关节3 在一定条件下发生内部奇异的情况），以及这3 种奇异情形之间的组合情况。

4 结语

本文以某款旋转机器人的串联机械手臂作为研究对象，首先采用D-H 参数法搭建该机械手臂的运动学模型，进而求得其正运动方程，同时根据机械手臂各关节对应参数值求解出该旋转机器人手臂基坐标系及机械手臂尾端位置信息；然后根据机械臂正运动方程构造与之对应的雅可比矩阵，进而求解出该机械手臂可能会发生奇异位形的所有情形；最后运用MATLAB 软件的机器人工具箱，对求解出的奇异位形情况进行模拟仿真分析，从而验证理论求解结果的正确性。

通过分析得到该旋转机器人机械手臂所有可能发生奇异位形的情形，主要存在3 种奇异位形，以及3 种奇异情形之间的组合情况。本文研究可帮助该旋转机器人机械手臂在执行工作任务过程中规避特殊的运动形态以避免出现奇异位姿，提供十分重要的理论分析数据，对机械臂后续研发工作具有一定的实际意义。