高强Q690钢柱高温下轴心受压局部稳定设计方法

王卫永 SHARHAN Ahmed AL-AZZANI Hisham 李翔

摘 要：局部屈曲是鋼结构构件的一种破坏模式，钢结构发生局部屈曲破坏时，屈曲应力小于钢材的屈服强度。为了研究高温下高强Q690钢柱的局部稳定性能，采用有限元软件ABAQUS建立有限元模型，模型采用其他学者完成的Q460钢柱轴心受压局部屈曲试验进行验证，考虑宽厚比、温度、初始缺陷、残余应力和翼缘与腹板之间相互作用的影响，对高强Q690钢柱进行参数分析。研究结果表明：宽厚比对局部屈曲有显著影响，宽厚比的增大导致试件极限承载力的降低;初始缺陷和残余应力对局部屈曲应力有较大影响，且试件的极限承载力随着温度的升高而明显下降。基于有限元分析结果提出了适用于高强Q690钢柱高温下的局部稳定设计方法和宽厚比限值，并与GB 50017-2017、Eurocode 3和ANSI /AISC 360-10中的设计方法进行了比较。

关键词：高强度钢;钢柱;局部屈曲;高温;有限元分析

1 Introduction

High strength steel （HSS） has been widely adopted in the construction of high-rise structures such as high-rise buildings and long-span bridges on account of its light-weight， with the result that these structures have become novel in shape and complicated in function. In this era of rapid development， steel structures have numerous benefits such as high strength， light-weight， fast construction， and good deformability. Steel construction is required to suit the quick development of the infrastructures and the world's economy. In addition， the use of HSS can greatly contribute to the reduction of the cross-sectional size of structural members， reduce the amount of steel and the weight of the structures， leading to the reduction of the work efforts of welding and transportation as well as inducing high resistance to earthquake effects. In general， the use of HSS in construction is good for the environment and saves time[1].

The advantages to the construction industry of adopting HSS such as Q690 steel have motivated researchers to study the performance of HSS compression members at ambient and elevated temperatures. Shi et al.[2] found that the local stability of an H-shaped member could be ensured by increasing the width of the steel plate. The width-to-thickness ratio of the steel plate in the H-section member should be larger than that of the mild steel， also known as low carbon steel， in order to make full use of the advantages of the strength of high-strength steel. Based on finite element analysis， Knobloch et al.[3] proposed a strain-based calculation method for the local stability of steel members at elevated temperatures. However， this method has not been verified by experimental results， making it risky to use in engineering. Wang et al.[4] suggested a calculation equation of the local buckling stress of Q235 and Q460 axial compression members at elevated temperatures where the limit of the width-to-thickness ratio was provided to restrict the local buckling of the member at elevated temperatures. Additionally， some compression tests were conducted on slender columns of welded sections with steel grades from 460 to 960 N/mm2[5-11]. The results showed that the sections with steel grades higher than 460 exhibited significantly higher buckling resistance than counterparts made of conventional steel types. The improved resistance can be attributed to higher yield strength and lower residual stress to yield strength ratios. It was also found that the end restraints and limited initial imperfections contributed to improvements in resistance. Chiew et al.[12] conducted an elevated temperature test to investigate the strength of reheated， quenched， and tempered （RQT） HSS at elevated temperatures. Post-fire residual strength was evaluated by means of post-fire residual strength tests. Li et al.[13] and Kang et al.[14] investigated the strength deterioration of high strength structural steel Q690 after fire. They found that the post-fire mechanical properties of the structural steel were significantly decreased when subjected to temperatures exceeding 600 ℃. Through these investigations on steel stub columns made of welded sections， it was concluded that the plate slenderness limits for yielding for conventional steel sections can also be applied to the steel sections made of high strength steel. However， sufficient deformation capacities cannot be guaranteed if the limits of plate slenderness for conventional steel compact sections were simply extended to high strength steel sections[15].

There are many international codes for the design of structural steel at ambient and elevated temperatures; however， the majority could only be applied to the low and intermediate grades of steel. The Chinese standard for design of steel structure （GB 50017-2017）[16] provides the limits of the width-to-thickness ratio of the steel plate for the local buckling of H-section members to ensure that no local buckling occurs before the overall buckling. However， the standard design provisions do not consider high strength steel. The Eurocode 3 （EC3）[17] generally includes a more reliable and safe design formula， which can be applied to the design of the local buckling capacity of high-strength S690 steel I-section members. The American steel structure design code （AISC 360-10）[18] provides slenderness limits to control local buckling for column strength， as expressed in Eq. （1） and （2）， where the slenderness limits （λp andλr） of thin-plate elements must be satisfied to prevent local buckling of the plate elements.

where，fy is the yield strength of steel; Es is the elastic modulus of steel.

In the EC3[17] provisions， a reduction factor of 0.85 is adopted for the elastic modulus and the yield strength to treat the local buckling phenomena of the steel element subjected to elevated temperatures. Conversely， the Chinese standard for the design of steel structures[19] as well as code for fire safety of steel structures in buildings do not include specifications and guidelines for the design of steel at elevated temperatures. Overall， the current design approach in codes including GB 50017-2017[16]， EC3[17]， and ANSI/AISC 360-10[18] is only applicable to steel with a yield strength of up to 460 MPa and could not be adopted for the design of HSS columns. Therefore， in practice， the application of high-strength steel members is restricted. However， EC3 Parts 1-12[20] extends its specification to steel grade up to 700 MPa. Furthermore， most steel design codes adopt an equivalent imperfection approach to consider the effects of residual stress and out-of-plane imperfections that is generally assumed to be 1% of the member length. According to the research by Li et al[21]， this equivalent value for residual stress would lead to unconservative predictions for high strength steel members. Based on the aforementioned points and on the FE modeling results， a simplified design method and new width-to-thickness ratio limits are proposed for the studied high strength Q690 steel stub columns with H-shaped section.

In this study， finite element modeling was performed using the software package ABAQUS to simulate the performance of high-strength Q690 steel H-shaped welded columns at elevated temperatures under axial compression. The numerical models were first adopted to replicate the experimental results carried out by Wang et al.[27]. Then， an extensive parametric analysis was conducted for the Q690 HSS welded columns. The effects of many parameters including the width-to-thickness ratio， temperature， initial imperfection， residual stress and interaction between flange and web on the behavior of the studied axially-compressed steel member at elevated temperatures were evaluated. The results of the parametric study were then compared with the results obtained from the design provisions in GB 50017-2017[16]， EC3[17]， and ANSI/AISC 360-10[18]. Based on the FE results， a new design method was recommended for local buckling design of high strength Q690 steel columns at elevated temperatures.

2 Material properties of high strength Q690 steel

The deterioration of the mechanical properties including the elastic modulus and yield strength is considered the main factor influencing the performance of steel structures in fire. As the temperature increases， the yield strength and elastic modulus of the steel are reduced. Wang et al.[22] obtained the mechanical properties of Q690 steel at elevated temperatures through a series of tensile coupon tests and proposed reduction coefficients for the nominal yield strength and elastic modulus of Q690 steel exposed to elevated temperatures. The tests results are summarized in Table 1 and depicted in Fig. 1， where the reduction factors for Q690 at elevated temperatures （20-900 ℃） steel can be obtained from Eq.（3） and （4）， expressed as：

where，fyT and fy are the yield strength of steel at elevated and normal temperatures; ET and E are the elastic modulus of steel at elevated and normal temperatures; Ts is the steel temperature. Fig. 1 depicts the comparison of the test results and the results obtained using the proposed equation of the reduction factors for yield strength and elastic modulus of Q690 steel at elevated temperatures.

Each type of steel has a particular chemical structure， and high temperatures may affect different material properties. The variations between high strength steel and mild steel in the reduction factors are shown in Fig.2. It can be seen that the stiffness and strength of mild steel are greater than those of high strength steel. This could be related to the variety of the components and formulations of the chemical elements and the differences in the manufacturing techniques. Test data on the reduction factors of yield strength and elastic modulus for mild steel SM41[23]， Q235[24]， and high strength steel with grades of S460， Q460， S690[25]， and Q690[22] were also compared.

3 Finite element modeling

This paper utilizes the finite element analysis software ABAQUS 6.14 to simulate the local buckling of high strength Q690 steel welded H-section columns at elevated temperatures under axial compression. The element section type， constitutive relationship， geometric imperfection， residual stress， and boundary conditions are used to build the FE model.

3.1 Element type， mesh， and material modeling

The proper selection of element type with appropriate degrees of freedom is essential to simulate the behavior of the stub columns. Various options are available in ABAQUS to model the steel structure. In this paper， the four-noded element quadrilateral S4R shell element with reduced integration， in which each node has six degrees of freedom， is adopted to represent the element type for the steel plate， where lateral shear and large strains are allowed. The number and quality of the finite element mesh directly affect the accuracy of the results and the computation time. Therefore， a suitable mesh is a necessary condition for obtaining accurate simulation results. Based on sensitivity study， the mesh size of the element between 12-20 mm was found suitable. The stress-strain response of the steel at elevated temperatures was simulated using the steel model proposed by Wang et al.[22] for the Q690 steel at elevated temperatures. The stress-strain relationship of the studied Q690 steel can be obtained as follows

where， σ0.01 andσ0.2 are the static tensile proof stress of 0.01% and 0.2%; m is the exponent for the modified Romberg-Osgood model given in Table 2; n is the strain-hardening exponent; n0 is the original strain-hardening exponent; K is the modular coefficient in the Romberg-Osgood expression; σu is the ultimate stress; εp is the plastic strain; εpu is the plastic strain at the ultimate strength.

3.2 Boundary conditions and load application

In order to appropriately apply the constraints and loads for simulating the rigid condition of the ends of the member， rigid endplates were set at both ends of the members. This step was performed as follows： the reference points were first set directly above the endplate and the degrees of freedom of all nodes of the endplate were rigidly connected with the degrees of freedom of the reference point using the constraint coupling command. Hence， rigid ends were generated at both ends of the element and the reference point became the loading point. Then， the contact surface between the steel column and the endplate was defined as the Tie constraint， so that the two surfaces were firmly bonded together to avoid separation during the analysis and achieve similarity with the actual welding. Therefore， it was similar to the actual test and it was possible to avoid local damage to the section of the element under the concentrated load.

The boundary conditions were fixed at both ends. The nodes at both ends were fixed against the displacement perpendicular to the axial direction and with no twist about the axial direction. The reference point at the top-end was fixed against displacement in all directions except for displacement in the axial direction， while the rotation was fixed in all directions except for a weak bending axis. The reference point at the bottom-end was fixed against the displacement and rotation in all directions. To ensure that the element was a statically indeterminate structure， the longitudinal displacement of one end of the element was restricted. The load was continuously applied according to the displacement control method. Because displacement control method easily converged， the calculation speed was fast， and the descending branch of the load-displacement curve could be obtained. The analysis type of the model was static risk analysis.

3.3 Residual stresses

The welding process is an uneven heating and cooling process and this uneven process causes residual stresses in the steel element. These residual stresses could adversely affect the ultimate capacity of the steel element. Therefore， residual stress is an important parameter， which needs to be considered in the FE modeling. Zhang[26] measured the residual stress of H-section Q690 steel and found that the measured distribution model was similar to that of mild steel section.

Based on the self-balancing principle of cross-section residual stress， the distribution width of residual tensile stress and residual compressive stress can be obtained. The distribution range of the H-section and the ratio of residual stress to the nominal yield strength of steel at ambient temperatures are summarized in Table 3 and 4， respectively. Fig.3 illustrates the distribution range of the residual stress of high strength steel H-section.

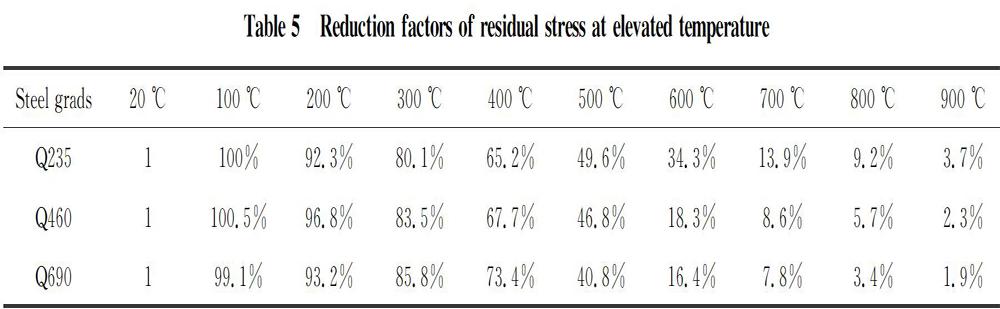
At elevated temperatures， the equation for predicting the residual stress reduction coefficient is reported in Reference [26]. The resulting expression is adopted to calculate the residual stress reduction coefficient for the H-shaped section of high strength Q690 steel as follows

As shown in Table 5， the reduction coefficient does not reduce significantly when the temperature ranges from 20 to 400 ℃. However， the residual stress reduction coefficient decreases obviously with the increasing of the temperature beyond 400 ℃. Conversely， the reduction coefficient significantly increases when the temperature increases from 500 to 900 ℃. It is also noted that no much reduction is observed for steel with different grades including Q235， Q460， and Q690 at elevated temperatures.

3.4 Verification of the FE model

The verification of the current model was carried out using the experimental program of local buckling of high strength Q460 steel stub columns tested under axial load conducted by Wang et al.[27]. A comparison of the FE results and the test results is shown in Fig.4（a）， where the load-displacement curves obtained from the FE model and the test data are illustrated. As shown in Fig.4（a）， the load-displacement curve obtained from the finite element model is in very good agreement with the load-displacement curve obtained from the test of the specimen. It can also be seen from Fig.4（a） that at the beginning， the load-displacement curves generated by FE model and test showed a slight variation and they continued smoothly during the whole elastic force-displacement stage until they reached the local buckling stress of the test specimen. A slight difference is observed in the descending branch of both the FE generated and the test load-displacement curve because it is very complicated to simulate the exact interaction effect between materials in the FE numerical model and the practical test specimen.

The failure modes of the specimen Q460-B-20 ℃ and Q460-B-650 ℃ steel columns， and a comparison of the column failure mode observed in the experiment with the failure mode obtained from the FE model is shown in Fig.4（b）. It can be seen that the failure model showed by the test fits well with that predicted by the FE model. Due to the position of the initial imperfections in the columns， there are some differences in the location of buckling and the imperfections will result in the first onset of local buckling.

4 The load bearing capacity of the high strength Q690 steel column

The design approach for predicting the axial compressive bearing capacity at elevated temperatures is based on the design method of axially compressed steel columns at normal temperatures.

Reference[19]provide an equation for calculating the critical stress of axially loaded steel members at elevated temperature， expressed as

where，σE，T is the Euler critical stress of the element at elevated temperature， which can be obtained by （σE，T=π2ET/λ2）， and e0 is the initial eccentricity of the elements， for the welded H-shaped， which can be obtained by （e0=0.300λ--0.035） in which， λ- is the slenderness ratio of the column and can be calculated by （λ-=λπ fyT/ET）.

The stability factor of the high strength Q690 steel column can be calculated using the following equation

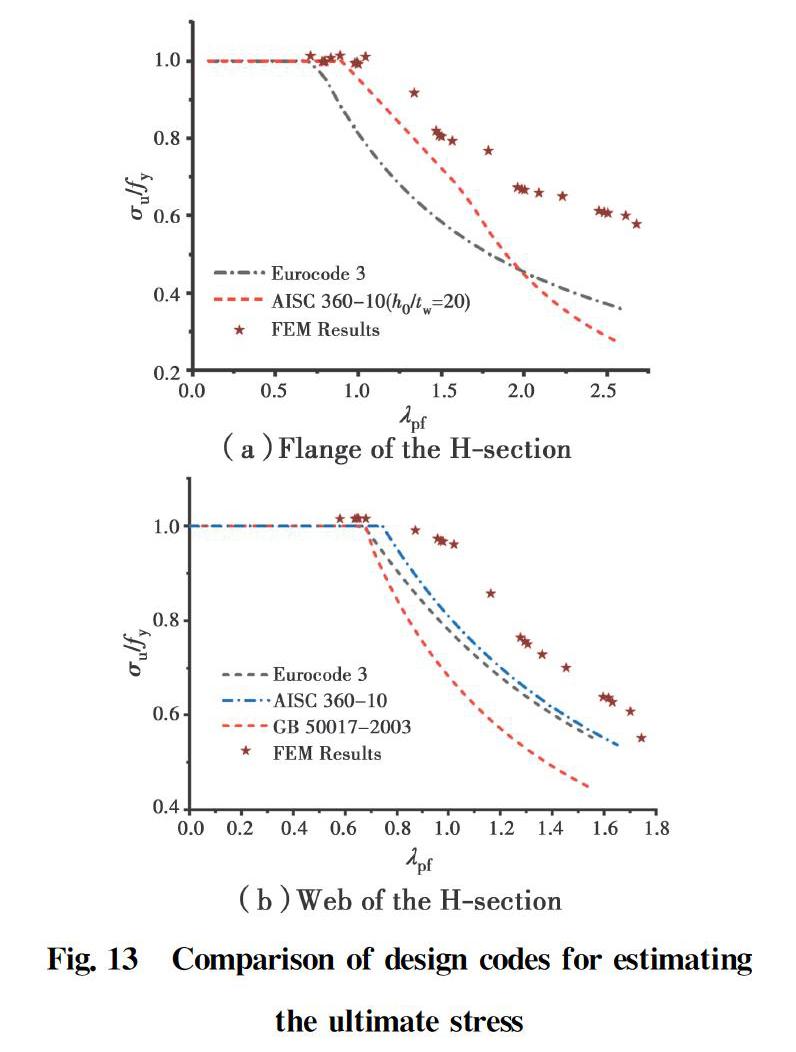
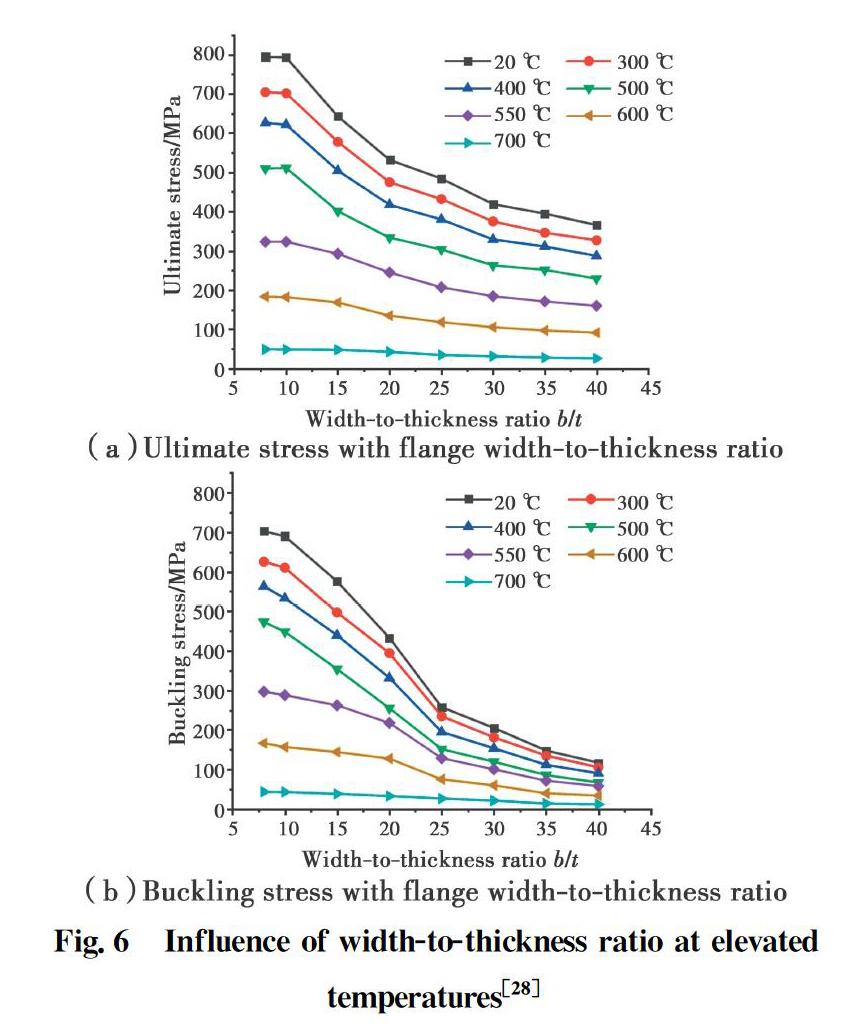
Fig.6（a） shows the ultimate stress versus the width-to-thickness ratio of the studied specimens at different temperatures. It can be seen that the ultimate stress can reach the yield strength when the width-thickness ratio decreases， whereas increasing the flange width-to-thickness ratio results in a reduction of the ultimate stress. The ultimate stress was also found to be reduced with the increasing temperature. Fig.6（b） shows the effects of flange width-to-thickness ratio on the buckling stress. The buckling stress decreases with the increasing flange width-to-thickness ratio as well as with the increasing temperature. Similarly， the web ultimate stress reduces with the increasing height-to-thickness ratio， as shown in Fig.7（a）. Additionally， the buckling stress of the web reduces with the increasing height-to-thickness ratio， as depicted in Fig.7（b）. When the temperature is between 20 ℃ and 550 ℃， the buckling stress decreases rapidly with the increasing plate width（height）-to-thickness ratio. When the temperature is than 550 ℃， the buckling stress decreases slowly with the increase of the width（height）-thickness ratio of the plate. In both cases， the width（height）-to-thickness ratio of the flange or web of the studied specimens significantly influence the ultimate stress and buckling stress of the studied specimens at elevated temperatures.

5.2 Interaction of web and flange

When the web or flange of the H-section of the steel member is partially buckled， the buckling stresses occurring in the two elements are not equal. Therefore， the buckled part can be constrained by the unbuckled part. In the engineering design， the H-shaped section of steel consisted of thinner web and thicker flange plates. Consequently， when the flange plate buckled first， the web had a limited effect on the flange plate， hence the restraining effect of the web on the flange can be ignored. On the contrary， when the web plate buckled first， the restraining effect of the flange on the web cannot be ignored. In this investigation， only web buckling is taken， so the restraining effect of the flange plate on the web is considered. Fig.8 depicts the variation of the ultimate stress versus the flange width-to-thickness ratio at elevated temperatures， where the web height-to-thickness ratio is kept at 30 mm. In order to ensure effective constraining effects of the flange on the web when determining the width-to-thickness ratio of the flange， the buckling stress of the web should be greater than that of the flange. As a result， the buckling stress of the web can be attained before the flange is buckled. It can be seen from Fig.8 that when the flange width-to-thickness ratio is 6， the web buckling stress is about 625.1 MPa and with increasing the width-to-thickness ratio of the flange to 20， the web buckling stress is found to decrease to 533.54 MPa， which is a decrease of approximately 14.7%. Similarly， at temperatures of 400～650 ℃， when the flange width-to-thickness ratio increases from 6 to 20， the buckling stress decreases by 17%. Overall， whether the axial compressive steel members are loaded at ambient or elevated temperatures， the retaining effects of the flange on the web should be considered when estimating the web buckling stress.

5.3 Initial geometrical imperfection

The initial imperfection of the steel plate is a key factor， which greatly impacts the ultimate bearing capacity of the steel columns. Fig.9 elucidates the local buckling stress of members with different geometrical imperfections. It considers the initial geometrical imperfection of 0.1t （t is the plate thickness）. According to the research results of Burgess et al.[29]， the thermal expansion of the element at elevated temperatures has little effect on the initial geometric imperfection of the steel element and hence it can be considered that the geometric imperfections at normal temperatures and elevated temperatures are similar. The Chinese code for check & accept specification for steel structure[30] stipulates that the initial geometric imperfection amplitude of the element is 1% of the flange plate gross width. Kaitiala et al.[31] adopted an initial imperfection range similar to that in [30]. The results of buckling stress versus the width-to-thickness ratio of FE models are compared with the calculated ones and it can be observed that both results have good agreement. Hence， the initial imperfections can be used to analyze the buckling stress of the steel specimens.

6 Simplified design method

6.1 Local buckling stress at elevated temperatures

The local buckling stress coefficient φ can be obtained from Eq.（11）， while the slenderness ratio （width-to-thickness ratio） of the steel plate can be calculated from Eq.（12）， expressed as

where， fyT is the yield strength of the steel at elevated temperatures， ET is the modulus of elasticity at elevated temperatures， k is the local buckling coefficient related to the boundary conditions. For flange buckling k= 0.425， for web buckling k=4， v is Poisson's ratio of steel v= 0.3.

Fig.10 illustrates the relationship between the coefficient of local buckling and the slenderness ratio （φλ- curves） at elevated temperatures. It can be seen from Fig. 10 that at elevated temperatures， the local buckling coefficient φ decreases with the increasing slenderness ratio （width-to-thickness ratio） and vice versa. It is also found that when the temperature is between 300 and 700 ℃， the curves are very close. These curves can be used to describe the φλ- relationship.

Based on the buckling stress results obtained by finite element analysis， the equation for calculating the local buckling stress of the member between 300 ℃ and 700 ℃ was obtained using data fitting analysis. For any H-shaped section， the local buckling stress of the member can be calculated by Eq.（13）.

The Q690 axial compression members at elevated temperatures are

where， λ- is the regularized width-to-thickness ratio of the plate， which can be calculated according to Eq.（12）. In order to verify the reliability of the calculation results of the fitting equation， the buckling stresses calculated by Eqs. （13） to （17） are compared in Fig. 11. For the Q690 axial compression member， the results obtained from Eqs. （15） to （17） are lower than the FE generated results.

6.2 Width-to-thickness limit

To ensure that the steel member at elevated temperatures

under axial compression satisfies the requirements of local buckling， it is important to select appropriate width（height）-to-thickness ratios of both web and flange elements. The relationship between the width（height）-to-thickness ratio and the slenderness ratio should be obtained through equaling the ultimate stress with the local buckling stress and the ultimate stress with the overall buckling stress of the steel element at elevated temperatures. Here， the relationships between the flange width-to-thickness ratio and the web height-to-thickness ratio with the slenderness limits can be expressed， respectively， as

GB 50017-2017[16] provides the limit values of the web height-thickness ratio and the flange width-to-thickness ratio of axial compression members at ambient temperatures as follows.

Fig. 12 compares the results of the width-to-thicknessratio and the height-to-thickness ratio with the slenderness limits at normal and elevated temperatures for the flange and web， respectively. In both cases， when the slenderness ratio of the specimen is less than 25， the limit value of the height-to-thickness ratio of the web at elevated temperatures is less than the limit of the height-to-thickness ratio at normal temperatures， while when the slenderness ratio of the component is greater than 25， the plate height-to-thickness ratio limit is larger than that at room temperature. This means that when the length of the element is relatively small， the element at high temperature is more likely to undergo local buckling， whereas， when the length is larger， the element at normal temperature is more likely to undergo local buckling.

7 Existing international codes of practice

7.1 Assessment of international codes

The assessment of the suitability of the current code of practice in designing the studied specimens is conducted through comparison with the FE-generated results， as shown in Fig.13， where the width-to-thickness ratio of the flange and the height-to-thickness ratio of the web are plotted against the slenderness limit in Figs.13（a） and （b）， respectively. From Fig.13 （a）， it can be seen that GB 50017-2017 provided a more safer estimate for the ultimate stress of the H-shaped section of the web than both Eurocode 3 and ANSI/AISC 360-10 in predicting the ultimate strength， due to their higher design values than the Chinese standard. However， as shown in Fig. 13 （b）， when λpf was smaller， the curves obtained from the design codes showed close results with FEM results， especially for the flange connected with quite a slender web. In addition， all design curves obtained from the standards became highly conservative when λpf was relatively large.

8 Conclusions

This paper utilized the ABAQUS finite element model to obtain the local buckling behavior of the welded H-section of high strength Q690 steel columns under axial compression. The FE models were first verified against experimental results. An extensive parametric study was conducted using the verified FE model over a wide range of parameters including elevated temperature， width-to-thickness ratio of flange， and height-to-thickness ratio of web， residual stress， and initial imperfections. A comparison with existing codes of practice was conducted to assess the suitability of current codes in predicting the compressive capacities of the studied specimens. A new design method was proposed. Based on these data， the following conclusions were drawn：

1）At elevated temperatures， the elastic modulus and strength of high strength Q690 deteriorated faster than those of mild steel.

2）With increases in the flange width-to-thickness ratio and the web height-to-thickness ratio， the ultimate bearing capacity of the member increases， but they have less effect on the ultimate bearing capacity of the members at elevated temperatures. The greater the temperature， the weaker the influence of other factors on the ultimate load-capacity， implying that the temperature of the member plays a leading role in affecting the ultimate bearing capacity of the members.

3）Whether the axial compressive steel members are loaded at an ambient or elevated temperature， the restraining effect of the flange on the web cannot be ignored and should be considered when estimating the web buckling stress.

4）Using the initial geometric imperfection of 0.1t （t is the plate thickness） or the initial geometric imperfection of b/100， the buckling stresses obtained by analysis are basically the same.

5）When the length of the element is relatively small， the element at high temperature is more likely to undergo local buckling， whereas， when the length is larger， the element at normal temperature is more likely to undergo local buckling

6）A simplified local buckling design method was proposed and recommended for designing the high strength steel section under axial compression. In addition， the current structural steel design codes were evaluated. It was found that GB 50017-2017 tends to provide a more safer estimate for the ultimate stress of the H-shaped section of the web than both EC3 and ANSI/AISC 360-10.

Acknowledgements

The authors would like to acknowledge the support from the National Program on Key Research and Development Project （Grant No.2016YFC0701203），and the Natural Science Foundation of China （Grant No.51878096）.References：

[1] ROMEIJN A. Steel-Concrete Bridges-III [M]. Faculty of Civil Engineering and Geosciences， Department Design and Construction-Section Structural and Building Engineering， 2006.

[2] SHI G， XU K L， LIN C C. Finite element analysis and design method study on the local buckling of 460 megapascal high strength steel I-section columns under axial compression [J]. Industrial Construction， 2016， 46（7）： 22-31.

[3] KNOBLOCH M， FONTANA M. Strain-based approach to local buckling of steel sections subjected to fire [J]. Journal of Constructional Steel Research， 2006， 62（1/2）： 44-67.

[4] WANG W Y， YANG X C， WANG B， et al. Design approach for local stability of axially compressed steel members at elevated temperature [J]. Journal of Chongqing University， 2015， 38（3）： 47-57.（in Chinese）

[5] CHIEW S P， ZHAO M S， LEE C K. Mechanical properties of heat-treated high strength steel under fire/post-fire conditions [J]. Journal of Constructional Steel Research， 2014， 98： 12-19.

[6] WANG Y B， LI G Q. Experimental and numerical study on the behavior of axially compressed high strength steel box-columns [J]. Engineering Structures， 2014， 58： 79-91.

[7] BAN H Y， SHI G， SHI Y J， et al. Overall buckling behavior of 460 MPa high strength steel columns： Experimental investigation and design method [J]. Journal of Constructional Steel Research， 2012， 74： 140-150.

[8] ZHOU F， TONG L W， CHEN Y Y. Experimental and numerical investigations of high strength steel weldedH-section columns [J]. International Journal of Steel Structures， 2013， 13（2）： 209-218.

[9] RASMUSSEN K J R， HANCOCK G J. Tests of high strength steel columns [J]. Journal of Constructional Steel Research， 1995， 34（1）： 27-52.

[10] BAN H Y， SHI G， SHI Y J， et al. Experimental investigation of the overall buckling behaviour of 960 MPa high strength steel columns [J]. Journal of Constructional Steel Research， 2013， 88： 256-266.

[11] SHI G， BAN H Y， BIJLAARD F S K. Tests and numerical study of ultra-high strength steel columns with end restraints [J]. Journal of Constructional Steel Research， 2012， 70： 236-247.

[12] WANG Y B， LI G Q， CHEN S W， et al. Experimental and numerical study on the behavior of axially compressed high strength steel columns with H-section [J]. Engineering Structures， 2012， 43： 149-159.

[13] LI G Q， LYU H B， ZHANG C. Post-fire mechanical properties of high strength Q690 structural steel [J]. Journal of Constructional Steel Research， 2017， 132： 108-116.

[14] KANG L， SUZUKI M， GE H B， et al. Experiment of ductile fracture performances of HSSS Q690 after a fire [J]. Journal of Constructional Steel Research， 2018， 146： 109-121.

[15] YUAN B. Local buckling of high strength steel W-shaped sections [D]. McMaster University， 2018.

[16] Code for Design of Steel Structures： GB 50017-2017 [S]. Beijing： China Architecture & Building Press， China Plan Press， 2017.

[17] Eurocode 3：Design of steel structures. Part 1.2： General rules-Structural fire design： EN 1993-1-2 [S]. Brussels： European Committee for Standardization （ECS）， 2005.

[18] Specifications for Structural Steel Buildings： ANSI/AISC 360-10 [S]. Chicago， 2010.

[19] Technical code for fire safety of steel structure in buildings： CECS 200：2006 [S]. Beijing： China Plan Press， 2006.

[20] Eurocode 3： Design of Steel Structures-Part 1-12： Additional Rules for the Extension of EN 1993 up to Steel Grades S700： European 1993-1-12 [S]. Brussels， 2007.

[21] LI T J， LI G Q， WANG Y B. Residual stress tests of welded Q690 high-strength steel box- and H-sections [J]. Journal of Constructional Steel Research， 2015， 115： 283-289.

[22] WANG W Y， WANG K， KODUR V， et al. Mechanical properties of high-strength Q690 steel at elevated temperature [J]. Journal of Materials in Civil Engineering， 2018， 30（5）： 04018062.

[23] LI G Q， ZHANG X J. Experimental studies of the material properties of SM41 steel at elevated temperatures [J]. Industrial Construction， 2001， 31： 57-59.

[24] TAN W. Experiments and research of steel material properties at elevated temperature [J]. Industrial Construction， 2010， 30： 61-63， 67.

[25] WANG W Y， KODUR V. Introduction[M]//Material Properties of Steel in Fire Conditions. Amsterdam： Elsevier， 2020： 1-27.

[26] ZHANG J. Study on residual stress and load capacity of welded high-strength Q690 steel column after fire exposure [D]. Chongqing： Chongqing University， 2019.

[27] WANG W Y， KODUR V， YANG X C， et al. Experimental study on local buckling of axially compressed steel stub columns at elevated temperatures [J]. Thin-Walled Structures， 2014， 82： 33-45.

[28] LI X， WANG W Y. Local bucking of Q690 high strength steel columns subjected to axial compression at elevated temperature [J]. Progress in steel building structures， 2020.

[29] BURGESS I W， OLAWALE A O， PLANK R J. Failure of steel columns in fire [J]. Fire Safety Journal， 1992， 18（2）： 183-201.

[30] Check & accept specification for steel structure work： GB 50205-2001 [S]. Beijing： China Plan Press， 2003.

[31] KAITILA O. Imperfection sensitivity analysis of lipped channel columns at high temperatures [J]. Journal of Constructional Steel Research， 2002， 58（3）： 333-351.

（編辑 章润红）