平行隧道开挖引起场地沉降的透明土模型试验研究

刘汉龙 钟海怡 顾鑫 向钰周 仉文岗

摘 要：為了便捷现代城市交通，地铁系统普遍采用平行隧道模式。平行隧道开挖引起的场地沉降预测一般基于单一隧道工况，利用简化叠加法生成变形剖面，而没有考虑两个隧道之间的相互作用。采用透明土模型试验技术，自主研发平行隧道模型试验装置及试验方法，研究了在砂质场地上开挖平行隧道引起的地表和地层沉降特性。通过模型试验探索了平行隧道间距、土体损失率、埋深等要素对地表和地表沉降的影响规律。在此基础上，量化了土体损失率和场地沉降值间的数值关系。此数值关系可为砂质场地中平行隧道施工与设计提供参考依据，也为隧道间距初选以及埋深的初步确定提供理论支撑。

关键词：透明土;平行隧道;模型试验;地表沉降;地层沉降

1 Introduction

With the rapid development of the modern city， burying the subway tunnels has proven to be an effective way to relieve traffic pressure on the ground. Accurate estimation of ground settlement is vital to ensure safety during the tunnel excavation. To this end， many early scholars have studied both the surface and the subsurface settlement for the excavation of the single tunnel[1-4]. However， single tunnel construction is rarely encountered in practice. Instead， parallel tunnels excavated sequentially are commonly constructed in urban subways to facilitate the movement of traffic in modern cities. In comparison to monitoring the deformation in clays[1-2]， the settlement caused by tunneling in granular soils （e.g.， sands and gravels） are more difficult and complex when considering key factors such as the relative density， which influences the shape and magnitude of the deformation[5]. Recently， the settlement of single tunnels in sand has been studied through model testing[6] and numerical simulation[7-8]. Yet the deformation induced by sequential excavation of parallel tunnels has not been fully revealed. Therefore， it may be a research hotspot in geotechnical engineering to investigate the deformation induced by the excavations of two parallel tunnels.

Many studies based on analytical deduction have been carried out to investigate the deformation induced by tunnel excavation， but they mainly aimed at the single tunnel[9-13]. Parallel-tunneling deformation prediction generally utilizes the simplified superposition method with the assumption the deformation arising from the excavation of the 2nd tunnel is unaffected by that of the 1st tunnel. However， previous research， particularly numerical studies that can fully consider the interaction between two tunnels， have indicated that this method may not be directly applicable to estimating the parallel tunneling-induced settlement in practice， since it may underestimate the resultant settlement， which may exert a negative effect on the safety of the nearby constructions[14]. The numerical simulation of tunneling which permits calculating internal soil deformation is widely used in the last decade[14-18]. However， not only is internal soil deformation difficult to validate against the actual measurements， but the key input parameters， which can directly and significantly impact the accuracy of the results， are quite difficult to obtain. Many scholars have focused on in-situ surface settlement induced by sequential excavation of parallel tunnels in a variety of soils. Since the in-situ test is costly and time-consuming， laboratory tests are widely used in performing two-dimensional trap door tests in dry sand[19] and lining installation in a centrifuge[20-21]. However， it is challenging to obtain the inner soil deformation and the failure pattern from the conventional model tests. Moreover， the results from traditional laboratory test are inevitably affected by the boundary conditions and the embedment of the rigid sensors has an effect on instrumentation accuracy due to the arching effect[22-23]. Recently the development of data-driven and soft computing methods， Zhang et al.[24-25] and Shahrour and Zhang[26] predicted the surface settlement induced by earth pressure balance shield tunneling， estimated the lining response for twin-tunnel construction， and performed TBM tunneling optimization. However， this kind of data-based method has an obvious deficiency in revealing the deformation characteristics in tunneling constructions， where the internal physical failure mechanism is often ignored.

To visualize the interioror the full-filed deformation， an advanced modeling technique using the transparent soil is adopted in this study， which was firstly developed by Allersma[27] and utilized by many scholars worldwide[28-29]， including in tunneling by Ahmed and Iskander[30-31]. And the intend of this paper is to explore the parallel-tunnel interaction and its influence on surface and subsurface settlements due to the second tunnel in sandy ground considering the spacing （S） between two tunnels， the magnitude of the volume of ground loss at the tunnel （Vl ）and burial depth （H and H0）.

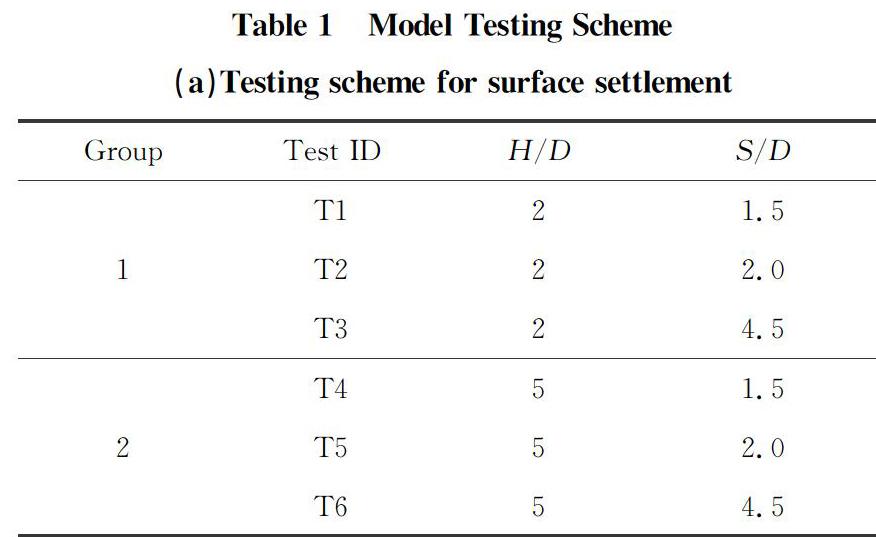
2 Experimental design

2.1 Testing apparatus

The model testing system was adopted to monitor the settlement variation during excavation. It consisted of a computer， an optical platform， a charge coupled device （CCD） camera， a disk laser， a plexiglass model tank， and processing software for particle image velocimetry （PIV） digital images. The optical platform was ferromagnetic stainless steel and the inner core structure on the top side offered considerable anti-disturbance capacity. The high resolution of the CCD camera was 1280×960 pixels， which could record the settlement during tunnel excavation continuously operated by the control program of the computer. The disk laser was EP532-3W along with 3 W output power， 532 nm wavelength， 10°-25° light angle and less than 1 mm thickness. The multifunctional model box made of acrylic plexiglass with each surface bonded by strong glue was capable of simulating the single tunnel test， parallel tunnels test and cross tunnels test， for a total of four tunnels （three on the front and one on the side）. Additionally， ribs were fixed at the bottom to restrain the deformation.

2.2 Testing materials

Fused silica sand， which has similar physical and mechanical properties to the proxy naturally graded sand， was adopted in this study to manufacture the transparent soil samples. The particles were 0.5-1.0 mm in size. The maximum dry density was 1.278 g/cm3， and the minimum was 0.907 g/cm3. The relative density was 55% and the internal friction angle was between 34° and 38°. The pore liquid was mixed with n-dodecane and the 15th mineral white oil with the mass ratio of 1：4 and its refractive index was 1.458 5. The periphery of the tunnel was isolated from the surrounding soil with a self-made film tube made of transparent and highly elastic thermoplastic polyurethane （TPU） film to prevent the pore liquid from flowing out along the tunnel model hole during the test. The drainage method was used to simulate the tunnel excavation process. One end of a rubber tube with a diameter of 50 mm was tied with a wire， and the other end was sleeved on a rubber plug with a drainage tube and tied with a rubber band to prevent potential water leakage. Before the test， the model box was cleaned， and the tunnel model， as well as the waterproof film tube， was set up.

3 Testing result and analysis

3.1 Surface settlement

3.1.1 Surface settlement due to excavation of the 1st tunnel

Fig.3 presents the measured surface settlement SV_A induced by TA under H （Depth from the surface to the tunnel axis level）/D=2.0 and 5.0， respectively. The normal probability Gaussian curves proposed by Peck[3] were used to fit the measured data. The surface settlement of the 1st tunnel excavation has good agreement with O'Reilly and New[2]， which is expected since TA is excavated in a greenfield site and this behavior is reected in the first tunnel settlement for all tests. Moreover， the Gaussian curves give a good fit when Vl=1.455% and 2.911%， then the goodness of the fit declines with the increase in Vl， which coincides with the observations by Marshall et al.[5].

As seen in Fig.4（a）， the maximum surface settlement Smax_Alinearly increases with Vl， which can also be seen in Shahin et al.[34]. From Fig.4（b）， the soil volume loss of surface settlement VS_A is smaller than Vl in all performed tests， especially at large Vl and H which is in good agreement with Zheng et al.[35]， who points out that the soil within the subsurface ground may exhibit an overall dilating response considering that the tests were conducted in a low-stress condition.

3.1.2 Surface settlement due to excavation of the 2nd tunnel

The resultant surface settlement SV of different groups is plotted inFig.5. Fundamentally， the distribution of the resultant ground settlement under H/D=2.0 and 5.0 changes from a “V” shape to a “W” shape step by step as S becomes larger.

From Fig.5， it is clear that the position corresponding to Smax_A is directly above TA during the tunnel excavation of TA. With the increase of Vl in TB， the position corresponding to Smax_B gradually moves towards the axis of TB and the asymmetry of the settlement trough becomes more significant in T1， T2， T3 and T4 （S=1.5D and 2.0D）. But for the tests （T3 and T6） that have larger S， the position corresponding to Smax_B is also just above TB， which means the excavation of TA has little influence on TB.

From Fig.6， it is clear that for T1， T2， T4 and T5， the corresponding location of the maximum surface settlement X moves toward TB as Vl increases and the asymmetry of the settlement trough also becomes more significant. For T3， the corresponding locations of the maximum surface settlement X remains constant and the excavation of TA has little impact on TB. For T4， although X does not change， the settlement trough curves appear as an inflection point at X=1.5D.

To further investigate the settlement caused by each excavation， the net surface settlement SV_B induced by TB is shown in Fig.7. The settlement of TB is obtained from the resultant ground settlement subtracting the 1st tunnel settlement. Gaussian curves are again used to fit the experimental data. The goodness-of-fit of the Gaussian curves is shown to decrease with the development of Vl in the TB excavation， which is similar to the observations in the TA excavation.

Fig.8（a） shows the Smax_B/D-Vl curves gained from the six tests. Basically， a non-linear relationship is found between Smax_B and Vl·Smax_B grows up gradually as Vl developed. Moreover， its magnitude is larger compared with Smax_A as plotted in Fig.3， which is consistent with the conclusion obtained in clayey soils that the larger settlement in the 2nd tunnel excavation is caused by the interaction between the two tunnels[36-37].

To further illustrate the impact of parallel-tunnel interaction on Smax_B， variations in Smax_B/ Smax_A with different Vl are plotted in Fig.8（b）. Basically， S appears to be the most dominant factor influencing the values of Smax_B/Smax_A. The influence of the twin-tunnel interaction is more significant in T1， T2， T4 and T5 （S=1.5D and 2.5D）， than in T3 and T6 （S=4.5D） as well as in the case of smaller H（H=2D）.

Fig.9 presents the values of the empirical coefficient for surface settlement k under different Vl for different H/D. Here， kl and kr represent the empirical coefficients of the left and right sides of the settlement trough， respectively. k gradually increases with Vl under the same S. Conversely， it decreases step by step with the increase of S. Moreover， kl gets closer to kr as S increases， indicating that both sides of the settlement trough tend to be symmetrical.

3.2 Subsurface settlement

The resultant subsurface settlement Su of different groups is plotted in Fig.10. Basically， the distribution of Group 1 gradually changes from a “W” shape to a “V” shape as H0（Depth from the subsurface to the tunnel axis level）/D becomes larger. And the distribution of Group 2 remains in the shape of a “W”.From Fig.11， it is clear that for Group 1， the corresponding location of the maximum subsurface settlement Xumoves toward TB as Vl increases. The asymmetry of the settlement trough for U1 and U2 becomes more significant， while for U3， the curves of the settlement trough undergo a process from asymmetry to symmetry and then back to asymmetry. As for Group 2， Xu is also just above TB and their settlement trough curves are quite similar， which means the excavation of TA has little influence on TB.

4 Summary and conclusions

Based upon the surface and subsurface settlements observed during the transparent soil model test， some useful conclusions are drawn as shown below：

1） With the increase of the ground volume loss， the Gaussian curve used to predict the ground settlement induced by the excavation of the two parallel tunnels demonstrates a decreasing trend.

2） The interaction of the parallel tunnels leads to greater maximum surface settlement Smax_B during the excavation of TB compared with that of TA. This effect weakens as the spacing between the parallel tunnels increases.

3） When S=1.5D and 2.0D， the excavation of the 1st tunnel has a significant effect on the surface settlement of the 2nd tunnel， and the corresponding location of Smax gradually moves towards the axis of the 2nd tunnel with the increase of Vl. Moreover， the asymmetry of the settlement trough becomes more obvious. When S=4.5D， the excavation of the 1st tunnel has a marginal influence on the deformation of the 2nd tunnel.

4） Under the same S， k gradually increases with the growth of Vl while it declines as S develops. The empirical coefficients k of the left and right sides get closer as S increases.

Acknowledgements

The authors would like to acknowledge the financial support from the Chongqing Construction Science and Technology Plan Project （No. 2019-0045）， Fundamental Research Funds for the Central Universities （No. 2019CDJDTM0007） and the Graduate Research and Innovation Foundation of Chongqing （Grant No. CYS18024）.

References：

[1] MAIR R J， TAYLOR R N， BRACEGIRDLE A. Subsurface settlement profiles above tunnels in clays [J].Geotechnique， 1993， 43（2）： 315-320.

[2] O'REILLY M P， NEW B M. Settlements above tunnels in the United Kingdom - Their magnitudes and prediction [C]//Proceedings of Tunnelling '82 Symposium， Springer， Berlin， 1982： 173-181.

[3] PECK R B. Deep excavations and tunneling in soft ground [C]//Proceedings of the Seventh International Conference on Soil Mechanics and Foundation Engineering， Mexico， Balkema， 1969， 3： 225-290.

[4] SCHMIDT B. Settlement and ground movement associated with tunneling in soils [D]. Urbana： University of Illinois， 1969.

[5] MARSHALL A M， FARRELL R P， KLAR A， et al. Tunnels in sands： the effect of size， depth and volume loss on greenfield displacements [J].Geotechnique， 2012， 62（5）： 385-399.

[6] FRANZA A， ZHOU B， MARSHALL A M. The effects of relative tunnel depth and volume loss on vertical settlements above tunnels in dense sands [C]//Fourth Geo-China International Conference. July 25-27， 2016， Shandong， China. Reston， VA， USA： American Society of Civil Engineers， 2016： 125-132.

[7] YANG B W， BLOODWORTH A. Numerical analysis oftunnelling in sand-A case study of a centrifuge test [C]//Proceedings of GeoShanghai 2018 International Conference： Tunnelling and Underground Construction， 2018.

[8] ZHOU B， ELKAYAM I， MARSHALL A. The effect of relative density on tunnelling-induced settlements - DEM simulations versus centrifuge test results[M]// Geomechanics from Micro to Macro. CRC Press， 2014： 589-594.

[9] BOBET A. Analytical solutions for shallow tunnels in saturated ground [J]. Journal of Engineering Mechanics， 2001， 127（12）： 1258-1266.

[10] CHI S Y， CHERN J C， LIN C C. Optimized back-analysis for tunneling-induced ground movement using equivalent ground loss model [J]. Tunnelling and Underground Space Technology， 2001， 16（3）： 159-165.

[11] CHOU W I， BOBET A. Predictions of ground deformations in shallow tunnels in clay [J].Tunnelling and Underground Space Technology， 2002， 17（1）： 3-19.

[12] PARK K H. Analytical solution for tunnelling-induced ground movement in clays [J]. Tunnelling and Underground Space Technology， 2005， 20（3）： 249-261.

[13] VERRUIJT A， BOOKER J R. Surface settlements due to deformation of a tunnel in an elastic half plane [J].Géotechnique， 1996， 46（4）： 753-756.

[14] ADDENBROOKE T， POTTS D M. Twin tunnel interaction： surface and subsurface effects [J]. International Journal of Geomechanics， 2001， 1（2）： 249-271.

[15] GONZLEZ N A， ROUAINIA M， ARROYO M， et al. Analysis of tunnel excavation in London Clay incorporating soil structure [J].Géotechnique， 2012， 62（12）： 1095-1109.

[16] KASPER T， MESCHKE G. A 3D finite element simulation model for TBM tunnelling in soft ground [J]. International Journal for Numerical and Analytical Methods in Geomechanics， 2004， 28（14）1441-1460.

[17] ZHANG W G， ZHANG R H， WU C Z， et al. State-of-the-art review of soft computing applications in underground excavations [J]. Geoscience Frontiers， 2020， 11（4）： 1095-1106.

[18] CHEN F Y， WANG L， ZHANG W G. Reliability assessment on stability of tunnelling perpendicularly beneath an existing tunnel considering spatial variabilities of rock mass properties [J]. Tunnelling and Underground Space Technology， 2019， 88： 276-289.

[19] VARDOULAKIS I， GRAF B， GUDEHUS G. Trap-door problem with dry sand：A statical approach based upon model test kinematics [J]. International Journal for Numerical and Analytical Methods in Geomechanics， 1981， 5（1）： 57-78.

[20] CHAPMAN D N， AHN S K， HUNT D V L， et al. The use of model tests to investigate the ground displacements associated with multiple tunnel construction in soil [J].Tunnelling and Underground Space Technology， 2006， 21（3/4）： 413.

[21] KIM S H. Interaction between closely spaced tunnels in clay [D]. Oxford， UK： Oxford University， 1996： 242.

[22] LEE C J， CHIANG K H， KUO C M. Ground movement and tunnel stability when tunneling in sandy ground [J]. Journal of the Chinese Institute of Engineers， 2004， 27（7）： 1021-1032.

[23] XIANG Y Z， LIU H L， ZHANG W G， et al. Application of transparent soil model test and DEM simulation in study of tunnel failure mechanism [J].Tunnelling and Underground Space Technology， 2018， 74： 178-184.

[24] ZHANG W G， LI H R， WU C Z， et al. Soft computing approach for prediction of surface settlement induced by earth pressure balance shield tunneling [J/OL]. Underground Space， 2020. https：//doi.org/10.1016/j.undsp.2019.12.003.

[25] ZHANG W G， LI Y Q， WU C Z， et al. Prediction of lining response for twin tunnels constructed in anisotropic clay using machine learning techniques [J/OL]. Underground Space， 2020. DOI：10.1016/j.undsp.2020.02.007.

[26] SHAHROUR I， ZHANG W G. Use of the soft computing techniques for TBM tunnelling optimization [J/OL]. Underground Space， 2020. https：//doi.org/10.1016/j.undsp.2019.12.001

[27] ALLERSMA H. Photo-elastic stress analysis and strains in simple shear[C]//Proc. Iutam Symposium on Deformation and Failure of Granular Materials， 1982： 345-353.

[28] CAI M， KAISER P K， MORIOKA H， et al. FLAC/PFC coupled numerical simulation of AE in large-scale underground excavations [J]. International Journal of Rock Mechanics and Mining Sciences， 2007， 44（4）： 550-564.

[29] NG C W W， SHI J W， HONG Y. Three-dimensional centrifuge modelling of basement excavation effects on an existing tunnel in dry sand [J]. Canadian Geotechnical Journal， 2013， 50（8）： 874-888.

[30] AHMED M， ISKANDER M. Evaluation of tunnel face stability by transparent soil models [J].Tunnelling and Underground Space Technology， 2012， 27（1）： 101-110.

[31] AHMED M， ISKANDER M. Analysis of tunneling-induced ground movements using transparent soil models [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2011， 137（5）： 525-535.

[32] LIU J Y. Visualizing 3-D internal soil deformation using laser speckle and transparent soil techniques [C]//GeoHunan International Conference 2009. August 3-6， 2009， Changsha， Hunan， China. Reston， VA， USA： American Society of Civil Engineers， 2009： 123-128.

[33] SADEK S， ISKANDER M， LIU J Y. Geotechnical properties of transparent silica [J]. Canadian Geotechnical Journal， 2002， 39（1）： 111-124.

[34] SHAHIN H M， NAKAI T R， ZHANG F， et al. Behavior of ground and response of existing foundation due to tunneling [J]. Soils and Foundations， 2011， 51（3）： 395-409.

[35] ZHENG G， TONG J B， ZHANG T Q， et al. Experimental study on surface settlements induced by sequential excavation of two parallel tunnels in drained granular soil [J].Tunnelling and Underground Space Technology， 2020， 98： 103347.

[36] CHAPMAN D， AHN S K， HUNT D V L. Investigating ground movements caused by the construction of multiple tunnels in soft ground using laboratory model tests [J]. Canadian Geotechnical Journal， 2007， 44（6）： 631-643.

[37] DIVALL S， GOODEY R J. Twin-tunnelling-induced ground movements in clay [J]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering， 2015， 168（3）： 247-256.

（編辑 胡英奎）