思维导图在数学德育教学中应用研究

张泉功

[摘 要] 本文详细分析了思维导图概念，指出思维导图是通过直观的图形将各种概念联系在一起，通过深层挖掘建立的一种发散思维图。思维导图突出特点为可视化、聚散性。思维导图的应用价值体现在：有助于培养学生的形象思维、思维导图培养学生系统化思想。详细研究了思维导图在数学德育教学中的应用，结果表明思维导图能帮学生构建数学知识结构、思维导图能帮学生加深数学知识理解、加强学生之间的互动效果。

[关键词] 思维导图;数学;德育

当前，数学教学中许多教师仍然采用传统的教学模式进行数学知识传授，其中讲授教学方式是普遍使用的方法。为提高数学知识教学质量，大量学者提出了先进的教学办法比如情境学习方法、思维导图等，其中思维导图具有形象、简单的特点被广泛应用到教学中。

一、思维導图的应用价值

1.思维导图概念

思维导图起源于20世纪60年代，由英国托尼·巴赞提出的一种笔记方法，该方法与传统的笔记方法截然不同。思维导图是通过直观的图形将各种概念联系在一起，通过深层挖掘建立的一种发散思维图，该过程中要记录思维的导向。思维导图提供了丰富的图形技术，通过图形导向可深度挖掘大脑潜力。这种技术非常适合知识与思维的导向，学生通过思维导图可直观地了解到知识架构，在知识理论学习中发挥了重要的作用。

2.思维导图的特点

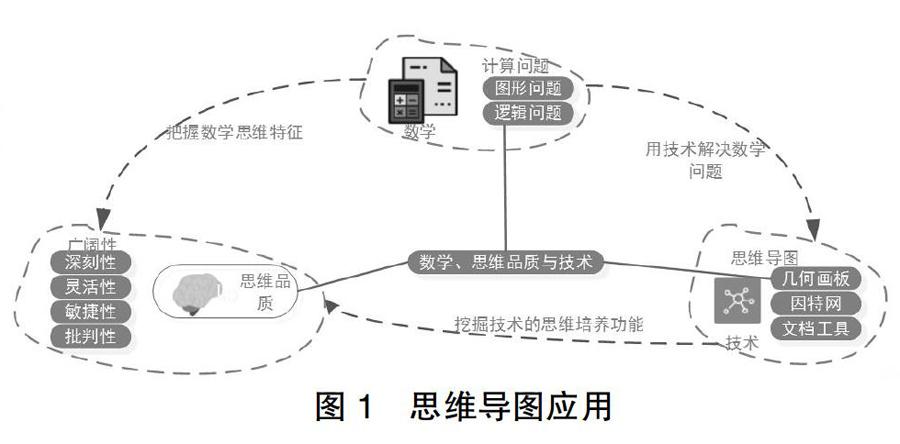
（1）可视化。该特点是指利用思维导向软件能把抽象的思维形象化，同时也可把隐含的信息显示出来，学生可根据自身的学习情况构建知识架构，从而提高学生的学习效率，这种技术已成为当前学生学习的重要手段。图1为使用思维导图构建的学生学习数学、思维以及技术的关系图。

（2）聚散性。思维导图采用视图方法将思维列出，展示出结果类似于数据结构中二叉树一分为二特点，同时又具有汇聚为一点的特点。教师在教学中可针对某一知识点利用思维导图让学生深入了解知识点所涉及的内容，这样学生即可把所学的知识点串联在一起，又可复习各个知识点。这样加深了学生对知识点的理解。

3.思维导图在数学教学课堂中的应用价值

2019年，教育部颁布了《教育部关于加强高中学业水平考试命题工作的意见》，该意见中指出了要提高命题质量、重基础知识、提高学生解决实际问题能力。目前，高中数学教学知识按照模块划分，导致知识点之间出现孤岛情况，学生在学习时无法将这些知识点组织在一起，造成学生很难深入理解数学知识点。这时就需要教师对教材知识进行提炼，思维导图正好具有将散点的知识组织在一起的作用。思维导图能够将人们的思维进行整理，通过图像方式展示，学生可通过导图更容易理解数学知识。通过归纳可知思维导图在数学教学课堂中的应用价值体现在如下两点。

（1）有助于培养学生形象思维。思维导图是将抽象的知识利用图像进行展示，这样有助于提高学生对知识的理解能力。研究表明，思维导图实际是对思维全过程的展示，采用图像方式有助于刺激人的左右大脑，最终达到激发人的左右脑协同功能，能够将枯燥的信息转变为便于记忆的图像信息，充分激发学生的记忆潜能。

（2）思维导图培养学生系统化思想。传统的数学教学方法存在教学知识点零散、逻辑不严谨、章节连接不紧密的缺点，导致学生学习数学知识时无法更深入地掌握课堂知识，隐含的知识无法显现出。而思维导图能够将数学知识点系统展示出来，学生通过观察导图更容易了解到知识点之间的关联。运用思维导图能够让学生加深对高中数学知识的记忆效果，其中思维导图中关键词选择会影响到学生记忆效果。因此，教师在讲解数学知识时应引导学生找到关键词，帮助学生构建思维导图，将高中数学知识串联在一起，能够提高学生的学习效率、节省了大量的学习时间。教师在复习高中人教版数学中的函数知识时可将初中的函数知识关联起来帮助学生绘制思维导图。教师绘制的思维导图从初中的函数概念、性质、表示方法等延伸到高中的导数等知识。函数的概念中可使用初中的一次函数，该过程学生印象深刻，将初中阶段的图像法应用到函数表示中，然后，不断引出分段函数，接着，引出函数的定义域、值域等问题。从函数的对称角度能够推导出函数的单调性、奇偶性等。从函数的可导性可引出函数的导数与积分概念。此外，该过程中可将知识拓展到高中物理知识直线运动，教师通过列举高中物理知识中直线运动的方程求导与数学上求导比较，结果表明结果一致，说明导数能够解决高中物理直线运动方程，这样，学生不再死记硬背高中物理公式，而是从数学角度进行高中物理知识的认知。教师可进一步将知识拓展，延伸到高中图像法解决高中物理难题。总之，思维导图能够加深学生对数学知识理解，并能将数学知识应用到物理知识中。

二、思维导图在数学德育教育中的应用

1.思维导图构建数学知识结构

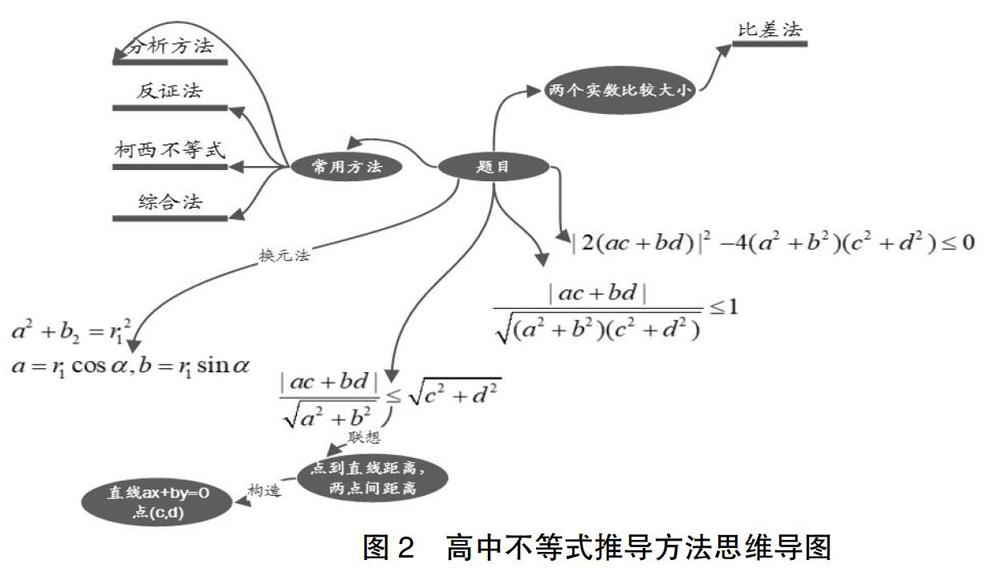
高中数学教师在进行高中数学课程讲解时可引导学生使用思维导图进行各个知识点的关联，学生建立自己的知识架构，将凌乱的知识组织在一起。中学生数学知识学习内容比较多，各个章节之间又独立涉及公式也多，如果使用传统的教学方式很难记住这些公式，如果采用思维导图则学生能够很快掌握课程章节结构。以高中不等式的推导方法为例。（见图2）

从不等式思维导图中可知高中不等式推导方法主要有反证法、柯西不等式、综合分析方法、换元法、比较法等。其中换元法是一种比较重要的方法，a2+b2+r12，a=r1cosa，b=r1sina，该方法能够简化不等式计算。而柯西不等式（a2+b2）（c2+d2）≥（ac+bd）2在不等式求解中也有重要作用。

高中数学知识点比较多，学生在解数学题时先准确审题，然后根据题找出关键的信息，然后利用各章节的思维导图将题关联起来。从不同的角度、知识点进行解决。使用思维导图能够让学生清晰了解数学中不等式管理，这样很容易掌握相应的计算方法，将零散的知识串联在一起。

2.思维导图加深数学知识理解

教师可向学生布置数学课程内容，采用思维导图进行绘制。学生使用思维导图绘制教学内容有助于对数学知识结构的整理。可让学生使用免费软件（GitMind）进行数学知识整理。学生使用该软件后加深了对数学知识系统的了解。通过本次实验，结果表明，使用思维导图软件后大多数学生能够根据自己对数学知识的理解绘制出个人思维导图。该过程能够培养学生的兴趣爱好、学生能正确地绘制思维导图从而获得成绩感，对学生的德育有促进作用。

3.加强学生之间的互动效果

数学知识是由大量抽象概念组成，课堂中使用思维导图后能够让学生之间相互交流、相互帮助，共同完成思维导图。这一过程中学生之间会有互动活动，比如有部分学生计算机操作熟练则进行思维导图绘制，部分学生知识架构清晰指导同学进行思维导图绘制。完成思维导图绘制工作后，可让大家一起进行交流。通过交流找出数学学习中存在的不足、解决方案。

传统数学教学模式一味讲解概念，导致学生在学习数学时存在枯燥情况，为解决这一问题，使用思维导图进行数学课程讲解，结果表明，思维导图的应用能让学生主动参与到教学中，这样教师与学生之间建立了互动关系、促进了情感交流，使课堂教学比较轻松愉悦;思维导图的应用让学生构建了自己数学知识结构，这样，学生可知道自身学习情况、教师也可了解到学生的学习状况。思维导图教学模式需要教师、学生有更高的素质，计算机水平、逻辑思维能力都需要加强提升。

参考文献：

[1]黄文功.中职教学中思维导图的应用探讨——以德育教学为例[J].广西教育，2020（18）：41-43.

[2]吴志丹.协作建构思维导图在数学复习课中的应用探究[J].电化教育研究，2010（07）：108-110.

[3]张丽萍，葛福鸿.运用思维导图工具培养数学思维品质的研究[J].教学与管理，2015（27）：106-108.

[4]李正成.例谈思维导图在解高中数学题中的应用[J].中学生数理化（学研版），2013（5）：35.

（责任编辑：朱福昌）