基于神经网络的山楂红酒香气成分色谱保留值的研究
2021-03-11秦正龙冯长君
秦正龙,冯长君
(1.江苏师范大学 化学与材料科学学院,江苏 徐州 221116;2.徐州工程学院 化学化工学院,江苏 徐州 221008)
山楂又称红果、仙果、山里果、山里红等,是蔷薇科山楂属植物山楂或山里果的成熟果实[1-2],在我国的云南、山东、贵州、东北、太行山南部及燕山山脉等地广泛种植[3],与北美、智利形成三大世界山楂种植中心[4],山楂资源十分丰富。但是,由于其口感酸涩,故鲜食量很少,而传统的加工品种也不多,仅有山楂酱、山楂糕、山楂罐头及山楂果脯等,产品附加值低[5-6]。果酒因其口感细腻、营养丰富、清亮透明、果香浓郁且酒精度低、节约粮食、保健价值高,是未来酿酒企业的发展方向。因此,以山楂为原料加工成果酒,既解决了山楂贮藏保鲜问题,又提升了附加值[7-8],促进区域经济发展。目前,对山楂果酒的研究主要集中在分离、鉴定、检测及工艺等方面[9-12],对其香气组分性质的研究则较少。神经网络是模拟人脑网络结构的一种信息功能处理系统,该方法结构简单、自适应及自学习能力强,可以构建高质的非线性模型,在药物、环境及食品等领域应用广泛[13-16],但利用神经网络方法研究山楂果酒香气成分鲜见报道。为此本研究采用神经网络方法中的误差逆传播多层前馈网络算法,建立香气成分色谱保留时间与其分子结构之间的神经网络模型并对其进行预测,为快速检测山楂果酒的风味成分,提高果酒品质提供一定依据。
1 材料与方法
1.1 材料与试剂
山楂红酒中48种香气成分的色谱保留时间(retention time,RT):取自参考文献[9]。
1.2 仪器与设备
Agilent 7890A-5975C气相色谱-质谱联用仪(gas chromatography-mass spectrometry,GC-MS):美国安捷伦公司;DH6000AH型电热恒温培养箱:天津市泰斯特仪器有限公司。
1.3 方法
1.3.1 分子结构表征
拓扑指数是对分子图的某种矩阵通过数学计算而获得的,是图的一种不变量,可揭示化合物分子的结构特征。只要拓扑指数蕴含了影响色谱保留时间的本质因素,那么,两者之间必然具有良好的相关性。
分子价连接性指数(mXtV)[17]定义成键的非氢原子i的特征值(δiv)为:

示和非氢原子i成键的氢原子数。
分子价连接性指数(mXtV)的计算公式为:

式中:m为指数的阶数;t为子图的类型,有链、星、环、星-链等4种子图,依次记作p、c、ch及pc。
电拓扑状态指数(Ei)[18]包含两个方面,一方面是原子的本征值,它是由每个非氢原子类型i的原子结构和拓扑环境共同决定,以“Hi”表示;另一方面是原子本征值的增量,它是由其他非氢原子扰动所产生的,以“ΔHi”表示。定义电拓扑状态指数(Ei)为:

式中:j为原子类型i的个数。
1.3.2 两类拓扑参数的计算
采用Chemoffice 2005绘图软件,画出文献[9]中山楂红酒48种挥发性香味化合物分子的结构图,然后在MATLAB软件中,使用张婷等[19]报道的方法编写计算程序,运算得分子价连接性指数(mXtV)及电拓扑状态指数(Ei)(见表1,限于篇幅,表中只列出了相关的6种)。

表1 山楂红酒香气成分的结构参数及色谱保留时间Table 1 Structural parameters and chromatographic retention time of aroma compounds in hawthorn red wine

续表
1.3.3 实验方法
将上述计算得到的山楂红酒中48种香气成分的两类指数用Minitab最佳变量子集回归,分析筛选与香气成分色谱保留时间相关性最优的变量集,并以Kubinyi函数(Kubinyi function,Kf)[20-21]作为判据,Kf值越大,模型的稳定性、预测能力就越强。
2 结果与分析
2.1 多元回归模型的确定
由表2可见,模型中随着变量数目的增多,R、R2和R2adj持续增大,S逐渐减小,但五元模型后,其数值变化均很小,且Kf在五元模型处出现最大值,说明该模型的质量最好。所以本实验选用4XpV、E12、1XpV、E1、0XpV为最佳变量组合。

表2 保留时间与mXtV、Ei的回归结果Table 2 Regression results of mXtV,nEiand retention time
将山楂红酒中48种挥发性香味化合物的色谱保留时间(RT)与上述优化筛选得到的5参数最佳变量组合4XpV、E12、1XpV、E1、0XpV进行多元线性回归,得到的模型为:

用模型(4)给出的预测值与实验值基本吻合(预测值1,见表1)。
2.2 模型(1)的质量检验
为了检验模型(4)的稳定性及预测能力,采用Jackknifed检验法进行检验,即每次从48个山楂红酒香气成分中剔除1个,用余下的47个组分建模,依次建立48个方程,得到48个相关系数,其平均值为0.979,与模型(4)的相关系数完全吻合。根据一般的统计标准,所建模型的R2>0.8,说明所建模型具有良好的预测能力。模型(4)的R2为0.958,另外,模型(4)的Kf最大,说明该模型的预测能力最好,稳定性最佳。为了进一步检验模型(4)的质量,将48个香气化合物分成两个集,即训练集和测试集。随机剔去序号为4、13、22、29和41共5个化合物,并作为测试集,剩余的43个化合物为训练集,按上述方法建立的模型为:
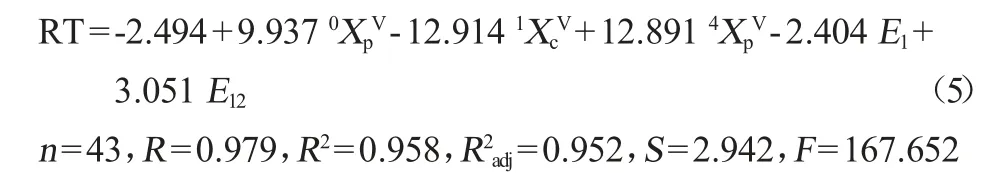
由模型(5)给出的序号为4、13、22、29、41五个化合物色谱保留时间的预测值分别为12.031、13.427、29.008、33.295、46.198,与模型(4)给出的预测值、实验值较好吻合,而且模型(5)和模型(4)十分相似:①两个模型中对应的各项,其数值非常接近;②两个模型的R、R2、R2adj、F、S等质量指标也十分接近。可见模型(4)是相关性、稳定性俱佳的模型。
为了判断模型是否存在离域点,将山楂红酒中48种挥发性香味化合物的Jackknifed相关系数作雷达图(图1),以0.970为圆心,间距为0.002,48个Jackknife 相关系数围绕原始模型(4)的相关系数(0.979)上下波动,且波动范围很小,Jackknife的相关系数全都处在0.977~0.982 之间,表明模型(4)没有异常的离域点。

图1 相关系数的雷达图Fig.1 Radar chart of correlation coefficients
2.3 建立神经网络模型
为了使模型的预测精准度进一步提高,使用误差反向传播方法的三层网络结构,以前述最好的多元回归模型中的5种分子结构参数作为神经网络的输入层单元,挥发性香味成分的色谱保留时间作为输出层单元,最佳隐蔽层的单元数按照许禄等[22]提出规则,经计算并优化得5。因此,网络结构为5∶5∶1。为了避免发生过拟合,把山楂红酒中48种挥发性香味物质划分为3个集,1组5个数据,其中的第1、3、4个数据即为训练集,其相关系数为0.997,每组的第2个、第5个数据则分别为测试集和验证集,它们的相关系数分别是0.999、0.999,总相关系数是0.998。由神经网络法得到的预测值见表1(预测值2),预测值与实验值颇为吻合,平均相对误差为3.31%。多元回归法与神经网络法实验值和预测值的关系见图2。由图2可知,神经网络法更优。

图2 两种方法预测值与计算值的关系Fig.2 Relationship between experimental and predicted values of the two methods
2.4 结果分析
在气相色谱分析中,影响色谱保留时间的因素很多,如果其他条件恒定下,那么色谱保留时间的长短决定于化合物分子和固定相之间的相互作用,相互之间的作用力越大,则色谱保留时间就越长。相互之间的作用力主要包含取向力、诱导力及色散力。分子价连接性指数把化合物结构图中各种子结构碎片进行加权计算,对于3个以上非氢原子组成的分子,即可产生链、簇、星和环等许多片段结构,能表征分子的大小、形状、分枝、表面积等,较好地揭示了色散力的强弱。电拓扑状态指数反映了化合物分子中成键原子的价态信息、固有特征、电子状态、拓扑环境及电性作用等,其数值大小较好地揭示了取向力、诱导力的强弱。因此,与神经网络方法结合,相关系数由原来的0.979提高到了0.998,预测能力大幅度提升。
3 结论
通过Minitab优化筛选的5 个分子结构参数与山楂红酒中48种香气成分色谱保留时间之间建立的定量构效关系模型,经检验不存在异常的离域值,具有良好的稳定性和较强的预测能力。神经网络法比多元回归分析法的预测准确度和纠错能力都更好,训练集的相关系数为0.997,测试集的相关系数是0.999,验证集的相关系数是0.999,总的相关系数为0.998,平均相对误差为3.31%,计算值与实验值很好吻合。
山楂果酒酸甜适口,酒体清爽优雅,不但有很高的营养价值,而且还有独特的保健及药理功能。近年来,人们的生活水平和质量不断提升,对天然食品的保健功能也更加重视。本研究结果为探索色谱分离条件,研究色谱保留机制提供有益的理论参考,对山楂果酒香气成分的结构表征、质量检验及药用价值的开发等,具有一定的实际意义。
