一种改进Logistic混沌序列安全网络编码设计

2021-03-11徐光宪崔俊杰

重庆邮电大学学报(自然科学版) 2021年1期

徐光宪，崔俊杰

(辽宁工程技术大学电子与信息工程学院，辽宁葫芦岛 125105)

0 引言

2000年，文献[1]发表的开创性论文标志着网络编码的诞生，他将网络中节点进行的编码称为网络编码，是指由输入到输出的任意因果映射，这是网络编码最广义的定义。网络编码的提出使得传统网络通信有了阶段性的突破。

关于网络编码的分类可分为随机线性网络[2]和确定性网络。网络编码的大量研究工作集中在随机线性网络编码，它为每一个信源过程维持一个系数向量，该系数向量是由每个编码节点进行更新。与其相反，在确定性网络中，每个编码节点之间是由固定链路组成的[3]，更适合用于稳定的组播通信网络中，其运算所需空间小、计算量小的优点使得组播通信效率得到提高[4]。文献[5]在2005年提出基于确定线性网络的数学编码，随着研究的深入，学者们更加注重于多源组播通信的研究[6]。为了降低多源组播问题的复杂度、使系统更稳定，文献[7]提出了虚拟信源的概念，该方案的计算过程十分繁琐，对网络系统的整体性要求较高。文献[8]在多媒体中应用了网络编码思想，利用分层组播的原理进行多媒体发送端与接收端的数据信息资源分配。本文也是针对多源组播通信网络来研究的，在已经运用组播路由算法确定好的网络拓扑结构的系统中，通过构造合适的网络编码算法来对网络编码方案进行构造。

在信息传输的过程中，攻击者对通信系统进行的攻击主要可以分为2种方式：即污染攻击和窃听攻击。传统网络编码的安全性可以基于信息论和密码学的2个层面来研究，香农[9]在信息论中指出：信息均可以二元数字化表示，即可以使用0，1比特作为经典信息的基本单元，提出了安全网络的完全保密定理，在该定理中为了防止窃听，发送端随机生成独立于信源的密钥，然后将密钥通过安全信道传输至信宿，确保信宿可以成功解码。

一般预防窃听的安全网络编码方案，窃听者旨在可以截取有限的数据包，所以在面对全局窃听攻击时,研究者最初提出在原始信源的地方加密整个消息传输的方法,但该方法给整个系统带来了很大的计算负担,编码效率不高。后来，有人提出对较短的编码向量在信源处进行加密，避免对较长的信息内容进行加密，将未加密的编码向量信息一起传输，辅助信宿节点进行解码，该方法虽然加密量小，但需要2轮解码操作，因此可能达不到预期的效率。文献[10]提出了一种典型的防窃听的安全加密方案，整个过程是对全局编码向量进行加密。徐光宪等[11]利用混沌序列来提高网络编码安全。然而，这些从信息论角度出发的安全算法，对全局窃听的攻击依然存在不足。文献[12]在已有的弱安全网络编码方案的基础上进行了一定的优化，该方案采用了密码学中序列密码的相关知识来防御攻击者的窃听，同时为信宿节点设置检错机制，在一定程度上抵抗了污染攻击的发生，但是并不能解决污染攻击带来的危害。本文对确定性网络中多源组播通信的传输效率和网络安全问题展开研究，利用逐层构造的方法构造编码节点的编码系数，从而使组播网络的带宽利用率得到提升，并使构造算法的收敛时间有所减少。此外，在编码构造方案的基础上提出了基于改进混沌序列的抗全局窃听和污染攻击的安全网络编码方案，增强了网络的安全性能。

1 确定性网络中逐层构造编码

1.1 理论依据

作为网络编码的2种主要构造算法，随机性编码更适合频繁发生动态变化的网络，而确定性编码则相反，在状态相对稳定的组播通信中更能体现优势。由于确定性网络的拓扑结构在周期内不会发生变化，所以在多源组播通信中需要做的就是在已经利用路由方案确定好拓扑结构的确定性网络中构造编码节点系数。

在确定线性网络中首先要构造编码节点的编码向量，然后再进行数据消息的传输。在通过相应路由算法得到网络拓扑结构的多源组播网络中，信源节点集合表示为S={S1,S2,…,Sn}，且信源处各个节点相互独立，信宿节点集合表示为T={T1,T2,…,Td}，因为此处讨论的是多源组播网络，所以集合中元素个数都大于1。利用最大流最小割定理就可以将minC(S,T)表示为信源端与信宿端的最小割值，那么，最小割值就等于信源端到信宿端的最大流maxflow(S,T)。当引入虚拟信源后，多源组播网络可以将多个信源端节点汇总成为一个信源节点，用S′表示，那么最小割最大流可以表示为

minC(S′,T)=maxflow(S′,T)

(1)

一个网络要进行数据信息的传递，首先要先确定这个网络的拓扑结构，具体实现方法是通过现有的组播路由方案来确定。在实际的信息传递过程中，网络拓扑发生动态变化后，会使路由方案也出现变动，变动后形成的网络拓扑中编码节点的编码系数可能不再适用于新的路由方案，这时就需要利用合适的办法来重新构造编码节点的编码系数，从而产生一个可行的编码构造方案。确定性编码可以通过调整部分编码节点的局部编码系数使网络节点接收到的全局编码矩阵满秩，从而保证信宿能顺利译码[13]。关于虚拟信源与实际信源的关系如图1。

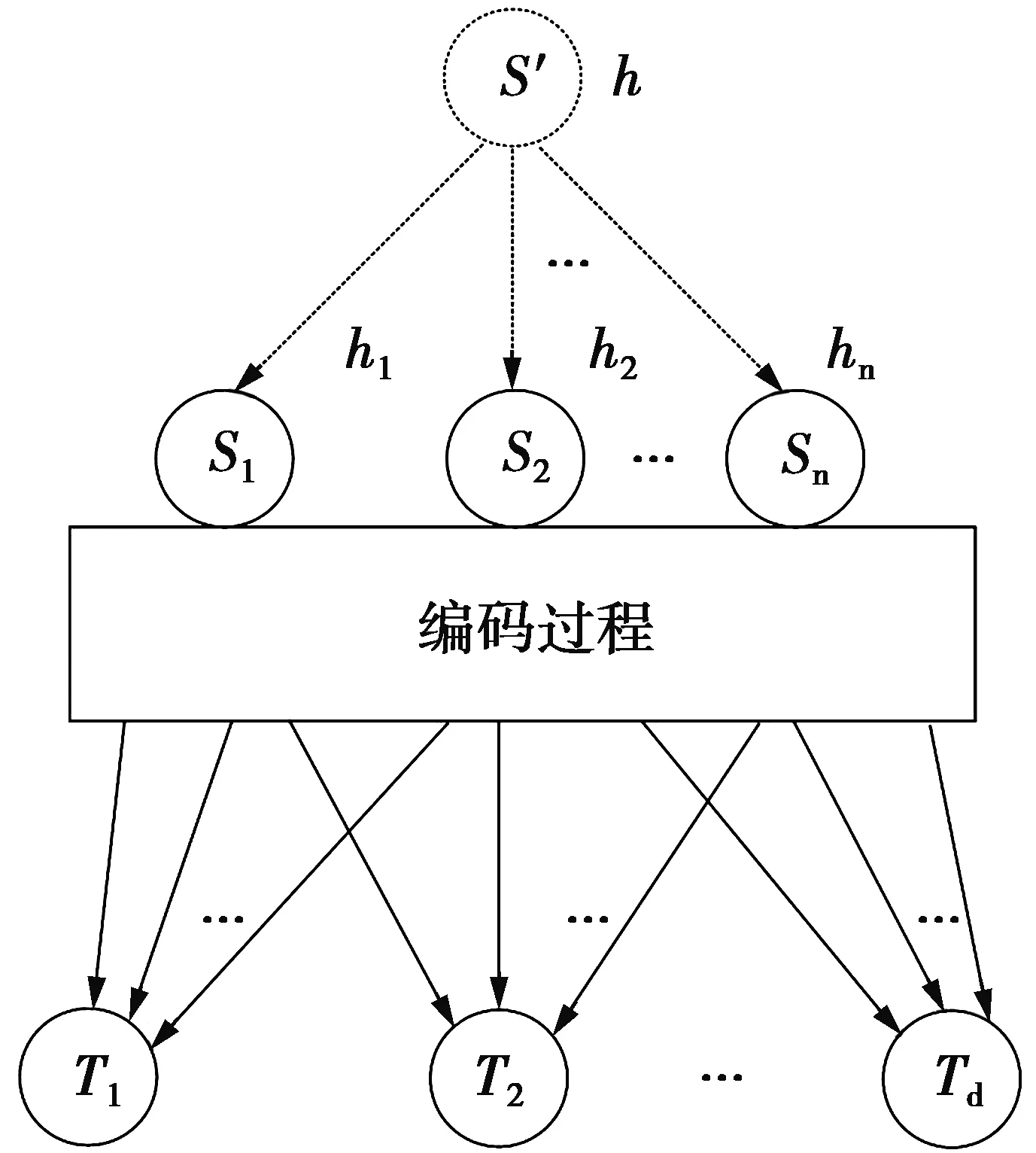
图1 虚拟信源示意图Fig.1 Schematic diagram of virtual source

1.2 基本原理

方案使用虚拟试播的方法来构造网络节点的编码系数，因为网络编码对网络节点的计算能力和储存空间有着比较高的要求[13]，所以本文采用了h阶的单位矩阵E作为试播矩阵。这样计算更便捷。那么，编码节点vij接收到的消息矩阵A就等于其所有输入链路全局编码向量构成的h×|ΓI(vij|阶矩阵为

A=E×[h×|ΓI(vij)|]

(2)

那么输出链路e上的信息向量y(e)等于其输入信息向量与编码节点vij新生成的全局编码矩阵之积为

y(e)=A×[h×|ΓI(vi)|]×(c1,c2,…,c|ΓI(vi)|)T

(3)

那么信宿端收到的编码信息矩阵就是其全局编码矩阵B。

设确定性多源组播网络拓扑中共有f层网络节点，不参与编码的源点集用f=1表示，即源点集是网络拓扑中的第1层节点，信宿节点是第f层节点。k代表某层编码节点的个数，vij表示第i层的第j个编码节点。其中，2≤i≤f,0≤j≤k。|ΓI(vij)|和|ΓO(vij)|分别表示编码节点vij的入度和出度。当p>0时就需要使用编码方案来构造节点vij的编码系数来得到可行的编码策略。

1.3 系统模型

本方案以一个4层网络拓扑模型来描述确定性逐层构造算法构造编码节点编码系数的过程，方案最终使信宿端的全局编码矩阵满秩，实现成功译码。在描述过程中，为了简明扼要地说明逐层构造算法的原理，令入度大于1的中间网络节点为编码节点，将其表示为vij；令虚拟试播矩阵为h×h阶的单位矩阵，用E来表示。图2是通过组播路由方案确定的网络拓扑结构，各个编码节点的初始局部编码系数为1，共4层网络节点，信源节点是3个，信宿节点是3个。由图2可知，当路由方案确定后，拓扑中可能会出现自然满足编码要求的编码方案。

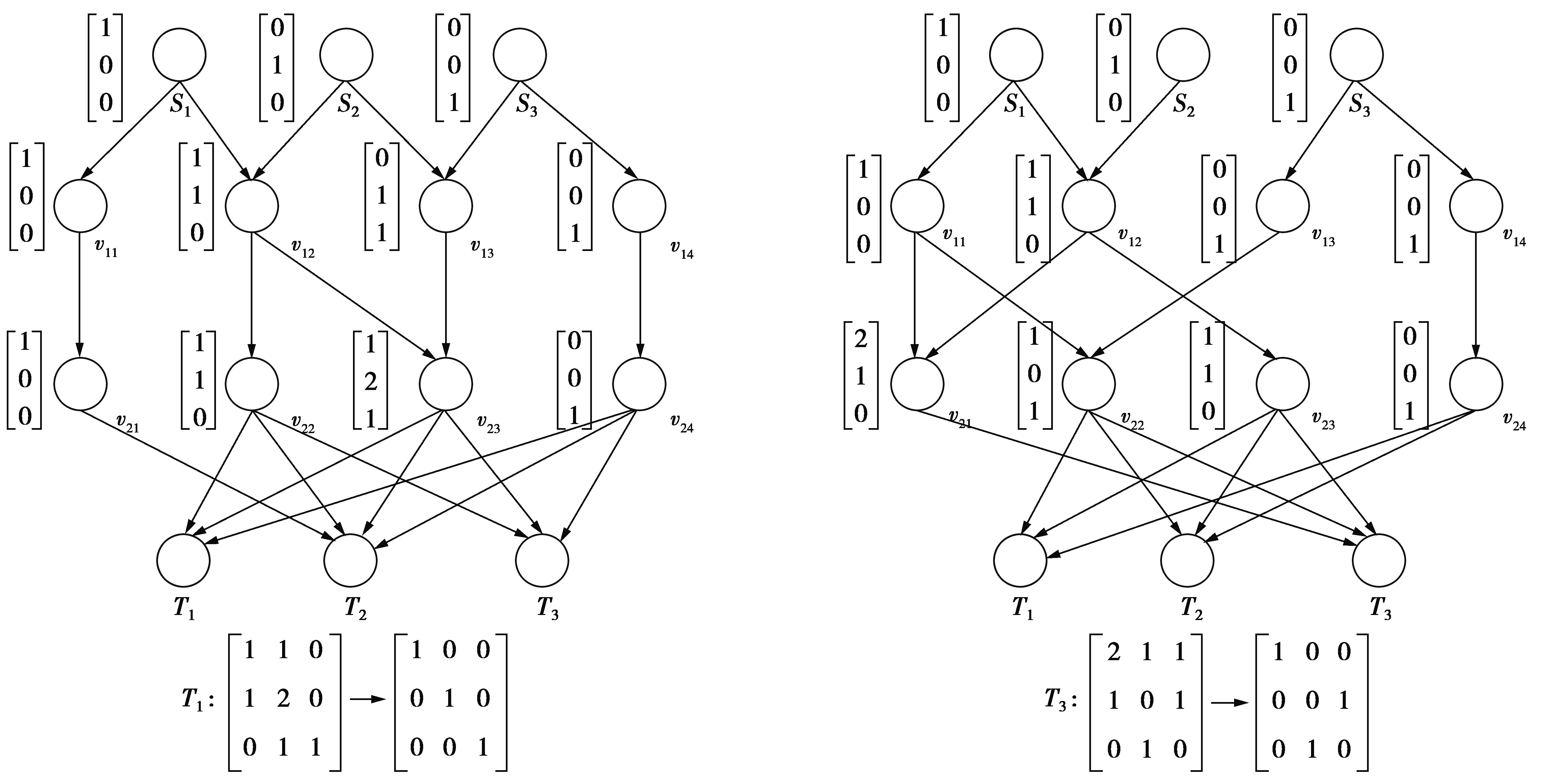
图2 自然满足编码要求的路由方案Fig.2 Natural routing scheme

从图2中可以看到，信源节点发送的试播矩阵是单位矩阵，各个编码节点的编码系数均默认为1，且3个信源的试播向量所构成的试播矩阵是满秩的，也就是说，信源节点处的全局编码矩阵是满秩的。然后，各个全局编码向量经过网络中间节点编码后传达至信宿，这时信宿节点接收到的各个输入链路的信息就是信源处全局编码向量经过编码后产生的新的全局编码向量。最后，每个信宿接收到的全部输入链路上的编码向量就构成了新的全局编码矩阵，这时需要判断的就是新的全局编码矩阵是否满秩，若满秩，就能保证信宿节点可以译码成功，否则，需要构造各个编码节点的编码系数。下面选择一个节点进行具体分析，以图2中最左边信宿节点T1为例，其对应的输入链路是编码节点v22，v23，v24的输出链路，3条链路的全局编码向量就构成了信宿节点T1的全局编码矩阵，通过初等行变换可得T1的全局编码矩阵的秩为3，即T1接收到的全局编码矩阵经过初等行变换后，显示的是满秩。同理，图2最右边网络拓扑的T3节点的全局编码矩阵也是满秩的。

在数据信息传输过程中还会出现一种数据冗余情况，本文算法对数据冗余链路进行修剪，从而提高带宽利用率，如图3。

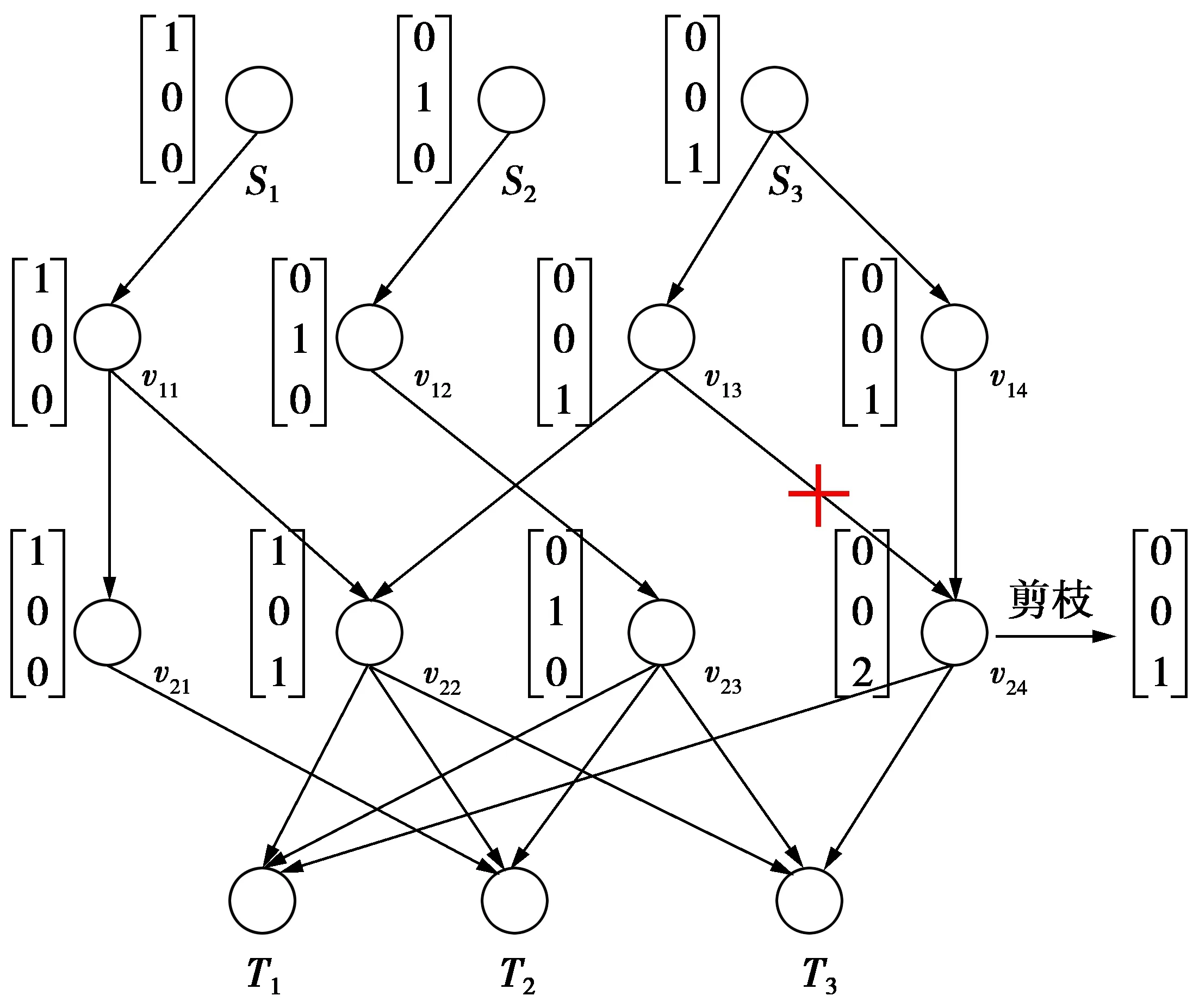
图3 剪枝处理示意图Fig.3 Schematic diagram of pruning branches

1.4 算法描述

本方案以一个4层网络拓扑模型来描述确定性逐层构造算法构造编码节点编码系数的过程，方案最终使信宿端的全局编码矩阵满秩，实现成功译码。图4中共有4个信源节点，4个信宿节点，虚拟信源S′不计入网络拓扑层数，所以一共有4层网络节点，即f=4。虚拟信源处的试播矩阵为4阶单位矩阵，即代表信源节点处的最初全局编码矩阵是满秩的。

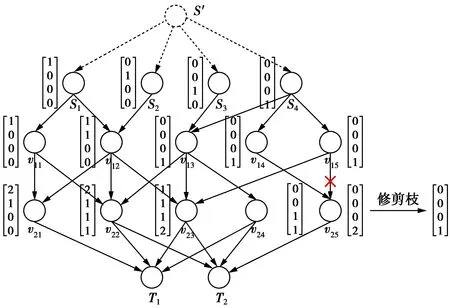
图4 算法原理示意图Fig.4 Schematic diagram of the algorithm

图中编码节点的全局编码矩阵是非满秩的，所以要对其进行修剪枝操作。修剪后，发现信宿节点T2的全局编码矩阵也是满秩的。

算法对整层p个编码节点执行上面的操作流程，直到该层节点全部获得满秩的编码矩阵，然后再进入下一层节点构造编码向量。整个算法的描述如下。

第1步初始设置；

第2步进行虚拟试播，中间网络节点执行编码操作，并产生全局编码向量，逐层转发逐层编码；

第3步统计第i层获得非满秩全局编码矩阵的编码节点vij的数目，记为p。若p=0，自动转跳下一层节点；若p>0，执行i-1层变换节点编码系数构造操作；

第4步ifp>0，标记与编码节点vij对应的第i-1层可变换节点位置，t=q；

ifq=|ΓI(vij)|-RMij，可变换节点全部作为变换节点；

eles ifq>|ΓI(vij)|-RMij，先进性优先级判断，再确定变换节点；

elseq<|ΓI(vij)|-RMij，执行修剪枝操作；

第5步构造变换节点局部编码系数，使编码节点vij的全局编码矩阵满秩；

第6步直到第i层的第p个编码节点完成构造编码系数的操作；Untilp=0;

第7步从上到下，逐层构造i+1→i；

第8步直到i=f；

第9步最终得到局部编码向量构造方案，算法结束。

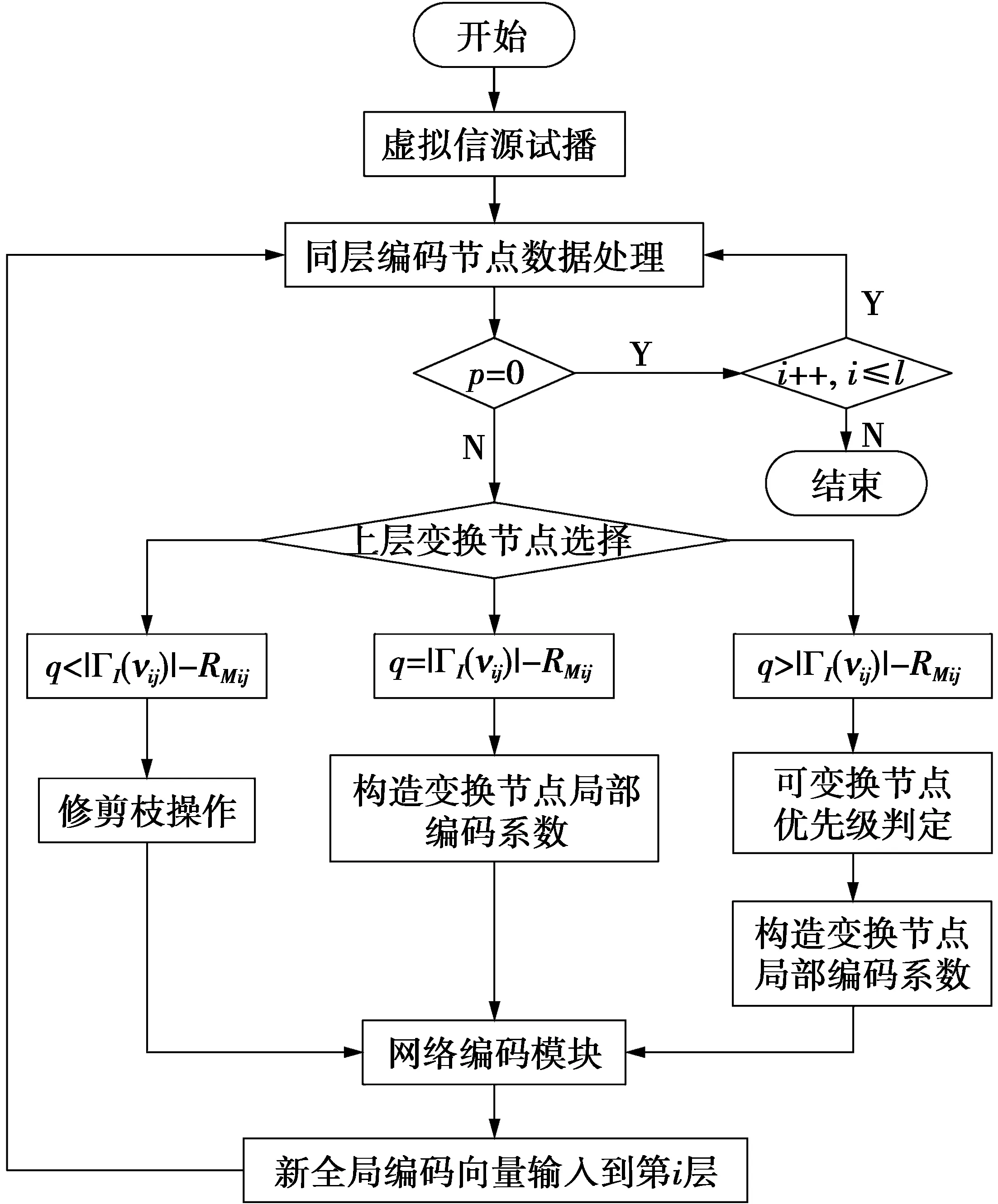
图5 算法示意图Fig.5 Schematic flow chart of algorithm

1.5 仿真分析

为了验证提出的确定性逐层构造算法的有效性和可行性，对算法进行了仿真，仿真实验的环境是Lenovo pc端，操作系统为Win8，使用了Matlab R2018、NS2-allinone2.26软件仿真结果如图6。

从图6可以看出，g不变时，当有限域达到一定大小后，构造方案的成功概率几乎为1，且保持不变。当g逐渐增大时，编码方案对有限域的需求范围也逐渐变大，但是不论g如何增大，只要有限域的范围大于一定取值，编码构造方案的成功率都近似为1。这是因为g增加表示编码节点增加，而编码节点选取编码系数后要保证信宿节点收到的全局编码矩阵满秩，构造方案才算成功，所以，需要选取的编码系数增加，所需的有限域也要变大。而当有限域范围满足编码系数选择的需求时，本确定性编码构造方案的成功率将保持在1附近。

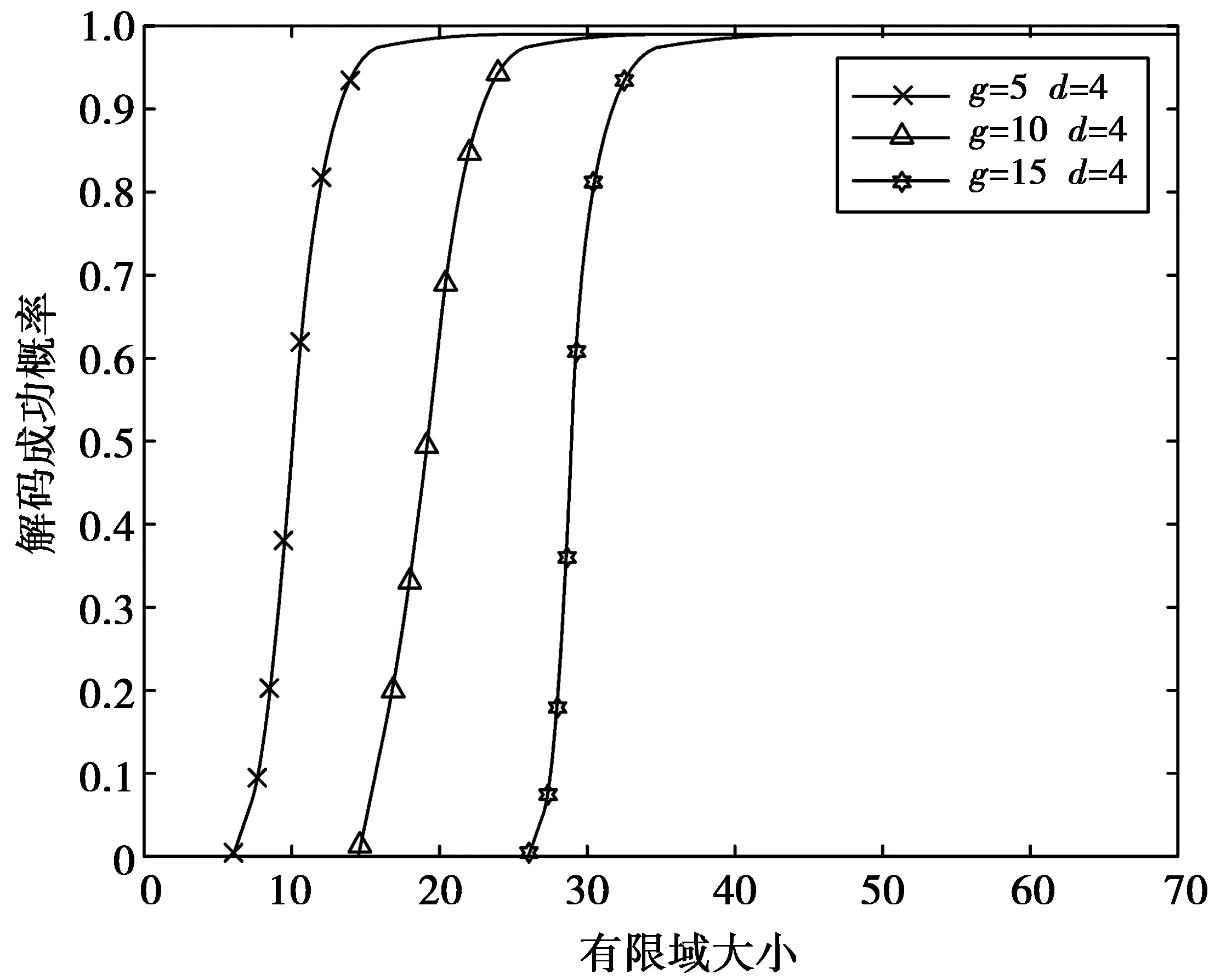
图6 g变化时方案成功的概率Fig.6 Success probability of the scheme with g change

2 安全网络编码设计

2.1 Logistic映射

Logistic映射是用来计算某类昆虫群体数量的一个模型，又叫作虫口模型[14]。众所周知，一类昆虫在繁衍时,其子代数量在不受其他恶劣因素影响的情况下是十分巨大的，昆虫子代的数量要远大于其亲代的数量，所以亲代数目在与子代数目相比时微乎其微，进而在统计群体总数时就可以将亲代数目忽略掉，那么该类昆虫群体数目就可以理解成是由单一世代的数目构成的。因此，有很多种类的昆虫其虫口数的增长是分步进行的，代与代之间没有累积计数。

令某类昆虫第n年内的群体总数为xn，第n+1年的群体数目为xn+1，因为n是非负整数，所以二者的函数关系可以用一个差分方程来描述为

xn+1=f(xn)

(4)

虫口模型初期最简单的表示方式为

xn+1=xn(a-bxn)

(5)

(5)式中：a表示昆虫种群的增长率；-bxn表示由于一些不可控因素造成的昆虫种群数目的饱和度。在某种特定情况下(可能是恶劣的环境抑或食物资源的短缺)某类昆虫群体密度较高，xn的数值极大时，必然会造成群体间的竞争。所以，为了在理论上更易于理解，便令a=b=μ来表示Logistic方程为

xn+1=μxn(1-xn)

(6)

xn之前表示的是某类昆虫第n年内的群体总数，但是在(6)式中，xn表示的是昆虫群体总数与特定环境下可以供养该类昆虫最大数目的比值。

通过分析，μ的取值不同会引起(6)式的取值有不同程度的变化，当x0=(μ-1)/μ时会使xn+1=xn，称此时x0的取值为不动点。但实际中xn的取值是有一定波动范围的，所以xn的取值应该随着μ的取值变化而变化。那么，当参数取值发生变化使得xn的取值由周期逐次加倍进入混沌状态的过程称为倍周期分岔通向混沌[15]。表1是μ取不同数值时，对函数关系式状态影响的分析。在动力学系统中，当0≤μ<3时，f(x)=μxn(1-xn)所决定的离散动力学系统形成的时间序列形态比较简单，产生的结果为不动点；当μ>3时，动力学系统就出现了分岔现象，在3≤μ≤4时，动力学系统先是表现出周期状态，随后产生的时间序列就通向了混沌状态，即由倍周期通向混沌状态；当μ>4时，整个动力学系统产生的时间序列的轨迹将更加复杂。

表1 Logistic混沌序列状态

2.2 改进Logistic映射

通过前面的分析，只有在μ=4时，所生成的Logistic混沌序列才在整个[0，1]上具有遍历性分布;而对于μ<4时，其所对应的分布区间均小于[0，1]。显然，这在实际的数字处理过程中，由于计算机本身的精度限制，会使得某些序列值之间容易产生聚集、重叠或交错的错误，不能达到期望的动力学特性，削弱了Logistic映射的系统性能，不利于实际的应用。

本方案采用了新的改进Logistic混沌序列，其在扩展系统参数μ的范围下所产生的混沌序列皆能一致地满足[0，1]的遍历性，并达到改善Logistic映射的系统性能的目的。改进后的Logistic混沌映射的数学表达式为

(7)

(7)式中：μ∈ ( 0，4]；n为迭代次数，n=0，1，2，… ；X0∈(0，1)。改进的Logistic混沌映射能一致地满足[0，1]的遍历性所对应的参数μ的取值范围，比传统的Logistic混沌映射的μ=4来说大了很多。测算结果表明，在μ∈(2.01，2.98)∪(3.11，4]时，改进的Logistic混沌映射所产生的混沌序列皆能一致地满足[0，1]的遍历性。

2.3 安全网络编码方案整体流程

2.3.1 编码方案整体流程

为提高网络安全性，本文将混沌序列应用于网络编码加密，在信源处加密最后一维数据，同时利用m序列扰动由另一密钥生成logistic混沌序列，在加密最后一维数据时将信源本身数据与混沌序列结合，提供序列反馈机制，将信源消息作为混沌序列扰动信号进行迭代，从而生成新的混沌数据，加密下一个信号，构造出一次一密的加密机制，增大了窃听者的破解难度。加密后的数据经过标准随机线性网络编码传递到信宿，完成解密过程，方案整体流程图如图7。

2.3.2 信源消息加密

在信源端加密的是原始数据信息，加密方式是当信源产生原始消息X=(x1,x2,…,xn)T之后，选取每个原始数据消息矩阵的最后一行元素进行加密，加密时采取的方法是引入改进Logistic混沌时间序列，网络中信源节点所要传输的消息记为X，X用矩阵表示是一个n×m阶的矩阵，代表一共包含n个长度为m的数据消息向量，即对(8)式中矩阵X中的xn实施加密处理，经过加密的xn表示为cn。

(8)

原始消息矩阵的最后一维数据加密的具体操作为：首先需要利用α作为初值生成Logistic混沌序列Y(α)，然后用混沌序列Y(α)对最后一维数据xn加密，加密过程为

cn=(xn1+Y(α),xn2+Y(xn1,α),…,

xnm+Y(xn1,xn2,…,xnm-1,α))

(9)

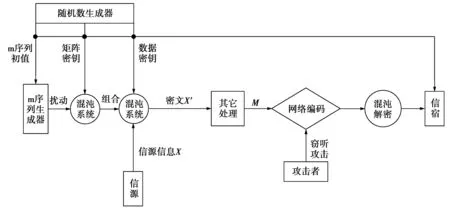
图7 编码方案整体流程图Fig.7 Overall flow chart of the coding scheme

那么加密后的原始消息就可以表示为X″=(x1,x2,…,xn-1,cn)T。

第1步加密后，接下来要进行的是构造信源节点处的全局编码矩阵。令全局编码矩阵为TX，安全方案的思路是从生成矩阵TX中对角线上的元素入手，通过m序列扰动Logistic混沌序列，将生成的序列执行取整操作来构造矩阵TX中对角线上的元素[16]。

(10)

当构造了全局编码矩阵TX之后，要进行的就是在信源节点处利用矩阵TX与已经加密了的信源消息X″进行线性构造，这样加密消息X′就诞生了

(11)

信宿端执行译码操作时需要知道全局编码向量，原始消息在信源处进行加密后，不会对中间的传输过程再进行任何多余的操作，也就是说信息在中间节点的传输是遵照其事先已经确定好的编码方式进行，本文是在确定线性构造方案的基础上进行信息传输的。在加密信息X′中加入单位矩阵，来标记中间节点进行编码操作时的全局编码矩阵。这样最终构成了信源节点需要发送的信息M′为

(12)

2.3.3 中间信道编码

中间节点编码过程实现的具体环境是在确定线性网络中，当网络拓扑发生变化后已经运用了确定性逐层构造方法重新构造了各个编码节点的编码向量。与此同时，整个中间编码过程所需的全局编码矩阵也是确定了的。因此，在确定线性网络中执行安全网络编码方案时，中间节点编码的编码系数矩阵是固定的，将会被矩阵M′里的单位矩阵进行记录，这里令利用逐层构造方案确定的全局编码矩阵为T2，M表示M′中除去前n列向量后信宿节点收到的编码信息矩阵，信宿节点接收的信息M可以表示为

M=T2X′

(13)

2.3.4 信宿端译码

在信源端加密时，已知信源信宿共享密钥。信宿节点首先通过接收到的消息恢复出X″，已知信源端的全局编码矩阵是通过密钥β、k和m序列初值m0构造出来的，所以当信宿端接收到n个线性无关的消息向量时，就可以利用高斯消去法恢复出X″，表示为

(14)

当恢复出X″后，对X″的最后一维消息cn进行解密，这样就得到了原始信源消息X，解码成功。

网络中一旦出现攻击者，问题就会变得非常复杂。攻击者能够潜藏在网络拓扑中的任何节点和链路处，攻击者除了采取搭线窃听的攻击方式来获取原始消息外，其目的还可以是阻止信源节点向信宿节点传递消息，扰乱正常消息的发送，或者至少通过一些攻击方式使信源节点传递到信宿节点的有用数据信息越来越少。那么以污染攻击为例，攻击者是具有十分强大的攻击能力的，而且攻击者对网络拓扑结构、网络编码方案都十分清晰，所以攻击者可以非法向网络中注入自己的信息，混淆到正确编码信息中，从而污染链路，实现污染攻击的目的。

在没有污染攻击出现时，信源端传送至信宿端的编码数据信息可以表示为M′。当污染攻击出现时攻击者会将污染信息注入到网络中，令污染信息矩阵为Z，Z是一个p0×m的矩阵，即矩阵Z代表p0个污染信息。这样一来，污染信息会与信源处发送的正确编码信息共同抵达信宿节点，这时接收端收到的最终信息矩阵用Y来表示，那么信宿节点就要通过接收到的矩阵Y来试图恢复出信源节点发送的原始数据信息。

首先需要明确的是矩阵Y是由编码信息M′和污染信息Z组成，可以表示为

Y=TXM′+T′Z

(15)

(16)

(15)—(16)式中：T表示的是信源消息传送至信宿节点经中间节点进行线性变换时的全局编码矩阵；T′表示的是对污染信息P执行线性运算操作时全局编码矩阵的信息。

由于正确的数据消息被污染，所以信宿节点是无法得到TX和T′的具体信息的，在这里信宿节点接收到的整个网络拓扑的全局编码矩阵用T″表示，信宿节点无法利用T″来直接恢复信源的原始数据消息。

提出一种构造线性列表的方法来帮助信宿节点区分污染信息和原始信息，最终使信宿能够剔除污染消息，正确进行译码。方案的核心思想是：信宿节点构造一个具有线性约束的关系式，而这个关系式只有信源处已经加密了的原始信息矩阵X′中的元素才能满足，即信宿端构造的线性列表的唯一解码必须是X′的相关信息才可以，因为攻击者在注入污染信息时，选择的都是随机数列，所以信宿端将收到的消息与列表进行比较，如果是污染信息就没办法满足列表的条件，这样污染信息就会被过滤掉，进而保证了信宿节点接收到的都是正确的编码信息。信宿节点接收到的矩阵Y是由污染消息和加密编码消息组成的，从Y中选取n+p0列线性无关的消息向量组成矩阵YS,由(16)式知道YS的秩不能大于n+p0，本文要求矩阵YS的秩为n+p0，矩阵YS是由Y的列向量张成的线性空间，YS一定要包含Y的前n列数据信息，Y的前n列对应于原始加密信息M′里的单位矩阵，而且YS的其余p0列是任意选取的，用M′S和ZS分别代表M′和Z对应于YS中的列，通过(16)式得

(17)

由于YS里任何一个向量都是线性无关的，而且是矩阵Y的最基础组成，可以利用一个矩阵F使得Y=YSF，这里的F可以由系数矩阵方程组求得。由于编码系数矩阵都是在伽罗华域上随机选取的，所以有很大的概率是可逆矩阵[17]，可得

M′=M′SF

(18)

Z=ZSF

(19)

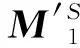
(20)

在进行鉴别之前还需要做一件事情，就是在信源处将原始信息X′写入列向量MX′，再构造一个矩阵D(矩阵D中元素选自于伽罗华域)，使得X′与D满足

DMX′=E

(21)

(21)式中，矩阵D是公开的，且D唯一。当信宿节点接收到最终消息Y时，就能够计算出矩阵F，并且信宿端知道矩阵D的信息，这样利用(20)式即可得到一个消息M′，至于该消息是否真的属于原始信息，通过(21)式即可鉴别，这样信宿端就可以对污染的信息进行筛选，保留下来的都是经过编码后的正确信息，从而该安全方案在一定程度上抵制了污染攻击的发生，最终信源端节点再利用没有污染攻击时的解码方案进行解码[18]。

2.4 加密仿真图

为了验证安全网络编码[19]方案的有效性，本文分别对文本和图片进行了加密解密仿真操作，利用Matlab对本文的加密方案进行实现。仿真时，首先利用本文安全网络编码方案对文件进行加密处理，然后再对加密后的文件进行解密操作，正确的加密操作是利用密钥进行解密，最后模仿窃听者，在不知道全部密钥的情况下试图对文件进行解密操作。这些操作的结果经过仿真都会逐一呈现出来仿真结果如图8、图9。

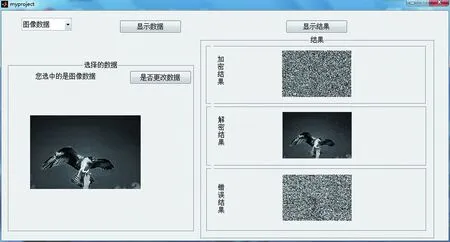
图8 加密解密仿真结果1Fig.8 Simulation results 1 of enciyption and decryption

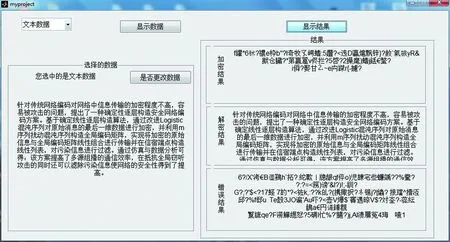
图9 加密解密仿真结果2Fig.9 Simulation results 2 of enciyption and decryption

3 对比分析

3.1 安全性对比

文献[10]提出的算法是最典型的初级抗全能窃听安全网络编码方案，只能抵御初级全能窃听；文献[11]中的方案在实现抵抗全能窃听的同时还能实现防污染攻击，在抵抗污染攻击时采用了检错码，为信宿节点设置检错机制，对接收到的编码信息进行检错，但是无法进行改错，也就是说只能发现污染攻击，但是无法追溯到污染源来改正错误，所以只是在一定程度上抵抗了污染攻击的发生。文献[12]的算法也只是达到了防全能窃听的效果。方案对比如表2。

表2 各方案性能对比

表2中的加密工作量为加密信息的数量，其中文献[10]提出的算法是对信源处的全部编码系数进行加密，所以加密工作量为m2；文献[11]中的算法是利用密码序列对信源处的原始消息进行加密，所以加密工作量为mn；文献[12]中的算法既对原始信源消息进行了加密，又对全局编码矩阵进行了加密，所以加密工作量为mn+m2；本文提出的算法需要对信源处的编码系数矩阵的对角线元素和原始信息最后一维数据进行加密，所以加密量为m+n。相比之下，本文的加密量更少一些，有助于提高编码效率。

3.2 编码时间对比

在比较时各个方案对等长数据进行编码，然后观察各个方案所需加密编码的时间。用Matlab进行仿真时，令编码长度为n=1 500，网络组播容量为8，伽罗华域的大小设为GF(q)=256，信息包数小于5 000个，仿真结果如图10。

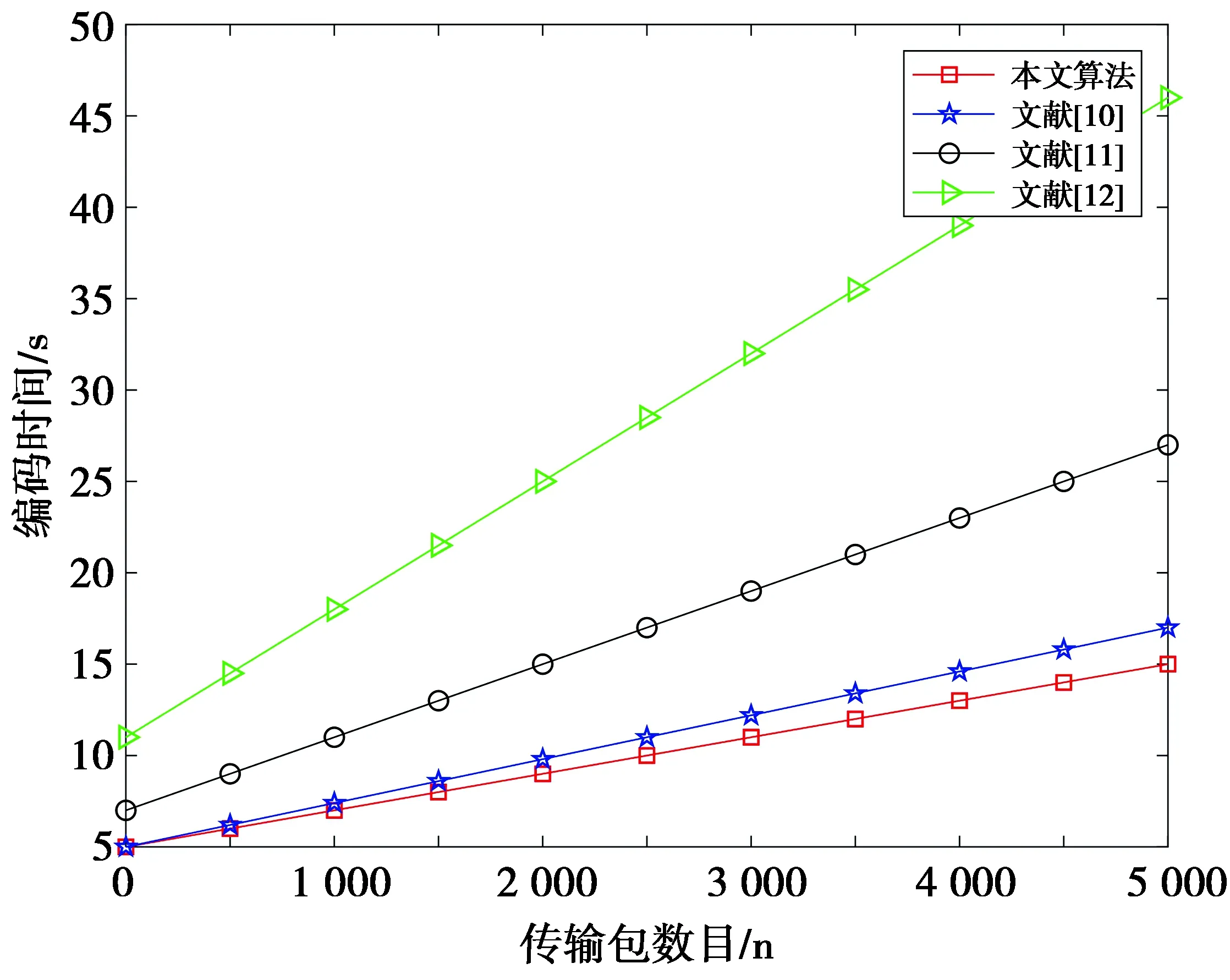
图10 各方案编码时间比较Fig.10 Comparison of coding time of each scheme

从图10中可以看出，文献[10]提出的算法采用的是高级加密标准，所以即便该方案与本文方案一样是加密消息矩阵的后一维数据，但是相比至下，本文的编码效率更胜一筹；文献[11]是典型的采用置换方式加密的方案，其加密的方法非常典型，但是由于置换时，会耗费一部分时间，同时该方案既对原始信息进行了加密处理，又对全局编码矩阵进行了加密处理，庞大的加密量使算法的加密时间过于冗长。同时该方案只能防止窃听攻击的发生，无法抵抗污染攻击的威胁；文献[12]中的算法运用密码流的方式来加密信息，其加密时所用的编码时间相对来说是适中的，而之所以会比本文算法时间略多一些，是因为该方案的带宽利用效率低了一些，同时与本文相比算法复杂度略高。与本文方案一样，该方案既能防止全局窃听，还能在一定程度上抵御污染攻击的发生。

3.3 额外开销对比

随着网络规模的增大，各算法的开销也迅速增加，从带宽开销和算法复杂度进行对比，如表3。

表3 各方案参数对比

文献[10]编码方案中，由于网络中需要将加密的编码系数放到数据包中进行传输，因此发送的数据中每一行都增加m个符号；类似地，文献[11]需要将预编码矩阵中的非零元素作为数据发送至信道中，带宽开销为r+1；文献[12]中的方案发送的数据中每一行都增加n个符号；本文算法也没有在数据中加入额外编码向量，没有额外占用带宽。

文献[10]编码方案的计算复杂度为O(m2n)；文献[12]采用的是稀疏的编码矩阵组合信源消息，相对而言降低了编码的复杂度，复杂度为O(mn)；文献[11]中采用矩阵的加密复杂度和编码参数r有关，编码复杂度为O(rmn)；本文采用的加密方式也是稀疏矩阵，加密复杂度为O(mn)。

4 结论

在确定性逐层构造算法上，从密码学的角度出发，提出了一种安全编码方案，方案利用改进混沌序列只对原始数据消息的最后一维数据进行加密，同时利用m序列扰动混沌序列生成的全局编码矩阵，并将编码矩阵与加密消息线性组合后进行传输，最后信宿端节点构造线性列表对污染信息进行过滤。实验表明，网络经加密后安全性能得到提升，在抵抗全局窃听的同时还可以滤除污染信息，提高了网络传输效率。