过渡金属原子掺杂的锯齿型磷烯纳米带的磁电子学特性*

张华林 何鑫 张振华

(长沙理工大学物理与电子科学学院, 长沙 410114)

利用基于密度泛函理论的第一性原理方法, 研究了掺杂铁、钴和镍原子的锯齿型磷烯纳米带(ZPNR)的磁电子学特性.研究表明, 掺杂和未掺杂ZPNR 的结构都是稳定的.当处于非磁态时, 未掺杂和掺杂钴原子的ZPNR 为半导体, 而掺杂铁或者镍原子的ZPNR 为金属.自旋极化计算表明, 未掺杂和掺杂钴原子的ZPNR 无磁性, 而掺杂铁或者镍原子的ZPNR 有磁性, 但只能表现出铁磁性.处于铁磁态时, 掺杂铁原子的ZPNR 为磁性半导体, 而掺杂镍原子的ZPNR 为磁性半金属.掺杂铁或者镍原子的ZPNR 的磁性主要由杂质原子贡献, 产生磁性的原因则是在ZPNR 中存在未配对电子.掺杂位置对ZPNR 的磁电子学特性有一定的影响.该研究对于发展基于磷烯纳米带的纳米电子器件具有重要意义.

1 引 言

最近, 实验上通过机械剥落方法从块体黑磷分离出来一种新的二维材料—磷烯[1,2], 立即受到普遍关注.研究者从施加应力[3−6]、引入缺陷[7,8]、表面吸附[8−10]和取代掺杂[10−15]等几个角度出发,对磷烯进行了广泛地研究.结果表明, 磷烯具有优越的电子特性, 在未来纳米电子学中具有广阔的应用前景[16−19].通过裁剪二维磷烯, 可以获得准一维的磷烯纳米带(PNR).根据边缘结构不同, PNR分为锯齿型磷烯纳米带(ZPNR)和扶手椅型磷烯纳米带(APNR).裸边ZPNR 为金属, 且与纳米带的宽度无关; 而裸边APNR 为间接带隙半导体, 其带隙随纳米带宽度的增加而减少[20−22].边缘氢饱和后, ZPNR 转变为近直接带隙的半导体, APNR转变为直接带隙半导体.边缘用氢饱和后的ZPNR和APNR 的带隙随着宽度的增加而减小[20−24].边缘被F, Cl, O, S, Se, Fe, Co, Ni 和 OH 等不同原子或基团饱和的PNR 的电子特性也被广泛研究[25−28].此外, 如Guo 等[29]发现在边缘氢饱和的APNR中央或边缘掺杂C 原子, APNR 转变为金属.Zhou等[30]发现在裸边APNR 的中央或边缘掺杂B, N, F 和Al 原子, APNR 仍然是半导体, 而在裸边APNR 的中央掺杂C, O, Si, S 原子, APNR 转变为金属.

目前对磷烯纳米带磁性的研究也有一些报道,例如, Du 等[31]研究了裸边ZPNR 在4 种磁构型下的磁性, 这4 种磁构型分别为: 铁磁(FM)αα−αα、反铁磁(AFM−1)αα−ββ、反铁磁(AFM−2)αβ−αβ、反铁磁(AFM−3)αβ−αβ, 研究表明裸边ZPNR的FM 态和AFM−1 态无磁性, 而AFM−2 态有磁性.Zhu 等[32]发现边缘氢饱和的ZPNR没有磁性.Ding 等[33]发现OHO 和 OH 钝化的ZPNR 和APNR 具有磁性.Ren 等[34]发现边缘用OH/NO2(或NH2/NO2)与O 按2∶1 比率的饱和ZPNR 可实现自旋极化半金属.Zhou 等[30]发现在裸边APNR 的边缘掺杂C, O, Si 和S 原子, APNR有磁性.然而对磷烯纳米带如何获得半金属, 如何诱发高性能的磁性, 以及诱发磁性的机理等仍需进一步研究.

本文采用基于密度泛函理论(DFT)的第一性原理, 探讨掺杂过渡金属铁(Fe)、钴(Co)和镍(Ni)原子的ZPNR 的磁电子学特性, 以及掺杂位置对其影响.研究表明, 在ZPNR 中掺杂不同的杂质表现出不同的特性, 有的有磁性, 有的没有磁性,提出了在ZPNR 中实现半金属的一种新方法, 并且掺杂位置对ZPNR 的磁电子学特性有一定的影响.这些研究结果对于发展基于磷烯的纳米电子器件具有重要意义.

2 计算模型和方法

掺杂ZPNR 的几何结构如图1 所示, 其中图1(a)和图1(b)分别为俯视和侧视图.图中模型结构为计算选取的超原胞, 纳米带沿图1(a)中Z 方向延展.图中白色、橙色和绿色小球分别表示H, P 和Ni 原子, n 表示ZPNR 的带宽, 即沿宽度方向的锯齿型磷原子链的排数, 图中ZPNR 的带宽n = 8.图中的x 表示掺杂的位置, 分别用Fe,Co 和Ni 取代x 位置的P 原子.作为例子, 图1(a)和图1(b)中的x 位置为Ni 原子.为了叙述方便,将Fe, Co 和Ni 原子取代P 原子后的ZPNR 分别称为Fe−ZPNR, Co−ZPNR 和Ni−ZPNR.为了消除悬挂键, 所有ZPNR 边缘用H 原子饱和.

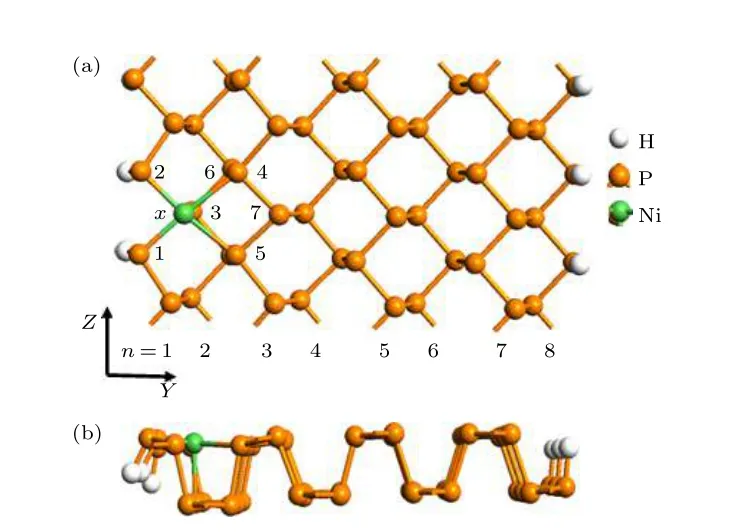
图1 掺杂ZPNR 的模型结构Fig.1.The geometric structure of doped ZPNRs.

采用基于密度泛函理论(DFT)的第一性原理的ATK(Atomistix ToolKit)软件包对几何结构进行优化和计算电磁性质, 目前这个软件包已被广泛用于纳米结构的研究中[35−38].模型结构在非磁状态下进行优化.结构优化收敛的标准是作用在每个原子上的力小于0.01 eV/Å.为了求解Kohn−Sham方程, 交换关联势采用广义梯度近似(GGA)中的PBE 近似, 赝势采用模守恒赝势, 基函数组选用DZP (double ζ +polarized).在 简 约 布 里 渊 区 的k 点抽样采用1 × 1 × 30.能量截断半径(mesh cut−off)采用75 Hartree.非周期方向, 即超原胞的X 和Y 方向的真空层设置为20 Å.

3 计算结果与讨论

3.1 结构和稳定性分析

为了便于说明掺杂ZPNR 的结构, 在图1(a)中对杂质原子附近的P 原子进行了编号, 分别为1—7.相应的P 原子用Pi表示, 其中i = 1, 2, 3,4, 5, 6, 7.由图1 可见, 取代掺杂后, 杂质原子附近的ZPNR 结构发生了一些形变, 最明显的变化就是杂质原子与周边5 个P 原子(P1—P5)成键, 而原始ZPNR 的P 原子只与相邻3 个P 原子成键.杂质原子与周边5 个P 原子之间的键长如表1 所示, 表中d1—d5分别为杂质原子与其邻近的5 个磷原子P1—P5的键长.作为对比, 表中还列出了未掺杂ZPNR 的相关参数.由表1 可见, 未掺杂ZPNR 的d1, d2和d3相等, 都为2.25 Å, 与以前的计算结果一致[11−13].掺杂ZPNR 的键长与未掺杂ZPNR 的键长相比略有增减, 但相差不大, 其中Ni−ZPNR 的d4和d5增加幅度最大, 大约增加了10%, 而其余键长的增减幅度不足4%.掺杂后, 杂质原子与P4, P5原子成键, 结果导致杂质原子略微向纳米带对称中心移动.

为了研究取代掺杂结构的能量稳定性, 分别取各掺杂ZPNR 的超原胞计算结合能Eb, 其定义为[39−41]

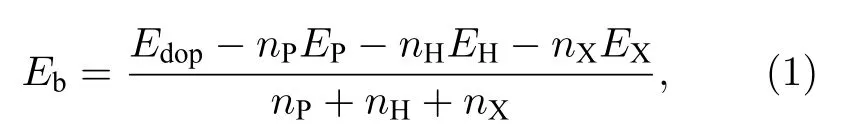
其中Edop为掺杂ZPNR 超原胞的总能量; EP,EH和EX分别为单个P、H 和杂质原子的能量, nP,nH和nX分别为超原胞内P, H 和杂质原子的数量, 其中杂质原子分别为Fe, Co 和Ni.计算结果如表1 所示, 表中还列出了未掺杂ZPNR 的结合能.由表1 可见, 各掺杂和未掺杂ZPNR 的结合能都为负值, 说明各掺杂和未掺杂ZPNR 的结构都是稳定的.

表1 掺杂和未掺杂ZPNR 的键长、结合能和总能差Table 1.The bond lengths, binding energy, and total energy difference of doped and pristine ZPNRs.

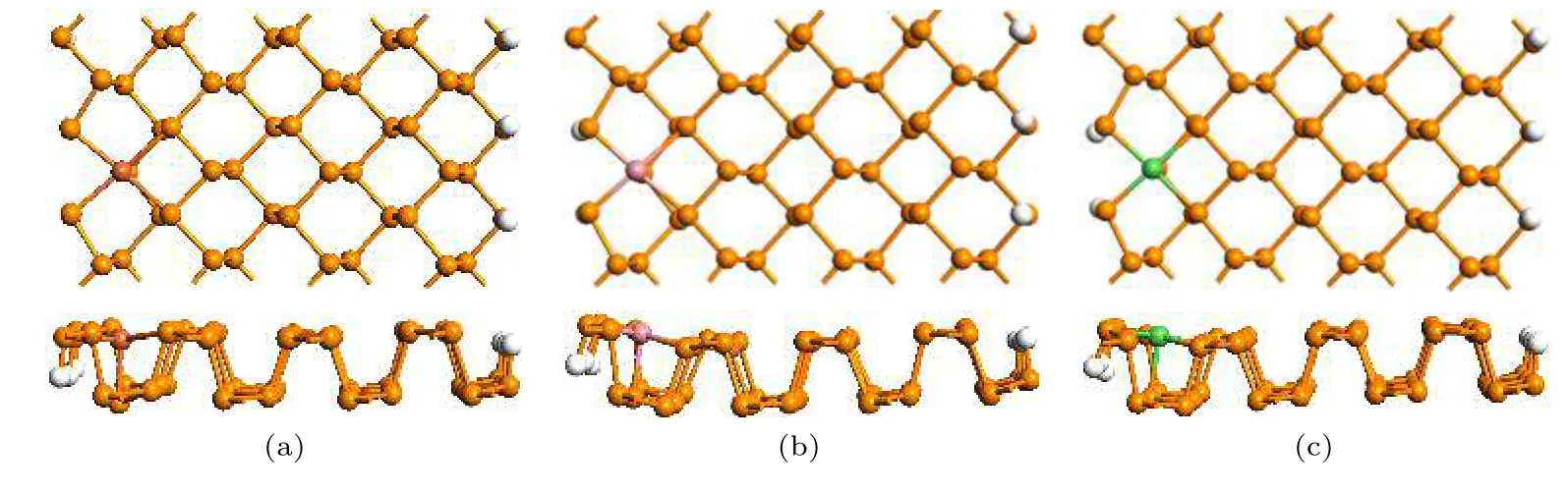
图2 模拟退火后的模型结构 (a) Fe−ZPNR; (b) Co−ZPNR; (c) Ni−ZPNRFig.2.The geometric structure after anneal simulation: (a) Fe−ZPNR; (b) Co−ZPNR; (c) Ni−ZPNR.

为了进一步研究取代掺杂结构的能量稳定性,分别取各掺杂ZPNR 的超原胞计算吉布斯自由能EG, 其定义为[42]

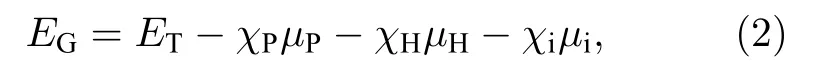
其中ET为掺杂ZPNR 超原胞的每个原子的能量;χP, χH和χi分别为P、H 和杂质原子的摩尔分数;µP, µH和µi分别为每个P、H 和杂质原子的化学势, 其中杂质原子分别为Fe, Co 和Ni.µP为磷烯中每个原子的能量, µH为氢分子中每个原子的能量, µi为体态下每个杂质原子的能量.计算结果显示, Fe−ZPNR, Co−ZPNR 和Ni−ZPNR 的吉布斯自由能分别为—0.40, —0.41, —0.40 eV.由此可见, 各掺杂ZPNR 的吉布斯自由能都为负值, 说明各掺杂ZPNR 的结构都稳定.

为了检验取代掺杂结构的热稳定性, 我们在几何优化后对其进行了Forcite 退火分子动力学模拟[43].整个模拟过程使用4 个退火循环, 并使用微正则系综.每个退火循环由初始温度300 K 升高至最高温度500 K, 然后冷却至初始温度.整个模拟过程运行8000 步, 总时间为8 ps.模拟退火后的几何结构如图2 所示, 图2(a)—(c)分别为Fe−ZPNR, Co−ZPNR 和Ni−ZPNR.与退火前的ZPNR相比, 杂质原子与周边P 原子间的键长略有变化,但没有产生局部重建.这表明所有掺杂ZPNR 的热稳定性很好.

3.2 掺杂ZPNR 的磁电子学特性

我们首先对掺杂ZPNR 进行自旋非极化计算,其对应的非磁(NM)态的能带结构和态密度(DOS)如图3(a)和图3(b)所示.图中Fe, Co 和Ni 分 别 表 示Fe−ZPNR, Co−ZPNR 和Ni−ZPNR,而ZPNR 表示未掺杂的ZPNR.图中虚线表示费米能级, 设为零.由图3 可见, 未掺杂的ZPNR 没有能带穿越费米能级, 且在费米能级附近一定能量范围内, ZPNR 的DOS 为零, 故未掺杂的ZPNR为半导体.未掺杂的ZPNR 的导带底和价带顶都位于Γ 点, 故为直接带隙半导体, 其带隙大小为1.51 eV, 这与以前的研究结果是一致的[20−24].由图3(a)可见, 掺杂ZPNR 都由于掺杂而引入了两条能带, 图中用a, b 进行了标示.Fe−ZPNR 和Ni−ZPNR 各有一条能带(即能带a)穿越费米能级,而Co−ZPNR 没有能带穿越费米能级.由图2(b)可见, Fe−ZPNR 和Ni−ZPNR 的DOS 在费米能级处都不为零, 而Co−ZPNR 的DOS 在费米能级处为零.故当处于NM 态时, Fe−ZPNR 和Ni−ZPNR为金属, 而Co−ZPNR 依然为半导体.Co−ZPNR 为间接带隙半导体, 其带隙大小为1.12 eV, 小于未掺杂的ZPNR 的带隙.由此可见, 掺杂Fe 或者Ni 原子将ZPNR 由半导体转变为金属, 而掺杂Co 原子则将ZPNR 由直接带隙半导体转变成为间接带隙半导体, 且带隙减小.

图3 ZPNR 处于NM 态的 (a) 能带结构和 (b) 态密度Fig.3.(a) The band structure and (b) density of states of ZPNRs in the nonmagnetic state.

为了更清楚地分析杂质原子对能带结构的影响, 图4 绘出了掺杂ZPNR 能带结构中能带a 的电荷密度图, 图4(a)—(c)分别为Fe−ZPNR, Co−ZPNR 和Ni−ZPNR, 等值面取0.3 |e|/Å3.由图4可见, 掺杂ZPNR 的能带a 由杂质原子起主要作用, 而起次要作用的是杂质原子附近的几个P 原子.由此可见, 能带a 正是由于掺杂而引入的杂质能带, 并导致Fe−ZPNR 和Ni−ZPNR 由半导体转变为金属, 而Co−ZPNR 的带隙小于未掺杂的ZPNR的带隙.

为了更进一步分析杂质原子中哪个轨道的电子起主要作用, 图5 绘出了掺杂ZPNR 的投影态密度(PDOS)图, 图5(a)—(c)分别为Fe−ZPNR,Co−ZPNR 和Ni−ZPNR.图中的Fe, Co 和Ni 分别表示投影到Fe, Co 和Ni 原子的PDOS, 而s,p 和d 则分别表示投影到相应杂质原子的s, p 和d 轨道的PDOS.可见, 杂质原子的PDOS 主要由其d 轨道的电子贡献, 即掺杂ZPNR 的杂质原子对电子特性起主要作用的是d 轨道的电子.

现在我们对掺杂ZPNR 进行自旋极化计算以研究掺杂诱发的磁性.定义NM 态与铁磁(FM)态之间的总能差为 ∆ E =ENM−EFM, ENM和EFM分别为各超原胞在NM 态和FM 态的总能.由表1可见, 未掺杂ZPNR 和Co−ZPNR 的总能差ΔE =0, 表明未掺杂ZPNR 和Co−ZPNR 无磁性, 基态即 为NM 态.Fe−ZPNR 和Ni−ZPNR 的总能差ΔE ＞ 0, 即ENM＞ EFM, 表明Fe−ZPNR 和Ni−ZPNR的基态是FM 态.

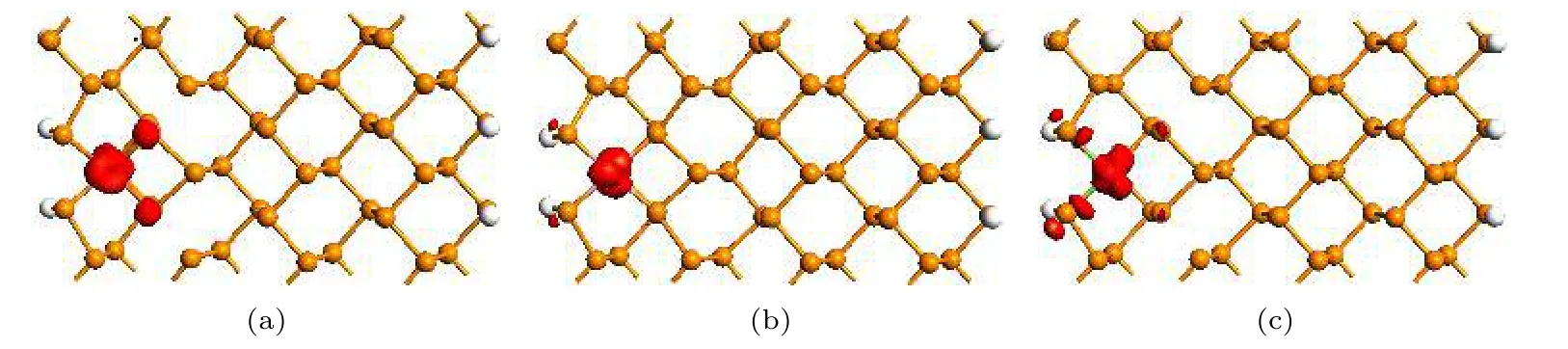
图4 部分能带的电荷密度 (a) Fe−ZPNR; (b) Co−ZPNR; (c) Ni−ZPNRFig.4.The charge density of partial band: (a) Fe−ZPNR; (b) Co−ZPNR; (c) Ni−ZPNR.

图5 掺杂ZPNRs 投影态密度 (a) Fe−ZPNR; (b) Co−ZPNR; (c) Ni−ZPNRFig.5.The partial density of states of ZPNRs: (a) Fe−ZPNR; (b) Co−ZPNR; (c) Ni−ZPNR.

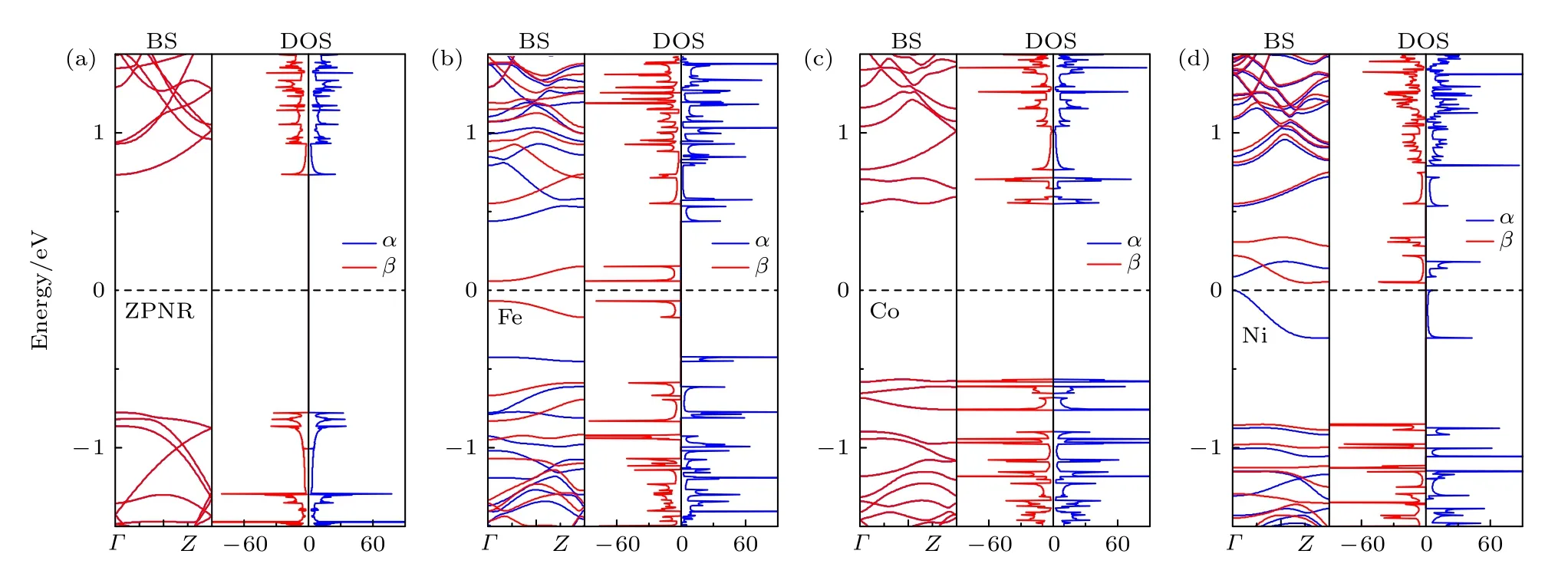
图6 ZPNR 处于FM 态的能带结构和态密度 (a) ZPNR; (b) Fe−ZPNR; (c) Co−ZPNR; (d) Ni−ZPNRFig.6.The band structure and density of states of ZPNRs in the ferromagnetic state: (a) ZPNR; (b) Fe−ZPNR; (c) Co−ZPNR;(d) Ni−ZPNR.

为了分析掺杂ZPNR 的磁电子学特性, 图6展示了掺杂ZPNR 处于FM 态的能带结构和态密度, 图6(a)—(d)分别为未掺杂ZPNR, Fe−ZPNR,Co−ZPNR 和Ni−ZPNR.图6 中蓝色实线和红色实线分别表示α 和β 自旋(下同).由图6(a)和图6(c)可见, 未掺杂ZPNR 和Co−ZPNR 的能带是简并的, 没有能带穿越费米能级, 在费米能级附近一定能量范围内, ZPNR 的DOS 为零, 故未掺杂ZPNR和Co−ZPNR 为半导体, 其带隙大小分别为1.51 和1.12 eV.能带简并这一特性结合总能差ΔE = 0,进一步表明未掺杂ZPNR 和Co−ZPNR 没有磁性.未掺杂ZPNR 没有磁性, 这一结果与之前的研究结果[32]是一致的.由图6(b)和图6(d)可见, Fe−ZPNR 和Ni−ZPNR 在费米能级附近的能带都发生了分裂, 表明Fe−ZPNR 和Ni−ZPNR 具有磁性.Fe−ZPNR 的α 和β 自旋都没有能带穿越费米能级, 且在费米能级处的态密度都为零, 故Fe−ZPNR为自旋半导体, 且为半−半导体.Fe−ZPNR 的α 和β 自旋的导带底和价带顶都位于Γ 点, 故都为直接带隙, 其带隙大小分别为0.87 和0.13 eV.Ni−ZPNR的β 自旋没有能带穿越费米能级, 但α 自旋有能带穿越费米能级, 且在费米能级处β 自旋的态密度不为零, 而α 自旋的态密度为零, 故Ni−ZPNR 为半金属.Ni−ZPNR 的β 自旋为间接带隙, 其带隙大小为0.90 eV.可见, 掺杂Fe 原子可使ZPNR 由无磁性半导体转变为磁性半导体, 而掺杂Ni 原子可使ZPNR 由无磁性半导体转变为磁性半金属.

为了分析磁性的来源, 图7 给出了掺杂ZPNR在FM 态的自旋极化电荷密度等值面图, 图7(a)—(c)分别为Fe−ZPNR, Co−ZPNR 和Ni−ZPNR.图7中红色和蓝色分别代表α 和β 自旋, 等值面取0.02 |e|/Å3.自旋极化电荷密度 ∆ ρ=ρα−ρβ, 其中 ρα和 ρβ分别表示α 和β 自旋的电荷密度.由图7(a)和图7(c)可见, Fe−ZPNR 和Ni−ZPNR 的自旋极化电荷密度的共同特点是, 在该等值面下,几乎只见到α 自旋电荷, 且自旋电荷主要分布于杂质原子, 其次分布于杂质原子附近的P 原子.因为只在纳米带左边缘掺杂, α 自旋的电荷分布在左边缘, 右边缘未见到自旋电荷, 所以Fe−ZPNR 和Ni−ZPNR 磁性状态都表现为铁磁性, 而且只能表现出FM 态, 不会出现反铁磁(AFM)态.由图7(b)可见, 在该等值面下, Co−ZPNR 没有观察到自旋极化电荷.可见Fe−ZPNR 和Ni−ZPNR 的磁性主要来源于杂质原子, 而Co−ZPNR 无磁性.

对ZPNR 磁矩计算结果表明, 未掺杂ZPNR和Co−ZPNR 超原胞的总磁矩为0µB, Fe−ZPNR和Ni−ZPNR 超原胞的总磁矩分别为1.00µB和0.89µB, µB为玻尔磁子.磁矩计算结果同样表明,对Fe−ZPNR 和Ni−ZPNR 的磁矩贡献最大的是杂质原子.Fe 和Ni 原子的磁矩分别为0.96µB和0.43µB, 分别对其超原胞的总磁矩贡献了96.0%和48.3%.由此可进一步说明掺杂Fe−ZPNR 和Ni−ZPNR 的磁性主要由杂质原子贡献.而未掺杂ZPNR 和Co−ZPNR 超原胞的总磁矩为零, 也进一步表明未掺杂ZPNR 和Co−ZPNR 没有磁性.

掺杂诱发ZPNR 的磁性, 可做如下解释.由于P 原子最外层具有5 个价电子, 每个P 原子与周边3 个P 原子成键, 即有3 个电子与周边原子的电子配对, 剩余2 个电子配对.按照能量最小原理, 原子内的电子先填充4s 层, 再填充3d 层.对于Fe, Co 和Ni 原子来说, 它们的4s 层都填充2 个电子, 而3d 层填充的电子数量分别为6, 7 和8 个.由前面的分析知道, 在掺杂ZPNR 中, 杂质原子与周边5 个P 原子成键, 且杂质原子对电子特性起主要作用的是d 轨道的电子.Fe 原子的3d 层有6 个电子, Fe 原子与周边5 个P 原子成键, 剩下1 个未配对电子.Co 原子的3d 层有7 个电子, Co 原子与周边5 个P 原子成键, 剩下的两个电子配对.而Ni 原子的3d 层有8 个电子, Ni 原子与周边5 个P 原子成键, 剩余3 个电子, 其中2 个电子配对, 剩下1 个未配对电子.正是由于在ZPNR 中掺杂Fe 和Ni 原子出现了未配对电子,才导致Fe−ZPNR 和Ni−ZPNR 具有磁性.而在ZPNR 中掺杂Co 原子没有出现未配对电子, 因此Co−ZPNR 没有磁性.

3.3 掺杂位置对磁电子学特性的影响

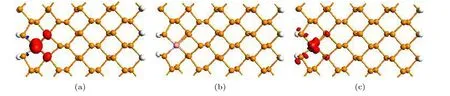
图7 自旋极化电荷密度等值面图 (a) Fe−ZPNR; (b) Co−ZPNR; (c) Ni−ZPNRFig.7.The isosurface plots of spin polarization charge density in the ferromagnetic state: (a) Fe−ZPNR; (b) Co−ZPNR; (c) Ni−ZPNR.

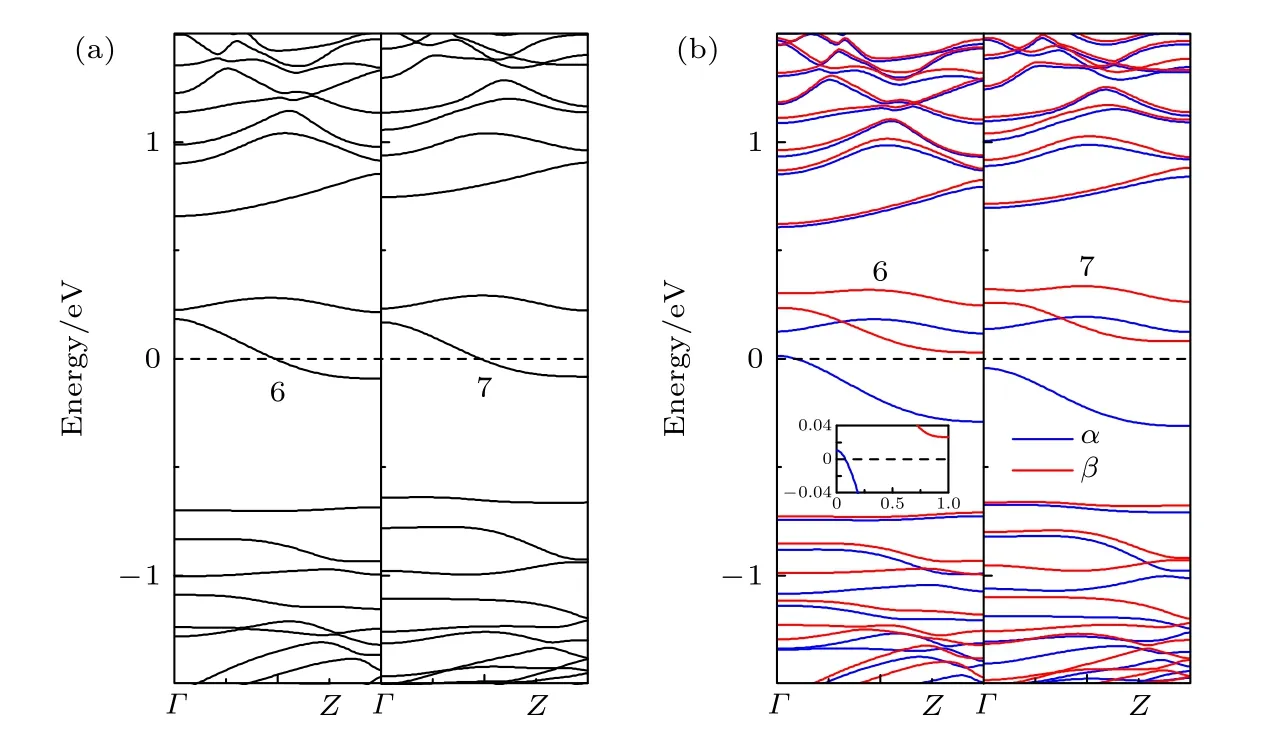
图8 改变掺杂位置时ZPNR 的能带结构 (a) NM; (b) FMFig.8.The band structure of ZPNRs with different doping position: (a) NM; (b) FM.

为了研究掺杂位置对掺杂ZPNR 磁电子学特性的影响, 在此以掺杂Ni 原子为例进行分析, 其能带结构如图8 所示, 图8(a)和图8(b)分别为NM 态和FM 态, 图8(b)中的插图为费米能级附近能带结构的局部放大图.为了说明方便, 将Ni 原子取代图1(a)中标注x, 6 和7 的P 原子的ZPNR 分别用Nix−ZPNR, Ni6−ZPNR 和Ni7−ZPNR表示.标注x, 6 和7 的P 原子分别位于第1, 第2和第3 条P 原子链靠纳米带对称中心一侧的中间位置.图8 中的6 和7 分别代表Ni6−ZPNR 和Ni7−ZPNR.结合图3(a)和图8(a)可见, 当处于NM态时, 在ZPNR 的3 个不同位置掺杂Ni 原子, 都在费米能级附近引入了两条杂质能带, 并且有一条穿越费米能级, 故ZPNR 属性不变, 都为金属.结合图6(d)和图8(b)可见, 当处于FM 态时, 在ZPNR 的3 个不同位置掺杂Ni 原子, 费米能级附近的能带都发生了分裂, 但呈现出不同的特性.Ni6−ZPNR 的磁电子学特性与Nix−ZPNR 相同,α 自旋有能带穿越费米能级, 但β 自旋没有能带穿越费米能级, 即呈现为半金属.Ni6−ZPNR 的β 自旋为直接带隙, 其带隙大小为0.74 eV.但Ni7−ZPNR的磁电子学特性与Nix−ZPNR 不同, 此时α 和β自旋都没有能带穿越费米能级, 即呈现为磁性半导体.Ni7−ZPNR 的α 和β 自旋都为间接带隙, 其带隙大小分别为0.16 eV 和 0.74 eV.由此可见, 当处于FM 态时, 在靠近纳米带边缘位置掺杂Ni 原子,ZPNR 表现为磁性半金属, 而在靠近纳米带对称中心位置掺杂Ni 原子, ZPNR 则表现为磁性半导体.

4 结 论

利用基于密度泛函理论的第一性原理方法, 研究了掺杂Fe, Co 和Ni 原子的锯齿形磷烯纳米带的磁电子学特性.研究表明, 掺杂和未掺杂ZPNR的结构都是稳定的, 未掺杂ZPNR 和Co−ZPNR的基态为NM 态, 而Fe−ZPNR 和Ni−ZPNR的基态是FM 态.当处于NM 态时, 掺杂Fe 或者Ni 原子将ZPNR 由半导体转变为金属, 而掺杂Co 原子则将ZPNR 由直接带隙半导体转变成为间接带隙半导体, 且带隙减小.发生这种转变是由于掺杂在能带结构中引入了杂质能带.处于FM 态时, 未掺杂ZPNR 和Co−ZPNR 无磁性, 掺杂Fe 原子使ZPNR 由无磁性半导体转变为磁性半导体, 而掺杂Ni 原子使ZPNR 由无磁性半导体转变为磁性半金属.Fe−ZPNR 和Ni−ZPNR 的磁性主要由杂质原子贡献.Fe−ZPNR 和Ni−ZPNR 具有磁性, 是由于在ZPNR 中掺杂Fe 和Ni 原子出现了未配对电子.而Co−ZPNR 没有磁性, 则是在ZPNR 中掺杂Co 原子没有出现未配对电子.掺杂位置对ZPNR的磁电子学特性有一定的影响, 当处于FM 态时,在靠近纳米带边缘位置掺杂Ni 原子, ZPNR 表现为半金属, 而在靠近纳米带对称中心位置掺杂Ni 原子, ZPNR 则表现为磁性半导体.该研究对于发展基于磷烯纳米带的纳米电子器件具有重要意义.