初中生逻辑推理能力的现状调查
2021-03-11严卿,喻平
严 卿,喻 平
初中生逻辑推理能力的现状调查
严 卿1,喻 平2
(1.湖北大学 数学与统计学学院,湖北 武汉 430062;2.南京师范大学 数学科学学院,江苏 南京 210046)
对中国初中生的逻辑推理能力展开调查,重点关注这一能力在年级、学校类型、性别等变量上的差异,结果如下:中国初中生初步掌握了基本的逻辑推理能力,这一能力受制于对数学知识以及逻辑形式的掌握;初中是逻辑推理能力的快速发展期,假言推理的提升幅度最大;重点中学学生逻辑推理能力优于普通中学,随着年龄增长,两类学校学生能力提升幅度差异不大;初中男女生逻辑推理能力总体上不存在差异,但男生内部存在更大的离散性.
数学核心素养;逻辑推理能力;学校差异;性别差异
1 问题提出
长久以来,“逻辑推理能力”就居于中国数学教育目标之列,这一能力的重要意义可以从两方面来认识.其一,理解数学概念、命题、证明,形成知识体系的前提.“全部数学都可以化归为逻辑”,逻辑主义学派的这一基本主张虽未能实现,但也清楚表明了逻辑之于数学的价值.其二,日常生活中,人们的语言、行为也离不开逻辑的指导,借助逻辑推理,人们可以对未见之事物进行判断、预测或还原.在2017版《普通高中数学课程标准》中,“逻辑推理”作为6个核心素养之一而提出,既是对这一能力重要价值的重申,又赋予了其“价值观念”与“品格”上新的意蕴[1].与此同时,“价值观念”与“品格”又不应看作与能力同属一个层面上的目标,而是在掌握能力的基础上,经过长期实践与反思而逐渐升华形成,因此,“能力”于教学实践而言,仍是更为直接的指向.而了解学生逻辑推理能力的现状,无疑能够让能力的培养有的放矢.
依据所使用理论框架与测量工具的不同,一些研究从不同角度对中国学生的逻辑推理能力进行了揭示.周雪兵对学业质量监测测试中与逻辑推理相关的题目进行分析后指出,江苏省初二年级学生的逻辑推理能力不存在性别上的显著差异,演绎推理水平优于合情推理等[2].程靖等从3个维度(推理类型、内容分支、高低水平)出发构建了数学推理论证能力测评框架,并基于此编制测题,研究发现,中国八年级学生合情推理整体上处于中等水平,论证推理能力处于初级水平,数学推理论证能力不存在显著的性别差异[3].綦春霞等从比较的视角出发,采用PISA的框架与测题,对中、英两国八年级学生推理能力的调查发现,英国学生在代数推理和概率推理方面的得分高于中国学生,中国学生的几何推理得分高于英国学生[4].武锡环等将信息表征、归纳识别、形成猜想、假设检验确定为影响归纳推理的4个重要因素,并据此编制测试题.在初中3个年级施测的结果显示,初二年级是数学归纳推理发展的关键期.学生在归纳推理中缺乏对得到的结论进行检验的习惯,反映出自我监控、自我反思能力的低下[5].
由于逻辑推理具有一般性的特点,不仅是数学中的思维工具,也存在于日常的语言与实践中,这种日常语言内容或纯粹符号下的逻辑推理能力是心理学工作者所关注的.这一类研究由于不存在数学知识的限制,往往涉及了不同年龄的样本,表现为对能力发展规律的揭示.另一个特点在于,通常针对的是某一种推理形式,求“专”而不求“全”.例如,李丹等人的研究指出,假言推理能力在小学三年级开始就有初步表现,初一达到掌握水平,在小学六年级到初中一年级这个阶段出现发展的加速现象,也随命题的具体内容,教学条件的变化有所不同[6].胡竹菁等调查发现,范畴三段论推理能力在初中阶段发展较快,由初中升高中时有一个较大的飞跃.另外,理科生表现优于文科生,表明推理能力受到不同学科课程训练的影响[7].黄煜烽等研究显示,初二年级是归纳推理能力迅速发展的时期,初一学生的归纳推理还依赖于具体经验的支持、往往体现为枚举而非得到新的涵义[8].
应该说,心理学领域中的研究带来的启发是多方面的.由于其不涉及数学知识,考查的是对纯粹逻辑形式的认识,对于判断学生逻辑推理上的缺陷是来自于逻辑、抑或是数学知识是有帮助的.更重要的是研究方法上的思考,例如,在评价逻辑推理能力时,是否应更多考虑对逻辑形式认识情况的考查?在数学知识背景下,能否考查不同年龄学生能力的发展变化?研究将在这两个方面尝试突破,揭示中国初中生逻辑推理能力的现状.具体研究问题如下:中国初中生逻辑推理能力处于何种水平?该能力在不同年级、学校、性别群体间存在怎样的差异?
2 研究方法
2.1 研究对象
研究样本来自江苏、江西、广东、山东.其中,江苏省的一所学校为重点中学,其余样本都来自普通中学,能够较好代表所在地区的平均水平.有效样本来源及分布情况见表1(部分学生未填写性别).
测验于学年的上学期实施.删除较多题项未作答或答案呈规律性的试卷后,回收试卷3 596份,回收率为90.08%.其中普通中学2 684人,这部分样本用于研究初中生逻辑推理能力的现状、年级及性别差异.重点中学912人,用于研究逻辑推理能力在两类学校学生间的差异.
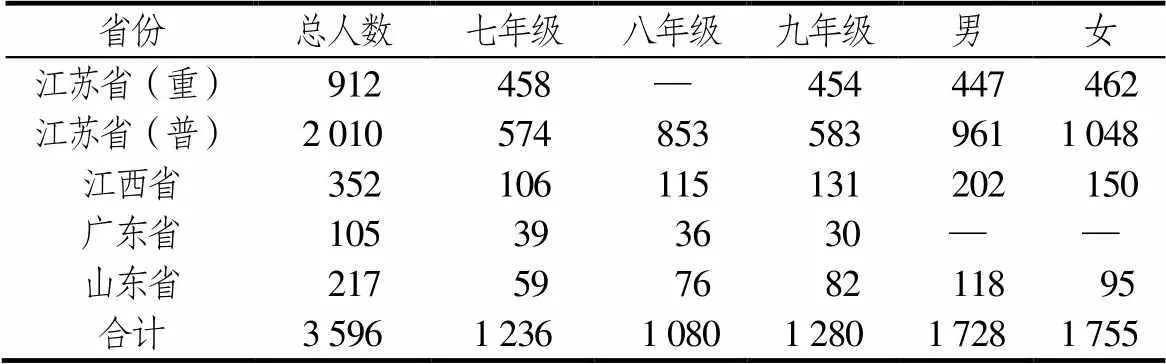
表1 样本分布情况
2.2 研究工具
调查采用严卿等编制的《初中生逻辑推理测验》[9].该测验的编制与修订过程简述如下.(1)确立评价框架.基于逻辑学对于推理的分类以及心理学关于推理能力的研究成果,把逻辑推理划分为演绎推理与合情推理两个分测验,前者包括简单推理、假言推理、选言推理、命题演算等子测验,后者包括归纳推理与类比推理,这样一来,实现了把具体推理形式作为考察的对象.(2)编制题项.对于题项的内容背景,以数学知识为主,辅以现实背景问题和符号问题,且涉及的数学知识不超出七年级上学期教材的水平,能够适用于初中3个年级.从而,该测验兼顾了逻辑推理的形式与内容两方面,又由于题目中数学内容比较简单,因而更加侧重于形式逻辑能力的考察.(3)通过先后两轮预测与修订,检验信、效度.第二轮预测后得到的结果如下:对分测验分别进行探索性因素分析的结果显示,演绎推理分测验解释变异量达到58.6%,题项的因素负荷在0.577~0.830间;合情推理分测验解释变异量为39.7%,题项的因素负荷在0.577~0.705间.除了归纳推理与类比推理的题项合并为同一个因素,其余题项基于数据抽取的共同因素与理论框架基本一致.计算测验间的相关系数,演绎推理内部4个子测验间的相关系数小于各自与演绎推理间的相关系数;演绎推理内部4个子测验与演绎推理间的相关系数,除命题演算略小外,大于各自与总测验的相关系数;演绎推理与合情推理间的相关系数小于各自与总测验的相关系数.基于以上结果,测验具有较好的结构效度.总测验的克伦巴赫系数为0.898,各子测验与分测验的系数在0.549~0.868之间,表明测验具有较好的信度.最终版测验总计22道题,全部为选择题,其分布为:简单推理4题,假言推理3题,选言推理4题,命题演算4题,合情推理7题.内容上,数学背景13题,现实背景7题,符号背景2题.每道题计2分,满分44分.
2.3 数据处理
使用SPSS 19.0软件进行数据管理及统计处理.由于调查样本较大,有可能会出现存在统计显著性而缺乏实际效果的问题,故同时也参考效应量指标来检验数据差异的实际意义.对两组数据均值差异进行显著性检验时用Cohen’s作为效应量,0.2、0.5和0.8分别对应了小、中、大的效应量.方差分析的效应存在多种估计指标,包括2、2、等,此处选择较为常用的2作为效应量,它的大小反映了自变量对因变量变异的解释程度,0.01、0.06、0.14分别对应了小、中、大的效应量[10-11].
3 研究结果
3.1 初中生逻辑推理能力总体现状
计算总测验与各分测验、子测验的均值、标准差、得分率等,结果见表2.初中生逻辑推理能力总均分为30.76,其中最低分4分,最高分44分.各子测验得分率在63.0%~82.0%之间.取总测验满分的中位数22作为参照,考察其与总分均值之间的差异,单样本检验的统计量为54.34(<0.001,Cohen’s=1.05),这说明样本不是来自于均值为22的总体.类似地,分别取各子测验、分测验满分的中位数作为参照,与测验均值做单样本检验,差异均达到显著水平(见表2).这表明,无论是在总测验还是各个子测验、分测验上,中国初中生都能够正确回答一半以上的问题.

表2 初中生逻辑推理得分的总体情况
3.2 逻辑推理能力的年级差异
以年级为自变量,逻辑推理总分及各分测验、子测验得分为因变量,进行单因素方差分析,描述性统计结果见表3.图1反映了各子测验及合情推理分测验得分随年级增长的变化趋势.

表3 初中3个年级学生逻辑推理得分的描述性统计
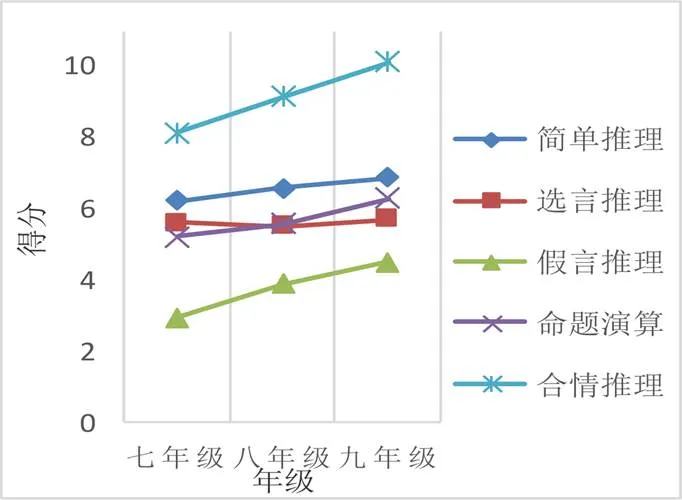
图1 逻辑推理得分的年级分布
对总分的方差分析结果显示,年级差异达到显著水平((2, 2 681)=87.69,<0.001,偏2=0.06).方差齐性检验统计量=13.10(<0.001),说明各组方差存在显著差异.选择Tamhane’s方法进行事后多重检验,八年级得分高于七年级(<0.001,Cohen’s=0.31);九年级得分高于八年级(<0.001,Cohen’s=0.33);九年级得分高于七年级(<0.001,Cohen’s=0.70).整体上看,初中生逻辑推理能力在七至八年级、八至九年级间保持着稳定的提升.
对子测验与分测验得分的方差分析结果如下.在简单推理上,年级差异达到显著水平((2, 2 681)=36.02,<0.001,偏2=0.03);八年级得分高于七年级(<0.001,Cohen’s=0.23),九年级得分高于八年级(<0.001,Cohen’s=0.19),九年级得分高于七年级(<0.001,Cohen’s=0.43).在假言推理上,年级差异达到显著水平((2, 2681)=146.74,<0.001,偏2=0.10);八年级得分高于七年级(<0.001,Cohen’s=0.50),九年级得分高于八年级(<0.001,Cohen’s=0.33),九年级得分高于七年级(<0.001,Cohen’s=0.88).在选言推理上,年级差异没有达到显著水平((2, 2 681)=1.65,>0.05).在命题演算上,年级差异达到显著水平((2, 2 681)=45.46,<0.001,偏2=0.03);八年级得分高于七年级(P<0.01,Cohen’s=0.14),九年级得分高于八年级(<0.001,Cohen’s=0.32),九年级得分高于七年级(<0.001,Cohen’s=0.48).在演绎推理上,年级差异达到显著水平((2, 2 681)=70.43,<0.001,偏2=0.05);八年级得分高于七年级(<0.01,Cohen’s=0.27),九年级得分高于八年级(<0.001,Cohen’s=0.31),九年级得分高于七年级(<0.001,Cohen’s=0.62).在合情推理上,年级差异达到显著水平((2, 2 681)=71.42,<0.001,偏2=0.05);八年级得分高于七年级(<0.001,Cohen’s=0.31),九年级得分高于八年级(<0.001,Cohen’s=0.29),九年级得分高于七年级(<0.001,Cohen’s=0.61).总体而言,除选言推理外,其余子测验及分测验得分都保持了持续的增长.简单推理及合情推理上保持着稳定的增长速度,假言推理在七至八年级发展较快,命题演算的快速发展出现在八至九年级.
3.3 逻辑推理能力的学校差异
研究前述部分目的在于探讨一种普遍性的逻辑推理能力现状,样本的选择重点关注代表性,故将重点中学样本数据排除在外.按照通常的认识,重点中学学生的逻辑推理能力理应优于普通中学,问题在于这种优势是否能达到一种统计学意义上的差异?此外,随着年级的提升,重点中学和普通中学的差异会有一种怎样的变化?如果说七年级时的差异代表了一种生源上的区别,那么九年级时的差异则可以反映出学校教育对于逻辑推理能力的影响.以年级(七年级、九年级)、学校类型(重点、普通)为自变量,分别以总测验、分测验、子测验得分为因变量,进行2×2方差分析.描述性统计结果见表4,两类学校样本在两个年级的总分分布见图2.
对总分的方差分析结果显示,学校类型主效应显著((1, 2 512)=284.67,<0.001,偏2=0.10);年级主效应显著((1, 2 512)=155.83,<0.001,偏2=0.06);学校类型与年级的交互作用显著((1, 2 512)=20.79,<0.001,偏2=0.01).虽然交互作用显著,但效应量仅为0.01,说明两类学校学生逻辑推理能力在七至九年级的提升幅度实际差异并不大.简单效应分析显示,七年级(<0.001,Cohen’s=0.97)和九年级(<0.001,Cohen’s=0.48)时,重点中学得分都显著高于普通中学.虽然差异有一定减少,考虑到天花板效应,这种减小能否看作学生逻辑推理能力的缩小,是值得商榷的.
对于各分测验与子测验,方差分析结果简述如下:学校类型主效应均达到显著水平,效应量偏2在0.03(选言推理)至0.08(假言推理)之间;学校类型与年级的交互作用,除选言推理外,均达到显著水平,但效应量最高仅为0.01(简单推理).从而,对分测验与子测验得分进行方差分析的结果,与总分基本上是一致的.

表4 两类学校学生逻辑推理得分的描述性统计
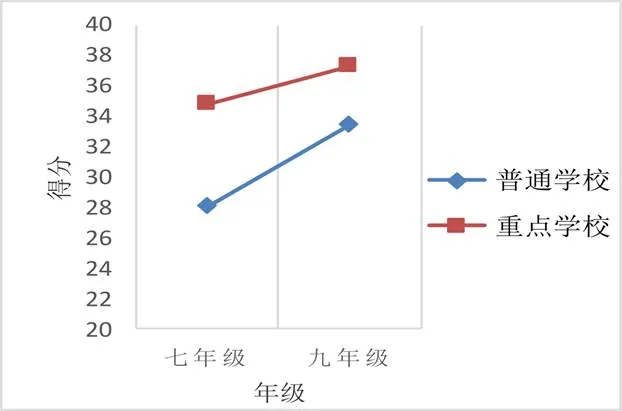
图2 两类学校样本在两个年级的总分分布
3.4 逻辑推理能力的性别差异
性别差异是逻辑推理能力研究中惯常涉及的一个问题,这里将年级因素一并考虑在内,考查随年级变化,性别差异的变化情况.以年级、性别为自变量,分别以总测验、分测验、子测验得分为因变量,进行3×2方差分析.描述性统计结果见表5,男、女生总分在3个年级的分布见图3.
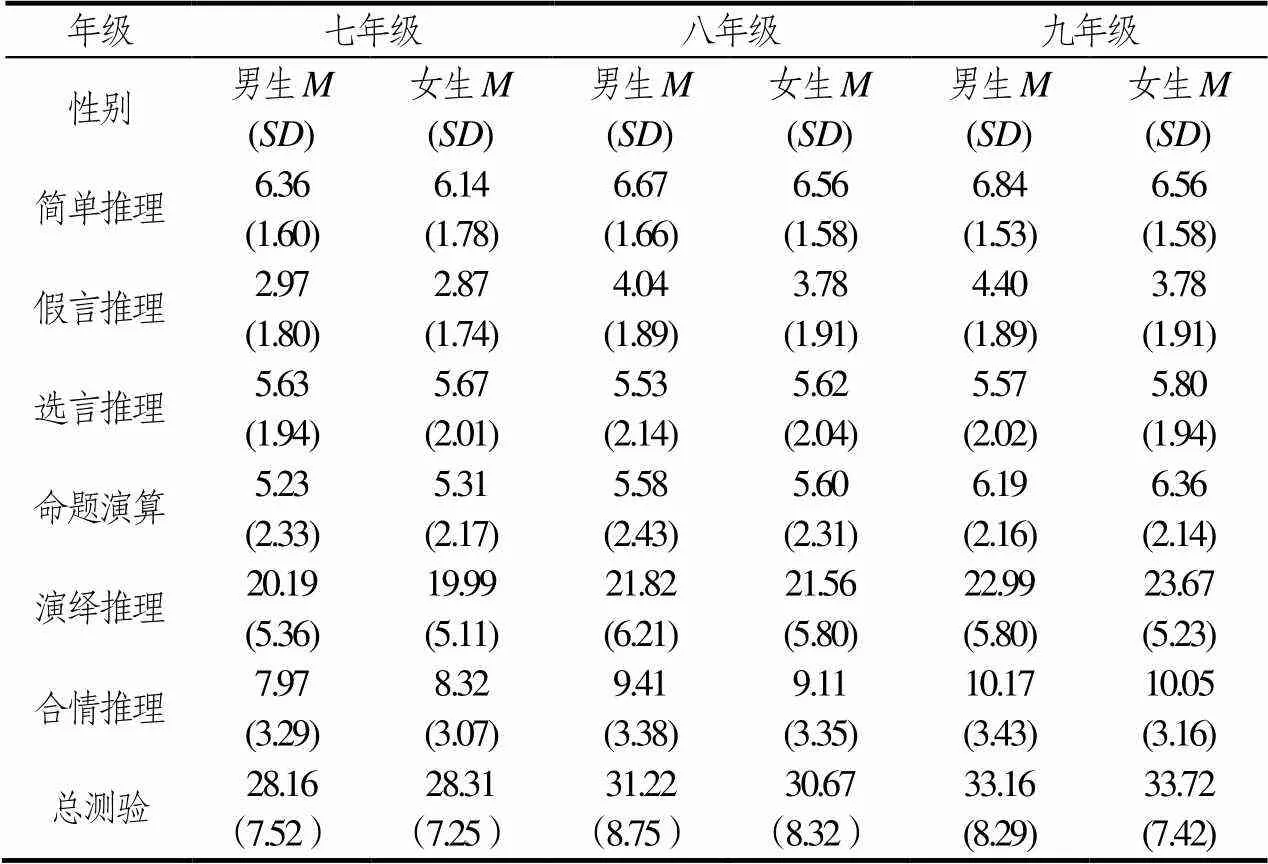
表5 男女生逻辑推理得分的描述性统计
对总分的方差分析结果显示,性别主效应不显著((1, 2 599)=0.03,>0.05);年级主效应显著((2, 2 599)=81.79,<0.001,偏2=0.06);性别与年级的交互作用不显著((2, 2 599)=1.14,>0.05).由此可见,初中阶段男、女生逻辑推理能力是十分接近的,且这一点并不随年级提升而改变.
对于各分测验与子测验,除假言推理外,性别主效应均不显著,性别与年级的交互作用均不显著.假言推理子测验性别主效应不显著,性别与年级的交互作用显著(<0.05),但效应量偏2仅为0.003.从而,对分测验与子测验得分进行方差分析的结果,与总分基本上是一致的.
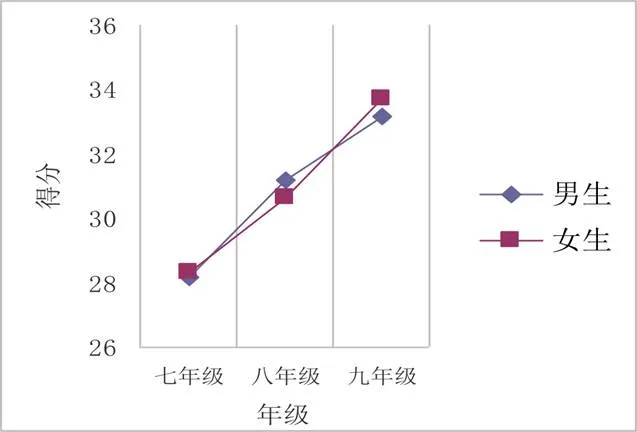
图3 男女生样本在3个年级的总分分布
4 分析与讨论
4.1 对初中生逻辑推理能力总体现状的讨论
依据研究结果,初中生在各子测验上的得分率均超过了60%,单样本检验的结果表明,各子测验均分都显著高于满分中位数.考虑到研究所用测验是对各推理形式比较直接的考查,涉及到的数学知识也比较简单,可以认为,中国初中生初步掌握了基本的逻辑推理能力.为了能够更加客观认识这一结果,还需与数学教育及心理学领域中的有关研究结果进行比较.
心理学中的研究通常针对某一种推理能力类型.李国榕等调查发现,三段论第一格的得分率在初一、初二、初三依次为76%、80%、80%[12].贾蕊调查发现,对于两选言肢的抽象任务,初中3个年级学生得分率分别为65.91%、65.91%、75.00%[13].李丹等分别调查了初中生在4种假言推理格式中的得分率,其中否定前件在不同年级的得分率分别为76%、81%、85%;否定后件分别为73%、78%、83%[6].这些研究在内容背景上都是现实背景,或符号背景.研究中,一方面设计了与心理学研究类似的现实或符号背景问题,其得分率与对应的心理学研究是比较接近的.例如t3(三段论第一格)得分率分别为74.7%、81.0%、88.9%,t10(两选言肢选言推理)得分率为67.4%、69.3%、72.3%.另一方面,研究更多题目属于数学知识背景,其得分率明显低于相同逻辑形式的现实或符号背景问题.例如t4(三段论第一格)在3个年级得分率分别为61.7%、70.0%、73.1%,t9(两选言肢选言推理)在3个年级得分率分别为62.0%、58.2%、62.5%,t6(否定前件与否定后件的假言推理)在3个年级得分率分别为29.3%、62.1%、69.0%.这一对比充分表明,仅仅对于逻辑形式的认识并不足以确保能够顺利进行数学推理,即便涉及到的数学知识并不困难.这也解释了为何一些逻辑思维训练未能提升学生的数学推理能力[14].因此,相比心理学中的研究,研究所揭示的能力现状对数学学习与教学有着更直接的参考价值.
与数学教育领域中的已有研究相比,研究结果既表现出了共性,也有一些差异.例如,如何否定一个假言命题是许多研究共同关注的一个问题.美国NAEP研究项目,英国Hoyles等开展的大规模研究等都设计了该类任务[14-15].从得分情况上来看,正确率均不及40%,且前者的样本是11年级学生.而在研究中,t15(假言命题的否定)在3个年级得分率分别为48.1%、57.7%、70.3%.虽然已属低得分率,但远高于国外研究.一方面,体现出中国学生逻辑推理能力的优势;另一方面,也反映出学生在这类任务上的困难确实具有普遍性.从样本的选项来看,超过30%的学生选择了否定前项的同时肯定后项的答案,这体现出一种逻辑思维上的缺陷.又如,对于归纳推理,一些研究指出,初中生缺乏对猜想到的结论进行反思与检验的意识与能力[3,5].研究验证了这一现状.t20(归纳推理)的得分率仅为49.3%,错误的原因在于依据1~2个个案便得出结论,缺乏验证的意识.如果进一步分析这一问题,实际上反映出学生对于归纳推理的“或然性”认识不足.近年来,数学课程、教学中对合情推理的重视在不断加强,在教材中,许多概念、法则被设计为通过归纳或类比引出[16].然而,如果教学中对归纳得到的结论经常不加证明,或归纳的结果“永远”都是正确的,难免会导致学生对归纳思维形成错误认识.
4.2 对初中生逻辑推理能力年级差异的讨论
对年龄差异的研究,通常旨在揭示出一种能力发展的内在生理规律,这一规律往往表现为发展的关键年龄阶段.虽然由于研究工具的差异,不同研究的结果很难进行直接的比较,但初中阶段是逻辑推理能力发展的关键期,则是一个普遍的结论.例如,林崇德将中学生论证推理能力划分为4个水平,包括直接推理水平、间接推理水平、迂回推理水平、按照一定数理逻辑格式进行综合性推理的水平.调查发现,初一和初二、高一和高二年级之间成绩差异达到了显著水平,初二和高二是中学生数学推理能力发展的转折点[17].孙敦甲研究发现,中学数学逻辑思维的发展是从形象抽象思维到形式抽象思维,最后向着辩证抽象逻辑思维发展.初二与初三、初三与高一、高一与高二年级间的差异均达到非常显著的水平,可见这段时间发展十分迅速[18].研究结果显示,在除选言推理外的子测验中,年级差异均达到了显著水平,从而支持了已有研究的结论.同时也必须注意,这一发展不仅是生理因素所导致的,也不能忽视学校教育起到的作用.在《义务教育数学课程标准(2011年版)》中,对假言命题及推理做出了比较详细的规定.例如,“知道原命题成立其逆命题不一定成立”“了解反例的作用”[19],这样安排是合适的.研究结果显示,假言推理得分的年级差异在各子测验中最大.因此,为了全面提高初中生的逻辑推理能力,在课程标准及教材中还应考虑更加广泛渗透各类逻辑推理内容.
4.3 对初中生逻辑推理能力学校差异的讨论
逻辑推理能力的学校差异,反映了逻辑推理能力与学业成绩之间的紧密联系.研究结果表明,重点中学的逻辑推理得分显著高于普通中学.即便将数学知识背景的题项排除在外,仅考虑现实背景或符号背景的9道题,除t2外,学校类型差异也全部达到了显著水平(效应量Cohen’s在0.14~0.34之间).因此,重点中学与普通中学的一个区别即是学生逻辑推理能力的不同,这也可以认为是导致学业成绩差异的因素之一.陈昊使用与研究相同的测验考查了八年级学生逻辑推理能力与认知结构之间的关系,结果发现二者呈显著正相关,相关系数达到0.515,从另一个角度验证了研究的这一结论[20].当前,随着核心素养培养目标的提出,如何协调提升成绩与培养能力间的关系成为一个新的命题.研究的结果表明,这两个目标是一致的,培养逻辑推理能力可以看作提升学业成绩的一个途径.
此外,依据研究结果,两类学校学生的逻辑推理能力在七~九年级间的提升程度是比较接近的.但这并不意味着普通中学对逻辑推理能力的培养已经足够,如果将重点学校得分作为一个参照,普通中学九年级得分尚不及前者七年级,更加凸显出加强逻辑推理能力培养的紧迫性.
4.4 对初中生逻辑推理能力性别差异的讨论
“性别平等”是“教育公平”的内在要求之一,因而性别也是数学能力研究中一个颇受关注的变量.研究结果显示,初中生逻辑推理能力不存在显著性别差异,这一结果与近年来的几项有关研究是一致的[2,3,21].与这些研究相比,研究还考查了3个年级性别差异的变化情况,结果显示男女生逻辑推理能力随年级增长的变化趋势也是高度一致的.另一方面,所谓“不存在显著差异”是基于均值比较的结果,如果关注男女生得分的方差变化,可以发现男生方差始终高于女生,且差距随着年级的提升在变大.这一结果支持了“男性更大变异假设”,该理论由Ellis提出,指男性在身体素质、心理特点和智力方面的个体差异要大于女性.郝连明等对初二学生数学学业成绩的研究支持了这一理论,研究是从另一个角度的再次验证[22].从而,就教师而言,对于学生的逻辑推理能力,一方面不应持有先入为主的性别偏见,另一方面,也需认识到男女生在该能力上的不同特征.
5 结论与思考
研究结论:(1)中国初中生初步掌握了基本的逻辑推理能力.这一能力受制于对数学知识的掌握,对逻辑形式本身的认识并不足以确保数学推理的顺利进行;也受制于对逻辑形式的掌握,例如如何否定假言命题,对归纳推理“或然性”的认识等.(2)初中是逻辑推理能力的快速发展期.假言推理的发展幅度最大,这一点可以看作是课标中强调的结果.(3)重点中学学生逻辑推理能力优于普通中学,随年龄增长,两类学校学生能力提升幅度区别不大.(4)初中男女生逻辑推理能力总体上不存在差异,但男生内部存在更大的离散性.
以上结论受制于下面几点思考:(1)研究中的逻辑推理问题侧重于推理的形式方面,内容知识上比较简单.显然,对于推理形式的认识是解决更加复杂、更多步骤推理问题的必要条件,但前者与后者究竟在多大程度上相联系,研究涉及不深,尚需要进一步的研究.(2)研究以量化方法为主,虽然能够发现规律和现象,但在解释上有所不足,要对原因进行追溯,一方面还需展开质化研究,另一方面也有必要诉诸神经科学的研究成果.
[1] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018:4.
[2] 周雪兵.基于质量监测的初中学生逻辑推理发展状况的调查研究[J].数学教育学报,2017,26(1):16-18.
[3] 程靖,孙婷,鲍建生.我国八年级学生数学推理论证能力的调查研究[J].课程·教材·教法,2016,36(4):17-22.
[4] 綦春霞,王瑞霖.中英学生数学推理能力的差异分析——八年级学生的比较研究[J].上海教育科研,2012(6):93-96.
[5] 武锡环,李祥兆.中学生数学归纳推理的发展研究[J].数学教育学报,2004,13(3):88-90.
[6] 李丹,张福娟,金瑜.儿童演绎推理特点再探——假言推理[J].心理科学,1985,8(1):6-12.
[7] 胡竹菁.演绎推理的心理学研究[M].北京:人民教育出版社,2000:219-222.
[8] 黄煜烽,杨宗义,刘重庆,等.我国在校青少年逻辑推理能力发展的研究[J].心理科学,1985,8(6):28-35.
[9] 严卿,黄友初,罗玉华,等.初中生逻辑推理的测验研究[J].数学教育学报,2018,27(5):25-32.
[10] 郑昊敏,温忠麟,吴艳.心理学常用效应量的选用与分析[J].心理科学进展,2011,19(12):1 868-1 878.
[11] 胡竹菁,戴海琦.方差分析的统计检验力和效果大小的常用方法比较[J].心理学探新,2011,31(3):254-259.
[12] 李国榕,胡竹菁.中学生直言性质三段论推理能力发展的调查研究[J].心理科学,1986,9(6):39-40.
[13] 贾蕊.选言推理能力的发展性研究[D].曲阜:曲阜师范大学,2007:30.
[14] Harel G, Sowder L. Toward comprehensive perspectives on the learning and teaching of proof [M] // F Lester. Second handbook of research on mathematics teaching and learning. Greenwich: Information Age Publishing, 2007: 805-842.
[15] Hoyles C, Küchemann D. Students’ understandings of logical implication [J]. Educational Studies in Mathematics, 2002, 51 (3): 193-223.
[16] 严卿,胡典顺.中国和日本初中数学教材中问题提出的比较研究[J].数学教育学报,2016,25(2):20-25.
[17] 林崇德.学习与发展:中小学生心理能力发展与培养[M].北京:北京师范大学出版社,2003:365-367.
[18] 孙敦甲.中学生数学能力发展的研究[J].心理发展与教育,1992,8(4):52-58.
[19] 中华人民共和国教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012:6.
[20] 陈昊.初中生数学认知结构与逻辑推理能力关系的研究[D].南京:南京师范大学,2018:42.
[21] 周宇剑.中学生数学基本技能水平的调查研究[J].数学教育学报,2012,21(6):46-49.
[22] 郝连明,綦春霞.基于初中数学学业成绩的男性更大变异假设研究[J].数学教育学报,2016,25(6):38-41.
Comparative Study of Chinese and French College Entrance Examination Mathematics Tests from the Perspective of Core Literacy: With a Focus on the Chinese and French College Entrance Examination Mathematics Items from 2015 to 2020
ZHANG Yu-huan, ZHOU Xia, CHEN Shuang
(School of Mathematics and Statistics, Henan University, Henan Kaifeng 475004, China)
The Ministry of Education has made it clear that the examination guidelines will be used by 2022. By then, the high school mathematics curriculum standards will play more important role for the item development of college entrance examination. It is possible that the core mathematical literacy will be increasingly and explicitly reflected in the college entrance examination. Based on the core literacy evaluation method, this study analyzed items in the science and mathematics focused version of the college entrance examinations in China from 2015 to 2020 and the items of the local college entrance examinations in France. In this analysis, we have used multivariate statistical analysis methods, such as correspondence analysis, cluster analysis, correlation analysis to investigate and compare the core literacy of China and France on overall distribution, year-by-year change, the degree of correlation and distribution. The findings from the analysis have several implications for item development in the college entrance examination: pay attention to rational thinking to embody logic; strengthen the application of mathematics to embody practicality; strengthen the exploration of mathematics to embody the process; and pay attention to mathematics culture to embody the cultivation of humanity.
core literacy; France mathematics examinations; college entrance examination items; multivariate statistics
G633.6
A
1004–9894(2021)01–0049–05
严卿,喻平.初中生逻辑推理能力的现状调查[J].数学教育学报,2021,30(1):49-53.
2020–10–27
国家社会科学基金教育学一般项目——中学生学科核心素养的评价研究(BHA170150)
严卿(1987—),男,湖北武汉人,博士,讲师,主要从事数学课程与教学论研究.
[责任编校:周学智、陈隽]
