核心素养视角下中法高考数学试题的比较研究——基于2015—2020年中国和法国高考数学试卷
2021-03-11张玉环
张玉环,周 侠,陈 爽
核心素养视角下中法高考数学试题的比较研究——基于2015—2020年中国和法国高考数学试卷
张玉环,周 侠,陈 爽
(河南大学 数学与统计学院,河南 开封 475004)
教育部明确2022年前全面取消考试大纲,这意味着高中数学课程标准对于高考命题的指导性将有所加强,其所明确的数学核心素养在高考中的体现将更加显著.因此,选取核心素养评价框架,对2015—2020年中国理科数学全国Ⅰ卷与法国本土高考理科试卷考查的核心素养进行量化,利用对应分析、聚类分析、相关分析等多元统计分析方法,进行关于整体分布、逐年变化、关联程度、受重视程度、相关程度、集中程度的中法核心素养考查对比,并基于分析结果提出高考命题建议:注重理性思维,体现逻辑性;强化数学应用,体现实践性;加强数学探索,体现过程性;关注数学文化,体现育人性.
核心素养;法国数学;高考试题;多元统计
1 问题提出
自2014年9月国务院印发《国务院关于深化考试招生制度改革的实施意见》以来[1],新一轮考试招生制度改革已全面启动.高考内容改革是高考改革的重点,也是难点.2019年6月,国务院办公厅发布《关于新时代推进普通高中育人方式改革的指导意见》,明确2022年前全面取消考试大纲,高考要以普通高中课程标准和高校人才选拔要求为依据[2].这代表着高中课程标准要指导高考命题.教育部《关于全面深化课程改革落实立德树人根本任务的意见》指出,学科核心素养是育人价值的集中体现,是学生通过学科学习而逐步形成的正确价值观念、必备品格和关键能力[3].《普通高中数学课程标准(2017年版)》(以下简称《课标》)的重要成果之一是明确了数学核心素养的概念[4].2020年,教育部考试中心正式发布《中国高考评价体系》,明确了学科素养是高考着重考查的内容之一[5].
比较研究是高考试卷研究常用的方法.通过比较不同年份的试卷,可以发现中国高考的考查特点与发展趋势.从国际视野来看中国高考,更能探究出中国在素养考查方面的侧重点与不足处,为高考内容改革提供建议.蔡元培先生认为:在世界各国之中,法国文化与中国最相契合[6].在教育背景方面,法国与中国较为相似,都经历了多次高考改革.现今,其高考体系较为完备与成熟.法国教育为数学界培养了众多人才,比如现代许多菲尔兹奖得主来自法国,也是因此,法国被称为“伟大数学家摇篮”,可见其教育制度有一定的优越性与借鉴价值.而现今阶段,对法国高考的研究以定性分析居多,且多是关于高考制度与其它学科,如龚妙昆对法国会考制度简介[7].国内目前对于法国高考数学试题的分析较少,比如胡凤娟结合2014—2018年考题对法国主题式命题进行分析[8],张玉环等基于2015—2019年试题从难度视角对中法试题进行比较[9].目前没有基于核心素养视角对中法高考数学试题进行比较研究的文献.为此,研究者在核心素养评价框架的基础上,运用多元统计方法分析中法高考试题,并在分析六大核心素养的基础上,立足高考数学学科素养的层面提出高考命题建议.
2 研究设计
中国《课标》提出数学学科的6个学科核心素养:数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析[4].相应地,法国2019年发布的《高中数学课程标准》中也明确提出高中生必备的6个能力,即探究、建模、表征、推理、计算、交流[10].其中,探究能力是通过实验,尤其是借助于一些软件工具进行信息的收集整理与探究.而中国的数据分析是指针对研究对象获取数据,运用数学方法对数据进行整理、分析和推断,形成关于研究对象知识的素养.从内容上看,二者考查目标较为相似.法国的建模能力要求学生建立数学模型,并能判断模型在现实应用的有效性.这与中国的数学建模素养可相互对应.法国的表征能力要求学生能选择合适的内容模块(数字、代数、几何……)改变表达方式,这与中国的数学抽象素养有相通之处.数学抽象是指通过对数量关系与空间形式的抽象,得到数学研究对象的素养,同样是用数学语言表达事物.同时,中国的直观想象素养在此也有所体现.直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.法国的表征包含借助几何形式来改变表达方式.法国的推理能力是通过论证,阐释不同的解决方法,得到部分结果且对其分析、检验.这与中国的逻辑推理素养类似,逻辑推理是指从一些事实和命题出发,依据规则推出其它命题的素养.二者都是通过分析论证体现出数学严谨的特点.法国的计算能力是指应用信息技术和运用技巧、算法进行计算.中国与之相对应的素养为数学运算,数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.两者都是借助运算解决问题.法国的交流能力是指口头或者书面叙述运算结果,解释运算过程,这与数学建模中用数学语言表达现实世界、感悟数学与现实之间的联系这一要求有异曲同工之处.通过对法国的能力与中国的核心素养内容上的对比,发现二者有一定的相通性,在一定程度上可以相互对应,因此,能够使用同一评价标准对二者进行比较.由于比较的目的是评价中国高考,为中国的高考改革提供建议,因此,采取中国核心素养的表达与量化框架,对两国高考题进行量化对比.
2.1 评价框架
关于核心素养在题目中的评价,对题目的定性分析较多.定量分析模型中认可度较高的是喻平基于知识学习的3种形态,汲取布卢姆模型、PISA模型的长处建立的评价框架,将6个核心素养的水平分为知识理解、知识迁移与知识创新3个水平,该框架具有较强的操作性[11].李作滨以2018年高考试卷中的具体题目为例,分析了核心素养的考查情况[12].俞梦飞、章飞根据核心素养的水平与表现,在喻平的基础上建立了核心素养评价框架,并利用该框架分析了2018、2019年江苏省数学高考试卷[13].李华、胡典顺按照喻平的划分标准创建了数学核心素养评价指标体系,对各核心素养水平层次的评价标准进一步细化,研究了2019年高考全国卷的核心素养考查[14].两个框架可操作性都较强,由于研究对象是中法试卷,二者的能力与素养虽然有一定对应性,但在考查方式及表现形式上仍有所不同.俞梦飞、章飞的评价框架涉及到素养的具体表现,用其对法国试卷进行分析会造成较大误差.因此,选择李华等人细化的评价标准.
2.2 研究对象
为使研究结果有代表性,中国的研究对象选取适用考生最多的全国Ⅰ卷,以理科2015—2020年试卷为例.与之相对应,法国选择法国本土试卷,由于疫情原因,法国2020年高考取消[15],因此选取2015—2019年理科试卷[16].对于选做题的处理,中国两道或三道选做题由学生自由选择,考查分值在整套题中所占比例较小,且考查题数与形式类似,因此分析选做题的核心素养,作平均处理.法国两道选做题分别为专业选做与非专业选做,针对考生类型不同,并且两道题所占分值较大,在考查内容、考查形式上有很大不同.因此,将“必做题+不同的选做题”看作不同套试卷,即“必做题+非专业选做题”(简称非专业选做试卷)、“必做题+专业选做题”(简称专业选做试卷).
2.3 研究方法
2.3.1 编码方法
李华等人的评价框架采用“字母+数字”代表核心素养的不同水平,以此对试题进行编码.核心素养评价指标具体见表1.
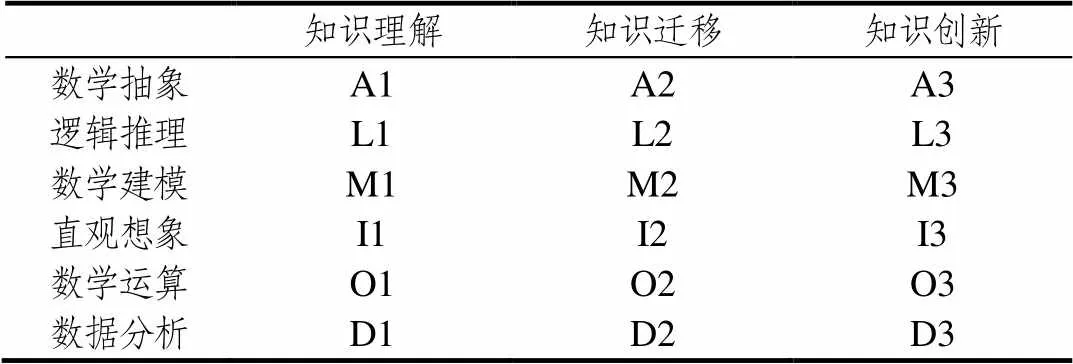
表1 核心素养评价指标
按照上述方式对中法试卷的所有题目进行编码.由于法国题目只有大题分值,无小题具体分值划分,故采用将大题分值按照包含小题数目平均到各题的方式计算.法国试卷总分20分,共4道大题.因此,每道大题的分值较低,划分到各考查素养的分值较小.为降低量化难度,避免出现较大误差,采取先将20分的试卷等比转化为100分试卷,再对每道题考查素养按照考查侧重程度以分数方法计值.下面举例说明具体的编码方法.
例1 (2020全国Ⅰ卷)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( ).

例1考查正四棱锥的相关性质,解题的关键在于将实物模型抽象为几何图形,难点在于找到其内在等量关系.这道题从现实情境出发,具有较强的抽象性,要灵活运用正四棱锥的几何性质与勾股定理,考查了知识创新水平的数学抽象素养.推理方面的要求是能理解相关概念的逻辑关系,采用常见的逻辑推理方法解决问题,重点考查知识迁移水平的逻辑推理.由于解题关键是将胡夫金字塔转化为正四棱锥模型,利用相关知识解决问题,因此,重点考查的素养为直观想象与数学建模.其中,对直观想象的素养要求为能够通过借助图形将现实问题转化为数学问题,用数形结合的思想去探讨问题本质,处理现实问题,属于知识创新水平的考查.数学建模素养的考查要求是能在新的情境中运用多种知识建立合适的数学模型来解决常规性复杂问题,属于知识迁移水平的考查.难点在于借助题中隐含的勾股定理建立等量关系,涉及大量计算.要求学生能够达到在新的情境中理解运算对象,运用运算法则和运算技巧解决常规性复杂问题,是知识迁移水平的考查.该题共计5分,考虑到该题对各素养考查的程度,将此题编码为A3—0.75,L2—0.75,M2—1,I3—1.25,O2—1.25.
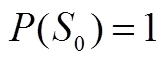
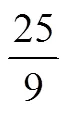
2.3.2 数据分析方法
针对中法高考试题核心素养考查的量化分析数据,采用多元统计分析方法进行分析,借助对应分析、聚类分析、相关分析等方法,进行基于整体分布、逐年变化、关联程度、受重视程度、相关程度、集中程度的中法核心素养考查对比.
3 研究过程与结果
3.1 基于整体分布的中法核心素养考查对比
按照李华等人的划分标准,以2020年中国卷为例.先统计该套试题中每小题的6个核心素养考查水平及所占分值,如第一题考查数学抽象与数学运算素养,总分值5分.其中对数学抽象的考查为知识理解水平,所占分值为2分,对数学运算的考查为知识理解水平,所占分值为3分.依此法将试卷中所有题目的素养考查进行划分,随后计算出各素养水平考查分值在试卷总分(即150分)中所占比值,汇总得到该套试卷18个核心素养指标的比重分布情况,并将各素养下3个水平的数值相加得到数学抽象(A)、逻辑推理(L)、数学建模(M)、数学运算(O)、直观想象(I)、数据分析(D)六大核心素养在该试卷的考查比重.将2015—2020年中国卷得到的数据平均处理,作为中国卷核心素养的考查比重.法国卷同样对2015—2019年的数据作平均处理,作为法国试卷核心素养的考查比重,以此对中法核心素养考查情况作整体分析,见表2.
为直观呈现中法高考试题核心素养考查的整体分布,结合表2中数据绘制全国卷、法国Ⅰ卷与法国Ⅱ卷各水平核心素养的分布情况圆环图,如图1.结合表中数据及图形分布不难发现,中法试卷在核心素养考查方面,都着重于数学运算、逻辑推理与数学抽象的考查.不同点在于,中国更注重直观想象素养的考查,法国则更注重数学建模与数据分析的考查.法国这三大核心素养的考查则较为均衡.从核心素养考查层次来看,数学抽象与数学运算素养以知识迁移水平为主,知识理解水平为辅,知识创新水平涉及较少.逻辑推理素养则是知识迁移水平为主、知识创新水平次之、知识理解水平最少.直观想象核心素养考查比例中国大于法国,且考查水平更高.数学建模核心素养考查法国多于中国,二者都以知识迁移水平为主,全国卷知识创新水平题目远多于知识理解水平,法国对知识创新和知识理解水平考查相似.数据分析素养法国考查更多,以知识迁移水平为主,知识创新水平为辅,中国则集中于知识迁移水平的考查.

表2 核心素养考查比重
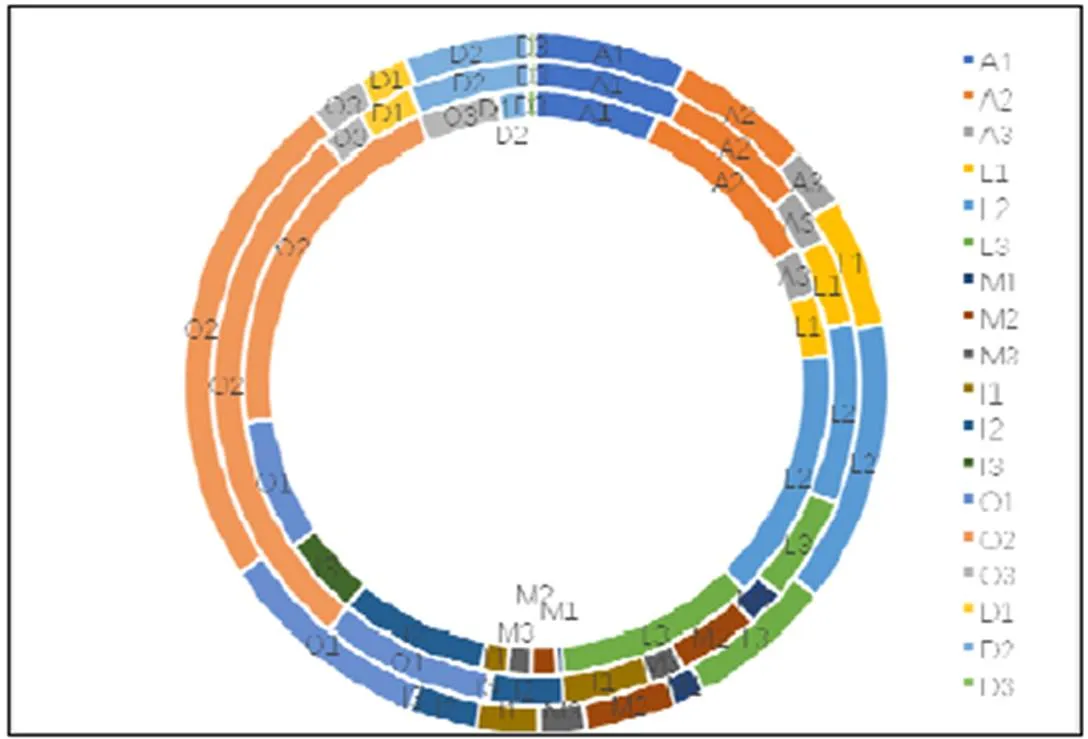
图1 各水平核心素养的分布
3.2 基于逐年变化的中法核心素养考查对比
为直观呈现中法高考核心素养的逐年变化情况,对2015—2020年中法高考试卷,基于6个核心素养的考查比重绘制图2.

图2 核心素养的逐年变化
从图2中不难发现,中国的素养考查以逻辑推理、数学抽象、数学运算、直观想象为主,数据分析与数学建模素养考查比例较低.直观想象素养在2019年考查比例降低,2020年又恢复原有比例.整体来看,各年分布较为稳定,变化不大.法国卷数学抽象、逻辑推理、数学运算考查最多,除2015年数据分析考查比例较高,及2019年数据分析考查比例较低外,其余年份直观想象、数学建模、数据分析素养考查相对均衡.整体来看,逐年稳定性不如中国,波动较大.其中法国Ⅰ卷数学运算素养考查比例高于Ⅱ卷,逻辑推理素养考查低于Ⅱ卷,Ⅰ卷直观想象素养考查比Ⅱ卷更稳定.这与试卷考查内容有关.Ⅰ卷常考查几何相关知识,对直观想象与数学运算素养考查较多.Ⅱ卷则常考查矩阵、数论等知识,对逻辑推理素养的考查较多.相较而言,在数学建模素养上法国考查得更多,且逐年相对稳定,直观想象素养的考查则具有很大的波动性.法国在数据分析素养考查上整体呈现一个下降的趋势,数学抽象则呈现上升趋势.
3.3 基于关联程度的中法核心素养考查对比
为分析中法高考近6年试题核心素养考查的关联程度,对数据进行对应分析.首先,利用Excel将二维表数据转化为一维表,接着完成变量编码,再将数据导入SPSS 22.0进行分析.利用SPSS 22.0中的“降维—对应分析”绘制试卷与核心素养的对应分析联合图.由于涉及数值并非频数,而是比重,模型中所用距离为欧式距离,采用的正态化方法为对称,如图3.
在图3中,SY代表核心素养指标,SJ代表中法各套试卷.从图3可以看出,试卷和核心素养在空间上都区分开了.分维度来看,在核心素养维度上的区分度稍差一些,存在素养分布密集的情况.从试卷上来看,2015年法国Ⅰ卷与2018年法国Ⅱ卷距离原点较远,且互相远离.说明这两套试卷在核心素养考查水平上与平均水平有较大差距,且考查特点有所不同.全国卷2018年与2019年相互靠近,2016年与2017年相互靠近,2020年靠近2015年,相互靠近的试卷的素养考查特点相似,法国试卷有较好区分度.从核心素养考查来看,数学抽象A3,数学建模M3与数据分析D3紧密相关,且M3与D3在同一方向,说明其考查特点相似,差异不明显.从数学角度来看,考查数据分析多为统计类题目,此类题目常基于现实情境考查,需要学生从实际情境中抽象出数学问题,离不开数学抽象与数学建模.直观想象I1与逻辑推理L1相互靠近,从数学角度来看,简单的数形结合问题需要学生熟练掌握应用基本命题、概念,进行简单逻辑思考,从而加以解决.从两维度的联系来看,2020年全国卷与逻辑推理L3距离较近,位于原点同一方向且远离原点,说明二者存在明显关联,O1则在反方向上,说明2020年全国卷对逻辑推理L3的考查水平明显高于其它年份,对数学运算O1的考查则明显较少.另外,法国2016年两套数据与数据分析D3在同一方向上,说明两套试卷对D3考查较多.2015年法国Ⅱ卷与数据分析D1相互靠近,2015年法国Ⅰ卷与该素养在同一方向上,说明2015年法国两套试卷对该素养考查明显高于平均水平.这与原始数据也相吻合.
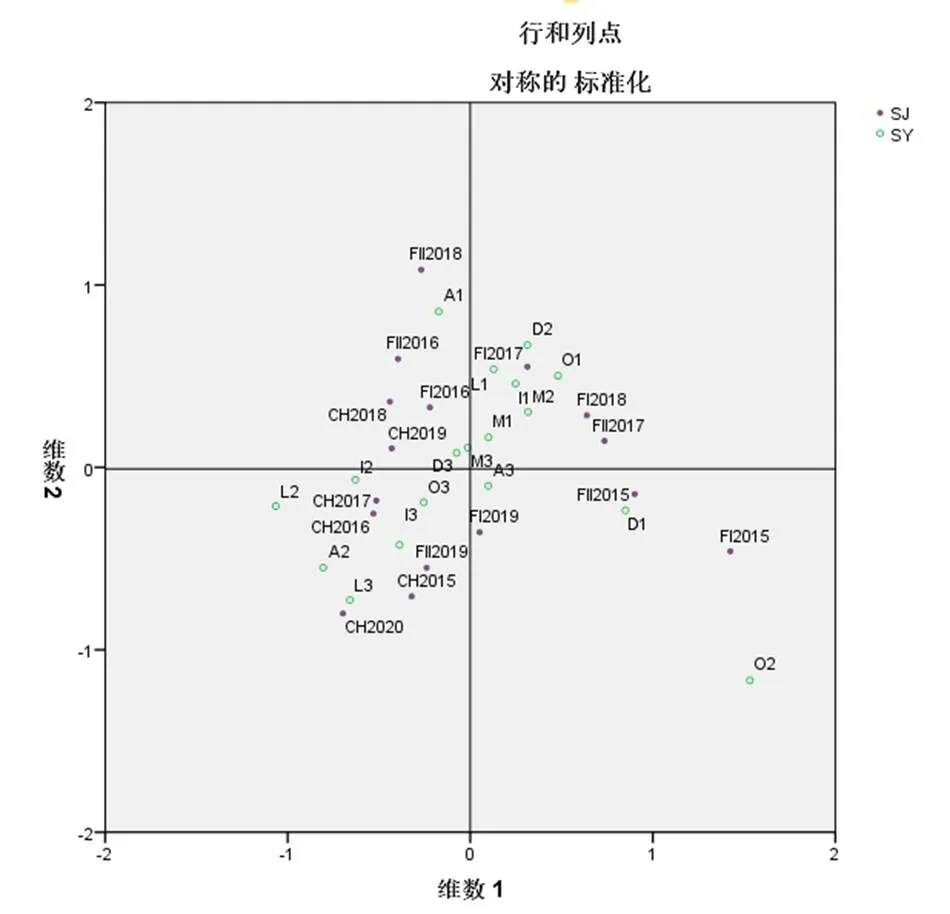
图3 试卷与核心素养的对应分析联合图
3.4 基于受重视程度的中法核心素养考查对比
为分析中法高考试题核心素养的受重视程度情况,针对16套试卷的18个核心素养水平考查比重,采用系统聚类中的平均联接方法对该数据进行变量分类.定义类间的距离平方为这两类变量间的平方欧几里得距离.中国核心素养聚类结果如图4.

图4 中国核心素养聚类图
基于数据指标以及对核心素养考查情况的分析与现实意义解读,确定聚类数为4,具体如下:第一类:M1、D1、D3、M2、D2、M3、I1、A3、L1(均值0.014);第二类:A1、O1、I2、O3、I3(均值0.062);第三类:A2、L3、L2(均值0.119);第四类:O2(均值0.206).根据4类核心素养的均值,可以得出第三类与第四类是中国考查较多的素养.其中,知识迁移水平的数学运算素养考查最多,该水平下的逻辑推理与数学抽象考查也较多.同时,中国对逻辑推理的知识创新水平的考查也较多.
为分析法国高考试题对核心素养的受重视程度,对法国核心素养考查进行聚类分析,具体见图5.

图5 法国核心素养聚类图
同样基于对核心素养考查情况的分析与现实意义解读,确定聚类数为4,具体如下:第一类:I3、D3、M1、M3、A3、O3、L1、M2、I2、I1、D1(均值0.026);第二类:A1、D2、O1、L3、A2(均值0.071);第三类:L2(均值0.111);第四类:O2(均值0.253).计算这4类的均值,发现几类素养所占比例均值逐步上升.其中,第三类(O2)与第四类(L2)是法国卷考查比重较大的素养水平,即逻辑推理的知识创新水平和数学运算的知识迁移水平.
3.5 基于相关程度的中法核心素养考查对比

3.6 基于集中程度的中法核心素养考查对比
为分析中法高考试题对核心素养考查的集中程度,计算中法16套试卷中每道题考查核心素养数目,汇总考查不同素养数的题目比例,如图6.从图6可以看出,全国卷单道题考查3个核心素养、4个核心素养较多,考查5个核心素养的题目也占据一定比例,只考查单个核心素养的题目很少,仅占0.54%.法国则以单道题考查2个、3个、1个核心素养为主,考查3个以上核心素养的题目比例远低于全国卷.
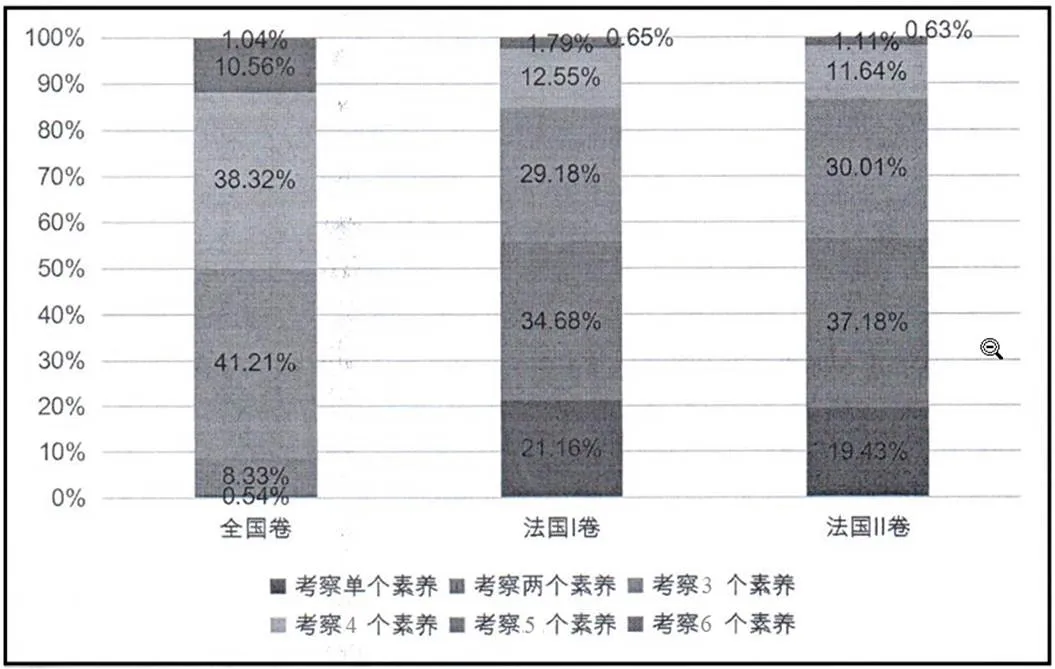
图6 中法试卷每道题考查核心素养数目比例
4 讨论与展望
4.1 拓展中法数学高考研究
现有的法国高考研究多集中于其制度改革,穿插试卷翻译.从高考考题本身出发的研究,主要集中在主题式命题方式分析以及综合难度评价,缺少基于核心素养视角的法国高考考题探究.因此采用核心素养评价方法,对2015—2020年中国理科数学全国Ⅰ卷与法国本土高考理科试卷进行核心素养考查量化分析,借助中法对比的探究方式为高考研究提供了新的视角.
4.2 拓宽试题分析的研究视角
基于核心素养量化数据,利用对应分析、聚类分析、相关分析等多元统计分析方法,进行关于整体分布、逐年变化、关联程度、受重视程度、相关程度、集中程度的中法核心素养考查对比,拓宽了试题分析的研究视角.
4.3 研究的局限与展望
在分值划分时,由于法国试卷只给出了大题分值,故对小题分值采用平均处理的方式,这与实际情况会有一定出入,从而造成误差.同时,李华等人虽然对素养水平的划分已较为详尽,但针对具体试题的素养的分值划分仍会具有一定的主观性.此外,由于法国取消了2020年高考,故在样本上有一定的局限.
5 结论
5.1 中法高考卷在核心素养考查上存在相同点
中法高考卷从整体分布来看,均重视数学运算、逻辑推理与数学抽象的考查,特别地,对于数学建模素养,中法都重视知识迁移水平层面的考查.基于受重视程度分析,可知中法高考题的数学运算素养都达到知识迁移水平,逻辑推理素养都达到知识创新水平.
5.2 中法高考卷在核心素养考查上存在差异性
基于整体分布,发现对数据分析素养考查,中国重视知识迁移水平层面的考查,法国则在此水平基础上增加知识创新水平方面的考查.基于逐年变化,可知近些年来,中国高考卷对六大核心素养考查的分布比例较为稳定,法国试卷的稳定性则不如中国.此外,数学建模、数据分析素养方面的考查,法国卷多于中国卷.基于对应分析,可知中国近5年全国卷数据分布在第二、三象限,总体区分度不大,而法国则不同.基于相关程度分析可知,中国逻辑推理和数学建模显著负相关,而法国逻辑推理与数学运算显著负相关以及数学抽象与数据分析显著负相关.基于集中程度分析,中国高考卷单道题考3~4个核心素养较多,部分题目甚至一次考查5个核心素养,而法国每道题多考查1~3个核心素养,且侧重点更为单一.
6 思考与建议
中国《课标》明确提出六大数学核心素养,高中数学教学理应注重培养学生的数学核心素养.在六大核心素养基础上,高考数学考查的学科素养可以凝练为4类:理性思维、数学应用、数学探索、数学文化.任子朝、赵轩曾提出高考数学学科素养与中国《课标》提出的6个核心素养的关系[17],如图7.《教育部考试中心命题专家解析2020年高考数学试题》中提到,试题命题应重视数学本质,突出理性思维、数学应用、数学探索、数学文化的引领作用[18].因此,基于高考数学学科素养,提出关于高考命题的思考以及建议.
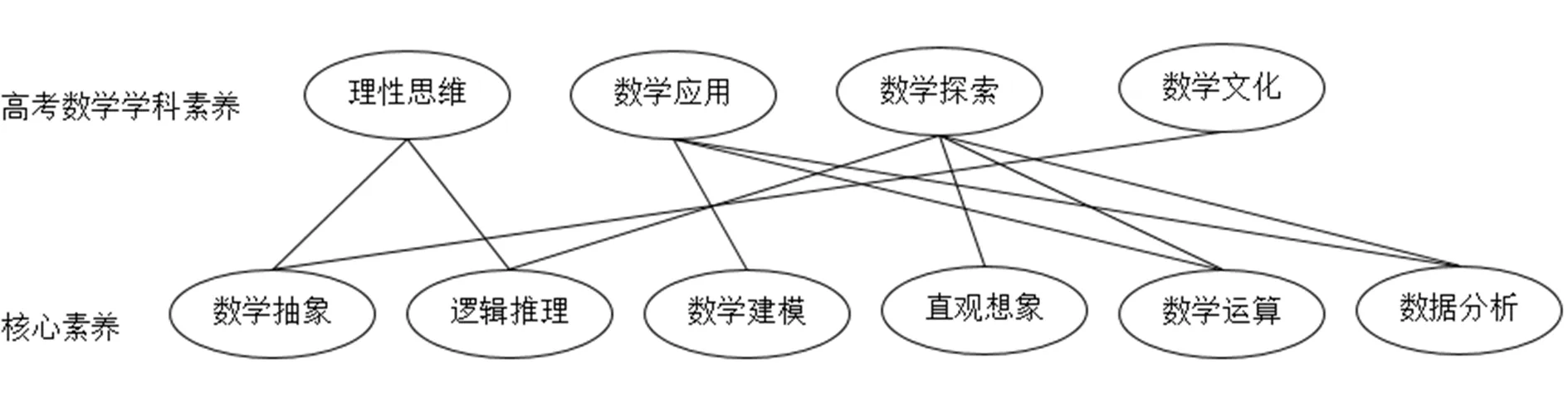
图7 高考数学学科素养与核心素养关系
6.1 注重理性思维 体现逻辑性
理性思维的考查涵盖数学抽象与逻辑推理两个核心素养,它们两个也是高考卷主要考查的对象.从中法试卷的对比分析中可以发现,在核心素养考查方面,中国注重数学抽象与逻辑推理的考查,且较稳定.法国Ⅰ卷逻辑推理素养考查低于Ⅱ卷,对数学抽象的考查整体上呈现上升趋势.由此可见,中法高考都重视对理性思维的考查,充分体现数学的两个基本特征——抽象性和逻辑严密性.
理性思维在学科素养中起着最本质的作用.高考数学通过考查学生的理性思维,判断学生的数学能力,考查学生的推理判断和抽象数学问题的能力.高考对理性思维的重视有利于教师在教学活动中重视学生理性思维的培养.理性思维的培养有利于学生思维能力、推理能力、创新能力的提高.有利于培养学生由未知的数学问题推理出新内容的能力,同时提高学生解决数学问题的能力.综上,在高考命题中一定要保持对理性思维的重视以及考查.
6.2 强化数学应用 体现实践性
数学应用的考查涵盖数学建模、数学运算、数据分析3个核心素养.试题在考查数学建模的时候大多需要对数学模型进行数据分析,同时也离不开数学运算.中国全国卷核心素养考查以直观想象为主,数学建模与数据分析少,而法国对这3项的考查相当.中国涉及数学建模素养的题目多偏重于考查学生对建模情境的理解.近些年来,全国卷建模题型的数量和分值有所增加与改善,对数学应用的考查有所增加,体现实践性.
中国《课标》专门设置了建模专题,训练学生依据题目信息,利用数学知识,建立数学模型,再进行运算,最后解决问题.利于培养学生的应用意识,强化学生的数学应用素养.在高考命题中,数学应用的强化可以从以下几方面入手:(1)设置创新情境,注重开放性.利用创新性情境设计数学问题,学生在解决问题的过程中需要开放思维,对创新性情境进行深入分析,方可获取关键信息和数据,可以据此考查数学建模、数据分析以及数学运算素养,学生在此过程中能充分感受到数学的应用价值.(2)均衡考查难度,控制运算量.中法高考题均对数学运算考查较多.数学运算素养重视考查学生的运算能力、运算方法、运算思维,高考数学离不开对数学运算的考查,但在命题时要考虑到运算量以及难易程度,避免难度过大.
6.3 加强数学探索 体现过程性
数学探索素养考查涵盖逻辑推理、直观想象、数学运算、数据分析4个核心素养,考查学生利用观察、想象、分析、推理创造性地运用数学知识解决数学问题,体现过程性.通过比较分析发现,中国对数学运算、逻辑推理素养考查较多,近年来法国关于数学运算、逻辑推理素养的考查相对均衡.但命题时中国更加注重直观想象素养考查,法国则更加注重数据分析的考查.
由于数学探索包含4个核心素养,在命题中需要注意合理设置每道题的核心素养个数及其考查水平,具体如下:(1)调控核心素养考查个数,突出试题综合性.《2019年普通高等学校招生全国统一考试大纲——理科数学》中提出要突出高考命题的综合性要求[19].在考查数学探索素养命题时,一道题可考查多个核心素养,有利于人才的全面培养,可以帮助培养学生的分析总结能力.但在命题时要调控每道题考查核心素养个数,中国高考卷单道题考查3个、4个核心素养的较多,而且有时候会考查5个核心素养,这无疑给学生学习带来挑战,建议根据核心素养间的关联性(如基于试卷分析可见,直观想象与逻辑推理相关性较高),在命题时合理选择核心素养.(2)均衡核心素养考查水平,突出试题合理性.课程设计中各个核心素养的分布本身是不均匀的.多个知识点以及多个素养考查有利于培养学生融会贯通能力,但在命题中也要考虑到高中学生的认知与分析能力,均衡核心素养考查水平,避免一道题目考查多个核心素养时过难,增加学生负担.比如,在命题中若考查运算素养的水平高,可以适当降低对逻辑推理考查的要求.综上,在考查数学探索素养时,注意调控单道题核心素养考查个数,并均衡多个核心素养的考查水平(如基于整体分布可见,数据分析素养中国考查较少,命题时可考虑适当调整素养考查水平),有利于合理考查数学探索素养,提高试题命制水平.
6.4 关注数学文化 体现育人性
数学文化的考查以数学抽象为主.中法高考题对数学抽象考查较多,且以知识迁移水平为主.但中国试题在数学历史以及科学等数学文化方面的结合不如法国试题.近些年来,中国试题与数学文化背景结合情况有所改善,渗透数学文化与审美,如2019年试题中出现“断臂维纳斯”,2020年试题中出现“埃及胡夫金字塔”,由此可见,中国对试题与数学文化方面的结合有所重视并有所改变,体现育人性.
《国务院办公厅关于新时代推进普通高中育人方式改革的指导意见》提出,在高等学校招生全国统一考试命题中要加强情境设计,培养学生审美能力和文化理解素养[2].中国《课标》提出了数学的美学价值,数学文化的融入有利于培养学生的数学审美能力[4].而且数学文化的推广有利于帮助学生学会运用数学学科知识解决生活中的问题,提高解决实际问题的能力,进而提升实际操作能力.在高考命题中,数学文化的推广可以从以下几个方面入手:(1)借助传统文化.如在数学题目中借助古桥“赵州桥”、古建筑“天坛”以及数学史中著名问题“折竹抵地”“七桥问题”等考查学生数学知识.将优秀的历史传统文化融入题目之中,一方面可以提高学生的学习兴趣,另一方面有利于培养学生的文化自豪感.(2)借助中外数学家的故事,如高斯、阿基米德、华罗庚等,在解决数学问题的同时,体会故事背后的育人价值.(3)借助优美图形,如平面图形心形线,螺旋线等以及优美的立体图形.在命题时结合优美的曲线图形,引导学生感受数学之美.
[1] 国务院.国务院关于深化考试招生制度改革的实施意见[J].人民教育,2014(18):16–19.
[2] 国务院办公厅.国务院办公厅关于新时代推进普通高中育人方式改革的指导意见[J].人民教育,2019(Z2):10–13.
[3] 中华人民共和国教育部.关于全面深化课程改革落实立德树人根本任务的意见[EB/OL].(2014–03–30)[2019– 11–12].http://www.jswxedu.com/html/jyfw/zgzj/190.html.
[4] 中华人民共和国教育部.普通高中数学课程教育标准(2017年版)[M].北京:人民教育出版社,2018:10.
[5] 教育部考试中心.中国高考评价体系[M].北京:人民教育出版社,2020:20–21.
[6] 张玉环,吴立宝,曹一鸣.法国初中数学教材特点剖析及启示[J].数学教育学报,2016,25(6):32–37.
[7] 龚妙昆.2007年法国高中毕业会考(暨高等学校入学考)数学试题[J].数学教学,2008(11):46.
[8] 胡凤娟.主题式命题:来自法国数学高考试题的启示[J].中学数学教学参考,2019(25):74–78.
[9] 张玉环,周侠.综合难度视角下中法高考数学试题的比较研究——基于2015—2019年中国和法国高考数学试卷[J].数学教育学报,2020,29(3):43–50.
[10] Ministère de l'Éducation nationale et de la Jeunesse. Programme de mathématiques de seconde générale et technologique [EB/OL]. (2019–07–25) [2019–08–20]. https://cache.media.education.gouv.fr/file/SP1-MEN-22-1-2019 /95/7/spe631_annexe_1062957.pdf.
[11] 喻平.数学核心素养评价的一个框架[J].数学教育学报,2017,26(2):19–23.
[12] 李作滨.素养导向的数学测评研究——以2018年高考为例[J].数学教育学报,2018,27(6):33–37.
[13] 俞梦飞,章飞.核心素养视角下数学高考试卷评价研究——以2018和2019年江苏高考卷为例[J].数学教育学报,2020,29(2):35–40.
[14] 李华,胡典顺.基于数学核心素养评价框架的试卷测评研究——以2019年高考全国卷为例[J].数学教育学报,2020,29(2):18–23.
[15] 凡桑.法国2020年高考新规出炉[N].欧洲时报,2020–06–26(1).
[16] Ministère de l’Education Nationale. Baccalauréat général session 2015—2019 mathématiques series [EB/OL]. (2019–07–01) [2020–02–10]. https://www.education.gouv.fr/examens-et-diplomes-41459.
[17] 任子朝,赵轩.基于高考评价体系的数学科考试内容改革实施途径[J].中国考试,2019(12):29–30.
[18] 王家源,林焕新,赵秀红.教育部考试中心命题专家解析2020年高考数学试题[N].中国教育报,2020–07–08(4).
[19] 教育部考试中心.2019年普通高等学校招生全国统一考试大纲——理科数学[EB/OL].(2019–01–31)[2020–02 –19].http://gaokao.neea.edu.cn/html1/report/19012/5965-1.html.
A Survey of the Junior High School Students’ Logical Reasoning Abilities
YAN Qing1, YU Ping2
(1. Faculty of Mathematics and Statistics, Hubei University, Hubei Wuhan 430062, China; 2. School of Mathematical Sciences, Nanjing Normal University, Jiangsu Nanjing 210046, China)
Based on a survey of the logical reasoning ability of junior high school students in China, which mainly focused on the differences between grades and schools as well as gender differences, we came to the following conclusions. First, students in China mostly have a basic understanding of logical reasoning; this ability depends on their understanding of both logical forms and mathematical knowledge. The ability develops fast during the period of junior high school, especially along the dimension of modus ponens. Furthermore, the ability of students in key schools is superior to that of students in normal school, and the difference between the two types of schools doesn’t change much with age. Finally, there is no significant difference in the ability of boys versus girls, although the boys have greater variability than the girls.
mathematics key competencies; logical reasoning; difference between schools; gender difference
G40–059.9
A
1004–9894(2021)01–0042–07
张玉环,周侠,陈爽.核心素养视角下中法高考数学试题的比较研究——基于2015—2020年中国和法国高考数学试卷[J].数学教育学报,2021,30(1):42-48.
2020–10–20
2018年河南省教师教育课程改革研究项目——提升学生数学核心素养的研究与教学实践(2018-JSJYZD-006);河南大学研究生教育创新与质量提升计划2019年项目——学科教学(数学)教学案例库建设和实践(SYL19040113);河南大学2019年度本科教育教学改革研究与实践项目——数学师范类课程线上线下混合式教学的实践与研究(HDXJJG2019-20)
张玉环(1983—),女,河南商丘人,副教授,博士,硕士生导师,主要从事数学教育、教师教育研究.
[责任编校:陈隽、张楠]
