基于“问题提出”的小学数学教师主题式专业发展：理论建构与实践探索

宋乃庆，张莎莎，陈 婷，李忠如，蔡金法，

基于“问题提出”的小学数学教师主题式专业发展：理论建构与实践探索

宋乃庆1，张莎莎1，陈 婷2，李忠如3，蔡金法4，1

（1．西南大学 数学与统计学院，重庆 400715；2．西南大学 教育学部，重庆 400715；3．西南大学 教师教育学院，重庆 400715；4．美国特拉华大学 数学系，纽瓦克 19716）

随着学校对数学问题提出的日益重视，教师学习运用问题提出进行教学成为迫切需要．建构基于“问题提出”的主题式教师专业发展的相关理论．基于“问题提出”的主题式教师专业发展具有两层含义：一是运用问题提出进行教学，二是聚焦于教师专业学习的内容．通过系列小学数学问题提出教学工作坊，探讨实施小学数学教师学习“问题提出”教学的主题式教师专业发展的初步尝试，介绍了工作坊中教师对问题提出的理解和通过问题提出进行教学的感知效果的初步研究结果．

问题提出；主题式教师专业学习；小学数学；教师专业发展

1 问题提出

爱因斯坦曾言，“提出一个问题往往比解决一个问题更重要”[1]，提出问题的巨大价值由此可见一斑．无论在阅读研究还是数学教育研究领域，问题提出长期被认为是至关重要的智力活动[2–3]，具有实现学习机会的公平化与最大化，促进和反观学生知识理解，提高学生问题解决能力，激发学生创造力和促进学生非认知能力发展的教育价值[4]．近年来，随着创新能力在世界范围内受重视程度的提高，问题提出作为创新思维的着力点越发受到世界各国的关注，将问题提出纳入学校教育的议题已经逐渐成为各国不同学科课程和教学改革关注的焦点之一．例如，全美数学教师委员会NCTM颁布的系列数学课程文件中均强调要给学生提出问题的机会[5–7]，日本文部科学省颁布的文件也有相关论述[8]．中国《义务教育数学课程标准（2011年版）》的总目标将原有的“两能”拓展到“四能”，并指出教师应将问题提出整合到课堂教学之中，增加“问题提出教学活动”[9]．然而，尽管数学问题提出在上述“计划课程”中被寄予了很高的期望，但在教材编写和实际教学中并未得到同等地位的重视，教材中问题提出活动的类型较为单一、占比极低[10–11]，导致教师将问题提出整合到课堂教学活动中面临着巨大挑战，进而制约了学生数学问题提出能力的发展．

教师作为基础教育改革发展中最重要的有生力量，其自身问题提出能力及问题提出教学经验是培养学生问题提出能力的重要前提．目前，数学教育领域对如何帮助教师成为更好的问题提出者以及如何帮助他们学会运用问题提出开展教学知之甚少[12]．同时，问题提出作为一种不太“常规”的教学手段或教学目标，转变教师固有的教学信念与教学方式并非一日之功．因此，如何精心设计有效的问题提出教师专业发展活动成为关键所在．

教师培训是加强教师队伍建设和提高广大教师专业能力的有效途径，长期受到国家的高度重视．自2010年国培计划实施以来，截至2019年，中央财政累计投入国培计划专项经费157.84亿元，培训中小学幼儿园教师超过1 500万人次，培训管理效度明显提高，培训模式不断更新，培训质量明显提升[13]．然而，参训教师主体性缺失，使得相当一部分教师仍处于“被动接受”状态．与此同时，被教师广为诟病的教师培训重理论、轻实践的痼疾依然存在，不少教师参与培训后感到很难将所学到的知识和技能运用到日常课堂教学之中．因此，这里尝试用主题式培训这种新的教师培训方式，以期更好地促进教师的专业发展．

主题式培训关注培训内容间的历史生态关联，其主题形式（多次培训活动体现一个主题思想）能使教师明确这一阶段要获得哪些方面的提升，而且在实现阶段性成长之后，下一阶段的主题应在前一主题基础上的稳步提升，有利于整体设计培训内容的难度和进程，支持教师在贯彻落实理念的同时不断加强自我效能感，从而提高教师对自我专业发展的热情[14]．因此，这里以有效教师专业发展的先进成果为基础，尝试创新教师培训方式——基于“问题提出”的主题式教师专业发展，并在小学数学“问题提出”教学工作坊中进行实践．这里将简析基于“问题提出”的主题式教师专业发展的相关概念和理论基础，并结合小学数学“问题提出”工作坊，介绍其实施过程与效果，助推问题提出教学落地．

2 基于“问题提出”的主题式教师专业发展的 相关理论

2.1 概念界定

2.1.1 问题提出教学

数学问题提出教学法最早出现在波利亚于1945年所著的《怎样解题》一书中．然而20世纪80年代之前，相对于问题解决，问题提出一直是个被忽略的研究领域．“问题提出”最为直接的含义是指基于特定的问题情境形成并表达问题的认知过程[15]．其既可以作为一种独立的认知活动；又可以作为一种教学目标，即促进学生问题提出能力的发展；还可以成为一种教学手段，即通过问题提出进行教学[16]．问题提出教学是指围绕教学目标，教师依据课程材料中的教学任务，设置问题提出的情境，师生通过课堂互动共同参与问题提出的过程，以达成教学目标的教学．这里所指的问题提出教学是以学生问题提出为主的课堂教学，以学生所提问题为驱动，教师作为辅助角色引导教学以达成教学目标．

2.1.2 主题式教师专业发展

“主题”既能体现社会对教师的要求，又蕴涵于教师自身需要的各种教育问题，可以是所有教师群体都面临或关心的问题，也可以是学科教育所特有的问题[17]．主题式教师专业发展模式是以主题目标和具体目标为前提，围绕主题来设置课程内容，组合专业引领、案例分析、情境模拟、问题导向等方式的一种培训模式，具有聚合性、主体参与性、合作性和集约性的特点[18]．它具有明确的目标和计划，主要通过培训内容和培训方式来体现培训主题，实现培训目标，提高培训效果[19]．

基于“问题提出”的主题式教师专业发展是指以问题提出教学为主题，通过专家引领、案例学习、课堂观摩等多种形式，帮助教师获得问题提出教学知识，树立问题提出教学信念以及提升教师问题提出教学能力的教师专业发展模式．

2.2 相关理论

2.2.1 教师专业发展的一般路径

教师专业发展的意义和价值不仅在于自身职业生命质量的提高，更在于它是促进学生发展的必要条件．但教师学习并不是直接对学生的学习产生影响，而是通过教师课堂教学行为的改变来实现学生学习的提高[20]，教师教学行为的改变则依赖于教师通过学习所引起的自身知识和信念的改变来达成．即，教师专业发展遵循的一般路径[21]，其基本假设是：教师通过学习，促进知识的增长和信念的改变，进而改变教师课堂教学行为，以提高学生的学习能力．如前所述，问题提出教学在中国课堂实践中仍面临巨大挑战，因此，教师需要通过教师专业发展活动掌握问题提出教学知识并改变原有教学信念以转变教学行为．

图1 教师专业发展的一般路径

2.2.2 有效教师专业发展活动的特征

高效的、能够对教师教学实践和学生学习产生积极影响的教师培训活动具有如下5个特征[22]：内容聚焦；基于学生的学习和思维；密切联系教学实践；建立学习共同体；培训时间的持续性．

内容聚焦．内容聚焦指教师专业发展活动聚焦于改善或深化教师的数学（科学等）内容知识．教师培训的内容应该聚焦于具体的学科内容，而不是抽象的教育原则和教学方法．研究表明，内容聚焦的教师专业发展活动有利于教师教学和学生学习成就的提高[23]，特别是概念理解，教师专业发展活动聚焦于主题或学生的学习将是改变教学实践相当重要的因素[24]．

基于学生的学习和思维．多项关于教师专业发展的文献研究都揭示出一个明确且具有一致性的结果：关注学生的学习和思维的教师专业发展活动往往更加有效[25]．引导教师能够站在学生角度定义他们将要学习的概念和技能，并且能识别出可能对学生造成学习障碍的内容，这样的教师专业发展活动可以改善教师教学实践及学生的学习结果[26]．

密切联系教学实践．国际教师教育学倡导教师学习的三大定律，即越是扎根教师的内在需求越是有效；越是扎根教师的鲜活经验越是有效；越是扎根教师的实践反思越是有效[27]．如果教师专业发展活动应用与教师进行教学设计和课堂教学直接相关的知识，将对教师的教学实践产生积极的影响，从而促进学生学习的提高[28]．教师们判断培训是否具有价值的依据是它是否为教师提供了“实际动手操作”任务的机会，改进教师知识和教学方法[29]．

建立学习共同体．教师学习共同体是教师基于共同的目标以及对所属团体的归属感组织起来的学习团体．教师学习共同体可以从一定程度上促进教师学习共同体内部成员的深度交流，有利于激发教师专业自主发展的主体性，挖掘和共享教师群体的资源，提高教师的实践智慧，培养教师的合作意识和团队精神．建立教师学习共同体可以使教师知识得以加深，能力得以增强，教学得以改善[30]．

培训时间持续．培训时间的持续不仅包括参训教师参与活动所花费的时间，也包括培训活动跨越的时间周期．有研究发现，若教师专业发展活动每年为教师提供49小时的学习时间，学生的学习可以提高将近21%[23]；教师在接受80个小时甚至更多时间的专业培训后，相对于学习时间较少的教师而言，更愿意将所学到的教学策略应用于教学实践[28]．

2.2.3 教师学习的情境视角和“改进科学”的视角

情境学习理论认为，学习不仅仅是个体性的意义建构的心理过程，更是社会性、实践性的参与过程．学习者最好基于情境性的活动来习得知识，当学习者处于实际情境中时，其所获取的知识往往是一种默会的知识[31]．基于情境视角的研究表明，促进教师专业发展和帮助教师克服困难有两个关键方面：第一，为教师专业发展提供情境支持；第二，培养教师专业发展认同感，即教师在情境支持下改变他们的教学，克服心理障碍以及确定新的教学方法[32]．从这一角度来看，为教师的情境学习提供支持是基础．此外，教师还需要具有不同知识、技能的研究者在其职业生涯的不同时期给予支持和帮助[33]．长期、紧密联系的教师与研究者的合作伙伴关系可以将双方独特的专业知识结合起来，使得每一方在提升学生学习这一共同目标时发挥同等作用[10]．

“改进科学”的方法聚焦于利用从情境中获得证据从而解决参与者在该现实情境中所发现的问题．“改进科学”关注六大问题．第一，聚焦要解决的具体问题是什么？问题越具体、确切，越容易被解决．第二，变量是核心问题，由于特定的情境因素，变量会发生变化．第三，查看产生当前结果的系统，理解造成差异性结果的不同制度的运行机制．第四，需要采用怎么样的测评工具去评估取得的进步和改善后的效果．第五，改进源于计划—执行—学习—行动（PDSA）这一循环过程来促进快速、高效地学习，从而取得进步．第六，以共同发展为导向，即在共同体内吸引关键参与者[34–35]．基于此，它可以帮助理解教师设计、实施、修改和再设计教学方案以改进课堂教学的循环过程．

3 基于“问题提出”的主题式教师专业发展的实践

小学数学“问题提出”教学工作坊是基于“问题提出”的主题式教师专业发展在小学数学学科内容下的实践，在过去两年中，成功开展了4期，下面将说明工作坊的实施特点．

（1）培训主题聚焦，从提出问题到课堂教学实践．

“主题式”是指基于具体内容的数学问题提出教学的专业发展模式．具体地说，4期小学数学“问题提出”教学工作坊均聚焦于同一主题——“问题提出”教学，依托小学数学五年级《简易方程》单元内容，从教师提出数学问题到运用问题提出进行数学课堂教学，构建理论通往实践的专题链．具体而言，第一期工作坊围绕“如何帮助小学数学教师成为好的问题提出者”来展开，侧重于对“问题提出”本质、价值的概述，帮助教师提出问题以及观摩问题提出教学案例，并初步尝试《简易方程》单元中某课时问题提出教学设计；第二期工作坊以“如何将问题提出运用于课堂教学中”为主旨，学员在聆听专家对问题提出开展的课题研究与教学改进历程后，坚定问题提出教学的信念，修改《简易方程》教学设计，在实际课堂中尝试问题提出教学；第三期工作坊则致力于“问题提出数学教学课例研讨”，通过课例展示、说课、观摩、研讨等形式，学习将问题提出运用于数学课堂教学中的方法并反思自身课堂实践，再次修改前次教学设计；第四期工作坊以“问题提出《简易方程》单元教学设计”为主要内容，专家、教师与工作坊学员分别借助课堂实录分享问题提出教学实践经验．从理念渗透到课堂实际操作始终围绕同一主题同一教学单元内容，使得学员对问题提出概念的理解越发清晰，增强对问题提出教学理念的认同感，树立用问题提出进行课堂教学的信念，并有效转化为课堂教学实践．

（2）活动设计基于学生的学习和思维，提升教师问题提出课堂教学．

教师专业发展以促进学生的学习发展为最终落脚点，因此，在对教师进行培训时理应将学生作为重要的隐形对象考虑在内．教师对学生的了解程度越高，其提供给学生的学习机会越多[25]．如前所述，问题提出教学较为倡导的方式是以学生所提问题为驱动，教师作为辅助引导教学目标的达成．因此，教师运用问题提出进行教学，除自身具备问题提出能力，更为重要的是预设学生可能提出的问题．工作坊设计了不同的问题提出任务，在培训的不同阶段向学员发放不同的问题提出任务，不仅要求教师自己根据已有情境或给定表达式提出问题，而且要求教师站在学生的角度，预测学生可能会提出的问题，并对学生提出问题的类型、难度等进行预设．如，要求教师根据现实情境“佳佳、沙沙和小斌开车一起回家，佳佳比沙沙少开150公里，沙沙开的公里数是小斌的12倍，小斌开了50公里”，尽可能多地预测学生可能提出的问题．又如，根据表达式“6+5=25”尽可能多地预测学生能提出用该算式解答的数学问题．研究发现，教师能够预测出学生可能提出的不同难度的问题，如“沙沙开了多少公里？”“佳佳开的公里数是小斌的多少倍？”“如果每人最多开100公里就需要更换另一个人开，他们开完全程至少要换多少次？”．教师能够根据数学表达式编出情境多样的数学问题，除纯数学情境（比一个数的6倍多5的数是25，这个数是多少？）外，教师最常选用的是工程、行程以及购物情境，如“妈妈买了一些水果，买的梨子是苹果的6倍多5千克，梨子一共25千克，苹果有多少千克？”，其它选用的情境还有测量、家庭、学校情境等[12]．这一过程为教师识别可能造成学生问题提出障碍的内容提供机会，增强教师对学生思维发展状况的了解，从而能够在课堂教学中为不同需求的学生提供不同的学习机会，最终达成教学目标．

（3）培训活动密切联系教师教学实践，为教师学习提供情境支持．

教师的专业发展须同学校教学改革的实践，特别是课堂改革的实践紧紧挂起钩来，否则其所谓的专业发展是不靠谱的[36]．工作坊的培训活动形式多样，将教师喜欢的案例学习、课堂观摩等作为主要培训方式，密切联系教师的教学实践，在真实情境中发展教师的问题提出知识、信念，转变课堂教学．工作坊为提升教师问题提出能力所创设的问题提出任务情境，一部分来自先前研究，一部分则通过对现行小学数学教科书中问题的改编而成，从教师最为熟悉的日常教学材料入手，拉近教师与问题提出之间的距离，同时让教师学习如何将教科书中现有的教学任务修改为问题提出的任务．以往的教师培训中，教师最为关心的问题是“如何做”，因此，应该将教师的学习与教学实践充分结合．案例学习被认为是一种较好的策略，它为学习者提供了在类似真实情境中学习教学的经验，尤其是为学习者呈现出了真实教学的复杂性[37]．工作坊为教师学习问题提出教学提供了丰富的案例，由课例的执教者现场说课，详细讲述自己如何运用问题提出成功教授了一年级的两位数加、减法的复习课；学员观摩运用问题提出教授的四年级乘法分配律新授课实录等．为创设真实教学情境，工作坊以小学作为主要培训场所，采用借班上课、同课异构的形式，直接感受常规课与运用问题提出授课的差异．将教师置于真实的教学情境中，更有利于教师克服理论到实践转换的困难，将知识内化为自己的经验，从而改进教学．

（4）以共同发展为导向，建立教师学习共同体．

在每期问题提出教学工作坊报名之初，要求每位教师撰写并提交两个关于《简易方程》单元内容的教学设计．通过专家讲解答疑及经验教师的案例展示，教师对问题提出的概念、相关研究及如何在课堂教学中落实有了初步了解．以共同发展为导向，在工作坊开展过程中，给予学员们充分的机会，让每个人都参与提出问题的过程，并分享他们在此过程中的困惑，与培训专家平等对话、交流，加深对问题提出的认识．在理论学习以及课堂实践观摩的基础上组建学习共同体，吸引关键参与者，7~8人为一组，共同对提交的两个教学设计进行研讨、修改，每组由2名研究生负责对该小组的讨论进行组织、记录并辅助，同时培训导师在教师的观念和行动上给予专业支持和帮助．学员在教师学习共同体中进行切磋式、创造性学习，同侪互助、协作，梳理提炼对问题提出的理解及在教学实践中的渗透形式，积极发表看法，尽可能将问题提出的元素在他们认为恰当、合适的地方整合于现有的教学设计中．工作坊结束时，各小组分别展示修改成果，每组有大约10分钟的时间与所有工作坊的参与者分享他们关于问题提出教学设计整合中的问题、经验．之后学员们将修改后的教学设计上交，专家对修改后的教学设计进行分析，既可看出学员培训前后的变化，了解培训效果，又可发现问题，并在下一次培训时反馈给每位学员．建立学习共同体为教师的深度学习、交流、思考提供了充分的机会，对促进学员的共同发展具有重要的潜在意义．

（5）培训时间具有持续性，使教师逐步改进教学行为．

目前工作坊已成功开展了4期，每期历时3天，每半天安排一个学习环节，保证了每期教师学习的时间都在20小时以上．因此，无论是每期工作坊所花费的时间，还是整个工作坊跨越的周期，都保证了培训时间的持续性．如在第一期工作坊的3天时间内，首先对问题提出作概述性介绍，包括问题提出的内涵、重要性及其对促进学生理解和数学学习的重要意义；然后让学员们根据给定的情境按要求自己提出问题；紧密衔接的是要求教师预测学生可能提出的问题；接着要求教师修改关于《简易方程》的教学设计，将问题提出元素融入教学设计中；最后组织教师们讨论有关问题提出的课例．如此联系紧密、环环相扣、持续时间较长的活动为教师对内容、设想及错误想法进行深度讨论提供了更多机会．此外，整个工作坊跨越周期较长，多期连续举办．在前一期工作坊结束后，教师根据培训收获将问题提出应用于实际教学，在试教过程中发现问题，并在后一期工作坊开展之时进行反馈、分享，与同伴进行交流，再由培训专家进行点拨、指导，进而再次修改、完善并在实践中尝试．这样设计、实施、修改和再设计循环，持续的活动能够促进教师快速、高效地学习，不断丰富教师问题提出教学知识，更加坚定运用问题提出教学的信念，为教师在课堂中尝试进行问题提出教学提供了更多机会，对教师的教学实践大有裨益．

4 小学数学“问题提出”教学工作坊的现实成效

教师培训评价作为教师培训工作的“监控器”，是提升教师培训质量的重要保障[38]．教师培训评价应包括两方面的内容：对培训本身的评价和对参训教师的评价．基于小学数学“问题提出”教学工作坊的目的——帮助小学数学教师成为好的问题提出者，树立问题提出教学的信念，并将问题提出成功运用于小学数学课堂，因此，这里将从对工作坊本身的评价以及参训教师问题提出知识、问题提出教学信念、教学行为的转变来考察工作坊的培训效果．

4.1 对工作坊本身的评价

前3期工作坊均设计了“小学数学‘问题提出’教学工作坊培训效果调查问卷”．其中，第一期和第三期涉及教师满意度的调查，包含以下3个客观题：您对本次工作坊的满意程度；本次工作坊在多大程度上达到了您的期望；未来几年中，我们将进一步开展此类“问题提出”的活动，您是否还愿意继续参加．第二期则采用简答题的形式，了解工作坊与以往教师培训的不同之处、独特之处以及学员对工作坊的喜欢和不喜欢的方面．有关第一期工作坊的实施效果在另文中有详细报告[39]，这里仅报告其主要结果．

第二期工作坊共收回有效问卷43份．对教师而言，这是他们第一次参加仅围绕问题提出主题而开展的工作坊，他们认为工作坊的培训内容非常聚焦也很有意义．具体而言，有超过90%的教师认为该次教师培训活动与以往的教师培训完全不相同或不相同，有7%的教师认为差不多，仅有2%认为相同．此外，要求教师列举问题提出工作坊的3个独特之处，29%的教师认为研讨氛围宽松愉悦，可以畅所欲言，深度互动，及时答疑，学员参与度高；26%的教师认为培训形式多样，理论与实践密切结合，活动丰富；24%的教师认为培训密切联系教学实践，深入课堂，案例鲜活，更贴近一线教师的教学实际；14%的教师表示他们在此次活动中收获了新的教学理念．此外，有4%的教师认为培训主题新颖且明确、聚焦，2%的教师认为多次修改同一教学设计，更为深入．在了解参训教师对于工作坊的喜欢和不喜欢之处，每位老师都提及喜欢的方面，涉及案例生动鲜活、理论与实践完美结合、专家及时答疑解惑等众多方面．仅有13位老师提出不喜欢的方面．其中，不喜欢的理由主要是培训时间与教师日常工作时间部分重叠．

由于部分学员数据缺失，为保证数据的完整性，在第一期工作坊中，随机抽取50名学员作为研究样本，第三期保留37个有效样本．两期均有超过90%的参训教师对该期问题提出工作坊感到满意或非常满意．对他们来说，这是最早接触的在一段时间内专注于问题提出的教师专业发展机会，大多数教师（超过60%）认为该次工作坊达到了他们的期望，由于这些积极的体验，第一期50名教师和第三期37名教师均表示非常希望继续参加后续的问题提出工作坊，第三期详细数据见表1．

4.2 对参训教师的评价

4.2.1 教师问题提出知识的变化

第一期工作坊前后，教师对问题提出的认识变化具有统计学意义[39]．对“问题提出”工作坊持不同态度的教师群体，无论是消极组还是积极组，他们从参加1天、2天到3天的工作坊之后，提出恰当问题的数量、问题的难度以及不同难度种类的问题数量都有增长[12]．由此说明，问题提出工作坊有助于提升教师的问题提出能力．

三、四期参训教师的问题提出知识发生了显著变化．以第三期数据为例，如表2所示，工作坊前后教师对问题提出的熟悉程度有显著变化[2(2,= 74) = 29.23,< 0.000 1]，即参加培训后，更多的教师对问题提出更为熟悉．事实上，超过50%的教师感觉对数学问题提出的理解非常好或者说得到了很大的延伸，但是在培训之前，只有3名教师有这样的感受．相对于参加培训之前，37名教师中，超过90%认为参加培训后他们对问题提出更为了解．

表1 对第三期工作坊本身的评价

表2 第三期工作坊中教师对问题提出的了解程度

注：对于卡方检验，由于有某个数据为0，将“完全不熟悉”和“熟悉一点”结合起来；类似地，将“熟悉”和“非常熟悉”结合起来．

在调查教师培训前的问题提出教学经历时，只有约8%的教师有丰富的问题提出教学经历，绝大多数教师在参加问题提出工作坊之前有一点或完全没有运用问题提出教数学的经历．工作坊结束后，调查了教师把问题提出融入课堂教学的意愿程度（1. 非常不愿意；2. 不愿意；3. 中立；4. 愿意；5. 非常愿意）．有将近一半的教师非常愿意将问题提出整合到课堂教学中，并且另外一半教师也愿意将问题提出整合到课堂教学中．

4.2.2 教师问题提出教学信念的转变

第一期工作坊前后，教师对问题提出教学的把握程度发生了显著变化[39]．表3呈现了第三期工作坊培训前后教师用问题提出进行数学教学的把握程度．培训后，教师将问题提出用于数学教学更有把握[2(2,= 74) = 20.86,< 0.000 1]．具体来说，有超过40%的教师对问题提出教学有把握或非常有把握，然而在培训之前仅有8%．此外，相比于培训之前，超过90%的教师对问题提出用于教学更有把握，有一点把握和没把握的教师人数从开展工作坊前减少了近80%．

此外，在四期工作坊结束后的一个学期期末，对学员进行半结构化访谈．从教师对问题提出的信念、驾驭问题提出教学的信念、学生问题提出数学学习的信念3个维度了解其问题提出教学信念．研究结果发现，工作坊对教师问题提出的教学信念总体产生积极影响，工作坊是在教师建立“问题提出的信念”的基础上，对教师“驾驭问题提出教学的信念”起到直接和间接影响作用，但未能直接影响教师关于“学生问题提出数学学习的信念”[40]．

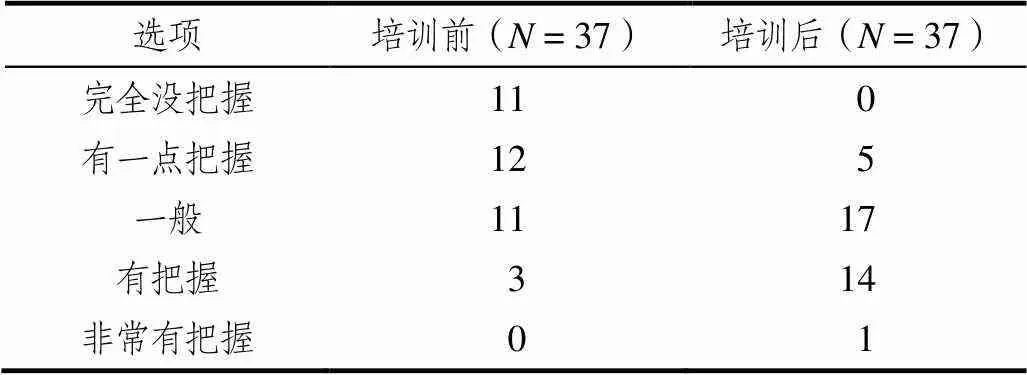
表3 将问题提出整合到教学中的把握程度

注：对于卡方检验，由于有某个数据为0，将“完全没把握”和“有一点把握”结合起来；类似的，将“有把握”和“非常有把握”结合起来．

4.2.3 教师课堂教学的转变

工作坊开始之前，学员提交的教学设计并没有问题提出的元素，说明他们先前并未利用问题提出教授该内容的经验，甚至没有问题提出教学的经验．经过第一期工作坊，学员开始不同程度地将问题提出渗透到教学设计的不同环节[39]．第二期工作坊结束后的调查结果显示，两期都参加的31名学员中，仅有6%的教师还未将问题提出运用于数学课堂教学．在第三期工作坊结束后对已经参加3期的学员展开调查，所有学员表示都已经在运用问题提出进行数学课堂教学，其中还有教师将之用到了课后作业中，从中不仅发现了孩子们很奇特很有趣的想法，同时也发现孩子们对生活中的数学关注紧密，学生也表示非常喜欢这样的作业．第四期工作坊教师的课堂实录充分说明，经由3期问题提出工作坊的学习，教师已经在实际课堂中运用问题提出开展数学教学．

5 不足与展望

这项研究是一项大型项目的前期研究，基于“问题提出”的主题式教师专业发展的探索实践尚处于起步阶段．经过4期小学数学问题提出教学工作坊的实践，尽管对参加问题提出教学工作坊教师的调查结果表明教师的问题提出知识、信念及教学行为都有所改进，但其改进效果并不如预期，仍然面临诸多挑战．工作坊秉持自愿参加的原则招募学员，虽然最大限度地激发了学员的自主性与积极性，但同时由于缺乏约束力造成了部分学员的流失，如何加强顶层设计以及培训管理以保证培训学员的稳固性成为未来工作坊需要解决的首要问题．此外，研究未能追踪学员返岗后的问题提出课堂教学实际，工作坊在给学员带来课堂教学改变的同时是否真正引起学生问题提出能力及其它方面的变化依然未知，这也是该项目下一阶段的研究方向，将继续追踪学员的教学实际及其对学生产生的影响．

基于“问题提出”的主题式教师专业发展为其它学科“问题提出”教师培训项目的开展并助推问题提出落地提供了有益启示．需要强调的是，从实践中总结出来的既定模式虽然可以指导广大研究者，但研讨问题、解决问题要从实际出发，根据实际灵活地、创造性地运用这些原则、模式，要淡化形式，注重实质[41]．

[1] EINSTEIN A, INFELD L. The evolution of physics [M]. New York, NY: Simon and Schuster, 1938: 95–96.

[2] ROSENSHINE B, MEISTER C, CHAPMAN S. Teaching students to generate questions: A review of the intervention studies [J]. Review of Educational Research, 1996, 66 (2): 181–221.

[3] CAI J, HWANG S, JIANG C, et al. Problem posing research in mathematics: Some answered and unanswered questions [M] // SINGER F M, ELLERTON N, CAI J. Mathematical problem posing: From research to effective practice. New York, NY: Springer, 2015: 3–34.

[4] 张玲，宋乃庆，蔡金法．问题提出：基本蕴涵与教育价值[J]．中国电化教育，2019（12）：31–39．

[5] NCTM. Curriculum and evaluation standards for school mathematics [M]. Reston, VA: NCTM, 1989: 22–28.

[6] NCTM. Professional standards for teaching mathematics [M]. Reston, VA: NCTM, 1991: 90–100.

[7] NCTM. Principles and standards for school mathematics [M]. Reston, VA: NCTM, 2000: 20–30.

[8] 日本文部科学省．中学校学習指導要領解説数学編[EB/OL]．（2008–10–10）[2019–10–17]．http://homepage.kokush ikan.ac.jp/rio/user/kks_rio/COS/h20mid1.pdf．

[9] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：8．

[10] CAI J, JIANG C. An analysis of problem-posing tasks in Chinese and US elementary mathematics textbooks [J]. International Journal of Science and Mathematics Education, 2017, 15 (8): 1 521–1 540.

[11] 许天来，蔡金法．美国数学课程中的“问题提出”——期望与挑战[J]．数学教育学报，2019，28（2）：18–23．

[12] 李欣莲，宋乃庆，陈婷，等．小学数学教师“问题提出”表现研究[J]．数学教育学报，2019，28（2）：1–6．

[13] 王定华．新时代我国中小学教师国培的进展与方略[J]．全球教育展望，2020，49（1）：54–61．

[14] 林媛媛，张克明．贫困地区幼儿教师培训状况与发展建议[J]．学前教育研究，2012（1）：28–32，38．

[15]  CAI J, HWAN S. Learning to teach through mathematical problem posing: Theoretical considerations, methodology, and directions for future research [J]. International Journal of Educational Research, 2019（1）：1．

[16] 蔡金法，姚一玲．数学“问题提出”教学的理论基础和实践研究[J]．数学教育学报，2019，28（4）：42–47．

[17] 吴卫东，徐颂列．主题·反思·参与——教师培训模式的实践研究[J]．教育发展研究，2006（3）：58–61．

[18] 吴伦敦，葛吉雪．中小学教师主题式培训模式：内涵与结构[J]．教师教育论坛，2016，29（1）：85–89．

[19] 唐良平，宋素珍．聚焦主题的“四构三研”课例研修的实践研究——以Y区思想品德课教师活动设计价值与策略主题式研修为例[J]．中小学教师培训，2017（3）：20–24．

[20]  GUSKEY T. Analyzing lists of the characteristics of effective professional development to promote visionary leadership [J]. NASSP Bulletin, 2003, 87 (637): 4–17.

[21]  CAI J. Longitudinally investigating the effect of teacher professional development on instructional practice and student learning: A focus on mathematical problem posing [Z]. Newark, DE: The University of Delaware Unpublished Manuscript, 2017.

[22]  YOON K, DUNCAN T, LEE S, et al. Reviewing the evidence on how teacher professional development affects student achievement (Issues and answers report REL 2007–No. 033) [R]. Washington, D.C.: U.S. Department of Education, Institute of Education Sciences, National Center for Education Evaluation and Regional Assistance, Regional Educational Laboratory Southwest. Retrieved from http://ies.ed.gov/ncee/edlabs., 2007.

[23]  DESIMONE L, PORTER A, GARET M, et al. Effects of professional development on teachers’ instruction: Results from a three-year longitudinal study [J]. Educational Evaluation and Policy Analysis, 2002, 24 (2): 81–112.

[24]  CORCORAN T. Transforming professional development for teachers: A guide for state policymakers [M]. Washington, DC: National Governors’ Association, 1995: 70.

[25]  CARPENTER T, FENNEMA E, PETERSON P, et al. Using knowledge of children’s mathematics thinking in classroom teaching: An experimental study [J]. American Educational Research Journal, 1989 (26): 499–531.

[26]  VESCIO V, ROSS D, ADAMS A. A review of research on the impact of professional learning communities on teaching practice and student learning [J]. Teacher and Teaching Evaluation: An International Journal of Research and Studies, 2008, 24 (1): 80–91.

[27] 钟启泉．教师研修的挑战[N]．光明日报，2013–05–22（16）．

[28]  DARLING-HAMMOND L, WEI R, ANDREE A, et al. Professional learning in the learning profession: A status report on teacher development in the united states and abroad [R]. Dallas, TX: National Staff Development Council, 2009.

[29]  GARET M, PORTER A, DESIMONE L, et al. What makes professional development effective? Results from a national sample of teachers [J]. American Educational Research Journal, 2001, 38 (4): 915–945.

[30]  BRYK A, CAMBURN E, LOUIS K. Professional community in Chicago elementary schools: Facilitating factors and organizational consequences [J]. Education Administration Quarterly, 1999 (35): 751–781.

[31] 崔允漷，王中男．学习如何发生：情境学习理论的诠释[J]．教育科学研究，2012（7）：28–32．

[32]  BORK H. Professional development and teacher learning: Mapping the terrain [J]. Educational Researcher, 2004, 33 (8): 3–15.

[33]  LIVIONGSTON K. The complexity of learning and teaching: Challenges for teacher education [J]. European Journal of Teacher Education, 2017, 40 (2): 141–143.

[34]  BRKY A, GOMEZL M, GRUNOW A, et al. Learning to improve: How America’s schools can get better at getting better [M]. Cambridge, MA: Harvard Education Press, 2015: 30–68.

[35]  CAI J, MORRIS A, HOHENSEE C, et al. Using data to understand and improve students’ learning: Empowering teachers and researchers through building and using a knowledge base [J]. Journal for Research in Mathematics Education, 2018, 49 (4): 362–372.

[36] 钟启泉．教师研修：新格局与新挑战[J]．教育发展研究，2013，33（12）：20–25．

[37]  PUTNAM R, BORKO H. What do new views of knowledge and thinking have to say about research on teacher learning [J]. Educational Researcher, 2000, 29 (1): 4–15.

[38] 张姝，邓淑予．论教师培训评估体系的网络结构与运行策略[J]．四川师范大学学报（社会科学版），2020，47（3）：103–109．

[39]  CAI J, CHEN T, LI X, et al. Exploring the impact of a problem-posing workshop on elementary school mathematics teachers’ problem posing and lesson design [J]. International Journal of Educational Research, 2019 (2): 4.

[40] 周菀婷．主题式工作坊对数学教师“问题提出”教学信念的影响研究[D]．重庆：西南大学，2020：61–62．

[41] 宋乃庆，陈重穆．再谈“淡化形式，注重实质”[J]．数学教育学报，1996，5（2）：15–18．

The Development and Conceptualization of Theme-Based Teacher Professional Learning to Teach Through Problem Posing in Elementary Mathematics

SONG Nai-qing1, ZHANG Sha-sha1, CHEN Ting2, LI Zhong-ru3, CAI Jin-fa4, 1

(1. School of Mathematics and Statistics, Southwest University, Chongqing 400715, China;2. Faculty of Education, Southwest University, Chongqing 400715, China;3. Faculty of Teacher Education, Southwest University, Chongqing 400715, China;4. Department of Mathematics, University of Delaware, Newark DE 19716, USA)

With the increased emphasis on mathematical problem posing in school mathematics, there is a critical need for teachers to learn to teach through problem posing. In this paper, we discuss the development and conceptualization of Theme-Based Teacher Professional Learning to Teach Through Problem Posing. Theme-Based Teacher Professional Learning has two meanings: The first is teaching through problem posing, and the second is the focus on content in the teacher professional learning. Based on a series of teacher professional development workshops, this paper discusses the initial attempt to implement Theme-Based Teacher Professional Learning to Teach Through Problem Posing for elementary mathematics teachers and then presents the initial findings about teachers’ perceived effects of the series of workshops on their understanding of problem posing and teaching through problem posing.

problem posing; theme-based teacher professional learning; elementary mathematics; teacher professional development

G622.0

A

1004–9894（2021）01–0012–07

宋乃庆，张莎莎，陈婷，等．基于“问题提出”的小学数学教师主题式专业发展：理论建构与实践探索[J]．数学教育学报，2021，30（1）：12-18．

2021–01–02

国家社科基金后期资助项目——中小学问题提出的理论与实践探索（20FJKB006）；教育部教师工作司新时代中小学教师培训标准研究（40301818）；西南大学引进人才（教育部“长江学者”讲座教授）计划项目（SWU118118）；中国乡村教师支持计划（2015—2020）落实情况调研评估（2019-06-002-BZPK01）；小学数学教师“问题提出”教学能力测评模型构建研究（2021-06-020-BZPK01）；西南大学基本科研业务费专项资金项目——西藏初中生数学学业质量监测研究（SWU1709664）；北京师范大学中国基础教育质量监测协同创新中心自主课题资助

宋乃庆（1948—），男，浙江杭州人，教授，博士生导师，主要从事数学教育、教育统计、基础教育研究．蔡金法为本文通讯作者．

[责任编校：周学智、陈汉君]