浅谈液桥在土颗粒间的作用规律

孙广利 尹思元

吉林建筑大学（130118）

1 研究背景

土材料作为一种典型的颗粒材料广泛地存在于自然界之中，它是由具有不同粒径尺寸的土颗粒组成，而在一般情况下，土颗粒被多种颗粒间作用力所胶结，从而形成具有不同形状、不同性质的土颗粒凝聚物。 对于黏性土而言，其抵抗剪切破坏的能力大部分取决于水分子与土颗粒间的相互作用。大量的水分子吸附在土颗粒上使其成为湿颗粒，当湿颗粒相互积聚时，其间就会产生名为“液桥”的毛细作用力。如今学者们已经开始对液桥展开一系列的研究，并且根据液桥的作用机理对土的力学性质进行推断。

2 研究现状

湿颗粒通过液桥相互连接，非饱和土作为一种典型的湿颗粒材料， 液桥对其性质有着巨大的影响。 国内外诸多学者对湿颗粒开展了大量的研究，Mitarai N、孙其成等人[1-2]认为，范德华力、静电力、双电层作用力、离子水化作用力、胶结作用力等分子尺度的作用力和颗粒间液桥产生的毛细作用力都可作为湿颗粒间的相互作用力；张昭等人[3]认为，为了更方便、更准确地计算液桥作用力，可将土颗粒简化为直径不同的球状颗粒；Lechman 等[4]对颗粒间液桥的体积和毛细力进行了理论研究；栾茂田等[5-6]基于颗粒间液桥的受力分析推导出了持水曲线的理论模型，并研究了张力、吸力和基质吸力与固-液接触角的关系；贺炜等[7]研究了固-液接触角与持水曲线的关系。

目前，学者们对液桥模型的研究已经从等径颗粒过渡到不等径颗粒。土是各种不同大小颗粒的混合物，所以依据各种数学模型和理论，以不等径颗粒作为研究对象更具准确性和代表性。

2.1 液桥计算方法

将Pietsch[8]用颗粒间距2 s 来描述等径粗糙颗粒表面粗糙度的方法推广到不等径粗糙颗粒， 在忽略重力和浮力影响的前提下， 提出一种表征不等径湿颗粒与液桥相互作用的理论模型。 液桥的表面形状在该模型中假定为圆环， 液桥的体积以及基质吸力和颗粒的半径比、固-液接触角和表面粗糙度对毛细作用力的影响规律为研究主体。

图1 一对相互接触的不等径粗糙颗粒间形成的液桥

图2 一对不等径球体颗粒间液桥的几何形状及受力状态

湿颗粒表面的粗糙度， 可以用颗粒间距2 s 来描述。 所以假设有一对直径不相等且表面光滑的球体颗粒（半径分别为R 和nR，n 为颗粒半径比），两颗粒间的液桥如图2 所示。 点O1和O2分别为颗粒1 和颗粒2 的球心；圆弧状气-液交界面的中心在点O3处； 两颗粒与固-液交界面的接触位置分别为点P1和P2；射线O1P1和O2P2交于点U，且两条射线与坐标轴O1O2的交点为点A1和点A2；垂线O3B分别与圆弧P1P3P2和坐标轴O1O2交于点P3和点B，两颗粒内x 轴和y 轴的原点为点B。 对于形成稳定液桥的充填角，会受到其他参数的制约，就此模型而言，当颗粒半径比为n、颗粒1 和颗粒2 的固-液接触角为θ1和θ2时，满足条件的充填角仅有一组，为β1和β2。 与等径颗粒相比，不等径颗粒间的液桥关于坐标轴O1O2对称，较为复杂。

由图2 中三角形O1UO2的几何关系可得到β1和β2之间的关系式:

式中:S=s/Rm为无量纲颗粒半间距（Rm=(R+nR)/2 是这对不等径颗粒的颗粒平均半径）。 假设气-液交界面的形状近似为圆环，则两个给定控制半径的圆弧可以较为精确地描述液桥的形状。 我们可以用如下的无量纲表达式表达两个不同材料的不等径球体颗粒间的液桥:

图2 中两个接触点间的凹液面P1P3P2绕x 轴旋转的体积与圆弧P1T1和P2T2绕x 轴旋转所形成的两个球冠的体积之差即为不等径球状颗粒间液桥的体积。 液桥表面的无量纲旋转体体积Vmp为:

式中，Yxi为αi的函数，表达式为:

颗粒被液桥浸润的两个球冠的总无量纲体积Vss为:

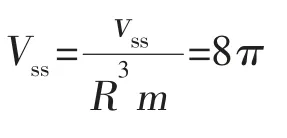
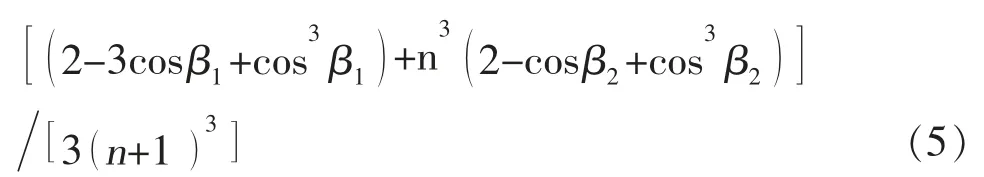
综上所述，液桥的无量纲总体积Vl为:

2.2 液桥从形成至断裂的毛细规律

根据张昭等人的研究[9]，无量纲液桥毛细力f关于无量纲液桥体积vLB和固-液接触角θ的表达式为:

可绘制当f=0 时固-液接触角θ与vLB之间的关系曲线，如图3 所示，将液桥划分为形成区和断裂区。vLB和θ决定颗粒间的毛细力作为引力或者斥力出现。

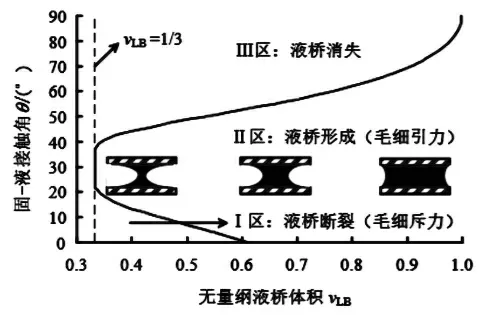
图3 采用式（7）且令 f=0 时绘制的 θ 与vLB 关系曲线及其对液桥毛细力划分的3 个区域

2.2.1 I 区: 液桥断裂区（毛细斥力）（1/3＜vLB≤0.61，0°≤θ＜22.4°）

在此区域内，液桥毛细的作用力小于零，为负值，即f<0（毛细斥力）。由于颗粒间的毛细联结作用会受液桥稳定性降低的影响而减弱，使其间的持水量减少，所以液桥断裂的毛细力（基质吸力产生）与促进液桥形成的毛细力（表面张力产生）之间的排斥作用会使黏土颗粒间液桥的稳定性被削弱， 直至断裂。

2.2.2 II 区:液桥形成区（毛细引力）（vLB=1/3，22.4°≤θ＜37.6°）

此区域内，液桥毛细作用力大于零，为正值，即f>0（毛细引力）。 与I 区情况相反，由于颗粒间毛细胶结作用受液桥形成的影响， 并导致持水量增多，所以液桥断裂的毛细力（基质吸力产生）与促进液桥形成的毛细力（表面张力产生）之间的吸引作用会使液桥在黏土颗粒间产生。 毛细引力值越大，液桥稳定性越好，颗粒间的毛细胶结作用越强。

2.2.3 III 区:液桥消失区（1/3＜vLB≤1.0，37.6°＜θ≤90°）

此区域内，水以薄膜形态附着于黏土颗粒表面（黏土的持水特性进入吸附阶段），不再以液桥的形式存在于颗粒间。

2.3 液桥对土颗粒力学性质的影响

Bishop 所给的非饱和土有效应力的定义为:

式中，σ' 为有效应力，σ为总应力，χ为水压力作用的面积分数。

苗天德[10]慕青松[11]等人在该式的基础上添加了水膜张力λ的作用影响，将该式重新修改为:

式中，s=χ(ua-uw)+λ为总吸力。

假设土颗粒相互接触形成一个表面粗糙的接触界面， 在该界面上有数量为n 个的颗粒间液桥，用Fi（i=1，2，…，n）代表液桥的毛细作用力，用θi（i=1，2，…，n）代表液桥轴线与统计平均平面A 的法线之间的夹角，则由多个液桥毛细作用力形成的总吸力表达式为:

土的抗剪强度的摩尔-库伦准则为:

式中，φ' 为有效摩擦角，c' 为其他作用 （色散力、电磁力、盐分胶结力等）引起的粒间粘聚力。

根据慕青松等人的研究[12]，土的抗剪强度随基质吸力的增大而增大， 但增大的趋势逐渐趋于平缓，呈非线性渐减增长趋势。 假设有这么一种模型土， 由粒径为D1、D2的两种球形颗粒均匀混合组成。

模型土总质量为:

式中，m1和m2分别为两种球形颗粒的质量，a1和a2分别为两种球形颗粒的质量分数。

两种颗粒的个数分别为:

定义两种颗粒的总表面积分别为:

假设在同一基质吸力ua-uw下，对该模型土，在截面A上D1与D1接触点、D2与D2接触点以及D1与D2接触点所形成的液桥个数分别为N11、N22与N12，假设液桥轴线在各方向上均匀分布，则总吸力表达式可改为:

接触点上的吸力表达式为:

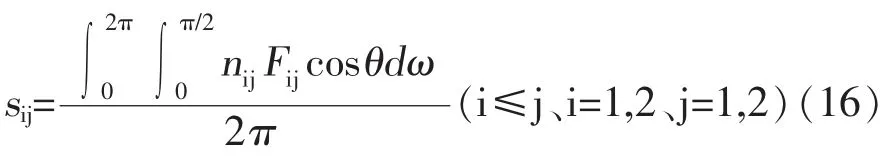
用上述公式根据颗分曲线选取两种不同粒径的颗粒， 假设两种颗粒在土样中占据不同的百分比，依次计算基质吸力，并绘制基质吸力与粘聚力的关系曲线。 结果表明上述公式的计算结果符合粘聚力随基质吸力的增大而增大的特点，并且增长趋势逐渐减缓。

3 展望

综合各学者的研究结果，可以将液桥毛细力作为评判黏性土力学性质强弱的依据之一，其可以从细观上更好地描述土颗粒之间的作用力，从而反映出非饱和土在水的作用下的毛细作用力。 并且根据液桥的作用机理对土的力学性质进行推断。