基于ConvLSTM的气象雷达回波外推

李英睿，李 琼，魏加华，3*，乔 禛，申惟文

(1.青海大学土木工程学院，青海 西宁 810016；2.省部共建三江源生态与高原农牧业国家重点实验室，青海大学，青海 西宁 810016；3.清华大学水沙科学与水利水电工程国家重点实验室，北京 100084)

雷达回波外推是临近降水预报的主要手段，原理是利用雷达探测到的回波数据，确定回波的强度分布及回波体的移动速度和方向，通过对回波体进行线性或非线性的外推，预报一定时间段后的雷达回波状态。传统的雷达回波外推中交叉相关法[1-2]对数据利用率低，对于速度梯度大、演变快的回波，反演误差大，难以推演实际天气状况。质心跟踪法[3-4]在稳定性降水预报中可以取得较好效果[5]，但在局部地区对流天气中，回波发展演变较快，无法满足守恒条件，预报效果会随时间的变化快速下降[6-7]。光流法[8]是从连续的图像序列中计算光流场[9]，利用图像序列中像素在时间域上的变化及相邻帧之间的相关性，建立上一帧跟当前帧之间存在的对应关系，再计算出相邻帧之间物体的运动信息。为提高预测效果，基于神经网络方法进行临近预报是目前研究的热点[10]。Ayzel等[11]提出各层卷积核数量不同的6层全卷积Dozhdya.Net模型，采用零填充保持空间分辨率，与光流法相比在预报上具有更高的精度。陈家慧等[12]将BP神经网络模型应用于混合型降水回波的外推，从历史回波数据中学习得到回波运动的特征。施恩等[13]提出基于输入的动态卷积神经网络模型(DCNN-1)，与传统回波外推方法相比，该方法有更高的预测精度且能有效延长外推时效。Shi等[14]提出基于LSTM的ConvLSTM(Convolutional Long Short-Term Memory，ConvLSTM)神经网络结构，预测精度高于光流法。相比于传统方法[1-4]，使用神经网络进行回波预测，具有数据利用效率高、预报精度准确、优化潜力大等优势。

本文利用2019—2020年雷达体扫数据，通过数据预处理，建立样本库。利用ConvLSTM回波外推模型，实现基于雷达回波数据的预测，并与光流法对比，评价回波在不同时间上的预测精度，分析误差随外推时间及海拔高度的变化趋势，探讨深度学习模型在雷达回波预报上的适用性。

1 实验数据

雷达位于青海大学校内(101.74°E，36.72°N)，海拔2 301 m。雷达有效探测半径50 km，24 h以VOL方式运行，5 min内可完成从0.5°～19.4°的14个仰角360°扫描。雷达采用抬升仰角和波束扫描的观测方式，回波由波束抬升和距离变化发生衰减。将三维极坐标系的数据转至笛卡尔坐标系，并进行波束遮挡以及杂波抑制等预处理工作，以提高雷达数据的利用率，最大可能地保留雷达原始数据的结构特征。

1.1坐标转换假设目标在雷达站A的极坐标系中坐标为(ρ，α，β)，其中ρ为斜距，α为方位角，θ为仰角。目标在雷达站A直角坐标系中的坐标为(x，y，z)，则变换公式：

(1)

由式(1)投影后得到雷达的三维空间格点数据[15]。经过坐标转换后的雷达网格数据分布散乱，为便于后续计算，采用最邻近插值算法生成标准的网格数据，水平和垂直方向网格大小均为500 m×500 m。

1.2波束遮挡雷达波束在传播过程中遇到障碍物(如高山、建筑物等)或地物干扰，导致雷达发射的电磁波束受到局部或全部遮挡。波束被遮挡会导致观测信号失真，探测数据质量受到影响。图1a为雷达半径50 km的扫描范围中的DEM数据，低仰角时波束会被附近山体遮挡，同时地物杂波对雷达回波产生较大干扰。为减少波束遮挡影响，实测时调整雷达俯仰缩减探测范围，以提高数据质量，并以 20 km范围内的高仰角扫描数据(图1b)为研究对象。此外，雷达回波预报时效以1 h内最为理想，且回波与700 hPa的气流有强相关性[16]。经过综合分析，选取海拔高3 000 m高度以上的数据进行雷达回波外推。

图1 雷达扫描区域及不同海拔波束遮挡情况Fig.1 Radar scanning area and beam occlusion at different altitudes

1.3地物杂波抑制地物杂波是雷达观测中由地表物体(如植被、岩石、山体等)引发的异常噪声信号，是复杂地形条件下经常常遇到的雷达观测误差。固定地物杂波引起的噪声会长期存在，对降雨的估计带来一定误差。地物杂波通常发生在距离雷达较近的区域内,且固定地物引起的杂波信号具有径向速度接近为零等特征[17]。经过综合分析，在以雷达为中心的20 km的扫描范围内，将径向速度等于零的值标记为杂波干扰值，反射率因子的值视为无效值。图2为2020年5月9日的晴空雷达回波数据，通常晴天雷达扫描过程中不会出现回波，故将晴空回波认为是杂波干扰，图2a和2b分别为杂波去除前和除去后的对比图。

图2 2020年5月9日晴空雷达回波去除杂波前后对比Fig.2 Comparison of radar echo of clear sky before and after removing the clutter on May 9，2020

2 实验方法

图3 ConvLSTM结构示意图Fig.3 Schematic diagram of ConvLSTM structure

2.1ConvLSTM长短期记忆网络(Long Short-Term Memory，LSTM)是一种常用来处理序列数据的时间循环神经网络(Recurrent Neural Network，RNN)。本文选用Shi等[14]提出的ConvLSTM网络结构,与用于一维时间序列数据的LSTM模型结构不同，该模型将卷积与LSTM相结合，将信息传递时的全连接计算改为卷积计算，使其在时间和空间维度上均具有捕捉特征的能力。图3为ConvLSTM的结构，采用与LSTM相似的门控单元控制当前输入特征是否传递下去。ConvLSTM的3个门结构分别为遗忘门(ft)、输入门(it)和输出门(Ot)，Ct是记忆细胞。记忆细胞中不仅保留了当前的输入特征，并通过控制前一时刻的信息是否继续传递，信息传递关系用式(2)表示：

it=σ(Wxi*Xt+Whi*Ht-1+Wci°Ct-1+bi)ft=σ(Wxf*X+Whf*Ht-1+Wcf°Ct-1+bf)Ct=ft°Ct-1+it°tanh(Wxc*Xt+Whc*Ht-1+bc)Ot=σ(Wxo*Xt+Who*Ht-1+Wco°Ct+bo)Ht=Ot°tanh(Ct)

(2)

其中：σ表示sigmoid激活函数，(°)表示矩阵对应元素相乘，*表示卷积操作。本文采用卷积操作对特征进行提取，并通过sigmoid层和点乘运算操作构成的门结构对信息进行选择。信息经过遗忘门sigmoid单元，决定Xt和Ht-1中哪些信息需要丢弃，哪些信息需要继续向后传递；继续传递的信息流入输入门通过sigmoid层决定需要更新的信息，通过tanh层得到新的细胞信息，进行细胞更新；将通过输出门sigmoid层的信息与通过tanh层的记忆细胞中的信息相乘得到模型的最终输出Ht。

2.2光流法光流法将雷达回波映射到0～255的数值区间内，基于光流法的短时回波预测，假设雷达在短时间内的移动趋势不变，计算有位移区域的平均位移矢量，并将空白区域的位移设为平均值，得到各点位移矢量后，将矩阵中各点都按照位移矢量平移，得到新的雷达回波矩阵。因此，要预测 30 min后目标点的像素值，需要迭代重复上述步骤6次，得到的坐标点像素值即为预测目标。

2.3对比方法及指标选取2019年8月—2020年6月中22场降水的雷达回波数据对模型进行训练，6场时间较长的降水过程作为模型的验证，并选取典型降水过程，分析误差在时空上的变化。设计不同模型输入时长，分别采用ConvLSTM与光流法进行不同时间的回波预测，并对外推效果进行对比分析。

由于难以直接量化回波图像预测的准确性，本文采用均方误差MSE评价预测值和实际值的偏差，MSE数值越低，预测效果越好。计算公式见式(3)：

(3)

3 结果与分析

本实验通过改变模型的输入时间(30、60、90、120 min)，采用ConvLSTM和光流法两种方法分别进行2 h(时间间隔30 min)的回波外推；固定ConvLSTM模型的输入时间为30 min时，进行2 h内(每30 min)的回波预测；对选取典型过程回波外推效果和误差进行分析。

3.1回波外推时间过程分析选取2020年6月30日降水中不同时刻的雷达回波数据及评价指标进行对比，雷达回波可以直观地反应预测和实际观测数据的整体变化趋势；评价指标反应整场降雨中误差随时间的变化情况。

模型对输入30、60、90和120 min的雷达回波数据分别进行不同时间的外推。对2020年6月30日降水过程中19∶10、19∶40、20∶10、20∶40和21∶10时的回波进行可视化(图4)。第1行为观测图像，第2行为光流法外推后续第30 min在5个相应时刻的外推回波图像，第3行至第6行分别为对30(ConvLSTM-6)、60(ConvLSTM-12)、90(ConvLSTM-18)及120 min(ConvLSTM-24)的输入时长，进行第30分钟、第60分钟、第90分钟和第120分钟外推在相应5个时刻的回波图像。由图4可知，基于ConvLSTM模型预测结果与实际观测图像相似程度更高；在回波数值较低的区域中，光流法很难准确计算出回波强度较弱区域的矢量场，使得部分结果被低估。但该模型在一定程度上仍存在误差，这是因为雷达回波外推本身有不确定性，虽然ConvLSTM在训练过程中可以捕捉回波在时空上的变化规律，但无法对区域内所有格点做出完全精准的预测，某些位置只能反映出变化趋势。此外，随着外推时间的增加，模型的预测误差逐步累计，从21∶10回波图像中可以直观地看出ConvLSTM-18和ConvLSTM-24对回波预测准确度在不同程度上有所下降，虽然总体趋势与观测图像类似，但仍有不一样的细节特征。

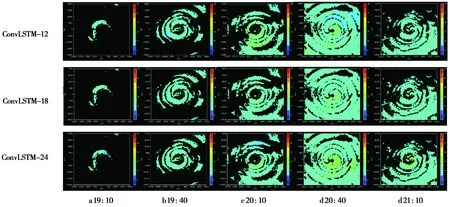
图4 各时刻回波图像对比Fig.4 Comparison of images of echo at different times

选取2020年6月的6场降水过程作为验证集，均方误差随时间的变化如图5a所示。从图中可以看出，随着外推时间的增加，预测误差也增加，ConvLSTM预测结果相对稳定，该模型对特征的学习及预测的误差逐步累积，而光流法的整体预测误差均相对较大。

图5 光流法和ConvLSTM的预测误差对比Fig.5 Comparison of prediction errors between optical flow method and ConvLSTM

综上所述，ConvLSTM预测结果优于光流法，且可以有效延长预测时间。ConvLSTM模型不仅具有传统全连接LSTM网络学习时间特征上的能力，而且还具备捕捉空间特征的能力。光流法在捕捉时间和空间变化特征的能力上稍显不足，原因在于雷达回波数据并非一一对应，存在较强的非线性、时滞性。光流法要求遵循图像灰度不变的假设，雷达回波各时刻都存在升消变化，在不结合云层运动变化的情况下，会出现反射率因子不守恒带来的误差，导致模型难以对测试集进行准确预测。

3.2回波外推空间预测精度分析由于雷达波束抬升，探测高度增大，探测距离和不同海拔回波的预测精度存在差异，本实验选取2020年6月25日的降水过程进行分析回波外推空间预测的精度。ConvLSTM模型与光流法预测结果在不同海拔的误差分布见图6和图7，从左到右、从上到下分别为海拔3 000～5 500 m外推误差空间分布图，层高间隔为500 m。图中ConvLSTM模型在各高度层的误差值均小于光流法，呈现较稳定的预测精度，随着探测高度增加，误差逐渐增大。假定实际值和预测值≤5 dBz时满足精度要求，ConvLSTM模型在1～3层中约有96%的预测误差处于0～5 dBz，4～6层中预测误差处于0～5 dBz的概率下降，第6层中误差≤5 dBz的概率仅有49%。尽管光流法的预测精度较低，68%的格点预测误差在该范围内，但随着高度的增加预测误差仍旧呈现上升趋势。可见，随着探测高度的增加，预报的误差逐步累积。

图6 ConvLSTM模型第30分钟预测在不同海拔高度预测误差累积Fig.6 Cumulation of prediction errors at different altitudes in the 30min prediction of ConvLSTM

图7 光流法第30分钟预测在不同海拔高度预测误差累积Fig.7 Cumulation of prediction errors at different altitudes in the 30min prediction of optical flow method

图8 平均预测误差对比Fig.8 Comparison of average prediction error

两种方法在不同海拔高度中不同预测时长的平均误差如图8所示。海拔3 000～4 000 m高度中的误差均相对较低；海拔3 000 m高度时的预测效果最好，海拔高于4 000 m误差呈现明显的上升趋势。光流法各层的预测误差均值相对较高。在ConvLSTM模型中，利用海拔4 500 m及以上的雷达回波数据，预报准确率下降约为原来的60%左右。从图5b可以看出雷达回波外推在水平方向变化，距离雷达中心越远，误差越大。经过综合分析可知，雷达在本地区海拔4 000 m以下回波预测效果较好；在海拔3 000 m的预测误差最小，表明回波与700 hPa的气流有很强的相关性。

选取2020年6月25日的降水过程分析不同预测时长在水平方向上的误差变化。模型的输入时间恒为30 min，计算海拔3 000 m高度层各时刻第30分钟，第60分钟，第90分钟及第120分钟后的平均预测误差，结果如图9所示。

图9 不同外推时间预测误差变化Fig.9 Variation of prediction error of different extrapolation time

图10 预测误差随时间变化趋势Fig.10 Trend of forecast error over time

图9a～图9d分别为各时刻第30分钟，第60分钟，第90分钟，第120分钟的预测误差累积在海拔3 000 m上的分布情况。从图中可以直观地看出，随着外推时间的增加，误差的累积也在逐渐增大。在图9a～图9d中分别有96.3%、95.5%、95.1%、81.7%的预测误差小于5 dBz，相对误差大于5 dBz的占比也由4%上升至18%左右。图10中，在海拔3 000 m高度层上误差随着外推时间的增加逐步累积，预测误差小于5 dBz的占比整体呈现波动下降趋势，相对误差在数值上逐渐增大。整体来看，对于第30～第90分钟的预测精度误差的整体变化趋势不大，但第60～第90分钟的预测精度比第30分钟略高，在第120分钟时预测的误差值有明显的增加，预测精度较低。

4 讨论与结论

雷达回波外推技术是临近天气预报的主要技术手段，目前深度学习网络在预报领域的应用逐渐增多。本文利用ConvLSTM模型进行雷达回波外推，检验该模型对青海大学X波段天气雷达回波的预测能力。由于降水的形成与发展的过程较为复杂，预报存在较多的不确定因素。从本次实验结果综合来看，该模型对西宁地区的雷达回波数据有着较好的预测精度，在海拔3 000 m高度层的预测精度较高，回波与700 hPa的气流有很强的相关性，该结果与陆汉城等[18]所得结论一致。与传统的光流法的预报结果相比，ConvLSTM模型通过训练能从大量的雷达数据中学习到更多的雷达回波变化时间和空间特征，有效地提高了数据的利用率，对于雷达回波数据有较强的适应性。Shi等[14]通过对比ConvLSTM模型与光流法及其改进方法的预测精度，该模型的精度高于其他对比方法，这与本文研究结果相同。从ConvLSTM模型的外推结果来看，在第1.5小时内的表现较好，误差较低，预报精度满足应用需求，能够在总体上预报降水的变化趋势，这与梁振清等[19]得出ConvLSTM 网络在1h内表现较为良好的结论稍有出入，这可能与西宁地区的降水类型、降水持续时间及云层的影响有关。相比于光流法，ConvLSTM模型能在一定程度学习到特征在空间及时间上的变化趋势，并在一定程度上延长外推时长。ConvLSTM模型对有降水过程的雷达回波预测表现较好，在未来可以针对不同降水强度下雷达回波的变化对模型进行适当的改进，进一步提高模型的准确性与适用性。