引力不变量曲线坐标系及在定位导航上的应用

于锦海，徐 焕，万晓云

1. 中国科学院计算地球动力学重点实验室，北京 100049; 2. 中国科学院大学地球与行星科学学院，北京 100049; 3. 中国地质大学(北京)土地科学与技术学院，北京 100083

地球重力场(或引力场)的研究工作目前已经取得了较大进展。例如：综合利用各类重力观测数据建立了EGM2008模型，重力场的分辨率有了极大的提高。又如：卫星重力技术的应用，特别是GRACE卫星计划的实施，应用时变重力场信息可以解释地球质量的迁移特征[1-2]。此外，重力测量技术也获得了较大的发展，特别是卫星测高技术与重力梯度测量技术的应用[3-6]，为解算重力场提供了丰富的观测数据。所有这些关于重力场方面的进展，使得进一步地拓展重力场应用成为可能。

重力辅助导航是重力场理论的潜在应用方向之一[7-9]。自20世纪90年代开始，便有国外的学者进行了研究与模拟测试[10-14]，而我国也有学者开展了相应的研究工作[15-16]。若将上述研究工作进一步延伸，能否利用重力理论来实现自主定位与导航(即单纯使用重力测量数据实现目标的定位与导航)。显然，这是一项极有挑战的工作，其中包含了利用重力进行定位与导航的理论问题、重力测量仪器的研制、高精度与高分辨率的重力场模型研发等诸多因素[17]。

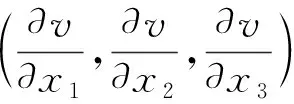
如何建立重力场(引力场)数据与相应空间点位之间的直接关系，以及建立的关系有何应用价值，是能否利用重力数据进行自主定位与导航的基础理论问题。本文的目标从引力场对应的不变量入手，引入一组曲线坐标系，并研究其性质和探讨潜在的应用。因为引入的曲线坐标系是由不变量构成的，因此该坐标系直接描述引力场与空间点位之间直接的关系。

1 引力场的不变量

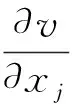
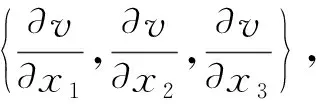
(1)

(2)

经计算，这些不变量可写为[19-20]

(3)

由于引力位v满足Laplace方程，即I1=0，所以从引力梯度数据可构造出函数I2和I3。因为I2和I3是不变量，这意味着I2和I3也仅是点位的函数，与引力梯度分量的方向无关。

至此，就从引力场自身引入了3个仅与点位相关的函数g、I2和I3。由于这3个函数都有各自的物理量纲，所以需进行去量纲化处理。

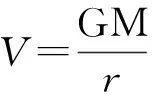
为了确保不变量坐标系(f1,f2,f3)构成了曲线坐标系，需要在理论上证明相应的Jacobi行列式是非零的，即

(4)

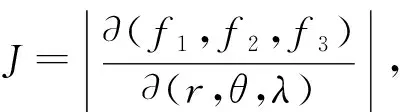
事实上，因为Jacobi行列式J是不恒为零的，所以从三维空间分布看面，J=0仅可能构成空间的曲面，图1的结果表明，该曲面大致是赤道沿径向向外延伸的曲面。

图1 利用EGM2008前180阶次模型计算的Jacobi行列式在地球平均球面上的分布Fig.1 The distribution of Jacobi’s determinant for EGM2008 model with the former 180 degree and order on the average sphere of the earth

2 不变量坐标系与空间点位之间的关系

本节将通过某些实例计算来验证：假若事先给出了不变量坐标系的具体表达式，则利用该表达式就可以进行空间点的定位。正如地图一样，通过对若干参照物的观测可以利用地图作为工具来确定点位的坐标，因此在某种意义上看，不变量坐标系起着地图的作用。

本节将以EGM2008引力场模型的前360阶次作为实际地球引力场，由此便可以得到相应的引力不变量曲线坐标系(f1,f2,f3)。假设在地面上某点P进行引力和引力梯度观测，并进行数据处理后得到了P点在不变量坐标系下的值(F1,F2,F3)，其目标是解算出P点的空间坐标(r,θ,λ)。事实上，从P点的观测值(F1,F2,F3)，可以建立下列方程组

(5)

由于不变量坐标系(f1,f2,f3)是已知的，故通过解算上述方程组便能得到P点对应的球坐标。显然方程组(5)关于待解算的变量(r,θ,λ)是非线性的，因此直接进行求解是难以实现的。理论上讲，对于形式如方程组(5)的非线性方程而言，只要在某点处的Jacobi行列式非零，那么在该点附近是局部可解的，用数学语言描述，就是存在该点的某个邻域，在该邻域内方程组是唯一可解，而且解还具有稳定性[21]。至于求解方法通常是采用Newton迭代法，即线性化迭代解法。

下面就方程组(5)，给出具体的线性化迭代过程如下

(6)

这里j=0,1,2,…，而初始值(r0,θ0,λ0)的选择与待计算的P点要尽可能地接近，其理由就是因为非线性方程组的解仅在局部具有存在性、唯一性、稳定性。在方程组(6)中，待解的量是(rj+1,θj+1,λj+1)，因此方程组(6)关于解算量是线性的，所以方程组(6)称为方程组(5)的线性化迭代形式。由于方程组(6)是线性的，所以其可解性完全取决于在(rj,θj,λj)处的Jocobi行列式J(rj,θj,λj)。如果能通过实际解算验证方程组(6)关于(rj+1,θj+1,λj+1)是唯一可解的，那么便间接地证明了Jocobi行列式是非零的。此外，至于需要进行多少次迭代，这取决于事先给出的误差。事实上，只要迭代前后解的差小于误差要求，便可以停止迭代，从而得到所需的解。

为了验证方程组(5)以及线性化迭代形式(6)的可解性，本文通过3个低、中、高纬度实际点位上的不变量坐标值对其进行了验证，其解算结果汇总见表1—表3。

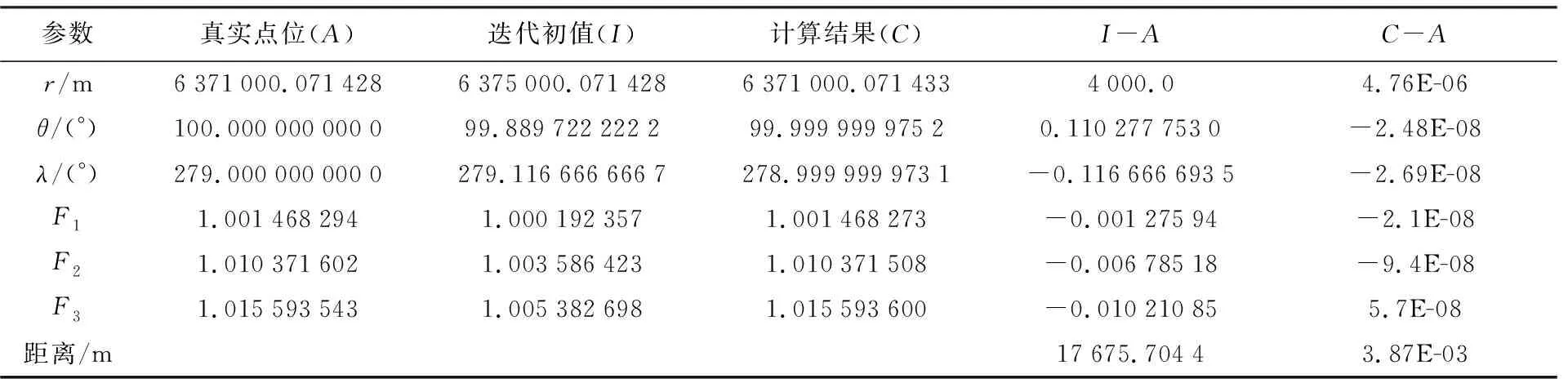
表1 低纬度点验证结果

表2 中纬度点验证结果

表3 高纬度点验证结果

表1—表3中，第1列是点位坐标与实测不变量坐标值的记号，第2列是实际的点位与不变量坐标值，第3列是迭代形式的初始值(r0,θ0,λ0)以及对应的不变量坐标值，第4列是通过迭代解算式(6)后得到结果，第5与第6列则是初始结果和最终计算结果分别与实际值的差，而最下面的行(距离)则是误差。表1表明，对于低纬度点，迭代初始值的点位距实际解算点位17.676 km，通过迭代计算后得到的最终点位坐标与实际点位的差仅有3.87 mm。表2表明，对于中纬度点，迭代初始值的点位距实际解算点位32.634 km，通过迭代计算后得到的最终点位坐标与实际点位的差仅有1.34 mm。表3表明，对于高纬度点，迭代初始值的点位距实际解算点位42.519 km，通过迭代计算后得到的最终点位坐标与实际点位的差仅有7.69 mm。为了清晰地反映迭代求解过程，本文将表1—表3中的计算迭代过程与次数汇制成图2。从图2能清晰可见关于低、中、高纬度点位的迭代解算过程，此外迭代次数分别是4、3、9次。

图2 迭代求解过程Fig.2 Graphical processes of iteration

通过上述关于低、中、高纬度点的验证，可得到如下结论，若事先能给出不变量坐标系，那么通过重力与重力梯度观测是可以反解出空间点的位置坐标的，这为单纯利用重力数据进行自主定位导航提供了新的途径。

需要说明的是：①若出现Jacobi行列式为零的情况，那么本文给出的方法将无法反演出点位坐标，如图1所示，在赤道附近有可能会出现这样的情况；②诸如引力(重力)和梯度测量是可以连续实施的，因此在求解线性化方程组(6)时其初始值通常应该取为上一个点位的坐标，这样就能保证初始值与定位点的距离差距不大。

3 结论与潜在的应用

本文利用地球引力场(或重力场)的性质，描述了相应的引力不变量曲线坐标系。利用该坐标系，可以进行空间点位的反演计算。事实上，不变量坐标系在定位时就像地图一样，是需要事先确定的。不同的是，地图是纸质或数字形式表现出来的，而不变量坐标系是以函数形式表现出来的。若要将本文论述不变量曲线坐标系用于实际定位与导航应用，大致需要进行下列几项工作：①通过各种引力(重力)测量方法来获取相关数据，对其进行处理后给出不变量坐标系的表达形式；②在进行实际定位或导航时，需要进行实时的引力与引力梯度测量，即需要精度满足要求的加速度计和梯度测量仪器；③采用理论上可行的算法，利用事先建立的不变量坐标系与实时测量值来反演点位的坐标。本文工作主要是论证上述方法在理论上的可行性，并针对第3部分内容进行分析与讨论。

如何事先给出引力(重力)不变量曲线坐标系，这取决于地球引力场(重力场)模型的建立。如果建立了精度足够高的引力场(重力场)模型，则利用该模型自然就可以生成不变量坐标系。目前EGM2008重力场模型已经达到了2160阶次，分辨率可达8 km左右，而国内和国际上即将推出更高阶次的重力场模型，这对于建立高精度的全球不变量曲线坐标系无疑有着直接的作用。对于局部问题(例如南海区域)可以通过在该区域进行高分辨率的重力测量，结合卫星海洋测高数据解算出区域重力场模型，例如，可采用球冠谐级数模型或移去恢复法建立局部模型[22-26]，由此便可得到局部区域相应的不变量坐标系。总之，要实现事先能给出不变量曲线坐标系，需要进行大量的实际测量、数据处理等系列工作，正如要绘制出精确的地图一样，需要事先完成系列工程性的工作。显然，这不是本文能够解决的问题。

为何引入引力梯度不变量作为曲线坐标系，而不是采用梯度的分量。这是因为梯度分量不仅与点位有关，而且依赖于方向，这会导致更多参数的引入。单纯从数学角度讲，若使用梯度分量，则对应数组已不再是曲线坐标系的概念了。从实际应用看，更多参数的引入会增加理论与计算的复杂性，甚至会导致欠定问题，即给出的条件数少于待解未知数的个数。

在引力不变量曲线坐标系中，引力(重力)是可以直接测量的，而引力(重力)梯度不变量I2和I3则是梯度分量的组合。事实上，文献[20]曾证明：计算I2和I3仅需梯度的3个对角分量vrr、vθθ和vλλ即可，理由是这3个对角分量是梯度分量的主项，其余分量的计算可利用重力场模型迭代计算来解决。对于该3个对角分量，由于径向r与引力(重力)的反方向相差不大，所以可以利用垂线方向作为标定轴向，其余两个轴向只要与标定轴垂直即可。总之，在计算不变量I2和I3时，梯度的3个对角分量是必不可少的。概括来说，若在某点给出了引力以及3个梯度对角分量(共4个观测量)，则可以算出该点处的不变量坐标值，从而解出该点的空间坐标位置。如果不采用不变量坐标系，需要解算的量是坐标位置(3个分量)和梯度姿态(3个欧拉角)共6个未知数，因此将导致欠定问题，即4个观测量，6个未知数。

至于第2项主要工作，即加速度计与梯度测量仪器的研制与应用，显然是能否将本文提出的方法予以实施的关键。对于引力(重力)测量，微伽级精度的加速度计已经用于实际测量，因此引力测量的条件是具备的。关于引力(重力)梯度测量，目前得到应用的最好成果当属GOCE卫星上搭载的梯度测量仪[27]，其精度能达到几个mE(10-12s-2)量级[3]。此外，美国Maryland大学[28]在实验室里研制出了精度达到0.14 mE的重力梯度仪，而我国也有研究机构正致力于重力梯度仪的研制。期待不久的将来，能生产出可用于实际测量的重力梯度仪。

本文的目的是阐述单纯利用引力场(或重力场)理论进行自主定位与导航的可行性。尽管学术界已经提出过重力辅助匹配导航的思路，但是以曲线坐标系的形式进行引力场(重力场)独立定位导航的思路尚属首次提出，这对于拓展重力场的应用无疑是有益的。