顾及噪声密度函数差异的自适应回归算法及其在人工标靶提取中的应用

贾象阳，黄先锋，牛文渊，张 帆，高云龙，杨 冲

武汉大学测绘遥感信息工程国家重点实验室，湖北 武汉 430079

在测量工程中，回归算法经常被用于解决含有噪声的数据模型参数估计问题，其中，经典的RANSAC算法[1]凭借其实现简单和稳健等优势在图像匹配[2-3]、点云定向[4-6]、三维模型修复[7]和机器人定位抓取[8]等领域有着广泛应用。

根据经典RANSAC算法的假设-验证策略，所有RANSAC改进算法针对3个方面进行优化，包括：①优化假设模型[9-11]，②改进验证策略[12]，③降低时间成本[13]。LO-RANSAC[9]、OR-RANSAC[14]和U-RANSAC[15]算法通过改进采样的方式优化初始假设模型，提高模型参数估计精度的同时，也降低了时间成本。与之类似的算法还有NAPSAC[11]、PROSAC[10]、GOODSAC[16]及SCRAMSAC[17]等，他们都在内群点比噪声点更加紧凑的前提下对模型参数进行估计。在文献[12]基于内群点服从无偏高斯分布以及噪声服从均匀分布的假设提出MLESAC算法之后，MAPSAC[18]、RMLESAC[19]、AMLESAC[20]、u-MLESAC[21]和SASAC[22]等算法对内群点比率(γ)和方差(σ2)的精度和稳健性进行了优化，试验效果显著。基于文献[12]的假设，文献[23]提出一种基于NFA(number of false alarms)的对抗策略，保证了内群点比例自适应的同时，对采样策略和模型评定准则也进行了改进,但是，仍然需要人工给定阈值(如：NFA阈值)。另外，有些学者对传统RANSAC算法进行优化，不考虑数据分布情况，比如：文献[24]通过穷举一定范围内的误差容忍阈值，并采用固定迭代次数的方式估计模型参数方差，最小方差对应的误差容忍阈值与模型参数作为最优估计。

但是，现有的RANSAC改进算法在寻求最优回归模型时都需要人工给定先验信息，这对于算法精度、效率、稳健性及普适性都会造成不同程度的影响。基于此，本文提出了一种参数自适应的RANSAC算法，不需要给定任何先验信息，在保证不降低迭代有效性的情况下，模型回归精度要优于现有算法，并分别通过仿真模拟和真实场景进行了对比试验分析。

1 算法原理

基于文献[11]的假设：相较于噪声，内群点在空间中分布更加紧凑(相比于噪声，①内群点平均密度或数量通常更大；②内群点分布与给定模型更加吻合)。本文提出一种空间密度函数，用于描述点云空间分布与密度之间的关系，并自适应地估计模型参数,技术路线见图1。

注: 灰色矩形框表示本文的改进和优化之处，整体为原始RANSAC的流程。

(1) 遍历原始数据集，统计并计算每个点的邻域半径(详见1.1节解释)以及搜索半径，选取落在搜索半径内的点个数作为采样权重。

(2) 改变传统RANSAC算法仅依赖内群点数量判断模型好坏的方式，根据内群点的空间密度信息表征，联合误差与内群点分布判断模型的好坏。

(3) 利用空间密度函数计算其终止条件，其算法见算法1。

算法1 基于空间密度函数的自适应RANSAC算法

变量：模型:M,最优模型:best_M,内群点:inliers,最优内群点:best_inliers;最优误差容忍阈值:best_α;本次误差容忍阈值:α;上一次误差容忍阈值:α′;散乱点云:spc;容忍失败率:ε;迭代次数:t;本次空间密度:ρ;上一次空间密度:ρ′;点到当前M的符号距离:d;最大和最小符号距离:dmax,dmin;内群点个数:Nin;点云个数：N;点到当前M的跨度:S;模型评价参数:ω

初始化：ε=0.01，t=1，α′=+，ρ′=0.0

输入：spc

输出：best_M,inliers

1. 计算spc中每个点的权重因子(见1.1小节)；

2. 估计最优模型和内群点集：

whilet>0

利用加权随机采样并估计初始假设模型M;

根据α′确定内群点inliers;

ifNin/N<0.1

t=t-1;

continue;%重新初始化假设模型M

end if

利用最小二乘方法对inliers重新估计M;

计算dmax,dmin,S,Nin,N,α,ρ,其中：α=(max(|dmax|,|dmin|)+mean(|d|))/2.0;

ifρ≥ρ′

ift==1

t=N(N-1)(N-2);

else

end if

best_M=M;

best_inliers=inliers;

best_α=α′;

α′=α;

ρ′=ρ;

else

t=t-1;

end if

end while

1.1 加权采样

传统RANSAC算法中每次采样都具有独立随机性，且所有样本都被等概率采样。然而，在噪声多于内群点时，内群点被采样的概率明显会低于噪声，这就会无法估计出良好的初始模型。内群点平均点密度或内群点数不会在很大程度上小于噪声，反之，噪声就会被认定为内群点，原始内群点被看作是噪声。本文首先通过统计每个目标点pobj的k个最近邻点(k=1用于所有试验)，记为：ψ={p1,p2,…,pk}，并计算k个最近邻点到pobj之间的欧几里得距离，记为：η={η1,η2,…,ηk}，其中ηi=‖pi-pobj‖,i∈1,2,…,k，然后计算邻域半径r=median(η)，最后，遍历整个数据集，统计Ω={r1,r2,…,rN}，N为点云总个数，计算搜索半径R=mean(Ω)，并统计所有目标点在搜索半径R范围内的邻域点个数，将其作为目标点权重因子w={w1,w2,…,wN}，保证在每次迭代中估计初始模型参数时，能够最大可能地在内群点中选取最小样本，降低时间代价。另外， 为了提高权重因子统计的效率，k-d树被用于最近邻搜索和范围邻域点个数的统计过程。

搜索半径R通过影响权重因子w，使得采样样本有更大的概率来自于内群点。但是，如果R过大，每个点的权重差异性就会相对减弱，如果R过小，对于误差较小的噪声作用不明显。而对于不含噪声的数据而言，最近邻点数k对搜索半径R的影响较小，即：R对k不敏感，k可以在较大的阈值范围内取值。为了减弱噪声对搜索半径R的影响，本文引入互为最近邻方法抑制噪声，其原理是最近邻点落在目标点搜索的范围内，同时目标点也落在k个最近邻点的邻域范围内，如图2所示，蓝色实心圆圈不在目标点的最近邻范围内，而绿色实心圆圈落在了蓝色实心圆圈的最近邻范围内。

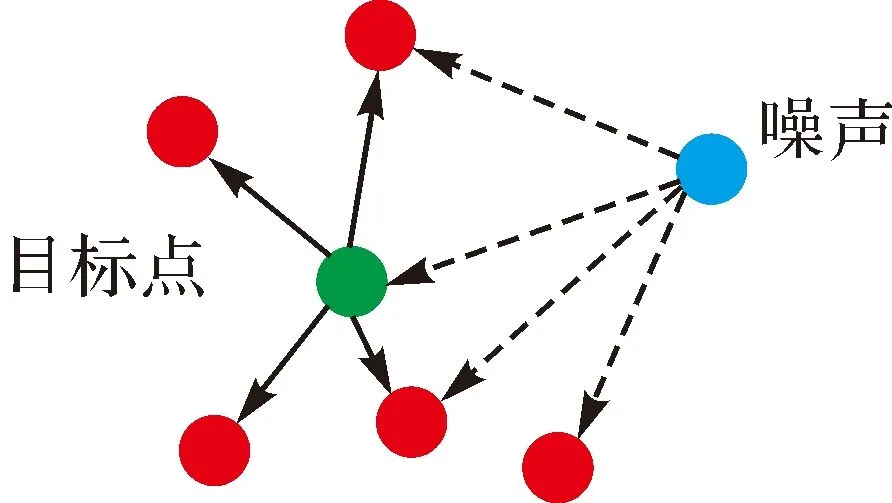
注：绿色实心圆圈为目标点，蓝色实心圆圈为噪声点，实线指向目标点邻域点，虚线指向噪声点邻域点。

1.2 空间密度函数

当场景尺度未知时，误差容忍阈值无法通过人工给定的方式保证高精度估计模型参数，但是，一般情形下，内群点比率与误差容忍阈值往往存在相关性，其适用于不同场景模型。

以平面为例(下同)，假设数据集在容忍误差内没有噪声，其表现为更加紧凑，跨度S将会较小(图3(a))，因此，在最优平面(图3的红色平面)投影面积一定的情况下，每个点的占有平均体积较小。而在图3(b)中，由于存在噪声且噪声往往分布较为分散，跨度S的增加使得每个点占有的平均体积明显增加。另外，噪声还有一个明显的特征是相较于内群点，其偏离最优平面的距离较大。

注:红色平面表示最优平面，绿色立方体盒子表示数据集包围盒，S表示点到最优平面的距离跨度。

令平面P的方程如式(1)

Ax+By+Cz+D=0

(1)

(2)

式中，S=max(dmax,dmax-dmin)表示每一次迭代的距离跨度；max(*,*)表示两者中最大者；S′表示原始数据的距离跨度。由式(2)可知：ρ与S成反比，与Nin成正比。如果减少或增加某个点时，ρ出现明显的变化，则说明点是噪声的可能性较大，反之，ρ基本无变化，则说明点在容忍误差阈值范围内。

1.3 终止条件

对于迭代性回归问题，终止条件对于算法精度和运行效率都非常重要。冗余迭代将会带来较高的时间代价，而迭代不足将可能会导致精度较低。因而，针对不同尺度的场景，自适应的终止条件能够保证在时间成本低的情况下，有效估计出模型参数。

传统RANSAC算法提出一种概率估计的方法计算迭代次数，其假设在真实误差容忍阈值αt范围内，迭代次数为t，则期望E(t)=γ-m，其中，m为最小采样样本。同时，令容忍失败率为ε时，通过式(3)对迭代次数t进行了保守估计

(3)

但是，γ是作为后验知识计算得到的，即：γ与α具有正相关性。已知α为人工给定的误差容忍阈值，β表示最优估计内群点比率，则在足够多的迭代次数时，满足式(4)

(4)

由此可以看出，在传统RANSAC算法中，模型参数估计精度依赖于α的人工给定精度，并且无法通过增加迭代次数t的方式减少α的误差。

为了权衡效率与精度，本文利用空间密度估计迭代次数t，式(5)

(5)

2 试验分析与应用

2.1 试验数据

为了验证方法的稳健性，本文模拟仿真了不同内群点比例的点云数据，用于平面拟合。试验数据采用正态分布与均匀分布伪随机函数分别生成100个内群点和不同比例的噪声。其中，内群点服从

(6)

式中，σ取为1.0。噪声通过随机数方式确定分布在平面两侧的点个数，其坐标服从

(7)

式中，γ分别取为0.1～0.9。另外，本文对每个算法运行1000次，取其平均值用于对比与分析。

在点云拼接或定向中，人工标靶(如平面标靶、球形标靶)常被用作拼接不同扫描站或提供控制点，标靶几何中心精度将会直接影响点云拼接或定向的精度[25-27]。为了验证方法在真实场景中的可行性，本文选取球形标靶作为研究对象，对其表面点云进行球面拟合，并通过点云定向精度对本文算法进行试验对比分析。试验数据使用Rigel VZ-400扫描仪进行采集，一共有11个自制球形标靶，其半径有0.161 m和0.106 m两种。球形标靶中心到扫描仪中心最远距离为78.688 m，最近距离为4.051 m。球形标靶中心的工程指定坐标系采用CGCS2000坐标系，高程采用85高程基准，其坐标见表1的第2—4列。

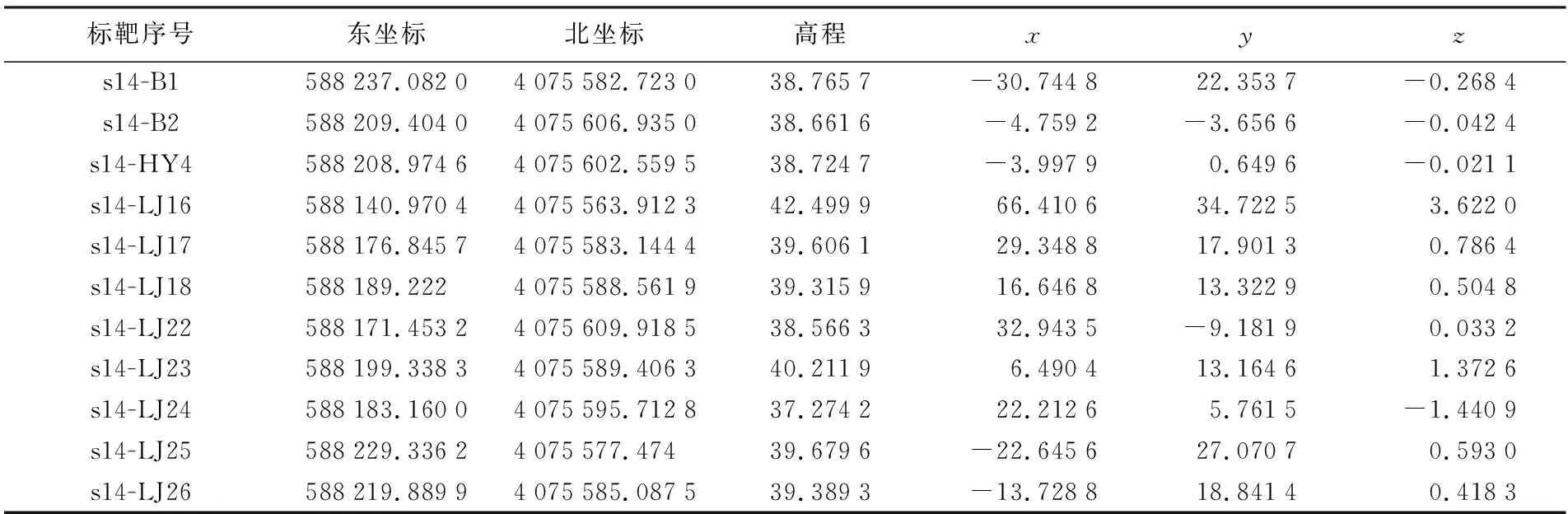
表1 球形标靶中心在CGCS2000坐标系和扫描仪坐标系的坐标

2.2 试验对比

本文分别在查全率、查准率、模型参数误差(见式(8))和迭代次数4个方面与现有算法(MLESAC[12]、RMLESAC[19]、AMLESAC[20]、u-MLESAC[21]和StaRSac[23])进行对比分析

(8)

式中，nin和nout分别为召回的内群点和噪声点个数；Nin为真实内群点个数；p为内群点齐次坐标；M为模型参数；|*,*|表示到M的欧几里得距离。

如图4(a)所示，本文方法的查全率随着γ的增加呈下降趋势，其中，在γ=0.7时，查全率最低，为0.59，并且在γ>0.5时，所有方法中表现最差。但是，本文方法的查准率(图4(b))对于所有γ优于其他方法，尤其是在γ>0.5时，查准率接近于1。u-MLESAC与AMLESAC算法在区分内群点和噪声方面表现最差。在γ<0.7时，查准率较低，尤其γ<0.4时，查准率与γ相同，即：算法无法剔除掉噪声点。

如图4(c)所示，对于所有γ，本文方法的模型参数精度优于AMLESAC、MLESAC和RMLESAC算法，在γ≥0.3时，整体上要优于u-MLESAC和StaRSac算法。需要说明的是，真实值是首先通过100个内群点利用最小二乘估计方法拟合出最优模型参数，然后计算模型参数误差所得。

在时间成本方面，由于AMLESAC、MLESAC和RMLESAC算法的迭代次数是采用默认固定值，其迭代次数不变(如图4(d)所示)，且AMLESAC与MLESAC算法迭代次数相同。对于所有γ，本文方法迭代次数与StaRSac算法接近。为权衡算法精度与效率，u-MLESAC算法的误差容忍阈值选取为5，迭代次数随着γ的减少而逐渐增加，尤其γ<0.7时，迭代次数明显增加。

图4 不同内群点比率(γ)的4项指标对比Fig.4 The comparison between four indicators for the different γ

2.3 在点云定向中的应用

球形标靶凭借其简单、易用、精度高等优势，广泛应用于大场景三维激光扫描点云定向。为了减弱球形标靶表面噪声对点云定向精度的影响，本节首先利用本文方法、u-MLESAC、AMLESAC、MLESAC和RMLESAC算法分别对不同噪声比例的球形标靶表面点云进行定性分析，然后，根据内群点对球形标靶进行球面拟合(本文方法拟合得到的扫描仪坐标系中球形标靶中心坐标列于表1的第5—7列)，通过评定点云定向精度的方式进行定量分析。如图5所示，试验中球形标靶点云密度分布服从文中标靶表面点云密度大于其他位置。

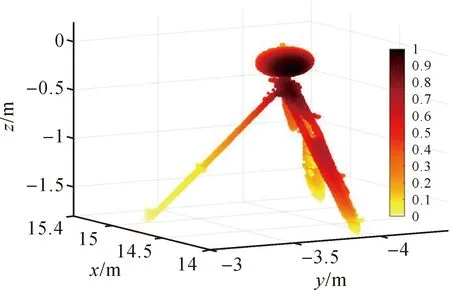
图5 点云密度分布热图Fig.5 The heat map of point clouds density:the darker the color,the larger the density

2.3.1 定性分析

如图6所示，本文方法能够剔除γ≥0.3点云中的噪声(三脚架和底座)，当γ≥0.5时，AMLESAC和MLESAC算法表现与本文方法基本一致，但是，γ=0.3时，算法失败。u-MLESAC算法能够剔除γ≥0.7时的噪声，而RMLESAC算法无法剔除底座处的点云。需要说明的是，StaRSac算法稳健性较差，并且，对于数据量较大的点云，效率太低，没有用于对比试验。本文方法对于内群点(球形标靶)密度大于噪声(三脚架和底座)密度时，对γ有较好的稳健性，而其他方法对于γ更为敏感，即：γ<0.5，算法往往会失败。需要说明的是，图6中的γ取值是一个粗略估计值，只用于定性分析。

注：绿色表示筛选出的内群点，红色表示剔除的噪声，黑色表示整个三角架的点云数据，用于可视化。理想值是球形标靶表面点云。

2.3.2 定量分析

本节首先利用球形标靶中心分别在工程指定坐标系与扫描坐标系的坐标进行坐标转换，统计空间位置残差如式(9)所示

(9)

式中，Err3d表示空间位置误差；Errx、Erry和Errz分别为3个坐标轴误差，然后与现有方法进行对比分析。其中，“人工去噪”是人工交互删除噪声后，使用最小二乘估计法拟合球形标靶中心坐标，然后统计空间位置残差所得。如图7所示，本文方法的空间位置误差整体上明显低于现有算法及人工去噪后拟合计算的中心位置误差，尤其是第5、9、10和11个标靶都在1.0 cm以内，u-MLESAC算法精度最低，误差都在2.0 cm以上。

图7 空间位置误差分析Fig.7 The result analysis of spatial position error

综上所述，在定量分析中，所有方法都可以对噪声进行不同程度的剔除，尤其是本文方法、AMLESAC和MLESAC算法能够剔除γ≥0.5时的噪声。但是，球形标靶表面附近的噪声点对球面拟合精度也会有较大影响。从定性分析结果可以看出：本文方法拟合得到的标靶中心能够更好地用于点云定向，其精度优于现有方法。

3 总 结

本文利用内群点与噪声之间密度差异性提出了一种参数自适应的RANSAC算法，主要解决了传统RANSAC算法及其改进版本需要先验知识的不足，能够适用于不同尺度的模型回归问题。本文首先利用加权采样的方式优化初始模型参数，然后借助空间密度函数来评定最优估计模型，并更新迭代次数和误差容忍阈值，无须任何先验知识。

本文针对不同内群点比率的数据与已有算法分别在查全率、查准率、模型参数误差及迭代次数4个方面进行了详细的对比和分析。在查准率和模型估计精度方面，本文方法明显优于其他算法，适用于图像拼接、几何元素参数估计以及机器人精准定位等对精度要求较高的领域；但是，由于内群点查全率较低，本文方法不适用于几何细节修复等领域。