机载LiDAR数据提取堤防工程特征信息圆环探测法

2021-03-10沈定涛钱天陆陈蓓青王结臣

测绘学报 2021年2期

沈定涛，钱天陆，夏煜，陈蓓青，张煜，王结臣

1. 长江水利委员会长江科学院流域水资源与生态环境科学湖北省重点实验室, 湖北武汉 430010; 2. 南京大学地理与海洋科学学院江苏省地理信息技术重点实验室, 自然资源部国土卫星遥感应用重点实验室, 江苏南京 210023; 3. 长江水利委员会长江科学院空间信息技术应用研究所, 湖北武汉 430010

洪水灾害是最严重的自然灾害之一，全球每年都因洪水事件造成大量的人员伤亡和财产损失[1]。堤防是抵御洪水危害的重要工程措施，近几十年来，通过大规模的堤防建设，我国已建成堤防总长度达到20余万km，在历次抗洪中发挥了巨大的作用[2]。堤防通常由两部分组成，即堤顶和堤坡，其中堤顶是指堤防顶部的平坦表面，其横向宽度比堤基窄，堤坡是指堤防的两侧部分，其外边缘与地面持平，堤坡与堤顶组成堤身。堤防一侧通常是临水的，以抵御洪水侵袭，另一侧为人类活动区域[3]。堤防的规格、形制如堤防最小高程、堤顶宽度、堤坡坡度等都有一套设计规范，我国于2013年发布的《堤防工程设计规范》即明确规定了不同等级堤防的建设标准[2]。

对堤防开展定期巡检，提取堤防工程特征要素是加强洪水保护的一项重要工作。堤防要素包括堤防中心线、堤顶、堤坡、断面线等参数[4]，这些数据是开展堤防工程信息化[5-6]、堤防安全评估[7-9]的重要数据源。传统的使用GNSS技术开展堤防巡检需要到堤防现场对堤防上各个特征点位的经纬度和高程进行测绘，这项工作相当耗时费力，且对技术人员的工程经验要求很高[10-14]。机载LiDAR技术的快速发展为大范围、高精度的堤防巡检工作提供了便利。使用机载LiDAR点云生成的高分辨率DTM与GNSS测绘得到的点坐标不同，它提供的是连续的地表形态数据，基于DTM可以生成各种高精度数据产品[15-18]，如坡度图、曲率图、等值线、断面线等。

研究人员尝试将机载LiDAR数据用于堤防的研究，如堤防制图[19]，堤顶断面提取[20]，堤防中心线提取[21]，堤顶堤坡矢量边界线提取[22-23],堤防侵蚀及稳定性分析[3]等，但这些方法大多对堤防数据完整性要求较高[3]，一些研究需要大量繁杂的人工辅助操作[21,24]。以堤防中心线提取为例，其基本思路是沿着堤防方向，找出一组相邻DTM网格中心点连接而成的矢量线，且要求DTM网格数目尽可能少，而网格高程值尽可能大[21]。最小成本路径分析法是较常见的一种堤防中心线提取方法[20,25]，该方法在堤防两端设置起始点和终止点，以堤防高程为特征计算栅格成本距离，再沿着堤防方向在堤防起点和终止点之间基于成本路径分析查找堤防最高高程点集合，得出起始点和终止点之间的最优栅格路径。最小成本路径分析法较为简便快捷，但其缺点同样明显：一是由于该方法是一种穷举算法，计算效率较低，对计算机配置要求较高；二是一旦堤防存在破坏出现凹凸不平现象，将导致提取的栅格路径出现“毛刺”现象，需要进行后处理平滑曲线。为此，文献[21]又提出了矩阵法、垂线法和点匹配垂线法用于堤防中心线提取。在矩阵法中，通过横向和纵向扫描DTM网格，提取行(列)高程值最大栅格单元，组成堤防中心线。该方法计算效率较高，只用完成两次扫描即可提取所有栅格点，但是其仍存在诸多缺陷，一旦堤防存在蜿蜒曲折，一次横向和纵向扫描会多次穿过堤防堤顶区域，导致漏掉部分栅格点，同时，对于近乎水平或垂直的堤防区域提取效果较差。在垂线法中，通过事先在堤防单侧设置等间隔特征点，从特征点对堤防纵向画垂直射线，统计射线穿过DTM中的最大高程所在的栅格，该方法仍难以避免射线多次穿过堤防堤顶区域的问题。点匹配垂线法对其进行了改进，通过人工在堤防两侧设置数目相同的等间距特征点，特征点之间两两组合构建穿过堤防的垂线，通过垂线与堤防相交统计高程值最高的栅格构建中心线。垂线法和点匹配垂线法需要开展大量的前处理操作，如特征点选取、垂线生成等，工作量较大。

基于上述原因，本文使用机载LiDAR生成的DTM，尝试对堤防中心线、堤顶堤坡形态和堤防断面提取分别开展研究，并提出一整套的技术和方法。最后，将本文方法在洞庭湖区共双茶垸蓄滞洪区堤防开展实际应用，验证所提出方法的有效性，这对加强堤防保护，防范洪水风险具有很实际的应用意义。

1 研究区和数据

洞庭湖位于长江流域中游，是长江最重要的洪水调蓄湖泊(图1)。洞庭湖区经过20世纪50年代堤垸建设、60年代电排站建设以及70年代防洪配套治理工程建设，目前已形成大小堤垸226个，防洪大堤总长度5812 km。洞庭湖区堤防建有水闸、涵管5000多处，电排站3000多座，这些穿堤设施大多修建于20世纪50、60年代，老化严重，运行不良，对堤防安全构成严重威胁，防汛任务巨大。本文研究区共双茶垸蓄滞洪区防洪干堤为一闭合环形结构(图2)，总长度120.1 km。共双茶垸蓄滞洪区位于沅江市北部，北临草尾河，南临黄土包河，东面南洞庭湖、西面隔水与赤山相望，四面环水，为洞庭湖区24个大型蓄滞洪区之一。

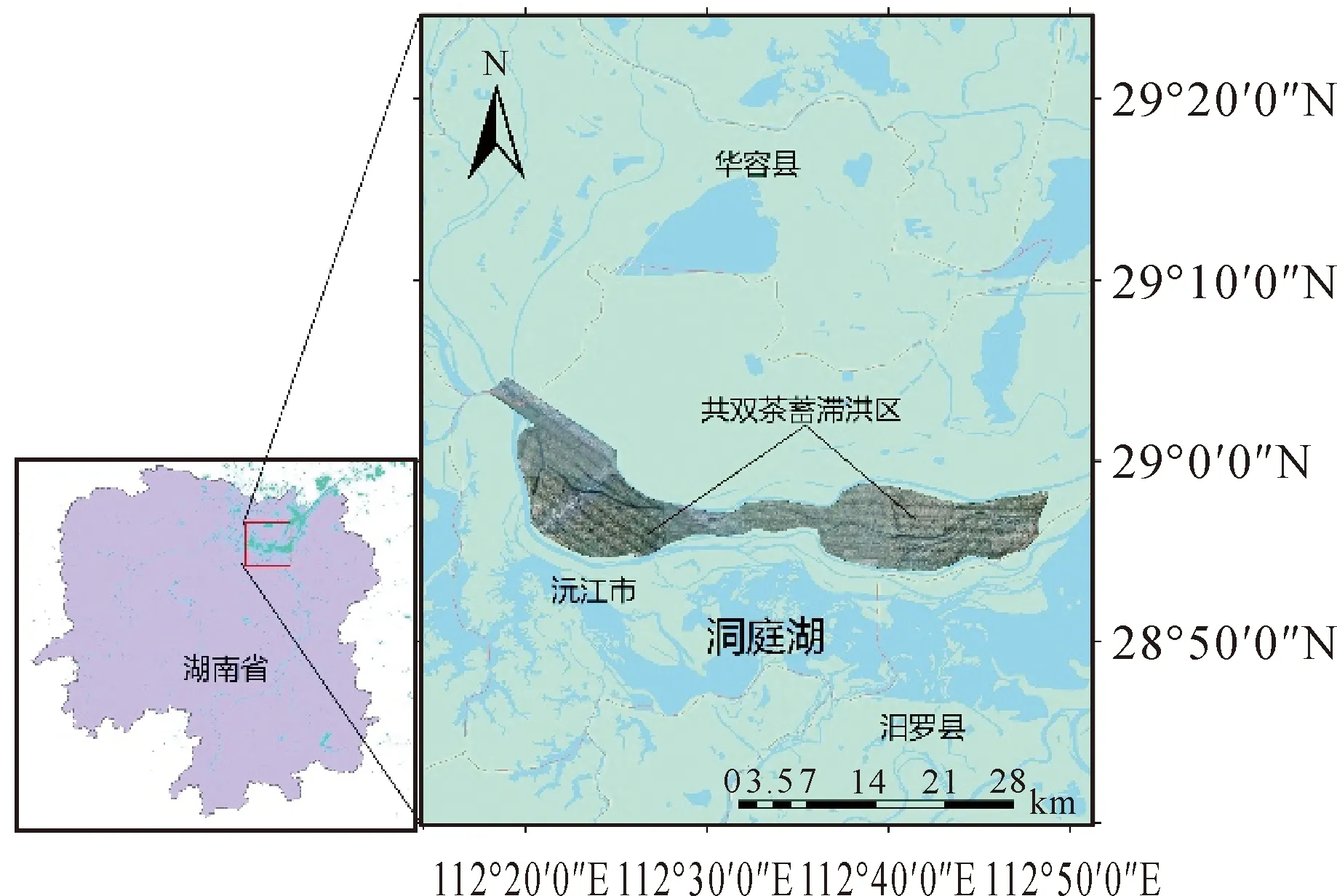
图1 共双茶垸蓄滞洪区在洞庭湖区的位置Fig.1 The location of the Gongshuangcha detention basin in the Dongting Lake area

本文使用德国TopoSys公司HARRIER 68i机载激光测量系统对共双茶垸开展了航空摄影测量工作。机载激光测量系统中数码相机使用的是Trimble公司的Rollei Metric AIC Pro(像素6000万)；惯导系统型号为Applanix POS/AV系列，采样频率200 Hz；激光扫描仪的型号为Riegl LMS-Q680i，最大脉冲频率80 KHz～400 KHz，扫描角度45°/60°。通过对采集的机载LiDAR点云进行处理，生成了1 m高分辨率堤防DTM数据(图2)，平面位置中误差为0.44 m，高程中误差为0.04 m。

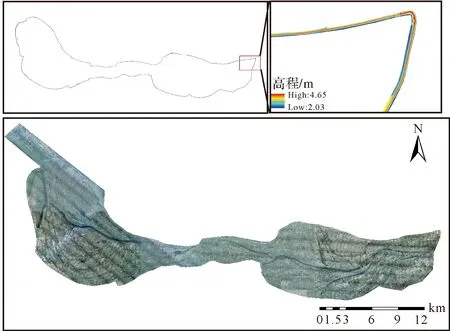
图2 蓄滞洪区影像及堤防DTM数据Fig.2 Image of flood detention basin and DTM data of levee

2 特征信息提取方法

2.1 堤防中心线提取

2.1.1 圆环探测法基本原理

现有堤防中心线自动提取方法对堤防形态完整性要求较高，然而堤防通常会受到不同程度的破坏，使得堤防形态发生变化，堤防中心线提取难以获得较满意的效果。如图3所示，以本文研究区为例，堤防受到洪水侵蚀、工程建设等的影响，很难将上述方法用于本文研究区堤防中心线的自动提取。

图3 由于人类活动、侵蚀等造成堤防破坏Fig.3 Levee damage due to human activities, erosion, etc

图4是一段堤防示意图，堤顶区域高程较堤坡区域高，堤防中心线即是要从堤顶区域提取高程值最大的系列栅格点。如图5所示，堤防“中间高，两侧低”的形态特征使得DTM中间区域网格高程高于边缘区。假定以一圆环覆盖于堤防上，并探测圆环穿过的所有DTM网格高程，查找高程值最大的栅格，基于堤防形态特征，可以确定该栅格单元是属于图5位于堤顶区域的红色栅格。

图4 堤防示意图Fig.4 Levee diagram

图5 圆环与堤防DTM相交计算Fig.5 Intersection of ring and levee DTM

如图6所示，若将查找到的DTM栅格中心(B点)作为圆心点绘制新的圆环，该圆环与圆环A相交，那么可以在位于圆环A外部的圆环B上，查到高程值最大的栅格，该网格中心为点C处于堤顶区域。以此类推，在堤防DTM上查找高程值最大的栅格，依次连接栅格中心点A、B、C、D、E等形成的矢量线，即是堤防中心线，可以将此方法称为圆环探测法。

图6 圆环探测堤防DTM高点Fig.6 Ring detection of high point on levee DTM

2.1.2 中心线提取方法

因为堤防平均宽度w可以看作是已知的，圆环半径r的设定则相当重要。半径r过小，会出现圆环完全处于堤防DTM内部，或者圆环只与堤防一侧相交，此时可能选不到堤防中心线上的点，也可能出现圆环之间形成“回路”，即新圆环与之前的圆环相交，导致计算失败。若半径r过大，在堤防大幅变向处，圆环探测会漏掉堤防拐弯处的“尖点”。因此，有必要分析堤防平均宽度w与圆环半径r的关系，以尽量规避上述情形，进而实现堤防中心线的自动提取。

(1) 确定圆环半径r。设定堤防平均宽度为w，则圆环半径r必须满足如下条件才能获得满意的计算效果

(1)

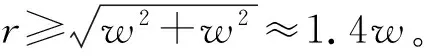
图7 圆环半径r设定Fig.7 Ring Radius r setting

(2) 确定圆环离散点n。假定当前圆环中心O点的坐标(xo,yo)，圆环半径r，DTM栅格单元宽度为c。若将圆环离散化为一系列圆上点集，只要点足够密集，就可以通过圆上点查找高程值最大的栅格。为避免漏掉圆环穿过的栅格，必须使得圆上相邻离散点距离不超过一个栅格宽，则相邻离散点的距离l需满足l≤c，又已知圆环周长为2πr，若将圆环n等分，则圆环上相邻离散点的距离l≈2πr/n，即必须满足2πr/n≤c，进而可推导出n≥2πr/c。以本文研究区为例，DTM网格宽度c=1 m，圆环半径r=50 m，则n≥314。为便于计算，将圆环360°等分，即n=360，此时圆环上相邻离散点之间距离l≈2πr/n=0.87 m，完全满足圆环探测需要。

如图8所示，以圆环中心点O为坐标原点，以水平方向为x轴，垂直方向为y轴，从x轴正方向上作为圆环第一个点开始，依次按照1度递增，形成圆环点集，共计360个点。那么，对点集中的A点而言，其与x轴正方向的角度α是已知的，设圆环中心O点的坐标为(xo,yo)，则点A的空间坐标xA，yA满足式(2)

图8 求堤防中心线上点A坐标Fig.8 Calculate the coordinate of point A on the central line of levee

(2)

由于DTM网格宽度为c，假设DTM范围最小最大坐标为(xmin,ymin)、(xmax,ymax)，则点A对应的DTM网格行列号IA，JA满足式(3)

(3)

按照式(2)和式(3)，查找圆O上所有离散点，找到高程值最大的点。如图8所示，假定点A所在的DTM网格就是高程值最高网格，以点A为圆心，r为半径做圆，因为圆心点A所在的圆和圆心点O所在的圆半径都是r，则点A所在的圆必过点O。假定圆A和圆O相交于点P1和点P2，线段AO和线段P1P2相交于点P。要找到圆A上的某一堤防中心线上点B，则点B必须满足式(4)

(4)

按照上述计算方法，依次得到所有堤防中心点，生成堤防中心线。

2.2 堤防形态参数提取

堤防监测包括对堤防形态参数进行长期观测，如堤防高度、堤顶、堤基宽度、坡度等，这些参数通常是使用GNSS测量获得。堤防上每隔一定距离需要采集堤防断面数据，断面处通常是由断面点构成，这些断面点的间隔距离设定非常依赖于观测人员的经验[12-14]。基于LiDAR数据提取的DTM数据有着较高的数据精度，用于堤防形态参数提取有着更好的效果，同时可以从堤顶和堤坡矢量面数据提取堤防轮廓线数据。

2.2.1 堤防堤顶、堤坡提取

获取堤防每一区域的堤顶和堤坡参数信息是进行堤防破损检测的重要基础。按照《堤防工程设计规范》国家标准的规定，对土堤堤防而言，“1级堤防堤顶宽度不宜小于8 m，2级堤防堤顶宽度不宜小于6 m，3级堤防堤顶宽度不宜小于3 m；堤顶的坡度应向一侧或两侧倾斜，坡度宜采用2%～3%；1级、2级土堤的堤坡不宜陡于1∶3”(即坡度为18.43°)[2]。

基于堤防坡度区分堤顶和堤坡是较为常见的方式，如文献[24]的研究中，堤防顶部坡度值范围设定为[0°,8.43°]，堤坡坡度范围设定为[8.43°,43.69°]。共双茶垸蓄滞洪区主干堤防为3级堤防，由于该堤防建设时间较早，而《堤防工程设计规范》国家标准于2013年颁布，因此共双茶垸蓄滞洪区干堤并不能完全满足该标准对3级堤防的要求。按照国家标注对1级、2级堤防堤坡不陡于18.43°的规定，参照文献[24]的研究将本堤防堤坡的坡度值容许加减±10°的误差，即堤坡坡度为[8.43°,28.43°]，同理，国家标准对堤顶的坡度要求为2%～3%，此处考虑堤防的建设现状，将堤防堤顶坡度设定为[0°,8.43°]之间。

提取堤顶和堤坡形态参数的第1步即是将堤防DTM数据生成坡度图，如图9(a)所示。该坡度图中最大坡度为68.87°，最小坡度为0°。按照上述对堤顶和堤坡的坡度范围分析，将坡度图中坡度分为3类：[0°,8.43°]、[8.43°,28.43°]和[28.43°,68.87°]，得到的坡度分类图如图9(b)所示。

最后，将坡度分类图矢量化，得到坡度分类图矢量数据，如图9(c)所示。图9中出现了较多的碎图斑，这些碎图斑面积一般小于100 m2(10 m×10 m)，多数是因为堤顶和堤坡上由于多年侵蚀和人工建设造成，使用ArcGIS的eliminate工具，将那些面积较大的图斑内部面积低于100 m2碎图斑融合到大图斑中，得到结果如图9(d)所示。

因为在裁剪堤防DTM的过程中，堤防外侧一些农田等非堤防区域也包含在了堤防DTM中，在生成坡度图时，这些区域的坡度也涵盖在[0°,8.43°]、[8.43°,28.43°]坡度范围中。如图9所示，在局部放大图中，位于堤防外侧的品红色图斑与堤顶图斑都属于坡度范围为[0°,8.43°]，该图斑实际上不是堤顶，是处于堤防外部的农田。因此，针对上述矢量化成果，需要剔除堤防外侧的这类图斑，以及坡度范围为[28.43°,68.87°]的图斑，得到最终包含堤顶和堤坡的堤防形态矢量数据如图9(e)所示。

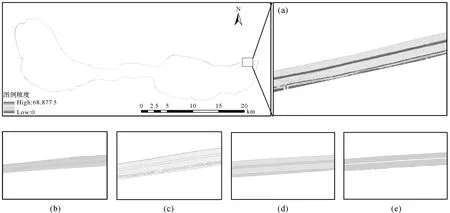
图9 堤防堤顶、堤坡提取Fig.9 Extraction of levee crown and slope

2.2.2 堤防断面线提取

堤防断面数据是堤防工程最重要的特征信息，划分堤防断面，分析断面处的堤防高程变化，可以对堤防横切面形态有更加直观的认识。本文在上述提取堤防中心线过程中按照50 m等间距对堤防划分圆环，可以直接在每个圆环圆心处划分断面。如图10所示，线段MN即是需要自动提取的断面线，该线段是∠OAB的角平分线，M点和N点都位于以A为圆心的圆环上，即线段MN的长度为2r。只要求出点M和点N的空间坐标，即可得到穿过圆心A的断面线MN。

如图10，已知点O、点A和点B的空间坐标分别为(xO,yO)、(xA,yA)、(xB,yB)，因为点M位于圆环A上，且点M到点O和点B的距离相等，即点M满足

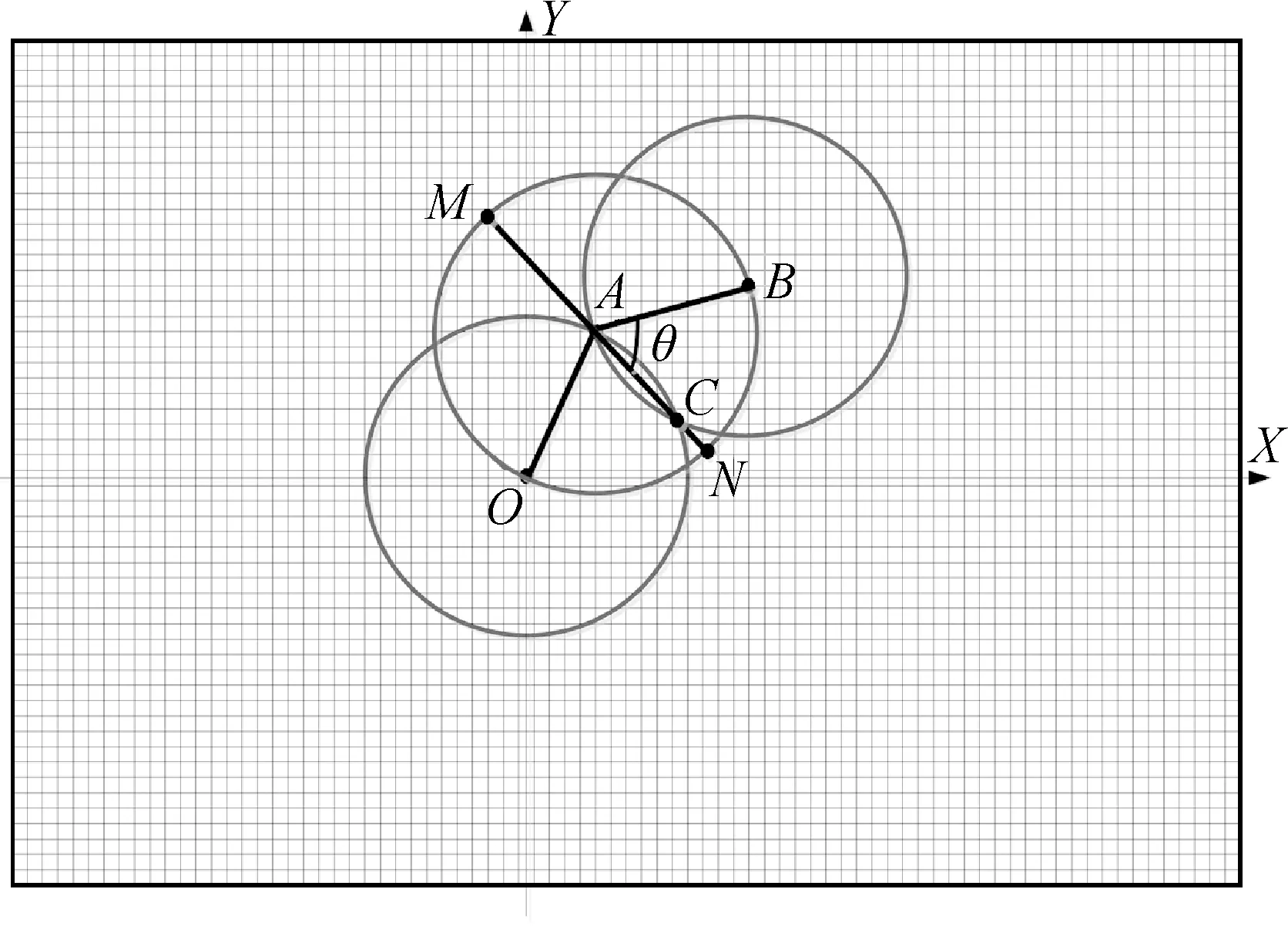
图10 堤防断面线自动提取Fig.10 Automatic extraction of section lines of levee

(5)

按照前述圆环离散化方法，对圆环A上离散点进行遍历，结合式(2)、式(3)、式(5)，必定可以求得点M的坐标，计算点N的坐标同理。对于堤防上任一断面线，探测断面线穿过的堤防DTM网格即可获得断面处堤防高程变化曲线。

3 结果与分析

3.1 堤防中心线结果分析

图11和图12是使用上述方法得到的堤防圆环和堤防中心线数据及其局部放大。与最小成本路径法等逐栅格采样方式相比，本文方法在数据采样精度上存在一定精度损失，但本文方法对堤防形态变化等敏感度较低，针对图3的各类堤防“异常”情形也可以得到较满意的中心线数据。

图11 圆环探测及中心线生成Fig.11 Ring detection and centerline generation

图12 中心线局部放大Fig.12 Magnification of centerline

本文提出的圆环探测法有效规避了各种堤防异常问题，如图13所示，堤防由于破损等情形的存在导致DTM中网格高程异常。其中的暗色斑点属于异常高程点，这对如矩阵法、最小成本路径法等逐栅格提取中心线的方法易使得计算结果效果较差。本文方法在堤防上间隔采样，可以在一定程度上避开这些局部高程异常的网格，尽量保证堤防中心线处于堤防纵向中心位置。在一些堤防破损非常严重的区域，有少数这种高程异常凸起的网格点被采样作为堤防中心线点，这些偏离堤防中心区域的异常点也表明了此处堤防破坏较为严重。

图13 堤防局部高程异常Fig.13 Abnormal elevation of local dike

3.2 堤防堤顶、堤坡结果分析

尽管堤防在正常区域能够提取出正确的堤顶、堤坡形态参数。但是，因为受到水土侵蚀、人类活动等影响，仍然存在部分堤防堤顶和堤坡形态被破坏的情形，如图14所示。在图14(a)中，因为在堤顶存在建筑物，堤防堤顶多边形出现“拐弯”现象，且建筑物区域的坡度也处于堤顶坡度范围，同时导致堤防中心线也出现“拐弯”现象；在图14(b)中，因为人类活动和水土侵蚀，堤顶宽度出现剧烈变化，堤顶过宽或过细，这是堤防缺乏养护的典型表现；而在图14(c)中，由于人类活动对堤防破坏太大，不仅出现堤顶宽度过宽，而且导致堤防中心线变道，堤防在纵向上，出现多条堤顶和堤坡区域。

图14 堤防堤顶、堤坡形态受到破坏Fig.14 Damaged levee crown and slope

3.3 堤防断面结果分析

基于上述求断面线端点坐标式(4)，得到的堤防断面线如图15所示，研究区堤防共生成断面2401个。

图15 堤防断面线提取结果Fig.15 Extraction results of levee section lines

堤防破损对断面高程的影响也不容忽视，在堤防破损比较严重的区域堤顶宽度和堤坡坡度都发生了显著的变化。如图16所示，图(a)为正常堤防区域某断面的高程变化，图(b)为异常堤防区域某断面的高程变化。本文研究区堤防堤顶高程在35 m左右，在正常堤防区域堤顶部分高程值与堤坡高程值有很明显的对比，堤顶宽度也符合堤防设计规范，而在异常堤防区域，由于堤防受到较严重的破坏，导致堤防堤顶区域不明显，整个横断面有一大片区域高程值都达到35 m，导致堤坡窄而陡。

图16 堤防断面高程变化对比Fig.16 Comparison of elevation changes of levee cross section

4 讨论

4.1 与几类堤防中心线生成方法的对比分析

图17是文献[21]提出的堤防中心线生成方法，其中矩阵法是自动算法，垂线法和点匹配垂线法是半自动算法。图17(a)为矩阵法示意图，扫描线EF实际跨越了两个堤防中心线点，但是算法只能提取其中一点，因此对于堤防弯曲较大的区域存在漏掉关键点的可能。同时，当局部堤防区域过于水平或垂直，扫描线很难提取到所有中心线点。如图中扫描线CD几乎与堤防中心线重合，再加上此区域横向扫描存在跨越两次堤防中心线的情形，使得中心线点提取存在困难。

如图17(b)和图17(c)所示，垂线法是在堤防边缘单侧取点，点匹配垂线法是在堤防边缘双侧取点，然后手工绘制垂线，通过垂线与堤防相交查找中心线点。该方法较为烦琐，需要大量的辅助操作，以点匹配垂线法为例，若用于本文研究区堤防中心线提取，假定按照本文研究设定的50 m取点，需要在120 km长的堤防双侧各选取2400个点构建垂线段。

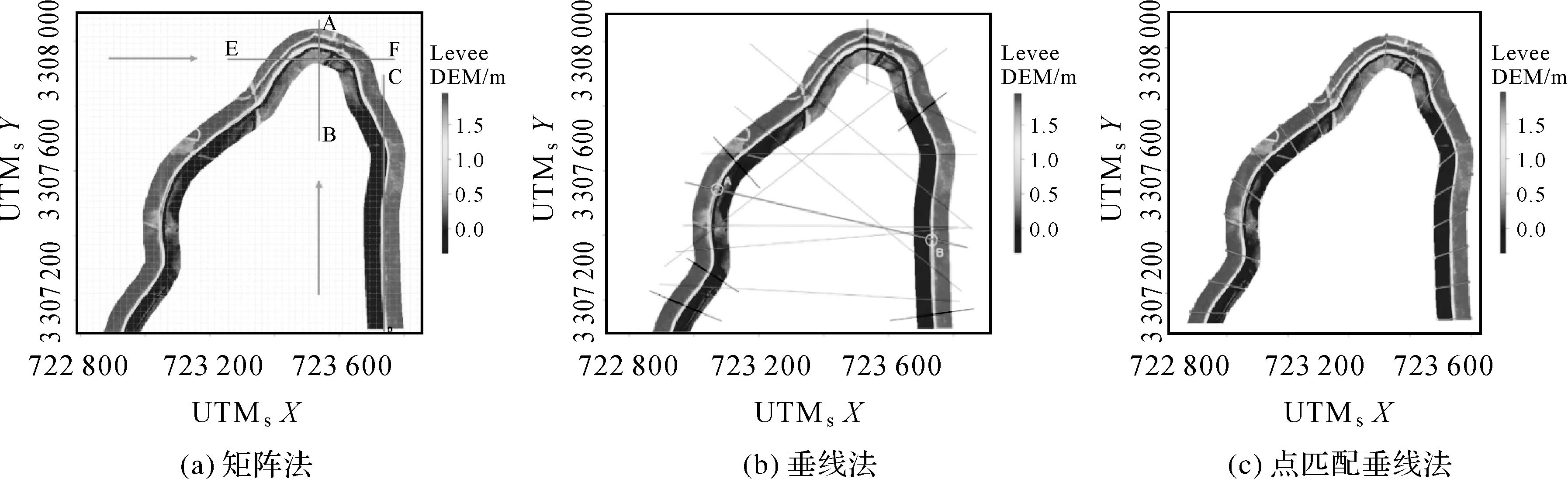
图17 3种堤防中心线生成方法[21]Fig.17 Three generating methods of levee center line[21]

图18和图19分别是使用矩阵法和最小成本路径法对本文研究区堤防数据提取中心线。采用矩阵法提取的最大高程值栅格在空间上很难做到相互连接，若直接执行栅格转换矢量会生成大量断线，因此该方法仍需要大量的后处理操作才能得到满意的堤防中心线数据。使用最小成本路径法获取的堤防中心线虽然没有矩阵法出现的散乱断线问题，但是存在大量的“毛刺”现象，需要进行平滑后处理操作。

图18 矩阵法生成堤防中心线Fig.18 Generation of levee center line by matrix method

图19 最小成本路径法生成堤防中心线Fig.19 Generation of levee center line by cost path analysis

图20为采用最小成本路径法、矩阵法和圆环探测法得到的堤防中心线结果对比。由于最小成本路径法需要计算路径最短、成本最小(高程最高)的栅格集合，因此在堤防弯曲较大的区域，最小成本路径法得到的堤防中心线出现“抄近路”现象而漏掉堤防中心线关键点。由于圆环探测法中最大高程点探测是在圆环上，一旦堤防“尖点”位于圆环内部，则同样存在漏掉关键点的可能。一种有效的解决方法是对圆环进行加密探测，如图21所示，A、B、C为堤防中心线点，由于点A和点C位于圆环B的360个环上点次序是可知的，根据对称性，可以计算得出平分线段AC且穿过点B的圆环上点E、H，进而分别计算得出弧AH、HC、AE和EC的二等分点G、I、D、F。可以类似点匹配垂线法，计算线段GD和线段FI穿过堤防区域的最大高程点，分别统计最大高程点与线段AB和BC的垂直距离，通过预先设定的距离阈值确定是否保留该最大高程点作为堤防中心线，从而可以避免漏掉堤防关键点。

图20 堤防中心线结果对比Fig.20 Comparison of levee center lines

图21 圆环加密探测示意图Fig.21 Schematic diagram of ring encryption detection

4.2 与Bresenham绘圆算法的对比分析

Bresenham绘圆算法是计算机图形学领域的经典算法，该算法是为解决几何图形的计算机显示问题而设计的。本文尝试使用Bresenham绘圆算法提取堤防中心线，并与本文所提出的方法进行对比分析。由于Bresenham绘圆算法是基于“点阵逼近”模拟圆形，确定点阵间距非常重要。为了避免圆环在DTM网格上探测时漏掉栅格，必须保证圆环上相邻点间隔不超过1个网格。本文中DTM网格空间分辨率为1 m，为此将Bresenham绘圆算法点阵间距设置为1 m可以满足上述要求。图22是使用Bresenham绘圆算法绘制的半径为50 m的圆形，共288个点。与Bresenham绘圆算法不同，本文所使用的圆环绘制方法属于“多边形逼近”方式绘圆，多边形有360个点均匀分布在圆上。同时，Bresenham绘圆算法特点使得各点位于圆环内侧或外侧，并不完全位于圆上，如图22红色圆弧所示，“多边形逼近”绘圆效果明显好于“点阵逼近”绘圆效果。

图22 两种绘圆算法对比Fig.22 Comparison of two circle drawing algorithms

设定DTM网格宽度为c，堤防长度为L，圆环半径为r，可知圆环探测法所需圆环数量约为L/r，按照前述分析，圆环离散点n=2πr/c，则本文研究所采用的圆环探测法算法时间复杂度为T(n)=nL/r=2πL/c，即算法时间复杂度是关于堤防长度与DTM网格宽度比值的一个线性函数。受圆环相邻点间隔必须控制在一个网格距离的约束，本文所采用的绘圆方法和Bresenham绘圆算法二者所需的圆环点数量比可以近似看作是一个常数，因此，两种绘圆方法的时间复杂度是一致的。

图23是两种绘圆方法提取堤防中心线的局部结果对比，Bresenham绘圆锯齿状明显。由于两种方法的圆环采样点选取原理不同，使得最大高程点栅格选择会出现一定偏差，导致两种圆环探测结果并不完全重合。本文所采用的圆环绘制方法仅基于圆环中心坐标和半径即可快速计算环上任一点的坐标，且圆环点对称性更好，用于圆环加密探测(图21)和圆环断面提取(图10)时简便快捷，比Bresenham绘圆更便于程序实现。