不同曲度下90°矩形弯管内部流场数值模拟研究
2021-03-09刘天昀徐星宇李晨斌焦慧杰
刘天昀,徐星宇,李晨斌,焦慧杰
不同曲度下90°矩形弯管内部流场数值模拟研究
刘天昀,徐星宇,李晨斌,焦慧杰
(华北电力大学 能源动力与机械工程学院,河北 保定 071003)
为了研究90°矩形弯管在不同曲度下的内部流场情况,以Gambit构建管道模型,使用Fluent软件、采用Standard k-ε模型对=1.05~4.55曲度范围内的矩形管内空气的流动进行了数值模拟计算,分析了管内静压强和速度分布、漩涡产生的部位及强度、局部损失系数以及管道弯曲部分的受力情况,探究了弯管后二次流的持续发展情况以及增加导流板对减小局部损失系数的作用。研究结果表明:随着弯管曲度的增大,进口截面压强下降,局部损失系数降低,流体对弯管的作用力增加,弯管后二次流的影响范围增大;增设导流板后,管内压强和速度分布更为均匀,二次流强度减弱,局部损失大大减小。
矩形截面弯管;曲度;数值模拟;导流板;局部损失系数
管道广泛应用于工业运输、农业灌溉、室内供温等诸多领域。近年来,随着工、农业的迅速发展,管道的应用越来越多,类型也越来也丰富。由于空间、位置等限制,不可避免地要用到各种弯管,如船舶管道、汽车油管、空调制冷管等各种管路中均有弯管的应用[1]。在火电领域,锅炉中的烟道系统、冷却水循环系统与送风系统中更是布满管道[2]。
较直管而言,受漩涡及二次流等因素的影响,弯管内的局部损失系数增大,流动损失增加,影响经济效益,且流体对管道的冲击力、管内压强也增大,更易发生管道破损和流体泄漏事故,危及管道使用寿命及施工安全。因此,优化管道内部流场结构,降低管内压强及流体对管道的冲击力,减少流动损失,对实际工程中延长管道寿命、提高经济效益及保障施工安全具有重要意义。
为增强管道性能,已有学者对弯曲圆管做了诸多研究,但对矩形管的研究相对较少。在前人研究的基础上,本文结合流体力学,采用Fluent数值模拟方法研究空气在不同曲度下的90°矩形管道内的流动情况,避开了实验研究耗费大量人力、物力的缺陷[3],研究工作主要包括Gambit建模和计算、Fluent模拟管内静压和速度分布、漩涡产生的部位及强度,分析了曲度=1.05~4.55范围内进口截面压强、流体对弯管的作用力、二次流的影响范围及局部损失系数的变化情况,探究增加导流板对降低局部损失系数的影响。
1 模型的建立和求解
1.1 几何模型建立
本课题研究的模型如图1所示,管道的横截面是一个边长为400 mm的正方形,直管道部分的长度为6000 mm,弯转角度为90°。弯管的曲度为自变量,分别取1.05、1.55、2.05、2.55、3.05、3.55、4.05、4.55。曲度变化时其它变量保持不变。
图1 弯管模型及几何尺寸
1.2 网格划分
划分网格数量的多少会直接影响计算精度和准确性。网格数目越多,计算精度会越高[4],但计算规模也会增加,计算机的运算负担也就增大,运算所需要的时间也就越长。因此,在确定网格数量时,需要平衡两者,既要满足计算精度要求,又要减轻计算机运算负担[4]。
以=1.05为例,以不同的网格划分数量为变量,以局部损失系数为对比参数进行网格无关性分析。
1.3 网格无关性验证
通过表1可见当网格规模为40万以上时,弯曲管道的局部损失系数相对误差小于2%,因此取40万以上规模的网格进行计算。
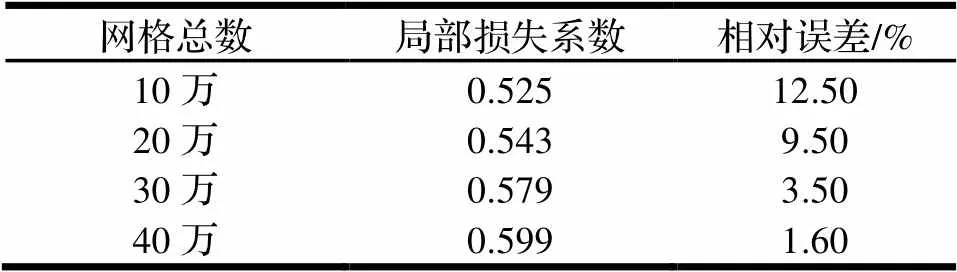
表1 网格总数与局部损失系数的关系
1.4 物理模型构建
本次课题中使用Gambit 2.4.6建模。首先采用由面拉伸为体的方法绘制出曲度分别为1.05、1.55、2.05、2.55、3.05、3.55、4.05、4.55的矩形弯管;然后按照弯管处密集、直管处稀疏的原则进行网格划分,网格数目要达到40万;接着在边界条件的设置中将进口设置为velocity-inlet,出口设置为outflow,弯管壁面设置为wall;最后将构建好的几何模型导入Fluent 15.0。构建好后的模型如图2所示。

图2 导入Fluent后的几何模型
1.5 Fluent求解计算
读入mesh网格文件后对文件进行检查。在本例中,雷诺数在500000左右,该数量级远远大于2300,所以在选取模型时要选取湍流模型。由于在湍流模型中,Standard k-ε模型用途最为广泛,具有收敛速度较快的特点,可以很好地减少计算机的运算量,释放更多CPU。经讨论,最终一致认为Standard k-ε模型是非常合适的,其控制方程组如下:
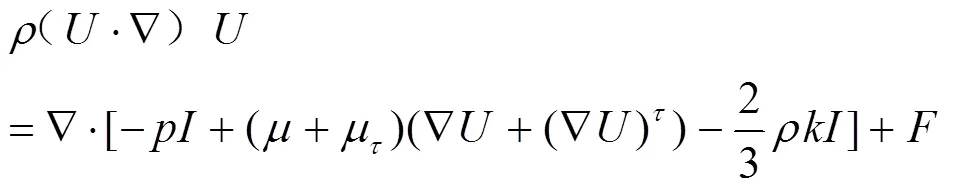
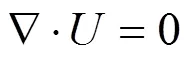
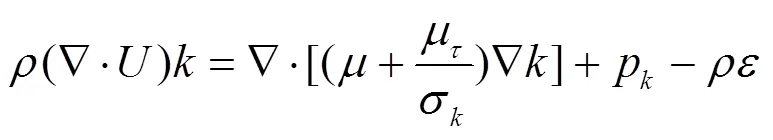
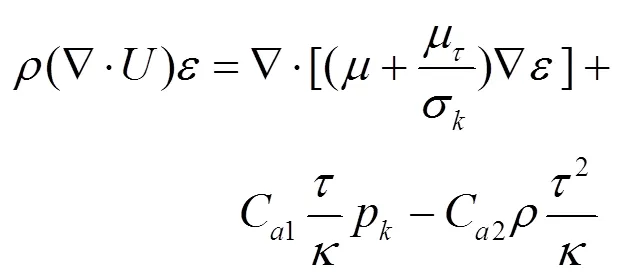

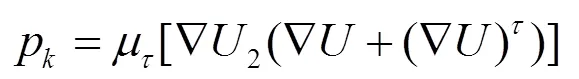
将materials设置为空气,保持其默认参数。然后对边界条件进行了设置,进口设置为速度进口(velocity-inlet),速度大小为15 m/s,湍动度为5%,出口设置为自由出口(outflow),其余参数均为默认设置未作更改,然后再对流场进行初始化。最后进行迭代计算,结果如残差曲线图3所示(以=1.05为例),当残差小于0.0001即步数在145左右时,可以认为计算已经收敛。
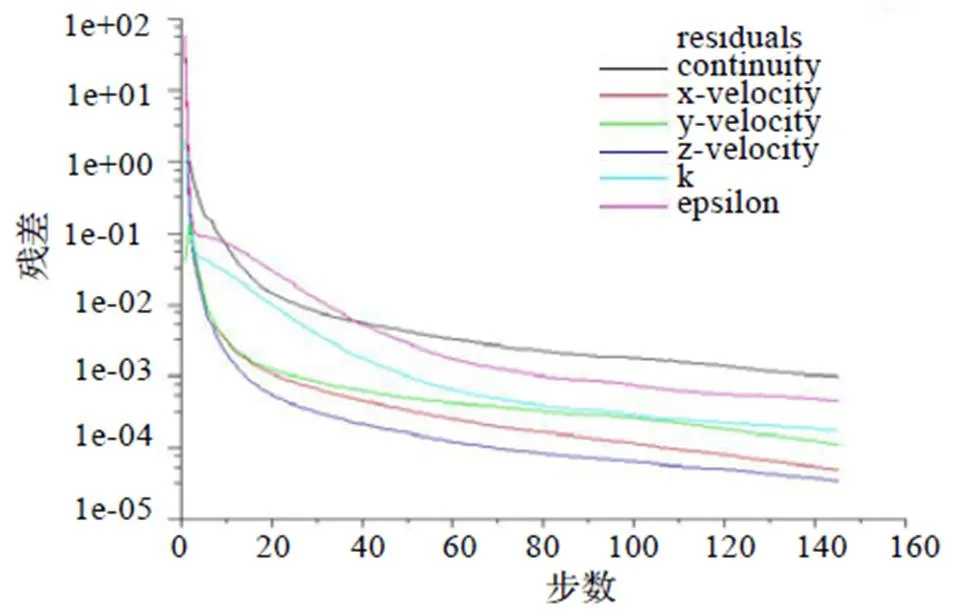
图3 残差曲线图
2 模拟结果分析
2.1 曲度对弯管局部损失系数的影响
2.1.1 局部损失系数的计算


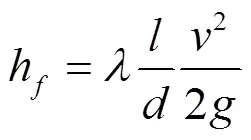
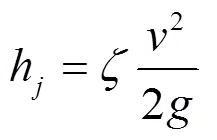

式中:1与2为管道进口与出口截面的平均压强;1与2分别为管道弯曲部分进口与出口截面的平均速度;数值均在Fluent当中读出。
2.1.2 曲度对弯管局部损失系数的影响
通过对比计算得到圆截面弯管的局部损失系数随着曲度增大而逐步减小,经过实验数据(图4)所分析出的矩形截面弯管的局部损失系数也是随着弯管曲度增大而减小。这是因为:当流体流经弯管时,由于流体具有惯性,弯管会使流体的流动方向发生突然的转变,从而导致流体会冲击管壁,并在弯管内经历拥堵、减速、转向、再加速的流动过程,从而导致了流体再弯管处会产生局部损失。
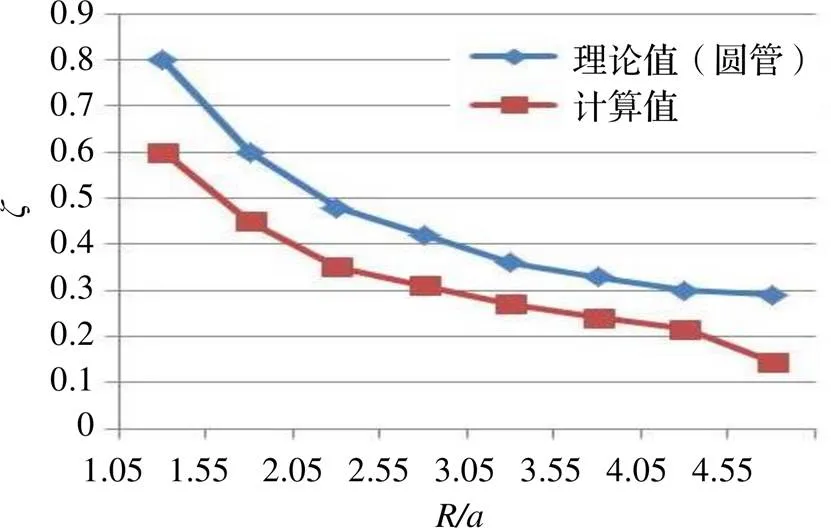
图4 弯管局部损失系数随曲度的变化
当弯管的曲度较小时,弯管的形状可以近似看作是直角弯管,没有了圆弧形弯管的缓冲作用,流体在直角弯管内速度方向急剧改变,从而导致局部损失系数较大。随着弯管的曲度逐渐增大,弯管的弯曲程度逐步减小,流体在流经弯管时流动方向的改变程度也变小,对管壁的冲击碰撞减小,导致流体在流经弯管时流动损失也减小、局部损失系数也随之减小。但随着弯管曲度的进一步增大时局部损失系数并不会持续减小,当达到一定数值时局部损失又会增大。这是因为:虽然弯管弯曲程度变缓,但弯管弯曲部分的长度增长了,流体流经弯管时与管壁的碰撞、摩擦的长度增加了,这又导致了局部损失的再次增大[3]。
综上所述,随着弯管曲度的增大,其局部损失系数呈现先减小后增大的趋势;当曲度较小时,弯管处流体的流动方向的剧烈转变对局部损失系数起主导作用;当曲度较大时,弯管处流体与弯管部分的摩擦对局部损失系数起主导作用。但是这个结论并没有在所研究的曲度范围中体现出来,这可能时由于空气的运动粘度较小且实验的曲度最大值未达到拐点。
2.2 弯管内的静压和速度分布
2.2.1 静压分布(以=1.05为例)
由图5可以看出,从整体分析,静压强是沿着管道流动方向逐步降低的。在管道中,当流体处于进入弯管前的直管道部分与离开弯管的后的直管道部分时,压强分布比较均匀。在弯管处压强变化比较大,分布不均匀。即在弯管的内侧与外侧处发生明显变化。其中,在经过外侧拐点时,压强达到最大值,而当流体流经内弯拐点时压强达最小值,并在弯管的内侧还产生了负压。这说明在弯管的内外侧存在着较为显著的压力差,同时这也是二次流形成的重要原因之一。

图5 弯管静压强分布云图
2.2.2 速度分布(以=1.05为例)
由图6可以看出,先从整体分析,速度是沿着流管内流体的流动方向整体变化不大。但在管道拐弯处,弯管内侧的速度较大,而外侧的速度较低。弯管内侧的流体流过拐弯处时,由于该侧压强较低,受到后面流体的冲挤,导致速度增大。当流体流过拐弯处进入直管段后,流动迅速发展为充分发展状态,沿管道截面,速度分布趋于均匀。但是因为流体流动过程有一定流动损失,因此速度与流入拐弯处前的相比略微有所下降,但变化不大。弯管外侧的流体流动过程分析与内侧类似。

图6 弯管速度分布云图
对比图5与图6可以发现,速度的分布恰好与压强的分布相反,即在流体经过外侧弯管时其速度达到最小值,而在流体流经内侧弯管时其速度达到最大值。
2.3 管内漩涡产生的部位及强度
在流体流经弯管时,在贴近弯管壁面处会产生漩涡。在弯管内侧,产生漩涡的原因是流体流经弯管时由于具有惯性,同时在弯管内侧出口段进入直管段这部分区域是逆压梯度区,极易发生边界层分离,因此流体边界层脱离内壁,并在壁面附近形成了与主流方向相反的回流,最终形成漩涡;而在弯管外侧,产生漩涡的原因是流体改变流动方向时,冲刷撞击外壁面,同样导致了与主流方向相反的回流产生,最终也形成了漩涡。由于这两个漩涡的存在,在弯管处,流体的流通面积减小,流体向中间汇集,导致管道截面上中心处的流体速度增大,两侧贴壁处流速减小,引起流体旋转。
2.4 弯管后二次流的持续发展情况
2.4.1 二次流产生的原因
二次流,即叠加于主流并与之垂直的附加流动,是发生在垂直于流动平面内的一种流动。产生二次流的主要原因是流体受到了附加力的作用,如离心力、哥氏力、电磁力等。弯管内的二次流主要是指迪恩涡,它的产生使流体运动过程中阻力产生的能量损耗增大[5]。矩形弯管内的二次流如图7所示。弯管外侧的压强比内侧的压强高,即处的压强比处的压强高。弯管上下靠近壁面的两侧,即和处,因为流速比较低,离心惯性力比较小,所以压强也比较小,这样在弯管某一截面上沿壁面就形成了从外侧到内侧的压强降,即:>>、>>[6],结果在壁面上就形成了流体从外侧向内侧的流动。与此同时,由于连续性以及离心惯性力的作用,处的流体沿线从内侧向外侧流动。这样在弯管的某一截面上就形成了两个环流,即二次流[1]。二次流和主流叠加在一起,使得弯管内的流体质点作螺旋运动,这样就加大了弯管内流体的能量损失,即二次流损失[7]。
图7 矩形弯管内的二次流
2.4.2 二次流随曲度变化的规律
为了探索90°矩形弯管内压力场和速度场的分布和了解二次流损失随弯管曲度的变化情况,应用Fluent软件对不同曲度下的弯管内的二次流进行了数值模拟。在模拟过程中,在模型的基础上运用有限体积法对弯管空间进行离散,并使用带有旋流修正的k-ε模型进行计算。
为更直观地观察弯管后二次流的产生、过渡、消失的过程,在不同曲度下做出多个切片,展示切面上的速度矢量图如图8所示,值为距离弯管出口处的距离。以=4.05为例,在弯道入口前没有二次流的产生进入弯道后,=3.5为二次流最强处,=5为二次流消失处,中间部分为二次流过渡段。类似地,分别取曲度1.05、1.55、2.05、2.55、3.05、3.55、4.05、4.55,观察各曲度二次流最强处、二次流过渡段、二次流消失处的位置。为更清楚地了解二次流各阶段位置随弯管曲度变化的情况,运用Origin将各组数据汇总至曲线图中可知,随着弯管曲度的增加,二次流的影响范围越来越广。

图8 二次流各阶段位置随弯管曲度变化
2.5 求取流体对弯管的作用力
在实际管道计算中,经常会遇到求解运动流体和固体壁面之间的相互作用力的问题,如果已知运动流体作用在固体壁面上的压强分布情况,那么沿整个作用面对压强进行积分就可以求得运动流体对固体壁面的作用力。因此运用N-S方程来求取固体壁面上压强的分布,从而解得作用力的大小。即:
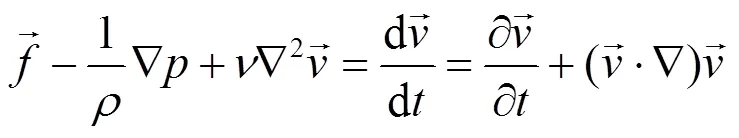
但N-S方程涉及到多阶导数的求解,运算过程较为复杂,因此运用动量方程来求解运动流体与固体壁面之间作用力的大小,即:

在此之前已求得出口和入口速度的大小和方向,代入表达式即可求得作用力的大小。
在Fluent中,可运用report功能将流体对弯管作用力的大小及方向读出。在读取出数据后,对力进行合成,求取出合力大小,并应用excel作出力随曲度变化的曲线图,如图9所示,可知,随着弯转曲度的增加,合力的大小不断增大。
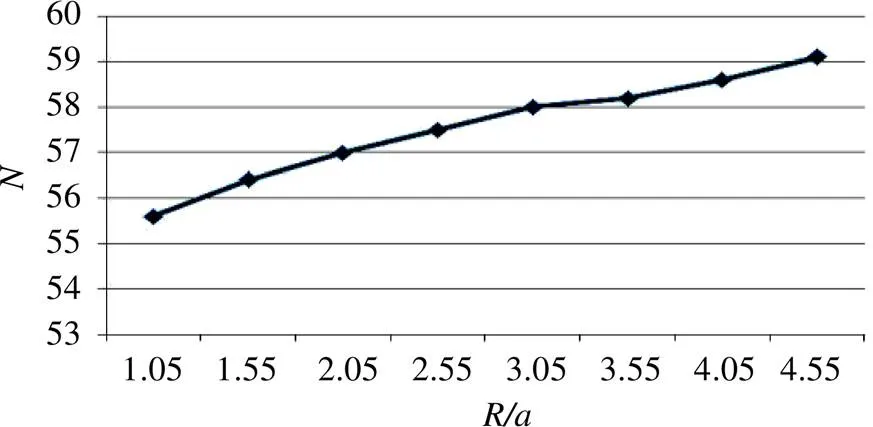
图9 合力随曲度的变化曲线图
3 对在管道内加装导流板的研究
本例中,空气以15 m/s的速度在矩形管中流动,接近于实际生活中商场内中央空调管道中冷气的流动。由前文的分析可知,在弯管中会有漩涡及二次流的产生,因此管道中的能量损失主要是局部损失。为了减少能量损失,应该设法减小局部损失,而减小局部损失的关键就在于减弱二次流的强度,缩小其在弯管后直管道内的影响范围。结合相关专业知识分析认为在弯道处加装导流板能够解决好该问题。
3.1 加装方式及性能分析
以=1.05为例。考虑到导流板的厚度会对管道内的空气流动产生阻碍作用,因此为了减少阻碍作用,其厚度也不宜过厚[8],最终取厚度为0.005 m。导流板的数量和安装位置也都有可能会对导流的效果产生一定影响。安装数目过多则会阻碍管道内空气的流动,安装数目过少则难以达到减少流动局部损失的目的,在本例中导流板数量在2片时的效果最佳。对于安装位置,在弯道的1/4和3/4处安装导流板是较为常见的做法,因此分别在这两处安装了导流板,然后检验其效果。
3.2 效果分析
未加导流板时的压力云图和速度云图如图10所示,发现此时管道内侧的压强在空气流经弯道处时急剧下降、速度急剧上升,在空气流过弯道进入直管道后内侧的压强急剧上升而速度急剧下降。空气流动除了主流流向外,还有发生在垂直于主流流动的一种流动,即二次流。它是由于管道内部的横向压力的作用,产生的平行于边界的偏移。内侧流体在二次流的带动下穿过横截面中心区域向外侧流动,从而使下游管道产生能量的耗散。这个二次流与主流叠加使通过弯道的流体质点作螺旋运动,加大了局部损失。
加装导流板后的压力云图和速度云图如图11所示,发现此时的压强分布和速度分布较未加装时更为均匀。如图12所示,弯管后最强处的二次流较未安装导流板时弱。读取管道进出口压强,代入伯努利方程,沿程损失和局部损失公式进行一系列计算,发现局部损失系数由未加装导流板前的0.6降至加装后的0.157,说明加装导流板后局部损失大大减小。
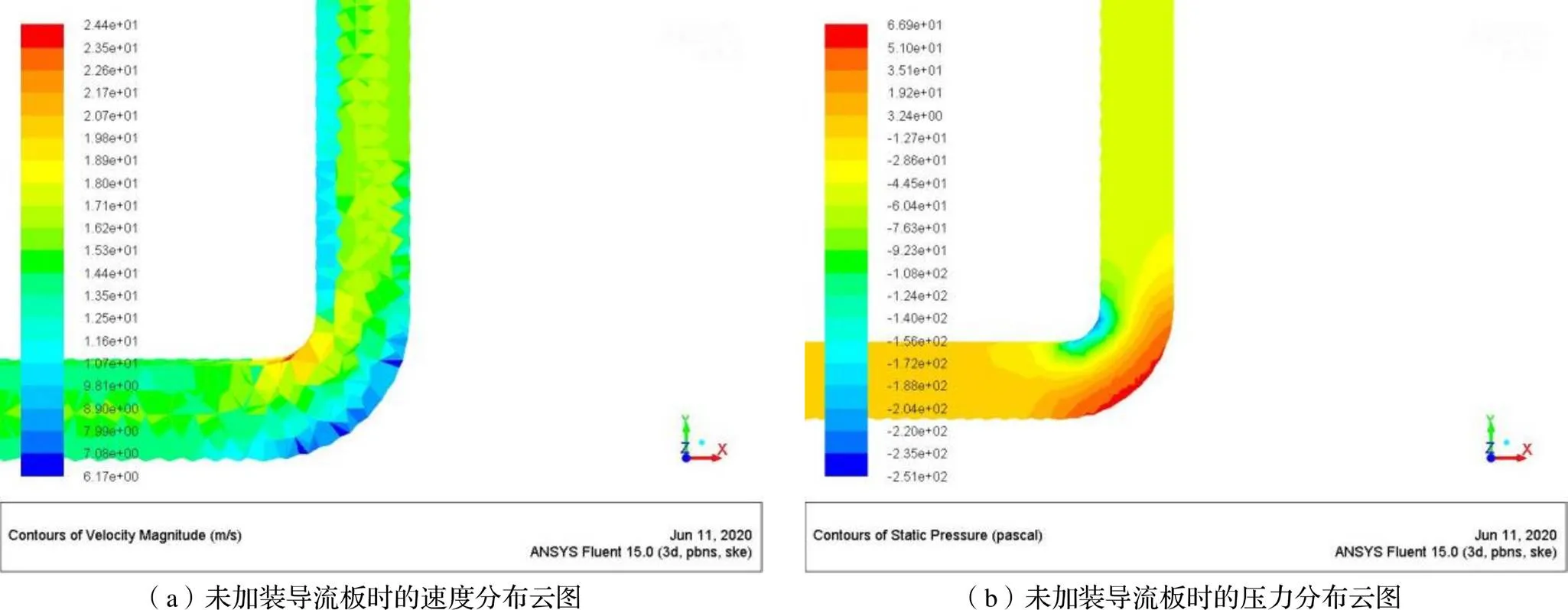
图10 未加装导流板时的速度分布和压强分布云图

图11 加装导流板后的速度分布和压力云图
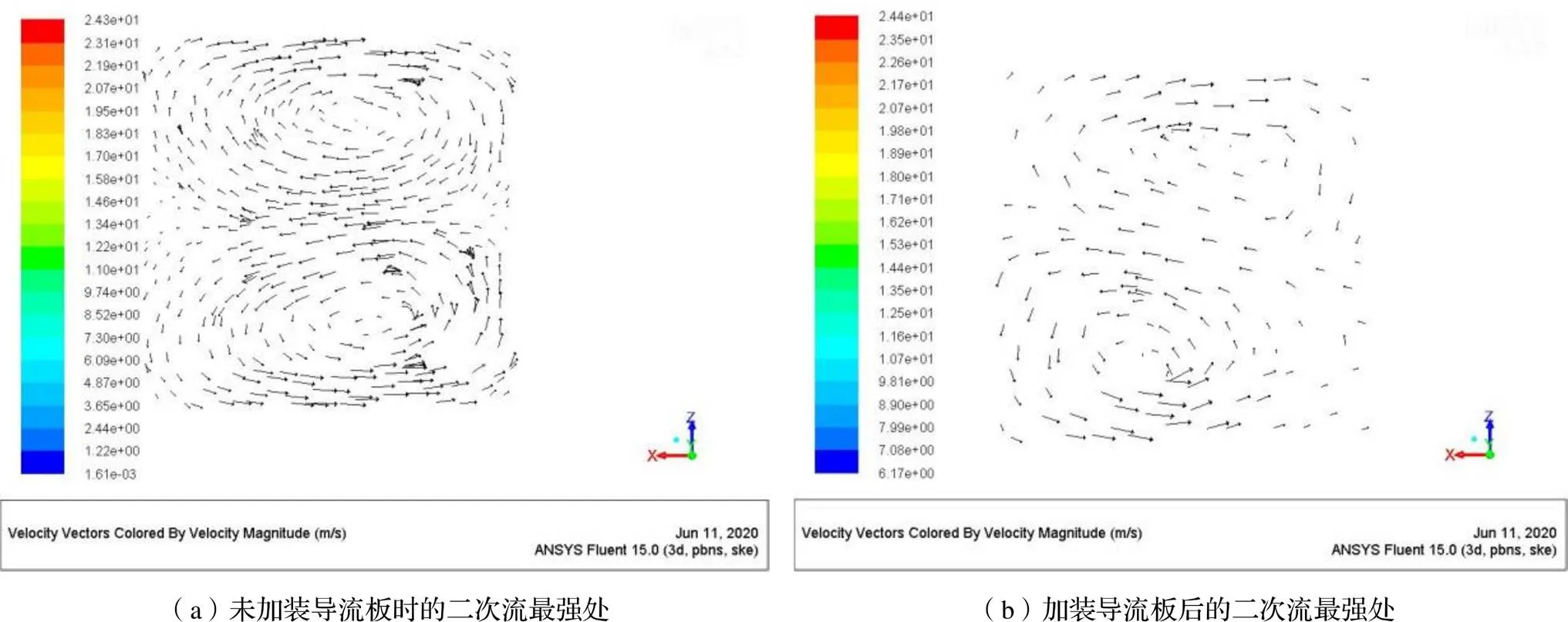
图12 两种情况下二次流最强处对比
4 结论
以Fluent进行数值模拟的方式分析矩形弯管曲度对管内空气流动情况的影响,得出以下结论:
(1)管内静压沿流体流动方向逐渐降低,直管部分压强分布较为均匀,弯管拐点处外侧压力很高而内侧压力很低(为负压),此处内外侧的压差导致二次流的产生。
(2)随着弯管曲度的增大,弯管进口截面压强和局部损失系数均减小,流体对弯管的作用力增大,基本随曲度呈线性变化,局部损失系数逐渐下降。
(3)管内流体流动速度沿流动方向略有降低但整体变化不大。直管部分速度分布比较均匀,弯管拐弯处速度外侧小内侧大,与压强分布大小相反。
(4)流体流经弯管后产生二次流,随着弯管曲度的增大,弯管后二次流最强处、过渡段及消失处离弯管出口的距离均增大,即二次流的影响范围扩大。
(5)流体流经弯管时,在弯管出口壁面处产生漩涡。
(6)增设导流板后,管内压强和速度分布更为均匀,二次流减弱,经计算得局部损失系数由加导流板之前的0.6降至0.157,局部损失大大减小。
[1]王松岭. 流体力学[M]. 北京:中国电力出版社,2007.
[2]王会凤. 应用广泛的金属挤压工艺[J]. 金属世界,2011(5):10-12.
[3]李跃. 恒壁温工况下螺旋管内流体流动及传热性能模拟研究[D]. 兰州:兰州交通大学,2016
[4]刘天昀,徐星宇. CPU液冷散热器的性能分析及结构优化[J]. 制冷,2020(3):44-50.
[5]张吉礼,马良栋,任晓东. 小曲率矩形截面弯管内流动特性数值模拟[J]. 建筑热能通风空调,2009(03):2-4.
[6]湛含辉,朱辉,陈津端,王刚. 90°弯管内二次流(迪恩涡)的数值模拟[J]. 锅炉技术,2010(4):1-5.
[7]丁钰,翁培奋. 90°弯管内流动的理论模型及流动特性的熟知研究[J]. 计算力学学报,2004,21(3):314-321.
[8]王周君,黎星华,唐立军,等. 矩形截面直角弯管内置导流板的优化研究[J]. 华电技术,2019,41(8):32-37.
Numerical Simulation of Internal Flow Field in 90° Rectangular Bend Pipe under Different Curvatures
LIU Tianyun,XU Xingyu,LI Chenbin,JIAO Huijie
( School of Energy, Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China )
In order to study the internal flow field of 90°rectangular bends under different curvatures, pipeline models are constructed with Gambit software, and the numerical simulation of the air flow in rectangular bends under different curvatures (=1.05~4.55) is conducted by using Fluent software and the Standard k-epsilon model air flow in rectangular bends under different curvatures (=1.05~4.55). The static pressure and velocity distribution in the pipe, the location and strength of the vortex, the local loss coefficient of the pipe under different curvatures and the stress condition of the bent part of the pipe are analyzed. And the development of the secondary flow after the bend and the effect of installing guide vanes to reduce the local loss coefficient are investigated as well. The results show that as the curvature of the bend increases, the pressure of the inlet section decreases, the local loss coefficient decreases, the fluid force on the bend increases, and the influence range of the secondary flow after the bend increases; after installing the guide vanes, the pressure distribution and the velocity distribution in the pipes become more uniform, the secondary flow is weaker, and the local loss coefficient is greatly reduced.
rectangular bend;curvature;numerical simulation;guide vanes;local loss coefficient
TK011
A
10.3969/j.issn.1006-0316.2021.01.002
1006-0316 (2021) 01-0006-08
2020-06-04
刘天昀(2000-),男,广东广州人,主要研究方向为热能与动力工程,E-mail:494272220@qq.com。
