加周期纵肋圆柱壳声辐射

童韫哲，范 军，王 斌，汤渭霖

（上海交通大学高新船舶与深海开发装备协同创新中心；海洋工程国家重点实验室，上海200240）

0 引 言

水下圆柱壳体的振动和声辐射问题一直是噪声控制领域研究的热点[1-2]，圆柱壳作为水下潜器的主要结构形式通常采用环肋和纵肋作为加强筋。环肋沿圆柱壳轴向周期分布，它所产生的反力主要改变轴向振动状态，引起轴向模态的耦合。而本文所研究的纵肋则是沿周向周期分布，它所产生的反力主要改变周向振动状态，引起周向模态的耦合。

目前对于加环肋、特别是周期性环肋圆柱壳的振动和声辐射的理论[3-5]和实验[6]都有了较深入的研究，对类似的加筋平板声辐射问题也有较详细的研究[7-9]，而对加周期性纵肋圆柱壳的声辐射问题尚缺乏深入的研究。谢官模等[10]导出了环肋、舱壁板和纵肋增强的无限长圆柱壳辐射声场的计算公式，分析了环肋、舱壁板和纵肋对辐射声压的影响。之后廖长江等[11-13]将它推广到有限长圆柱壳的情况，分析了纵肋对壳体表面平均振动速度的影响。但是，目前对于纵肋的作用仅仅是把它当成附加质量，忽略了周期纵肋间的相互作用对壳体振动和声辐射的影响。对加肋平板声辐射问题的一系列研究显示，当肋骨等间隔分布时，周期性结构中存在的Bloch弯曲波对板的振动和声辐射有显著影响[7]。

为了研究周期性纵肋对圆柱壳声辐射的影响，本文首先导出周期加纵肋无限长圆柱壳的振动和声辐射公式。壳体振动用薄壳理论的Donnell方程描述，考虑纵肋的纵振动和弯曲振动。通过周向模态展开和轴向Fourier 变换导出圆柱壳体径向振速表达式，使用稳相法积分得到远场辐射声压的解析解。在此基础上，计算了接收点正对激励点时，加不同数量纵肋的远场辐射声压级，对比了考虑和忽略周期纵肋间相互作用的情况，并据此进行了周期性纵肋对辐射声场影响的机理分析。研究表明：周期纵肋增加的附加质量能够使圆柱壳体中固有的弯曲波共振峰发生微小偏移，而周期性纵肋间的相互作用则能产生一系列附加的共振峰，它们由周期性结构的Bloch弯曲波中低于水中声波数的分量通过相位匹配方式高效辐射到远场。也就是说，周期性加肋结构增加了能有效辐射声波的低波数分量。

1 振动与声辐射控制方程

设圆柱薄壳的中面半径为a，壳体厚度为hs，杨氏模量为Es，泊松比为σs,密度为ρs，且hs/a≪1，纵肋横截面的高和宽用H和W表示。取原点为O的正交坐标系，R是观察点到原点的距离，如图1所示。壳体振动用中面在z、φ和r方向的位移u、v和w来表示。壳体浸没在密度为ρf，声速为cf的流体介质中。

图1 无限长纵向加肋圆柱壳示意图Fig.1 Geometry of infinitely long cylindrical shells with periodic lengthwise ribs

无限长圆柱的振动在纵向形成行波，设解为

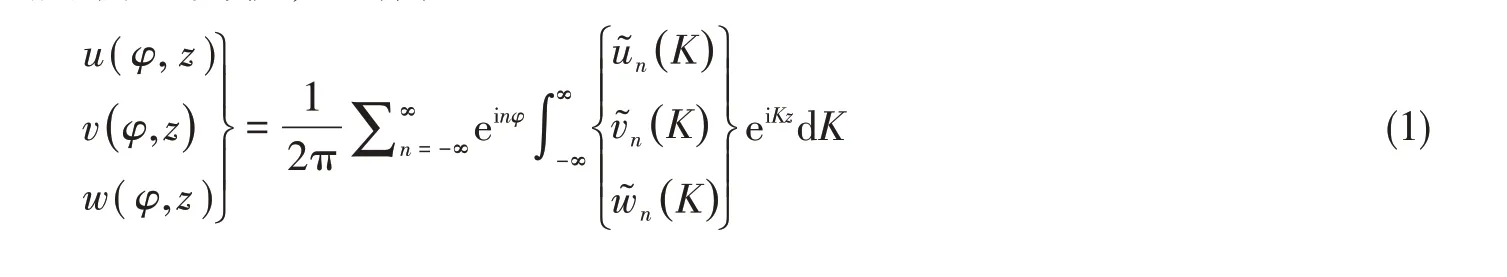
同时将激励力也分解为

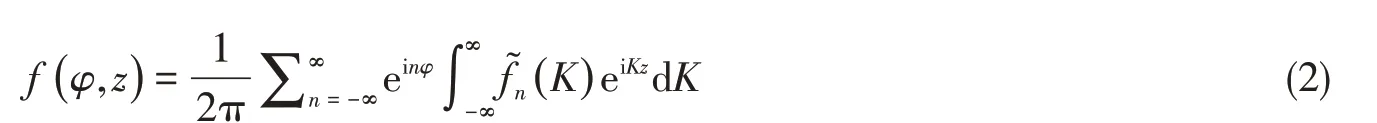
利用正交关系式得到展开系数

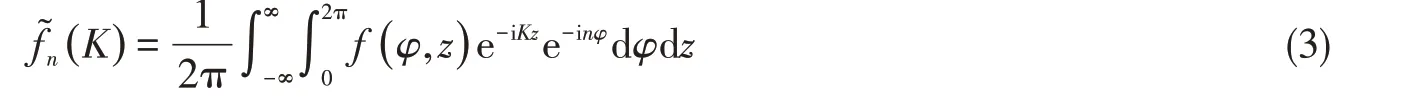
将纵肋简化为横截面积为A=H×W的等截面直细梁，设纵肋的材料与圆柱壳的相同。纵肋的振动包括纵振动、弯曲振动和扭转振动。由于扭转振动的等效力是扭矩的导数，当肋很细时扭转的作用相当于四极子源，辐射效率比较低，可以忽略。壳体振动采用Donnell 方程，省略时间因子e-iωt，得到n阶振动满足的控制方程[14]为

n'=n时为n阶自阻抗，否则为互阻抗。φl是第l根纵肋的圆周角，在均匀分布的情况下，纵肋间隔Δφ= 2π/T。为简单起见，当纵肋均匀分布时设φ0= 0，利用等比级数求和的公式得到

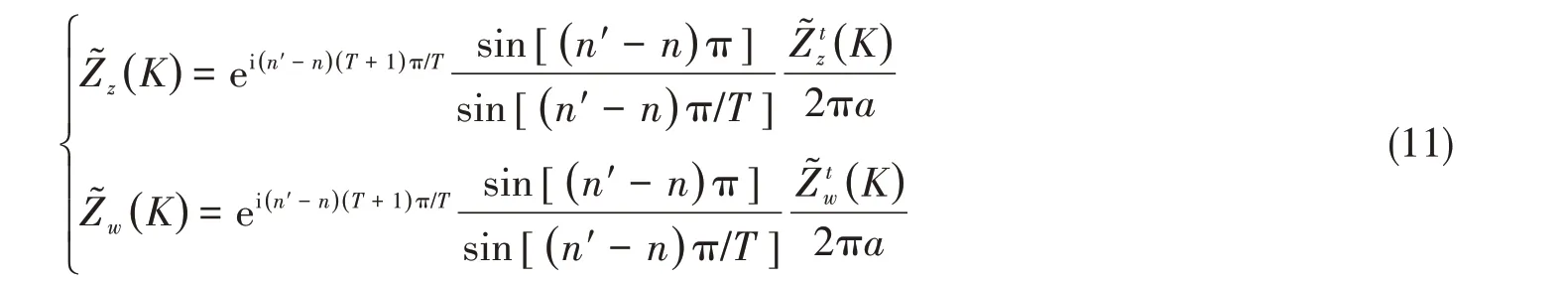
即

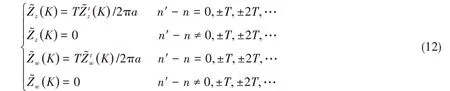
2 数值计算和结果分析

基于以上理论分析，通过数值算例分析周期性纵向加肋对水中圆柱壳振动和声辐射的影响。取圆柱壳体的基本参数：a= 1 m，壳体厚度hs= 0.01 m，壳体上均匀排列了T根纵肋；密度ρs=7 850 kg/m3，Es=210 GPa，泊松比σs= 0.3；纵肋横截面宽W= 0.03 m，纵肋横截面高H= 0.05 m；水的密度为ρf= 1 000 kg/m3，声速为cf= 1 500 m/s。本文用来描述壳体声辐射的量为在单位集中力（1 N）作用下，参考声压为1 μPa，接收点正对激励点，从远场辐射声压折算到距声中心1 m处的声压级。

首先计算了加8 根纵肋圆柱壳与基本圆柱壳的远场辐射声压，并对比了考虑互阻抗和忽略互阻抗的情况，如图2所示。横坐标为频率，取值范围是0.1-2 000 Hz，计算点间隔随频率指数增长。

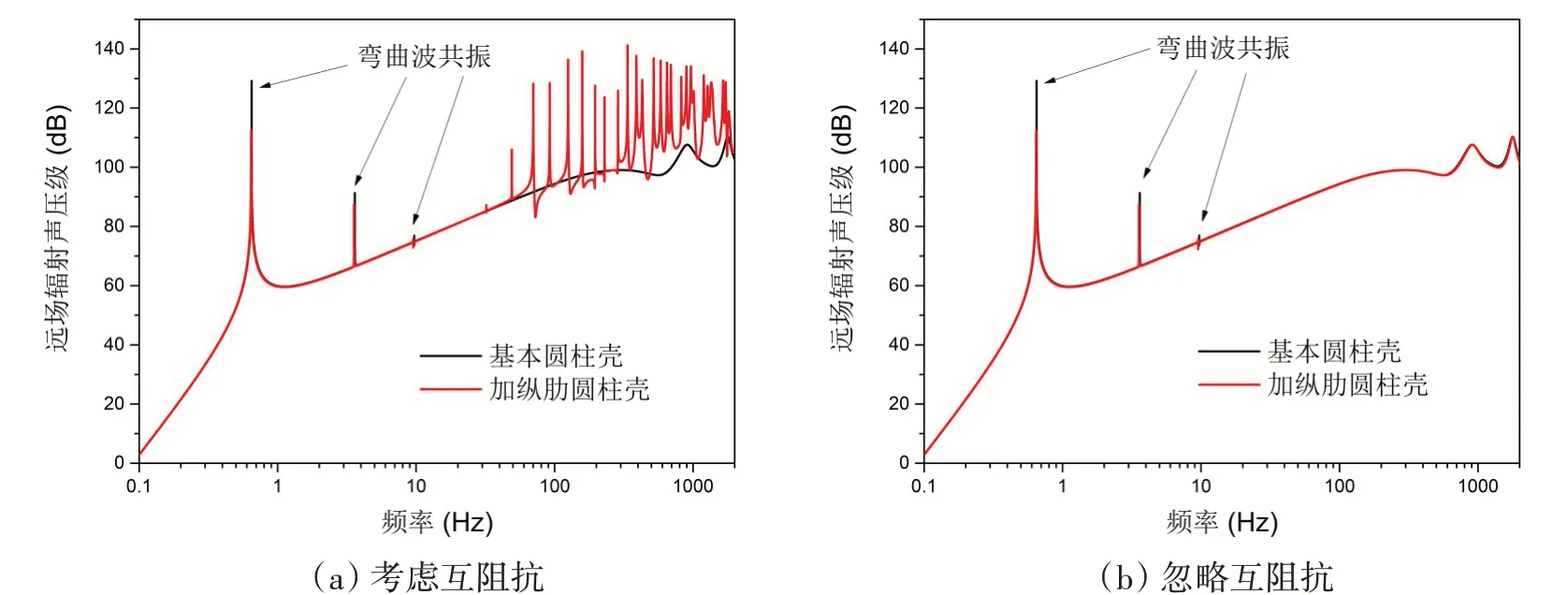
图2 加8根纵肋圆柱壳远声辐射声压级Fig.2 Sound pressure level of a cylindrical shell with 8 ribs

对比图2（a）和图2（b）可以看出，在低频段（小于10 Hz），基本圆柱壳和加纵肋圆柱壳均可观察到3 个共振峰，这是由弯曲波在周向形成共振产生的[17]。不同的是加纵肋后，这三个弯曲波共振峰的位置有所偏移。在中高频段（大于10 Hz），忽略互阻抗时，加纵肋圆柱壳的辐射声压级与基本圆柱壳基本一致；考虑互阻抗时，加周期性纵肋圆柱壳的辐射声压级新增了一系列共振峰。

2.1 周期性纵肋对弯曲波辐射的作用

本文主要计算的是接收点正对激励点的远场辐射声压级，此时沿圆柱壳周向传播的弯曲波对辐射声场起主要作用。为了研究纵肋对弯曲波辐射的作用，首先计算了水中基本圆柱壳中沿周向传播的弯曲波频散曲线。对于只考虑周向传播的弹性波时，轴向波数K= 0，振动方程可以写成

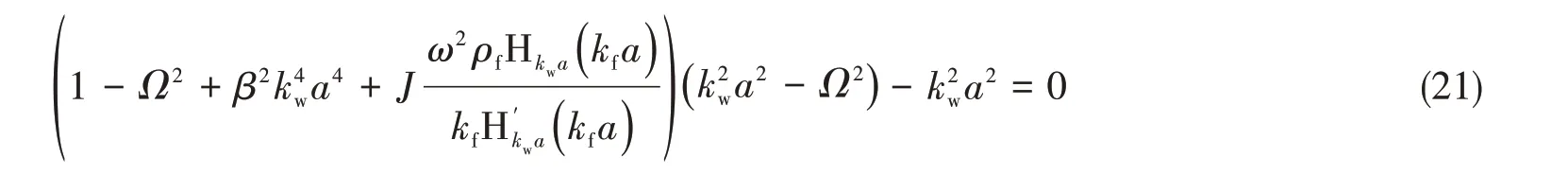
基于公式（21），图3 给出了弯曲波的频散曲线，分别画出了弯曲波波数实部和虚部随频率变化曲线，并在此基础上解释了弯曲波的辐射机理。

由图3（a）可知，在本文计算频段（0.1-2 000 Hz），弯曲波波数远大于水中声波数，弯曲波是亚音速波，其表面振动能量无法通过相位匹配的方式高效辐射到远场。但由于圆柱壳表面存在曲率，弯曲波波数在频率较低时虚部较大，如图3（b）所示。此时，亚音速的弯曲波也能辐射很小一部分能量到远场[16]。

由于亚音速弯曲波波数的实部远大于水中声波数，其虚部也非常小，所以这些共振峰的带宽非常窄。随着频率的增加，圆柱壳体的声学特征逐渐趋近于平板，弯曲波波数的虚部逐渐趋近于零，弯曲波共振峰的带宽也逐渐减小，只有计算间隔足够小才能捕捉到共振峰。图2 中只计算到前三个弯曲波共振峰，实际上频率较高时也存在弯曲波共振峰，只是频率较高时弯曲波共振峰宽度更窄，计算步长也更大，跳过了这些共振频点。值得注意的是，此类共振峰在无限大平板的远场辐射声压中并不存在。

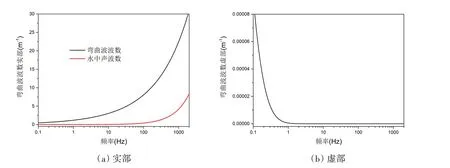
图3 基本圆柱壳弯曲波波数Fig.3 Wave number of flexural wave in unribbed cylindrical shell

为了研究纵肋在低频时的作用，以第一阶弯曲波共振峰为研究对象，计算了加不同数量纵肋时第一阶弯曲波共振峰附近的辐射声压级，对比了考虑互阻抗和忽略互阻抗的情况，如图4所示。

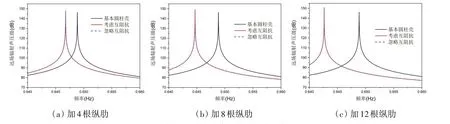
图4 加不同数量纵肋圆柱壳远场低频声辐射声压级Fig.4 Sound pressure level of a cylindrical shell with different numbers of ribs in low frequencies

观察图4可知，周期性加肋对弯曲波共振峰有影响。随着纵肋数量的增加，弯曲波共振峰逐渐向低频移动。但是，纵肋互阻抗对弯曲波共振峰没有明显影响，说明起作用的主要是纵肋自阻抗。自阻抗引起的附加质量导致整体结构质量增加，使弯曲波共振峰向低频移动。

2.2 周期性纵肋的Bloch弯曲波对声辐射的作用

为了进一步研究周期性纵肋对辐射声场的影响，本节详细讨论了由周期性纵肋引起的辐射声场中、高频段的附加共振峰。图5是加不同数量纵肋圆柱壳与基本圆柱壳的辐射声场的对比图，分别计算了考虑互阻抗和忽略互阻抗的情况。纵坐标是辐射声压级，横坐标为频率，取值范围是0.1-2 000 Hz，计算点间隔随频率指数增长。

图5（a）对比了忽略互阻抗时，加不同数量纵肋与基本圆柱壳辐射声场的对比图，可以看出除了低频处三个弯曲波共振峰的位置稍有不同，中、高频段加不同数量纵肋圆柱壳与基本圆柱壳的辐射声压级基本相同。图5（b）-（c）分别是加4根、8根和12根纵肋圆柱壳辐射的声压级，对比考虑互阻抗和忽略互阻抗的情况。可以看出，当考虑互阻抗时，辐射声压级的中、高频段出现了一系列附加共振峰。

纵肋的互阻抗体现了纵肋间的相互作用，当考虑纵肋间的相互作用时，周期性纵肋使得圆柱壳变成沿周向的无限周期结构。对于无限大平板，如果其弯曲波波数为kw，那么周期加肋平板中的第m阶Bloch弯曲波可以写成

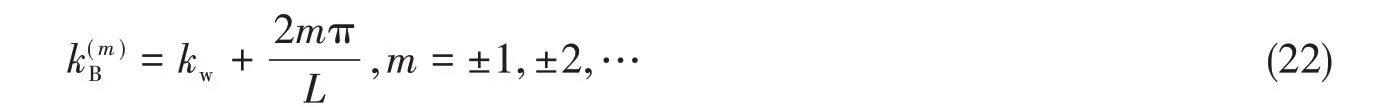
推广到加周期纵肋圆柱壳，将其周向弯曲波波数同样记作kw，纵肋的间隔L= 2πa/T。那么沿圆柱壳周向的第m阶Bloch弯曲波可以写成

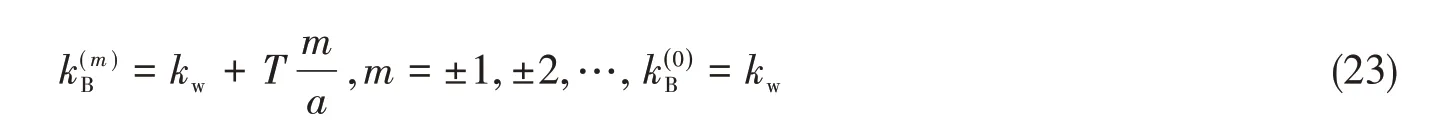
其中m= 0是基本传播模式，即圆柱壳周向弯曲波。其余是由于周期纵肋的相互作用引起的附加传播模式，可称为Bloch弯曲波传播模式。

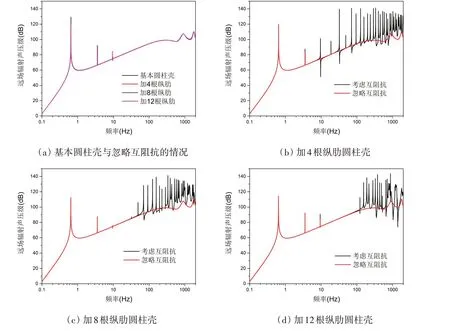
图5 周期性纵肋对圆柱壳远场辐射声压级的影响Fig.5 Influence of periodic ribs on sound pressure level

3 结 论

为了研究周期性纵肋对圆柱壳辐射声场的影响，本文通过周向模态展开和轴向Fourier 变换导出点激励情况下加周期纵肋无限长圆柱壳表面振动计算公式，通过稳相法得到了远场辐射声压的解析解表达式。数值计算给出了接收点正对激励点时远场辐射声压级的频率谱，并解释了纵肋自阻抗和互阻抗对辐射声场的影响，研究表明在无限长加周期纵肋圆柱壳中存在两类声辐射机理：

（1）低频段的弯曲波辐射机理。在圆柱壳中，弯曲波绕行壳体一周相位变化2π的整数倍，壳体在周向形成驻波共振。在本文计算频段，亚音速的弯曲波波数小于水中波数，这部分振动能量无法通过相位匹配的方式高效辐射到远场。由于圆柱壳体表面存在曲率，仍有极小部分的能量辐射到远场，并且形成带宽非常窄的共振峰。因此，弯曲波共振峰在低频处带宽较宽，随着频率增加，圆柱壳的声学特征逐渐趋近于平板，弯曲波共振峰带宽逐渐减小，只有计算频率间隔足够小时才能得到。

（2）中高频段的Bloch 弯曲波辐射机理。加周期纵肋后，由于纵肋间的相互作用，在圆柱壳周向存在多阶次的Bloch 弯曲波传播模式，Bloch 弯曲波绕行壳体一周相位变化2π 的整数倍，也能在壳体周向形成驻波共振。不同于亚音速的弯曲波，Bloch 弯曲波波数小于水中声波数的分量，能够通过相位匹配的机理高效辐射到远场，并形成一系列的附加共振峰。Bloch 弯曲波辐射频段存在下限，其频率下限与纵肋的间距有关，纵肋间距越大辐射频段的下限越低。