角分辨布里渊光散射对材料的弹性和热学性能研究的综述
2021-03-08庞思敏谢亚茹张俊
庞思敏,谢亚茹,张俊,*
(1.中国科学院半导体研究所,半导体超晶格国家重点实验室,北京 100083;2.中国科学院大学,材料与光电研究中心,北京 100049)
1 引言
材料的弹性和热学性能对于研究其基本性质以及很多有趣的物理现象具有重要的意义,如钙钛矿中自陷激子(self-trapped excitons, STEs)的形成[1]、声子瓶颈效应[2]等。研究材料的弹性和热学性能有助于人们对这些性质进行外部调控并根据材料的性质将其应用到不同的器件中,如高弹性模量的材料可用于设计通信和传感装置的高频谐振腔[3,4];低弹性模量的材料如具有生物相容性的钛合金可用于各种生物工程[5];高热导率的材料可用作设备的“散热器”,将热点处的热量快速地向各个方向传导出去,解决设备的热耗散问题[6];低热导率材料可用于热电设备[7]等。因此,弹性和热学性能对于器件的设计和制备,设备的稳定运行以及性能优化等起着指导作用。另外,由于量子限制效应,二维材料的弹性和热学性能与块体的不同,研究尺寸效应以及微结构等如何影响材料的弹性和热学性质,对基于二维材料的小型化器件的进一步发展具有重要的参考价值。
器件的力学和热学稳定性与材料的弹性性质密切相关。目前研究材料弹性性质的主要方法包括机械应力-应变法[8],共振超声光谱(resonance ultrasonic spectroscopy, RUS)[9]和非弹性中子散射(inelastic neutron scattering, INS)光谱[10]等,然而这些方法均要求大的样品体积,不适用于研究低维材料。对于布里渊光散射(Brillouin light scattering, BLS)光谱[11],其是一种非接触的无损光学探测方法,可以获得弹性常数的特定分量以及特定晶向的晶格热导率而非其空间平均值。微区BLS光谱的空间分辨率可达到亚微米量级,可用于探测二维材料的基本元激发。角分辨BLS光谱测量通过改变探测到的声学声子的波矢,可得到其色散关系并利用声速求解材料的弹性常数和晶格热导率等物理量。相比于其它技术,利用角分辨BLS光谱可以更加简便地获得材料的各个弹性常数,结合沿任意方向传播的声学声子的声速计算公式可更快速地求解材料中沿任意方向的声速及相应方向的晶格热导率。同时,可利用角分辨BLS光谱研究外部工程如何调控材料的弹性和热学性质以及研究声子瓶颈效应等与声子散射相关的物理现象。
本文综述了利用角分辨BLS光谱研究材料的弹性和热学性能的基本原理、实验方法和相关实验进展。首先介绍BLS的基本原理以及如何获得角分辨BLS光谱,然后分别介绍如何利用角分辨BLS光谱获得材料的弹性常数、德拜温度和晶格热导率等物理量,最后介绍角分辨BLS光谱技术在确定块体、薄膜以及二维范德瓦尔斯材料的弹性性质和热导率等方面的一些实验结果。
2 基本原理
2.1 布里渊光散射的原理
布里渊光散射是一种由产生随时间变化的密度调制的凝聚态物质系统,如声学声子(声波)或磁振子(自旋波)等的集体激发而产生的非弹性光散射[12]。本文讨论的准粒子均为声学声子,磁振子暂且不讨论。BLS的经典图像:以声速υ传播的声学波导致介质中密度发生周期性变化,从而导致局部介电常数的周期性变化,同时折射率也被周期性调制,因此声学波相当于一个移动的衍射光栅,入射光可以在这里被反射。由于多普勒效应,散射光的频率相对于入射光会发生改变。如果密度调制(声学波的波矢q)向入射光靠近,则散射光频率增加,对应反斯托克斯(anti-Stokes)过程(图1(a))。反之,如果密度调制远离入射光,对应斯托克斯(Stokes)过程(图1(b))。BLS的量子力学图像:BLS来源于光子与传播的布里渊区中心附近的声学声子的相互作用。在散射过程中,遵循能量和动量守恒,
hks=hki±hq,
(1)
hfs=hfi±hf,
(2)
其中ki和ks分别对应样品内部入射和散射光的波矢,q为声学声子的波矢,f为布里渊频移,fi和fs分别为入射和散射光的频率。“±”分别对应声子的产生和湮灭,即反斯托克斯(图1(c))和斯托克斯(图1(d))过程。
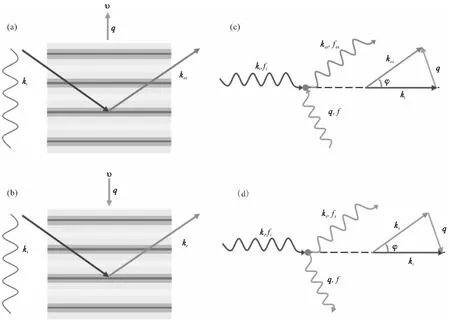
图1 布里渊光散射(BLS)的经典图像和量子力学图像示意图。(a)反斯托克斯(anti-Stokes)和(b)斯托克斯(Stokes)过程的经典图像示意图;(c)反斯托克斯(anti-Stokes)和(d)斯托克斯(Stokes)过程的量子力学图像示意图。ki和ks/kas分别为样品内部入射和斯托克斯/反斯托克斯散射光的波矢,q(υ)为声学声子的波矢(速度),f为布里渊频移,fi和fs/fas分别为入射和斯托克斯/反斯托克斯散射光的频率,φ为入射光和散射光之间的夹角
通过改变样品的厚度、入射角以及入射和散射光的偏振条件等,BLS光谱可以探测到的声学声子主要分为两大类[13]:在材料体内传播的体声学波(bulk acoustic wave, BAW):包括纵向声学(longitudinal acoustic, LA)波和横向声学(transverse acoustic, TA)波;在表面传播的表面声学波(surface acoustic wave, SAW):包括在自由表面附近传播的瑞利表面声学波(Rayleigh surface acoustic wave, RSW)、伪瑞利表面波(当RSW的声速足够大时,其能量将不能被限制在表面附近,而是逐渐向体内泄漏,形成泄表面声学波,也叫伪瑞利表面波)、在表面传播的剪切水平波(shear horizontal wave, SHW),以及在近表面区域传播的掠面体波(surface skimming bulk wave, SSBW,当沿表面传播的高能SHW向体内指数衰减传播时,会形成泄体声学波。SSBW是泄体声学波的一种)等。当材料的厚度处在与声学长度可比拟的亚微米量级时,在BLS光谱中会观察到一系列不同声速和阶次的Sezawa模式,该模式的色散随着材料的厚度变化,一般在较厚的样品和较大入射角的条件下,会出现更多阶次的Sezawa模式[14]。
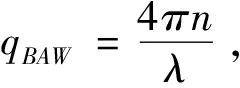
(3)
而根据面内动量守恒,SAW的波矢大小为

(4)
其中θi为入射角。长波极限下,声学声子的色散关系是线性的,声速υ对应色散关系的斜率,即

(5)
对于BAW和SAW,其声速表达式分别为
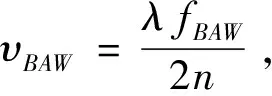
(6)

(7)
对于背散射配置下的BLS光谱测量,当改变入射角θi时,SAW的波矢大小发生改变,可以通过转角得到其色散关系。另外,随着θi的变化,虽然BAW的波矢大小不变,但方向发生了变化,即可以测量到沿不同方向传播的BAW。理论上,可以通过保持样品不动转动入射光或者入射光路固定,转动样品的方法来改变入射角,但对于背散射配置下的BLS光谱测量,通常会选择在样品上安装旋角仪,通过转动样品,改变入射光与样品表面法线的夹角θi(图2(a)),其测量结果对应角分辨布里渊光散射(BLS)光谱。对于角分辨BLS光谱,需要考虑波矢不确定度(图2(b))的问题,SAW波矢大小的分布可表示为[15]

图2 角分辨BLS光谱的装置及波矢不确定度示意图。(a)角分辨BLS光谱的装置示意图,为样品外部(内部)入射光/散射光的波矢,qBAW/qSAW为体声学波/表面声学波的波矢,θi为入射角,θ'i为样品内部的折射角;(b)角分辨BLS光谱测量中波矢不确定度的示意图,φ为实验中使用的物镜的收集角
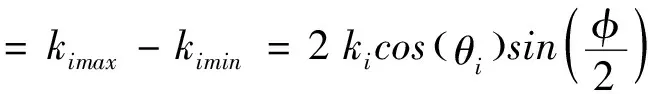

(8)

2.2 角分辨BLS光谱与晶体的弹性性能
由于材料的声速υ与弹性常数相联系[16],
(9)
其中X为弹性常数Cij的组合,ρ为材料的密度,因此可以利用从BLS光谱中获得的声速求解材料的弹性常数。具体求解过程[17-18]如下:
长波近似下,对于传播的BAW,其运动方程可写成
(10)
其中u为偏离平衡位置的局域位移矢量,Ciklm为弹性刚度张量的矩阵元素。将平面波解代入上式,可以得到
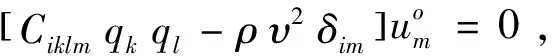
(11)
其中q为特定声学声子的单位波矢的方向余弦。当久期方程系数行列式为零时,
(12)
其中λij为qi与Cij的组合,

(13)
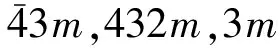
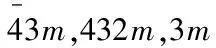
表1 立方晶系点群晶体中选定q的高对称方向上声学模的偏振矢量、种类、速度以及布里渊散射张量[17]
(14)
只有当入射和散射光的偏振方向满足偏振选择定则时,即I≠0时,相应的声学模式才能在BLS光谱中被探测到。
理论上,通过测量足够多方向的声速,可以得到给定晶体的全部弹性常数。特别地,通过选择特定的测量方向,如高对称方向,计算可以变得更简单。利用BAW的角分辨BLS光谱确定晶体的弹性常数这一方法的优势在于,角分辨BLS光谱结合沿任意方向传播的声学声子的声速计算公式后,可以在仅需测量少量单晶样品的情况下获得更多方向的声速,减少了大量特定晶向样品制备的复杂操作,从而大大简化了求解晶体全部弹性常数的过程,具体分析见3.1节。同时,如果材料的弹性常数已知,则对于任意给定的qi,即声学声子的传播方向已知,可直接通过上述公式求得三个不同的声速。
2.3 角分辨BLS光谱与晶体的热学性能
利用布里渊频移求得的声速可以用于沿任意方向晶格热导率的求解。根据slack方程[19],晶格热导率可表示为
(15)
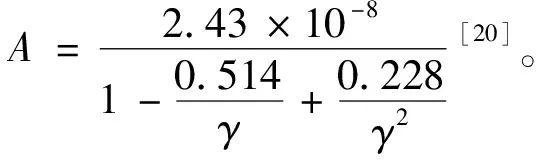
对于声学德拜温度Θa,可利用从BLS光谱中获得的声速并结合公式(16)和(17)[21]进行求解,
(16)

(17)
其中υL为纵向声速,υS为横向声速,υa为声子的平均速度,h为普朗克常数,kB为玻尔兹曼常数,m为单位体积中的原子数。
对于γ的计算,Jia等人[21]首先利用第一性原理计算得到材料的弹性常数,而后计算了弹性常数(声速)随体积V的变化关系,得到材料的平均声学格林艾森常数γ,
(18)
(19)
(20)
对于立方各向同性岩盐和闪锌矿结构,以及非立方各向异性纤锌矿结构而言,这一方法的计算结果与实验结果吻合得较好。然而,此计算方法需要专业的算法或软件辅助,对于想要简单直观地通过BLS光谱测量获得的声速来计算γ,不大可行。Belomestnykh[22]提出一种适用于岩盐结构晶体的热导率计算方法,可以简单地通过声速求得γ,
(21)
(22)
其中ν为泊松比。
κL对样品中的杂质非常敏感,特别是那些充当替位原子的杂质[19]。对于无序晶体,利用Cahill的模型[23]可以预测材料晶格热导率的最小值。Cahill模型是爱因斯坦模型的延伸,其假设振子的振动不会相互影响,同时认为振子的寿命是振动周期的一半。利用从BLS光谱中获得的纵向(υL)和横向(υS)声速可以计算晶格热导率的最小值。当温度高于德拜温度时,晶格热导率的最小值[24]可表示为
(23)
其中n为固体中原子的数密度。
3 分析与讨论
对于给定的材料,如果原子间的键合较弱,则其弹性常数也会很小,即在机械应力下,晶体结构可以很容易地发生形变。弱的原子间键合会导致强的晶格非谐性,进而使得材料的热导率很小。接下来主要总结利用角分辨BLS光谱技术确定块体、薄膜以及二维范德瓦尔斯材料的弹性性质和晶格热导率的一些实验结果。表2汇总了相关材料利用BLS光谱获得的弹性常数和热导率。

表2 利用BLS光谱获得的不同材料的弹性常数和晶格热导率
3.1 块体材料
金刚石的弹性模量很大,其优异的弹性和热学性能使得基于金刚石声学波的压电薄膜/金刚石多层结构已被应用于高频和大功率声学器件的研制中[29]。Xie[25]等人利用角分辨BLS光谱技术,指认了面心立方(fcc)结构板状(100)金刚石中的体声学声子以及表面声学声子。利用实验获得的体声学声子的声速,结合2.2和2.3节中的计算方法,得到了(100)金刚石中的超高弹性常数(C11=1069 GPa,C44= 565 GPa,C12= 101 GPa),德拜温度(1814 K)以及沿[100]晶向的晶格热导率(4106 W m-1K-1)。同时,给出了沿任意方向传播的体声学声子的声速计算公式。图3(a)和(b)分别对应fcc晶体第一布里渊区的1/8及其在kx-ky平面上的投影。光正入射到(100)金刚石的表面时,纵向声学声子的波矢沿着ΓΧ方向,随着入射角θi的增大,声子波矢方向逐渐从ΓΧ转向另一个高对称方向ΓK,通过对不同高对称方向声学声子的声速进行矢量叠加的方法可以对声速随θi的变化(图3(c))做出定量的解释,具体求解过程可参考文献[25]。理论上,此声速计算方法可以推广到其它晶体结构的材料。对于对称性较高的晶体结构,如立方晶系和六方晶系等,利用该方法求解沿任意方向传播的声学声子的声速较为简便,但随着对称性的降低,晶体的第一布里渊区变得复杂,增加了高对称方向声速叠加的困难。然而,相比于直接测量大量具有任意晶向的单晶样品的BLS光谱而后计算其声速,利用该声速计算公式可以在得到一定数目的沿不同高对称方向传播的声学声子的声速后,仅需对更少的单晶样品进行角分辨BLS光谱测量,即可获得该材料中沿任意方向传播的体声学声子的声速,总的来说,是一种更加简便的方法。当沿任意方向传播的声学声子的横向和纵向声速确定后,相应方向的晶格热导率也可以通过公式(15)进行求解。
相比于超高弹性模量的金刚石,钙钛矿的晶格相对较软,弹性常数较小[10]。Ferreira[26]等人利用非弹性中子散射光谱和角分辨BLS光谱得到四种不同的立方相单晶有机-无机杂化含铅卤素钙钛矿的声速,确定了材料的全部弹性常数以及体模量和各向异性系数等参数。这些钙钛矿的弹性常数较小,剪切模量C44非常低,抗剪切应力的能力差,热导率很低。近年来,基于杂化含铅卤素钙钛矿的热载流子太阳能电池引起了人们的广泛关注[30]。低的弹性常数(软的晶格)以及强的非谐性有利于增强钙钛矿中的热载流子效应。热载流子-声子弛豫速率τ与纵向声速的平方平均即平均弹性常数如C11成正相关,而前人发现的室温下α-FAPbI3中的τ比MAPbBr3体系中的小3-4倍的结果[31]与此实验获得的弹性常数结果[26]相吻合(图3(d)),因而证实了前人提出的用于解释热载流子弛豫的声子瓶颈假说。热声子瓶颈效应使得载流子很难通过发射声子的形式进行弛豫,可以提高热载流子太阳能电池的对外输出电压和能量转换效率,对于实现热载波光伏器件和突破单节太阳能电池中Shockley-Queisser效率极限是至关重要的[32]。角分辨BLS光谱技术为研究杂化钙钛矿中的声子瓶颈效应提供了一种新的思路。
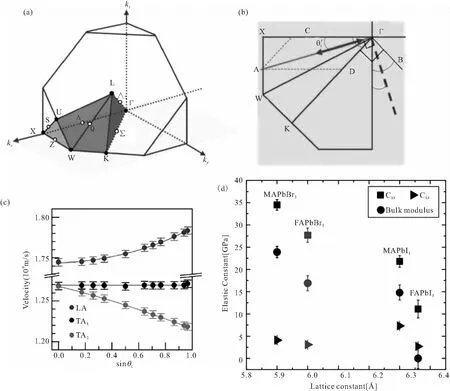
图3 角分辨BLS光谱研究块体材料的弹性和热学性能的相关示意图及实验结果。(a)面心立方晶体第一布里渊区的1/8[25]以及(b)其在kx-ky平面上的投影示意图,其中的罗马字母对应对称点和对称轴,对应实空间的折射角[25];(c)(100)金刚石中三支体声学声子的声速随sinθi的变化,其中θi为入射角,实心圆对应实验数据[25];(d)四种不同杂化钙钛矿的弹性常数C11、C44以及体模量K[26]
3.2 薄膜材料
对于各向同性的多晶薄膜材料,利用弹性动力学格林函数[33],可以通过角分辨BLS光谱测试获得的表面声学声子的色散关系确定材料的弹性常数。不同于上述块体材料中弹性常数的求解,此处使用到的是表面声学声子而非体声学声子的声速,计算方法也相对复杂,具体的计算过程可参考文献[33]。
Kuria[27]等人通过测量到的TaN薄膜的角分辨BLS光谱得到瑞利表面声学波(RSAW)以及Sezawa波(Sezawa wave, SW)的色散关系,并进一步确定了弹性常数C11和C44。使用类似的方法,Baloi[24]等人确定了非晶Ge2Sb2Te5和GeTe 薄膜的弹性常数。图4(a)为不同入射角下Ge2Sb2Te5薄膜的BLS光谱,可以发现在高入射角时,会出现更多阶的Sezawa波。图4(b)展示了Ge2Sb2Te5薄膜中沿[100]方向传播的声学声子的声速与平行于薄膜表面的声学声子波矢大小和薄膜厚度乘积k‖d的关系,结合弹性动力学格林函数可以求解弹性常数。利用从光谱获得的纵向和横向声速以及公式(23)可以确定晶格热导率的下界,两者的晶格热导率都很低(κLmin< 0.50 Wm-1K-1)。薄膜中结构缺陷和空位的出现会影响声子的散射,导致声子的平均自由程降低,进而导致材料中的低热导率。
3.3 二维范德瓦尔斯材料
Babacic[28]等人测量了块体以及不同厚度的少层二维范德瓦尔斯2H-MoSe2单晶的角分辨BLS光谱,得到了C11,C66以及C44的值。长波极限下,体声学声子的色散是线性的,且不直接依赖于材料的厚度,而声学兰姆波的角分辨色散与C11、残余应力σ0以及材料厚度d这三个参数有关。随着样品层数的减小,层间范德瓦尔斯相互作用力减小,作用在原子上的有效约束力(对应弹性常数)发生软化,出现了弹性尺寸效应(图4(c)和(d))。同样,材料的热导率也会存在尺寸效应。宏观尺度下,对于给定的材料,某一晶向的热导率一般只随温度变化,而随着层数的减少,材料的尺寸与声子平均自由程可比拟时,声子将倾向于在界面处发生散射而不是与其它声子发生碰撞,从而使得热传输速率降低[34]。通过改变材料的厚度,可以对其弹性性质进行调控并进一步影响材料的晶格热导率。该利用表面声学声子的角分辨BLS光谱研究材料的弹性和热导率尺寸效应的方法,可以推广到其他的二维范德瓦尔斯材料,这将对于纳米器件的设计加工以及性能优化具有重要意义。同时,相比于原子力显微镜(atomic force microscopy, AFM)和光学衬度测量,显微BLS光谱提供了一种新的非接触的光学方法来评估超薄膜的厚度和残余应力。
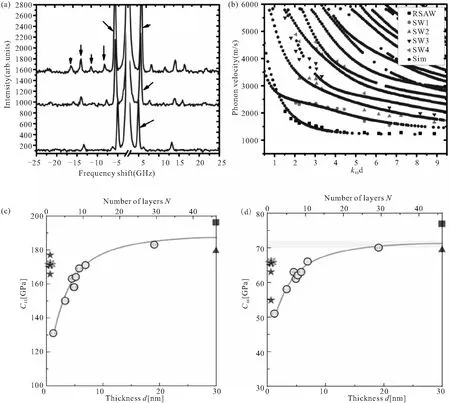
图4 角分辨BLS光谱研究薄膜和二维范德瓦尔斯材料的弹性和热学性能的相关示意图及实验结果。(a)不同入射角下100 nm厚Ge2Sb2Te5薄膜的BLS光谱,展示了瑞利表面声学波(RSAW)和多阶Sezawa波(SW)[24];(b)Ge2Sb2Te5薄膜中沿[100]方向传播的声学声子的声速色散曲线,其中横坐标对应平行于薄膜表面的声子波矢大小和薄膜厚度的乘积(k‖d),实心圆圈对应模拟的数据[24];2H-MoSe2的弹性常数(c)C11和(d)C66随薄膜厚度d(层数N)的变化曲线[28]。圆圈对应Babacic[28]等人工作的实验数据,星形符号对应该文章引用的其它文献中的单层理论计算数据。对于块体2H-MoSe2的弹性性质,图中的阴影面积和三角形、方形符号分别对应该文章[28]的实验数据以及其引用的其它文献中的理论数据。图中的实线为辅助线
4 结论与展望
本文主要介绍了角分辨布里渊光散射(BLS)的基本原理、如何利用BLS光谱得到声速等物理量以求解材料的弹性常数和晶格热导率等参数,以及角分辨BLS光谱在研究块体、薄膜和二维材料的弹性和热学性能中的应用。除了块体材料,无损的角分辨BLS光谱还可以探测到低维材料的元激发,为评估超薄膜的厚度和残余应力,研究晶体的弹性和热学性能的尺寸效应提供了一种新思路。角分辨BLS光谱的测量不仅可以在常温下进行,还可以在低温、高温高压等环境下进行,研究材料的弹性和热学性能与温度和压力的关系,这将有利于对器件稳定性以及服役特性的深入理解和调控。同时,角分辨BLS光谱也将成为研究不同维度材料中丰富的声子相关现象的一项重要技术。
致谢:论文作者张俊感谢国家重点研发计划(2017YFA0303401),中科院创新交叉团队,国家自然科学基金(12074371)对本文论的支持。
