较强海流中的低速水下机器人路径优化

朱心科，侯 斐，孟 肯，罗建超

（自然资源部第二海洋研究所海底科学重点实验室，浙江 杭州 310012）

以水下滑翔机为代表的低航速水下机器人由于长续航力方面的优势，在海洋观测中的应用越来越多。从1997年开始，美国就开始了自主海洋采样网（Autonomous Ocean Sampling Network，AOSN）试验，试验中使用了17个水下滑翔机，其中12个为Slocum水下滑翔机，5个为Spray水下滑翔机，分别搭载温盐深（Conductivity，Temperature，Depth）、叶绿素、荧光计等传感器对蒙特利海湾（Monterey Bay）上升流进行了40天的调查[1-4]。丹麦的卑尔根大学（University of Bergen）利用3台水下滑翔机在格陵兰岛海域对大西洋与北欧之间的海水交换问题进行长期观测[5]。BOSSE A等[6]利用水下滑翔机对Lofoten海盆的涡旋进行连续15个月的观测，对其造成的海洋生态环境参数动态变化进行了记录。然而水下滑翔机的长续航力是以牺牲滑翔速度为代价的，一般来说水下滑翔机的速度为0.5～1 kn，在较强的海流环境中，很难完成设定的观测轨迹。SOULIGNAC M等[7]设计了SWE（Symbolic Wavefront Expansion）算法，在机器人出发时间窗内选择最佳的出发时刻，使得完成使命的时间最短。

水下机器人（Autonomous Underwater Vehicle，AUV）路径规划问题一直是研究的热点，涌现出了各种各样的方法。传统的AUV水下路径规划是以安全为主要出发点，目的是AUV在执行任务的过程中，能够成功避开障碍物或者危险区域[8-10]。随着AUV智能性的提升，AUV路径规划研究的目标除了避障之外，还要考虑任务的完成质量，例如AUV在较强的海流环境中完成指定的任务花的时间最短、走的路程最小、消耗的能量最少或者几种的折中。ALVAREZ A等[11]以完成任务消耗的能量为优化准则，采用动态规划的方法，在不同空间尺度的海流环境中对AUV的路径进行优化。A*算法也常被用作AUV的路径规划[12-13]。

传统的AUV路径规划算法中，一般假设海流为常值，不随时间和位置发生变化，而在实际的海流场中，海流是时空变化的。KRUGER D[14]等设计了优化算法克服了快速变化的双向潮汐流，能够让AUV“骑”着海流穿梭运动，克服远大于自身速度的海流速度。对于以水下滑翔机为代表的低航速水下机器人来说，为了提高续航力必须降低功耗，一般不安装测流速传感器，无法实时获得海流信息。海流预报模型输出的数据可以用来指导水下路径规划。THOMPSON R等[15]依据海流预报数据，利用Wavefront算法设计了在时变海流情况下的水下滑翔机路径规划策略，取得了不错的效果。

对于海洋预报来说，海流的预报时间是有时限的，只能够提供一定时间内的海流预报，而且预报准确度随着预报时间增长而降低[4]。对于利用海流预报数据进行水下路径规划来说，走完从出发位置与目标位置之间路程花费时间有可能超过单个预报周期。本文将针对较强海流场中海流的时变性以及预报周期有限的问题，以水下滑翔机为例，开展低航速水下机器人路径规划方法研究。

1 问题描述

一般情况下，水下滑翔机进入稳定滑翔状态后，浮力调节系统不再发生变化。因此，滑翔速度的大小为定值，滑翔方向是可变的。假设水下滑翔机在稳态滑翔时速度为vr，海流速度为vc。

当k≫2时，海流速度对水下滑翔机的运动轨迹影响微乎其微，路径规划可以忽略海流影响；当k＜0.5时，由于水下滑翔机的速度太小，在海流场中基本上处于随波逐流的状态，失去了路径规划的意义；当0.5≤k≤2时，海流对滑翔机的运动轨迹会有较大的影响，但通过合适的路径规划算法，滑翔机能够克服、利用海流，从而获得一条最优的观测路径，论文针对这种情况开展研究。

论文基于水平面内的二维海流为假设前提。在二维的离散空间，海洋环境定义在n×p个规则的网格上，空间中任意点x=（h，k）为其中的一个网格，0≤h≤n，0≤k≤p，h和k分别代表该网格的横、纵坐标。从出发点S到目标点D的路径P定义为一组有序点的集合Γ=S，…，xi-1，xi，…，D中相邻两点之间的连线。

水下滑翔机在静水中的对地水平滑翔速度为vr，海流速度为vc（x，y，t），表示在t时刻位置（x，y）处的海流速度。以水下滑翔机以最短的时间到达目的地为路径规划目标如下。

2 水下滑翔机运动模型

假设水下滑翔机在静水中的水平滑翔速度为vr，大小为定值，方向可变；海流速度为vc（x，y，t）（在不致混淆情况下，用vc，表示），那么水下滑翔机的对地速度v如下。

海流方向为θc，水下滑翔机静水中的速度方向为θr，对地速度方向为θ。假设二维空间中每个网格中海流速度是定值，如果从一个网格运动到另一个网格，水下滑翔机有8个方向可选，如图1所示。因此，水下滑翔机的对地速度可以写为

图1 可移动方向

由于水下滑翔机速度方向是可变的，可以是任意值。通过式（4）和式（5）消去θr可得关于对地速度的方程如下。

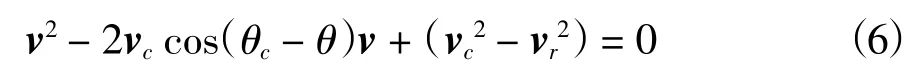
由式（6）表示的方程可以判断滑翔机能否从一个网格运动到另一个网格。若方程有一个正数解，表示水下滑翔机能够从当前网格运动到下一个网格；如果方程的解为有负数或者复数，表示水下滑翔机无法抵制强海流从当前网格运动到下一个网格。如果有两个正数解，选择较大的v作为水下滑翔机的合速度。

3 路径规划算法

对于离散空间中的路径规划问题，Wavefront算法和A*搜索是较常用算法，分别应用这两种算法对水下滑翔机进行路径规划，并对结果进行比较。

3.1 Wavefront算法

传统的Wavefront算法[6]主要分为两个部分，首先，从出发点开始向相邻节点扩展，一直扩展到目标节点为止，在扩展的过程中，记录每个被扩展到的节点需要的代价；然后，从目标节点开始，根据记录的每个被扩展到节点的代价，利用爬山法反向构建最优路径。在这里，进行两个方面的改变：①代价最小的节点优先向前扩展。②每个节点指定一个唯一的父节点。通过修改扩展规则，可以大幅度减小节点的扩展数量，同时有利于反向构造最优路径，提升算法速度。Wavefront算法的扩展过程如下。

（1）A→B，其中A为父节点，B为子节点，表示为P（A，B）。每个节点前向扩展过程中可以有多个子节点，但只能有一个父节点；

（2）T（A，B）表示从水下滑翔机节点A运动到节点B花费的时间；T（B）表示从水下滑翔机出发点运动到节点B花费的总时间；

（3）如果B的父节点为A，即P（A，B），如果满足T（B）＞T（C）+T（C，B），则B的父节点由A改变为C，即P（C，B），并且从出发点运动到B点的花费的总时间更新成T（B）=T（C）+T（C，B）；

（4）每次前向扩展总是从min{T（x）}的节点开始，直至到达目标节点；

（5）从目标点开始，按照代价最低原则反向寻找自己的父节点，直至到达出发点为止。

利用Wavefront算法进行路径规划时，只要从出发点到目标点的路径存在，就一定能够找到一条全局最优路径。但是，由于Wavefront算法无启发式搜索，搜索的过程中扩展的节点较多，因此搜索时间较长。

3.2 A*算法

A*算法与Wavefront算法最大不同之处是代价评价函数中加入了启发函数。启发函数体现了当前节点与目标节点的关系，因此能够加速朝着目标节点方向进行搜索。

A*算法的评价函数定义如下。

式中，T（n）为出发点运动到当前节点的代价；h（n）为当前节点运动到目标节点代价的估计值。

式中，s（d，n）为当前节点到目标节点的欧氏距离；vmax为水下滑翔机的最大速度。当h（n）≤h*（n）（h*（n）为当前节点到目标节点代价的真值）时，h（n）称作可采纳启发函数。在这种情况下，只要从出发点到目标点的路径存在，那么A*算法就一定能搜索到全局最优解。

与Wavefront算法相比，由于A*算法具有启发性，评价函数中体现了当前节点与目标节点之间的关系，只要保证启发函数是可采纳启发，那么在节点的扩展过程中，只需要朝着当前评价函数最小的节点扩展而无需扩展当前节点所有的相邻节点，就能够搜索到全局最优解，从而提升了搜索效率。

3.3 算法仿真

3.3.1 海流模型

以流函数描述的周期性变化的双曲流为例验证路径规划算法[4]。双曲流定义如下。

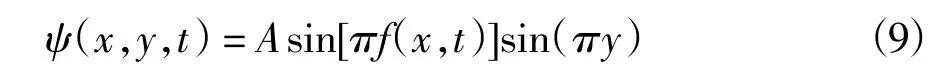
其中，

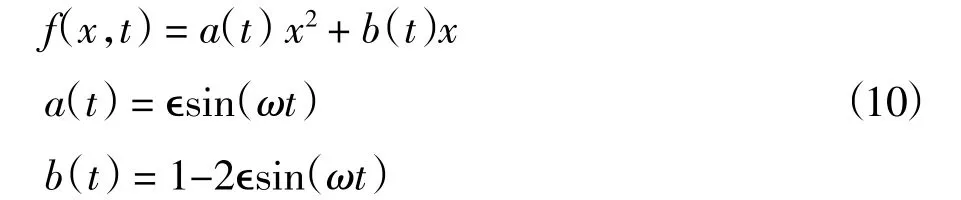
海流的速度场如下。

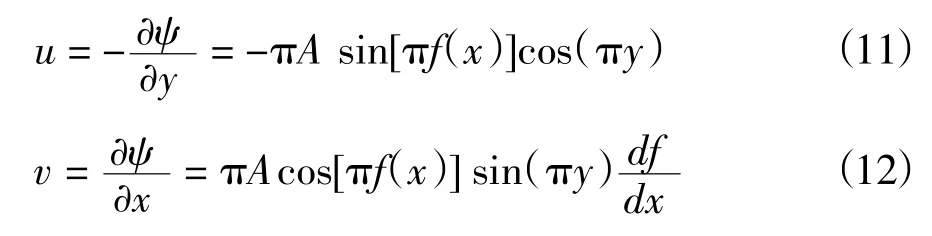
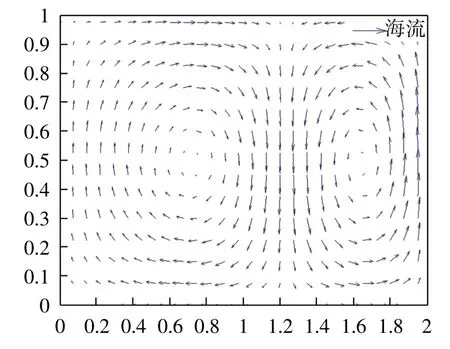
图2 双曲海流

3.3.2 仿真结果

假设在路径规划过程中，已经通过海洋预报获得了海流信息。路径规划的出发点为s（10，20），目标点为d（80，30），分别利用Wavefront算法和A*算法在对水下滑翔机在海流环境中进行路径规划，结果如图3所示。

图3 路径规划结果

图3 （a）中，棕色网格表示Wavefront算法在搜索过程中父节点没有发生过改变，黄绿色网格表示该节点的父节点发生过改变，二者共同表示在算法搜索过程中扩展到的节点。图3（b）中，棕色网格表示A*算法在搜索过程中该节点没有被反复搜索过，黄绿色网格表示该节点被重复搜索过。从图3可以看出，A*算法搜索过程扩展的节点个数明显小于Wavefront算法，从而搜索速度相对较快。在本仿真实例中，A*算法的搜索速度是Wavefront算法的3倍。由于A*算法的启发函数是可采纳的，因此和Wavefront算法搜索到的路径完全一样，都是最优的。

4 分段路径规划

4.1 分段路径规划算法

数值海洋预报根据预报的范围和空间分辨率不同，预报的时效也不同，从数小时到几十个小时不等。当出发点与目标点间的距离相对较近时，完成观测任务需要的时间相对较短，根据单个周期的海洋预报提供的海流信息，利用Wavefront算法或者A*算法均可搜索到最优路径，称之为完整路径规划；当两个点距离较远，单个预报周期提供的海流信息不足以完成观测任务的路径规划时，就需要根据预报周期分段进行路径规划，称之为分段路径规划[4]。

Wavefront算法不适合分段路径规划，因为只能得到出发点到目标点之间的最优路径，无法得到中间值。对于A*算法来说，算法具有启发性，能够评价中间点和目标点之间的相互关系，因此，适合用来进行分段路径规划。

当观测时间超过海流预报周期时，可以利用A*算法先找到单个预报周期内最优的路径，然后再以这条最优路径的终点作为下一段路径优化的起点进行路径规划，直至到达目标点为止。算法伪代码如表1所示。

表1 分段路径规划伪代码

4.2 仿真结果

路径规划算法的海流环境仿真参数同3.1节中的参数，水下滑翔机的出发点为S（170，60），目标点为D（10，20），分别用完整路径规划算法和分段路径规划算法两种方式进行。进行分段路径规划时，假设海流的预报周期为1个时间单位，即10个时间步长的海流预报，仿真结果如图4所示。

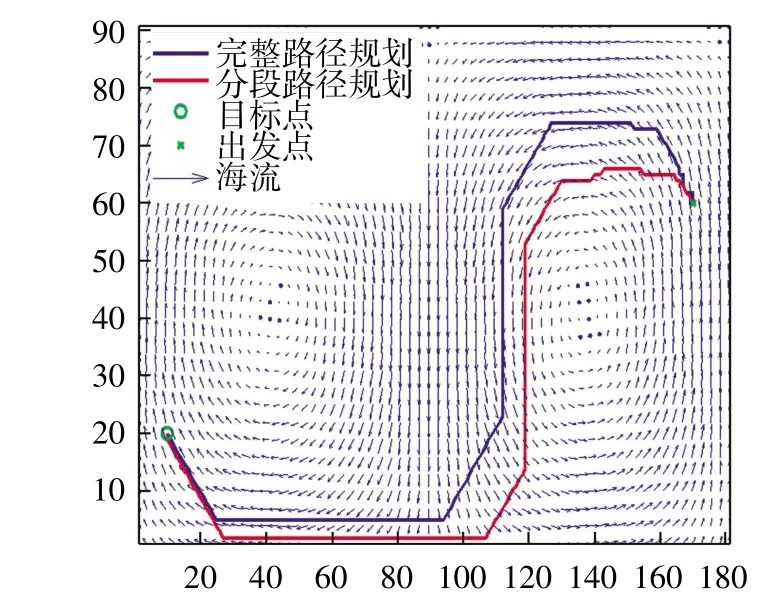
图4 完整路径规划与分段路径规划比较

结果显示，无论是利用完整还是分段路径规划算法，水下滑翔机都能克服海流从出发点顺利到达目标点，二者的差别主要体现在走完该段路径用时不同。完整路径规划得到的路径长度为2.19个距离单位，从出发点到目标点用时5.25个时间单位；分段路径规划得到的路径长度为2.25个距离单位，用时5.73个时间单位。对比发现，分段路径规划获得路径长度仅比最优路径多了2.7%，而用时却多了9%。这是由于基于A*算法的分段路径规划算法是“贪婪”式搜索，当启发函数是可采纳的情况下，每段的路径都是最优的，但是组合起来后就不一定是全局最优；同时，由于两种算法规划出来的路径不同造成滑翔机遭遇到的海流速度（方向和大小）也不同，因此增加的耗时与路径长度并不一定成正比。但总的看来，走完分段路径规划得到路径需要的时间仅仅超过最优路径需要时间的9%，这个偏差结果在可接受的范围之内，表明基于A*算法的分段路径规划算法能够满足时变海流中的低航速水下机器人的路径规划。

5 结论与展望

5.1 结论

针对以水下滑翔机为代表的低航速水下机器人航迹易受海流的影响问题，研究了在较强海流下路径规划方法。

（1）当海流预报周期小于滑翔机水下观测时间时，Wavefront算法和A*算法均能够克服较强海流对滑翔机观测路径的影响，获得最优的观测路径。

（2）当海流预报周期超出滑翔机水下观测时间时，Wavefront算法只能得到出发点与目标点之间的最优路径，而无法得到中间值，无法进行路径规划。

（3）设计了分段式A*路径规划算法，解决了观测时间超出海洋预报周期问题。

仿真结果显示，分段式A*路径规划算法获得较为合理的观测路径。该方法可为水下滑翔机为代表的低航速水下机器人在海洋观测中的应用提供理论指导。

5.2 展望

分段路径规划的本质是“贪婪”式规划，每一段都选择当前的局部最优。局部最优组合起来的完整路径往往与全局最优路径会有一定的差距，未来将会考虑用拉格朗日相干结构（Lagrangian Coherent Structures，LCS）指导路径规划。LCS描述了流体的平均运动，与变化较快的海流场相比，LCS具有长期的稳定性，而且能将海流场明显地分为不同的区域，水下机器人沿着LCS能够较容易地从一个区域到达另外一个区域。同时，水下机器人沿着LCS运动一方面能够节省能量，另一方面也能够提高对地速度，是一条比较理想的轨迹，在最大程度上减小与全局最优解的偏差。基于LCS的路径规划算法对被动式海洋观测设备，如Argo浮标、表面漂流浮标的投放位置、间距的选择也有一定的指导作用，可以避免设备在海流作用下过早地漂到近岸或者聚集在一起，失去大范围观测的意义。