基于传感器阵列多目标优化的SP-QPSO算法研究

孔宇航，陶 洋，梁志芳

(重庆邮电大学通信与信息工程学院，重庆 400065)

0 引言

电子鼻系统又称仿生嗅觉系统，通过模仿生物嗅觉系统的工作原理从而检测目标气体[1]。当有气体经过电子鼻系统时，其中传感器阵列中的某些传感器会产生物理变化，传感器检测到这种物理变化后将其转换为电信号，从而产生特定的特征或者气体印记。经过一系列数据处理后，应用现有的智能模式识别方法实现气体的识别[2]。其中，对广谱化合物产生响应的传感器阵列是关键组成部分，传感器阵列的响应直接决定了模式识别系统的输入质量。在检测待测气体前，由于不清楚哪些传感器对识别结果影响较小，所以初始阵列中会尽可能选取不同特性的传感器。这会造成某些传感器的广谱响应特性产生冗余信息[3]。其次，传感器数量过多将导致后续数据处理爆发“维数灾难”[4]。如何选取对最终识别气体有最大帮助的传感器组合，即经过传感器阵列优化后，将有效地提高电子鼻系统检测结果的识别精度，同时满足电子鼻系统的微型化和智能化的需要。

近年来电子鼻阵列优化的研究方法不断涌现。针对医疗伤口检测中等待时间长、操作过程繁琐等问题，Yan Jia提出了一种结合支持向量机的粒子群优化算法[5]，该方法大大提高了伤口感染细菌的分类准确度，最终实现传感器阵列和分类器参数的同步优化。Sun Hao通过搭建30个气体传感器构造一个电子鼻系统同样用于伤口细菌检测中常见的金葡萄球菌、大肠杆菌和铜绿假单胞菌[6]，采用wilks统计的方法，分别使用直接选择法和逐步选择的思想选择或剔除无用传感器，在保证识别精度同时，有效地减小了传感器阵列的规模。Chang Meizhuo等人利用15个气体金属氧化物传感器检测不同品种的茶香[7]，使用基于聚类分析及区分性能值的气敏传感器阵列筛选方法，通过聚类分析验证各传感器的独立性，选取区分性能值较大对应的传感器，最终得到最优的传感器阵列保证了整个电子鼻系统的输入质量，有效地识别出6个不同品种的龙井茶。

本文首先通过聚类分析预估传感器阵列的大小。再将传感器灵敏度的特性即选择性和多样性作为传感器信息度量的标准，构造两个目标函数。改组复合体演化算法用于构建复合体并监测种群维数的变化。量子行为粒子群优化算法用于每个复合体在搜索空间中的演化。其中，采用自适应的惩罚函数处理约束优化问题将更易于求解。最后，通过支持向量机对优化后的传感器子集进行分类和验证。

1 基于改组复合体演化量子行为粒子群优化算法相关原理

1.1 多目标优化函数构造

一般情况下，选择灵敏度高的传感器可以提供关于每种气体所包含的最多的相关信息。但传感器相互之间往往存在交叉敏感特性，即它们的敏感气体之间不可避免地存在着交叉和重叠，很容易产生冗余信息。另外，对于每种气体，其响应模式由阵列内所有传感器的灵敏度决定，传感器灵敏度的差异性越高，其模式区分越明显。所以同时也将传感器灵敏度的差异性作为影响阵列优化的因素之一。

假如存在区分N类待测气体的分类任务，初始阵列中传感器数量为M，优化后的传感器数量为K（K≤M ），把全部的传感器灵敏度Sij构成一个初始矩阵[8]。构造两个关于传感器特性的目标函数。目标函数1是由灵敏度矩阵中列的信息熵组成，对于传感器 j，其选择性越高，灵敏度矩阵第j列的熵值就越小。目标函数 2是由灵敏度矩阵中行的信息熵组成，对于气体i，其差异性越大，灵敏度矩阵第i列的熵值就越小。

以传感器选择性构造目标函数1：

（1）计算第 j列中元素的总和，并对Sij归一化处理：

其中i和 j分别表示气体类别和传感器，j的值在优化过程中动态确定。

（2）计算每个选定传感器j的信息熵：

（3）获取N类气体分析物获得的最大信息熵：

（4）K个基于信息熵的传感器选择性的目标函数1：

同理，N个基于信息熵的传感器差异性的目标函数2：

以上两个目标函数的值都在[0,1]范围内，最小化这两个目标函数将分别获得传感器最大的选择性和多样性。在多目标优化过程中使用这两个目标函数，所得的传感器阵列将得到最相关的信息。

1.2 约束优化

在求解多目标优化问题时通常涉及约束优化的情况，所以如何平衡约束优化和目标函数是一个重要的难题[9]。在目标函数中加入惩罚项，该函数一般由惩罚参数乘以违反约束的度量组成，进而使约束优化问题转化为无约束优化问题[10]。

给定n维解X，其中 X = (x1, x2,… ,xm)，将M个目标的约束优化问题定义为：

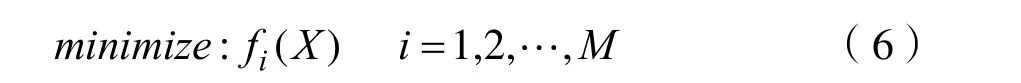
常见的惩罚函数模型是由目标函数与惩罚项之和组成，二者共同构成了适应度函数。其中X到可行域距离称为违反度，其违反度函数表示为：

其中F(X)是适应度函数，f(X)是目标函数，j是约束条件个数， j = 1 ,2,… ,J 。kj是个体在约束 j上的惩罚系数，vj(X )是个体在约束 j上的违反度。

对公式（7）中惩罚项的参数进行改进，采用一种自适应惩罚函数，即在优化过程中动态调整惩罚系数：

其中 f( xi)代表当前种群中目标函数的平均值， vj(xi)表示当前种群中 j个平均约束违反度的大小，N是种群大小。

结合构造的目标函数公式（4）和（5），则整个种群的适应度函数为：

在计算出每个解的约束违反程度和适应度值之后，根据约束支配规则，在任意两个候选解之间选择非支配解。

1.3 改组复合体演化算法

在高维空间中可能存在某些问题，例如“维数灾难”，这严重影响了高维空间算法的执行效率。最早解决高维空间问题的单纯形作为一种局部搜索算法[11]，但是粒子可能会收敛到原始搜索空间的一个子空间，后续的演化将被限制在子空间内，并且几乎无法恢复到原参数空间中的完全搜索，这种现象称为“种群退化”。有研究学者提出了主成分分析的改组复合体演化算法（Shuffled complex evolution with PCA with University of California, Irvine, SP-UCI）用于解决上述“种群退化”问题[12]。它的原理是如果算法通过数据集丢失了n个维度，则最后有n个主成分上的数据投影方差等于零。通过沿主成分以零方差添加新的数据点来帮助恢复丢失的维数。SP-UCI算法中的点在搜索空间中呈随机分布，所有的点存储在数组 D = { xi,fi, i = 1 ,2,… ,s}，其中 fi是xi对应的函数值。经过初始化后，将种群数组D划分m个复合体 A1, A2, …,Am，每个复合体包含p个点。复合体的具体表现形式为：

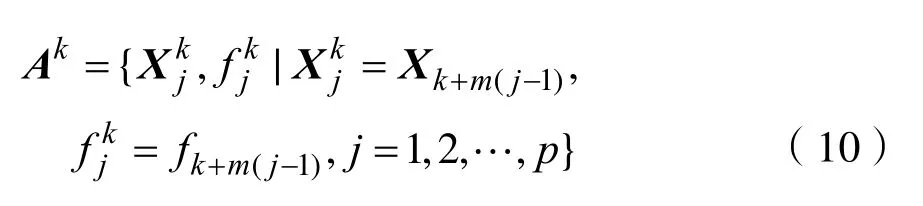
在每次迭代中，将复合体采用改组的方案，即把复合体之间以一种共享获得信息的方式来构造新的复合体。在每个阶段中，存储在数组中的复合体都要排序和替代。经过改组和构造的新复合体会不断地再生，直至满足最终的条件。

利用 SP-UCI策略有助于算法检查和监控维数的变化，避免“种群退化”，并确保在优化过程的开始就访问搜索空间中的所有区域。

1.4 量子行为粒子群优化算法

量子行为粒子群优化（Quantum behaved Particle Swarm Optimization，QPSO）是一种量子模型概率化粒子群优化算法[13]。它的原理是将粒子的寻优过程看作势场中粒子向势能最低点移动的过程。QPSO算法不仅提高了原始PSO算法的全局收敛能力，而且更易于算法的实现和参数的选择。该算法的计算公式为：

其中α作为收缩-膨胀系数用来控制算法的收敛速度， α = 0 .5 + 0 .5(T - t )/T ，T是总迭代次数，t是当前迭代次数。

1.5 列文伯格马夸尔特算法

列文伯格-马夸尔特算法（Levenberg-Marquardt，LM）是众多最优化算法中比较有效的一种方法[14]。它的原理是假设初始数据点附近存在可以信赖的最大位移s，以s为半径所划分的区域内，寻找目标函数的一个近似最优点，从而求解得到发生的位移。计算目标函数值后，假如其下降的范围达到了一定条件，则继续按照该规则迭代求解下去；如果没有达到这一条件，则相应的减小一定位移的范围，然后重新计算求解。LM 优化算法有助于SP-QPSO算法加快收敛速度，保证所有粒子向最优解的方向移动。

基本的LM优化算法的定义为：

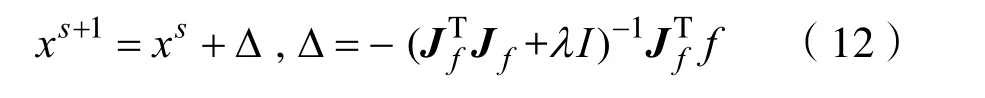
2 基于改组复合体演化量子行为粒子群优化算法

为了提高算法在高维空间优化问题的性能，提出了一种 SP-UCI算法和 QPSO算法混合的算法SP-QPSO，即基于改组复合体演化量子行为粒子群优化算法（Shuffled complex evolution with PCA-Quantum behaved particle swarm optimization,SP-QPSO）的传感器阵列多目标优化研究方法。使用 1.1章节中构造的两个关于传感器特性的目标函数，以求函数最优值为优化目标。下面详细介绍提出的SP-QPSO算法，算法的全流程步骤如算法1所示。

算法1SP-QPSO算法的全流程步骤

基于改组复合体演化量子行为粒子群优化算法

输入：初始化种群大小，最大迭代次数等参数；

输出：非支配Pareto解集；

过程：

Step.1初始化m个复合体，每个复合体中包含p个点，采样大小为s=m*p，样本的维数d，搜索空间为 X1, X2,… ,Xs。

Step.2在搜索空间中初始化种群的大小。计算每个点的函数值，根据函数值对这些点进行排序，并存储在数组 D = { Xi,fi, i = 1 ,2,… ,s}。

Step.3对高维空间中的特征进行维数检查。如果存在“种群退化”现象，检查出丢失的维度并恢复。

Step.4将数组D划分为m个复合体，Ak=

Step.5使用QPSO分别进化每个复合体kA，每个复合体寻找其最优函数值。

（1）初始化种群大小N和最大迭代次数T。

（2）在复合体 Ak中建立一个包含N个点的子集群计算其函数值，并将其存储在，其中 Yik是粒子，vik表示函数值。

（3）通过比较搜索空间中所有局部最优位置找到最优值，并将其分配给全局最优值。

（4）为下一次迭代计算种群的平均最优位置mbest以及粒子向全局最优值移动的位置。

（5）重复上述过程，直到满足最大迭代次数或者停止标准为止。

Step.6多正态重采样检验陷入局部最小值的概率。

Step.7复合体重新改组，将 A1, A2,… ,Am替换成一个数组并对其进行排序。

Step.8重复上述过程，直到满足停止标准为止。

Step.9群体最优位置转化为对应Pareto最优子集。

3 实验验证与分析

3.1 数据集介绍

本文中，数据集来自加州大学圣地亚哥分校实验室[15]，由8个MOX金属气体传感器组成的气体传感器阵列采集。传感器的型号类型详细信息如下：R1:TGS2611 R2:TGS2612 R3:TGS2610 R4:TGS2600 R5:TGS2602 R6:TGS2602 R7:TGS2620 R8:TGS2620。数据集由100个时间序列的片段组成，每个片段都是一次归纳或背景活动，总计919438点。该传感器阵列长期放置于家庭中，数据集包含3种共100个不同条件的时间序列：葡萄酒、香蕉和背景活动。其中包括葡萄酒的36种响应记录，香蕉的 33种响应记录，背景活动的31种响应记录。

3.2 实验设置

本文的实验环境为MATLAB R2016a。提出的SP-QPSO算法中，初始粒子种群设置为20，最大迭代次数为1000，粒子维度为30，在搜索空间中随机初始化粒子位置。所选的分类器是基于径向基函数的SVM，核参数和惩罚因子均采用默认值。

3.3 实验结果分析

传感器阵列中某些响应之间存在相关性，这些传感器提供的信息之间可能存在冗余。首先通过聚类分析中的离差平方和方法分析该数据集的相关性，通过欧式距离评估传感器大致可分为几类，分析潜在的传感器最优组合的数量，从而为确定最终阵列中传感器的数量提供参考依据。SPSS Statistics 20软件对该过程进行分析，所得的结果用树状图表示，如图1所示。

由图1可知，该数据集涉及的这8个气体传感器大致分为4组：A组（传感器S1和S3），B组（传感器S2），C组（传感器S4、S7、S8），D组（传感器 S5、S6）。每组类别中传感器的信息非常相似。这说明了某些传感器的响应之间的确存在共线性。因此，最优传感器阵列可能需要 4个左右的传感器数量以区分目标气体。

图1 数据集通过聚类分析得到的树状图Fig.1 dendrogram obtained by cluster analysis of the data set

然后利用提出的 SP-QPSO算法通过数据集验证，运行10次后的结果如表2所示。表中信息包括Pareto解集的数量、运行10次时间的平均值、运行成功次数。结果表明传感器阵列大小为3、4、5、6时，均存在Pareto最优解集，其余情况下不存在 Pareto解集。当传感器阵列大小为 5时，Pareto解集的数量有最多的13个，此时的平均运行时间最长。同时由于该算法存在不稳定的因素，在约束优化中加入惩罚函数后，实际仅出现了 2次运行失败的情况。并且Pareto解集大部分集中在传感器阵列大小为4个左右，有效地验证了采用聚类分析对数据集的初步分析。

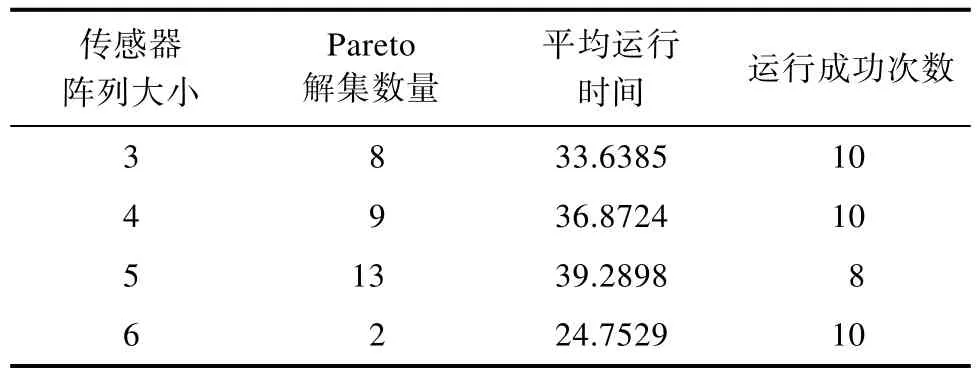
表2 SP-QPSO 算法运行实验结果Tab.2 the running experiment results of SP-QPSO algorithm

利用传感器灵敏度的选择性和差异性这两个特性，构造了两个目标函数，其传感器阵列大小为3、4、5、6时的Pareto解集分布如图2所示。可以看到图中Pareto集合中非支配解的数量并不总是随着最佳阵列大小而增加。Pareto优化解的个数随着阵列大小先增加后减小，传感器阵列大小为3时存在8个Pareto解集，传感器阵列大小为4时存在9个Pareto解集。当阵列中传感器个数为5时，存在13个最多的Pareto解集。而当阵列中传感器数目为6时，仅存在2个Pareto解集。因此Pareto解集主要取决于解决方案的分布，而不是优化阵列大小。

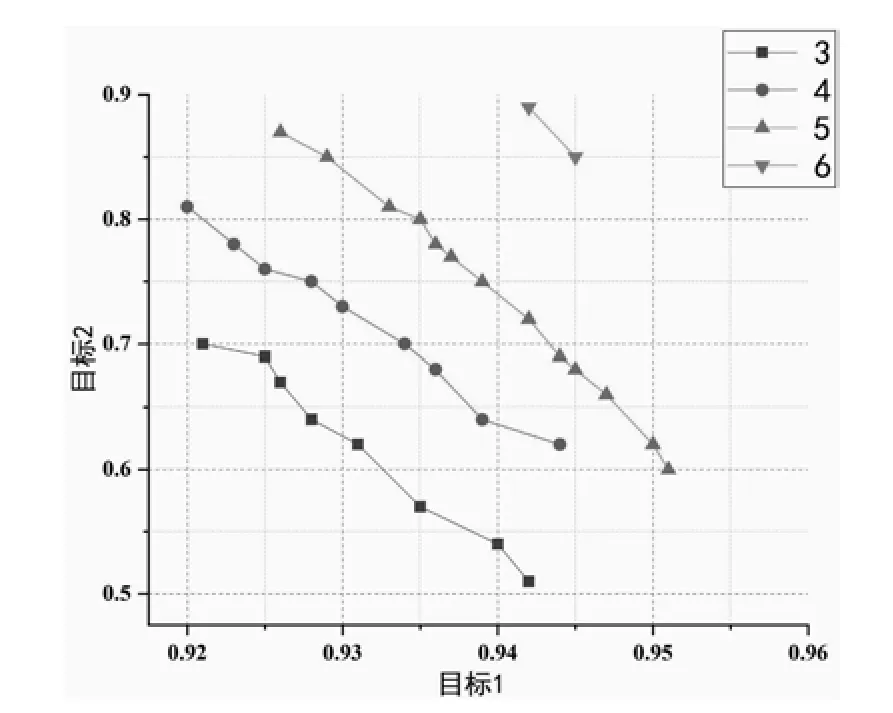
图2 优化后不同阵列大小下Pareto优化解的个数Fig.2 the number of pareto optimization solutions under different array sizes after optimization

为了准确地验证本章提出的基于 SP-QPSO算法用于电子鼻传感器阵列多目标优化。在单目标优化和多目标优化两种场景下，将粒子群优化算法（PSO）、带权重的粒子群优化算法（SPSO）、量子行为粒子群优化算法（QPSO）作为对比算法，随机选取各自优化后的10组Pareto解集，其中单目标优化仅使用传感器选择性的特性构造的目标函数1，然后采用支持向量机SVM对数据集中3类目标气体的响应值进行分类，观察分类结果。各算法的分类精度如表3所示。

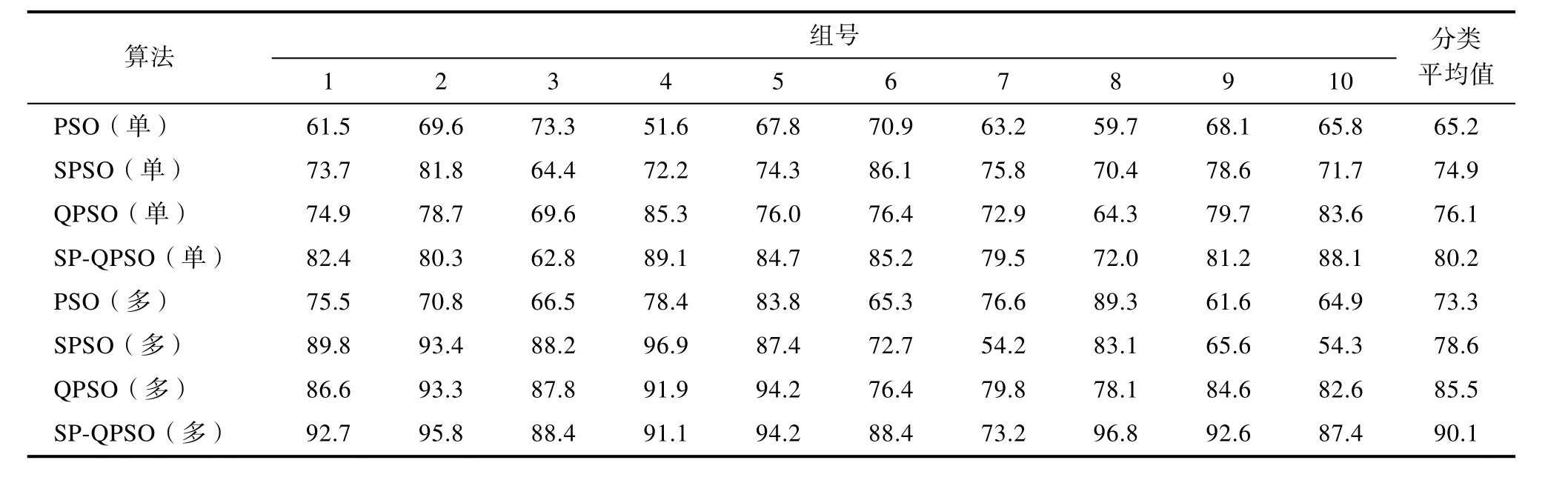
表3 不同算法场景下单目标和多目标优化后的结果(%)Tab.3 results of single objective and multi-objective optimization in different algorithm scenarios (%)

可以看到在单目标优化场景下，SP-QPSO算法的平均分类精度最高，达到了 80.2%。该算法在10组的Pareto优化解中，有6组取得了更好的分类精度。同样在多目标优化场景下，SP-QPSO算法在全部的对比算法中平均精度最优，达到了90.1%，有 7组 Pareto解对应的传感器组合取得了更优的分类精度。即该算法验证了在高维样本空间中处理约束优化问题的优势。为了更直观地反映各算法在阵列优化的分类能力，不同算法下在单目标和多目标场景优化后的对比图如图3所示。此外，这些算法的分类精度均高于初始阵列传感器组合的分类精度，充分证明了本次阵列优化的有效性。而且不论何种算法，多目标优化场景下算法取得的分类精度明显优于同类算法单目标优化场景下的分类精度，即多目标优化保证了电子鼻传感器阵列拥有更好的输出质量。

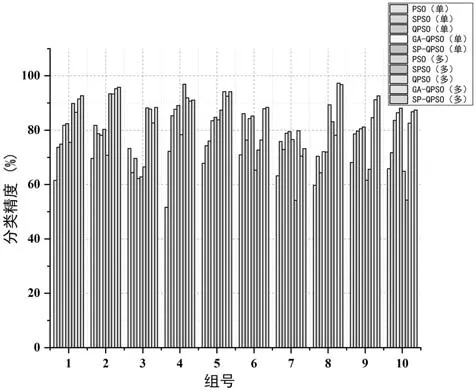
图3 不同算法下单目标和多目标优化后的对比图Fig.3 comparison of single objective and multiobjective optimization with different algorithms

4 结论

在高维空间中，传感器阵列优化过程在一定程度上为后续的数据处理带来“维度灾难”，同时可能存在“种群退化”的现象。提出了一种基于改组复合体演化量子行为粒子群优化算法（SPQPSO）的传感器阵列多目标优化研究方法。该方法具有以下特点：（1）SP-UCI算法用于构建复合体并监测种群维数的变化，QPSO算法用于每个复合体在搜索空间的演化。（2）引入自适应惩罚函数计算搜索空间的违反度，以指导搜索空间可行区域的求解。实验仿真结果表明，SP-QPSO算法在多目标优化场景下算法具有更好的分类精度，这对传感器阵列优化过程中高维空间产生的数据处理后的效果更好。这充分验证了基于SP-QPSO算法地传感器阵列多目标优化研究的有效性，最终用较少数量的传感器构建了高质量的阵列。