炸药粉末压制工艺参数对药柱质量的影响

曹 兴，赵捍东，曹红松，张程健，刘恒著，吴宗娅，熊瑞红

(1.中北大学 机电工程学院，山西 太原 030051；2.山西江阳化工有限公司，山西 太原 030041)

引 言

聚能破甲战斗部药柱常采用粉末压制成型工艺制备，该工艺将以HMX为基的塑料黏结炸药通过模压法在真空中压装成型[1]，药柱成型密度、均匀性以及回弹量影响战斗部的毁伤威力。为保证发射安全性及撞击目标时的作用可靠性，成型药柱必须保证密度的相对均匀。粉末压制过程中，温度、初始密度、压制速率等工艺参数影响炸药粉末压制成型质量，传统炸药粉末压制工艺[2-3]通过检测炸药最终成型密度、回弹量来判断药柱质量的好坏，借助实践经验不断调整工艺参数、改进压制模具以及压制方式，但这种方法成型后的炸药粉末质量难以保证。

目前，随着计算机有限元技术的发展，金属粉末压制成型模拟已被用于工艺参数的优化，而对于炸药粉末压制成型模拟也有学者进行了探索。张涛等[4]对高聚物黏结炸药粉末温压成型过程进行了数值模拟,得到了成型压力对高聚物黏结炸药粉末成型的相关规律。刘群等[5]利用非线性有限元计算方法，对炸药颗粒压制成型过程进行了数值模拟计算，得出在一定压力下，粉末压制过程存在运动和变形两个阶段。以上均是研究压制力工艺参数对炸药粉末压制成型的影响，而针对压制速率以及初始密度对炸药粉末压制成型的影响未见报道。

本研究以聚能装药战斗部为背景，利用高级非线性有限元软件MSC.Marc建立JO-9159炸药粉末药柱压制成型的连续体计算模型，模拟了炸药粉末压制成型过程，得到了压制速率、初始密度对相对密度的影响规律以及在压制过程中炸药粉末位移变化规律。

1 有限元建模

目前，大多数学者针对粉末压制成型过程的力学模型研究都是在基于连续体的假设上进行的，即将粉末材料视为体积可压缩的弹塑性材料，整体上粉末材料遵循质量不变条件，局部粉末颗粒遵循体积不变条件，本研究模拟炸药粉末压制成型过程也是将炸药粉末视为连续体，运用弹塑性力学模型来分析炸药粉末压制过程的相关变化规律。采用更新拉格朗日方法求解炸药粉末压制过程，该过程属于非线性问题，同时，在压制过程中发生了大位移、大变形，而这种方法用于分析非弹性行为导致较大的变形，在分析中，初始拉格朗日坐标系几乎没有物理意义，因为非弹性变形是永久的。

1.1 炸药粉末压制工艺过程

称取一定量的炸药粉末，将其装入模具中，给上模冲施加一定的外力，得到预定要求的炸药高度、密度和一定炸药强度的炸药药柱。图1为炸药粉末压制模具示意图。

图1 炸药粉末压制模具示意图

1.2 有限元网格的初始划分及重划分设置

由于炸药粉末压制时所受的载荷是对称的，同时炸药几何尺寸也是轴对称的，为减小计算量，故简化模型，以其轴线作为对称轴，建立二维轴对称有限元模型。对称轴所在方向为X轴，径向所在方向为Y轴，炸药几何尺寸为半径13mm，粉末初始药高44mm，设置初始相对密度为0.5，并划分网格，设置网格单元尺寸为0.5，图2为粉末压制有限元模型。在模拟计算求解设置中，设置了网格重划分准则，重划分单元数量设置为10000网格。

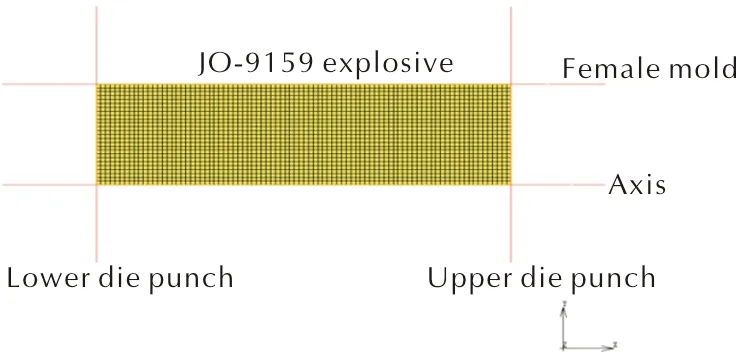
图2 JO-9159粉末压制有限元网格计算模型

1.3 粉末材料本构模型

粉末压制屈服准则采用Shima-Oyane模型[6]。Shima和Oyane提出的粉末屈服准则在粉末成型有限元模拟中获得广泛应用，并被集成到MSC.Marc商业软件中。屈服函数用于表达材料屈服所应满足的函数关系，Shima-Oyane屈服函数分析粉末流动规律和相对密度分布规律，考虑粉末体在变形时的体积变化、流动应力和静水压力对粉末体屈服强度的影响。Shima-Oyane的修正模型数学表达式如下[7]：

(1)

式中：σy为单轴屈服应力；σd为偏应力分量张量；p为静水压力；γ、β为材料参数，为相对密度的函数，一般不为常数。需要通过材料试验确定。由于γ、β不为常数，在实践过程中，一般用如下公式表达：

γ=(q1+q2ρq3)q4

(2)

β=(b1+b2ρb3)b4

(3)

β=ρ5.5

(4)

γ=[6.25(1-ρ)]-0.5

(5)

该数据来源于Marc软件手册所提供的参数初始值，本研究q1、q2、q3、q4、b1、b2、b3和b4的值分别取0、1、1、5.5、6.25、-6.25、1和-0.5。

模拟采用的样品为JO-9159炸药，其密度为1.864g/cm3，屈服强度为30MPa。泊松比与相对密度关系表达式为μ=μ0×E-12.5(1-ρ)2[9],μ0表示致密炸药的泊松比，取值为0.224，ρ为相对密度；弹性模量与相对密度的关系采用线性变化规律E=E0×ρ，E0为致密体的弹性模量，取值为8.4GPa。实际粉末压制过程中，粉末与模具是有摩擦的，摩擦系数在有限元模拟中有着至关重要的作用，而影响摩擦系数的因素有很多，模具表面的光滑度、粉末的相关特性等，总体来说，摩擦系数是随相对密度变化的，但文献未有对摩擦系数的专门研究，因此，本研究不考虑摩擦对结果造成的影响，假设摩擦系数为定值0.2。

1.4 边界条件及模拟设置

边界条件定义了控制冲头的运动状态，添加控制点，利用控制点控制冲头运动；设置初始条件，初始相对密度为0.5；模拟粉末压制成型的实际过程共设置了加载工况、保压工况以及卸载工况；收敛判据选择残余力或位移，收敛容差设置0.1。

2 压制成型过程模拟及结果分析

在压制速率0.2m/s时，分析炸药粉末在压制过程中位移、相对密度、回弹量以及模具的受力变化情况。

2.1 压制过程中粉末位移变化规律分析

图3为炸药粉末总体位移变化云图及轴向和径向位移云图。由图3(a)可知，粉末压制最终成型高度为21.72mm，压制成型过程中，靠近上模冲的一侧，炸药粉末位移最大，且从上到下呈递减的趋势，呈阶梯分布，其最大位移为22mm；在下模冲与炸药粉末接触的区域，炸药粉末发生的位移最小，量级在10-2；在粉末压制卸载过程中，炸药位移有减小的趋势，即发生了回弹，回弹量为0.28mm。

图3 炸药粉末总位移、轴向和径向位移变化云图

由图3(b)和(c)可知，轴向发生的位移最大，径向的位移最小，这表明粉末流动方向主要为轴向流动，揭示了粉末压制成型的流动规律，这也验证了张涛等[4]在PBX粉末成型的数值模拟研究中得到的结论：粉末压制过程主要为轴向流动。

图4为选取初始粉末不同轴向位置等间隔取点作为采样点的示意图。图5为不同径向位置在同一时间所对应的轴向位移。

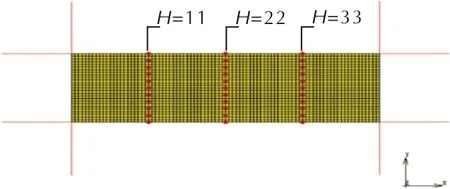
图4 采样点位置示意图

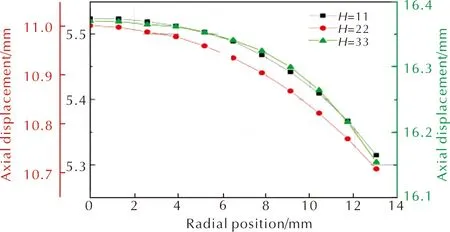
图5 轴向位移随径向位置变化规律

由图5可知，不同轴向位置，粉末径向位置同一时间所对应的轴向位移具有相同的变化规律：炸药粉末与模套接触的侧壁粉末位移较轴线处小，由此可以得出在炸药粉末压制成型过程中，靠近阴模的区域，炸药粉末流动缓慢，在轴线区域，炸药粉末流动较快，这是由于在阴模附近，炸药粉末颗粒与阴模有较大的摩擦力,从而造成阴模附近粉末流动缓慢。

2.2 相对密度变化规律分析

粉末压制成型后，相对密度变化云图见图6。从图6可以看出，相对密度变化分布不均匀，平均值在0.97以上。进一步提取不同径向位置处相对密度随轴向位置变化数据，即Y值为0、6.5、13mm处的相对密度变化数据，如图7所示，图7(a)为提取的相对密度变化数据，图7(b)为利用origin软件对提取出的数据点进行拟合的样条曲线。

图6 相对密度变化云图

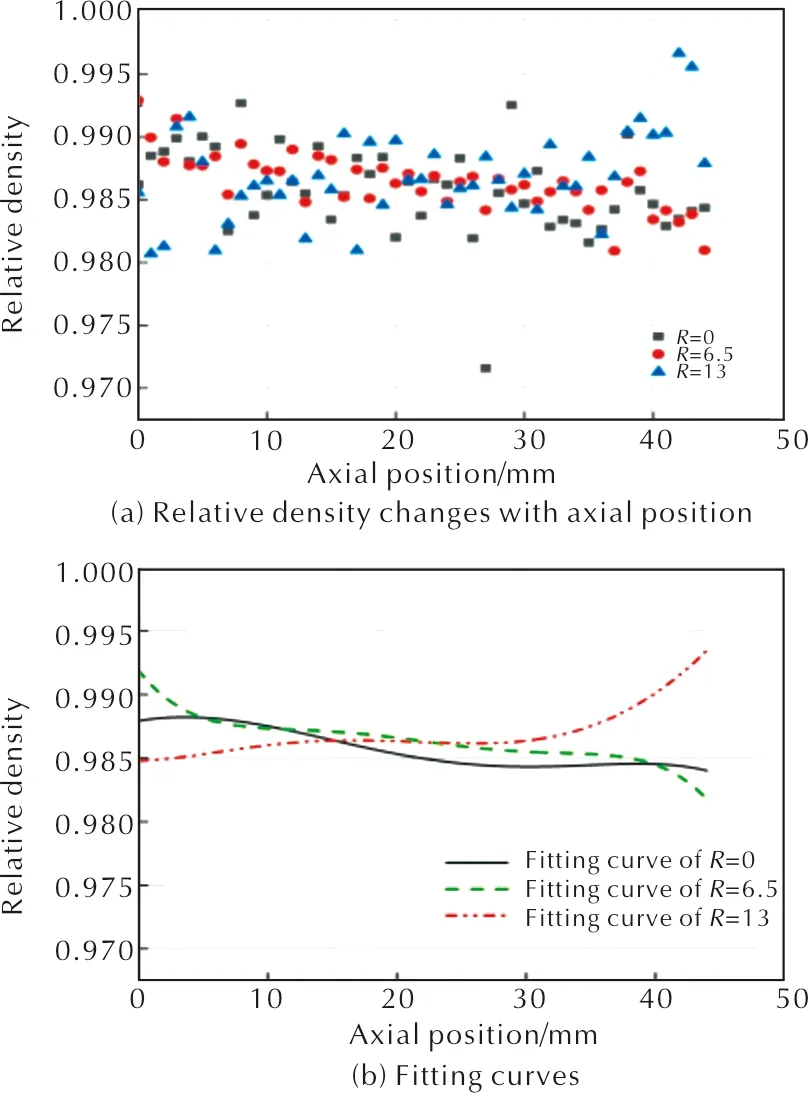
图7 不同径向相对密度随轴向位置变化规律

从图7中可以看出，靠近上、下模冲的区域炸药粉末的相对密度较高，在中间区域，其相对密度数值较低，在0.982～0.990范围之内。总体来看，靠近阴模区域的相对密度值要大于其他区域的相对密度值。

利用工业CT检测系统对成型药柱进行切片检测，结果见图8。由图8可知，炸药粉末压制成型后，不同区域密度分布有差异，但差异不明显。通过对成型药柱切成若干块进行密度测试，其水平密度差约为0.3%，基本符合粉末压制成型模拟结果，也证明粉末压制成型采用Shima-Oyane模型是可行的，建模是成功的，模拟结果可以为炸药粉末压制工艺提供参考。

图8 成型药柱切片CT检测图

2.3 压制过程阴模及模冲的受力影响分析

模冲与阴模受力大小影响模具的寿命，图9为模具的受力曲线。

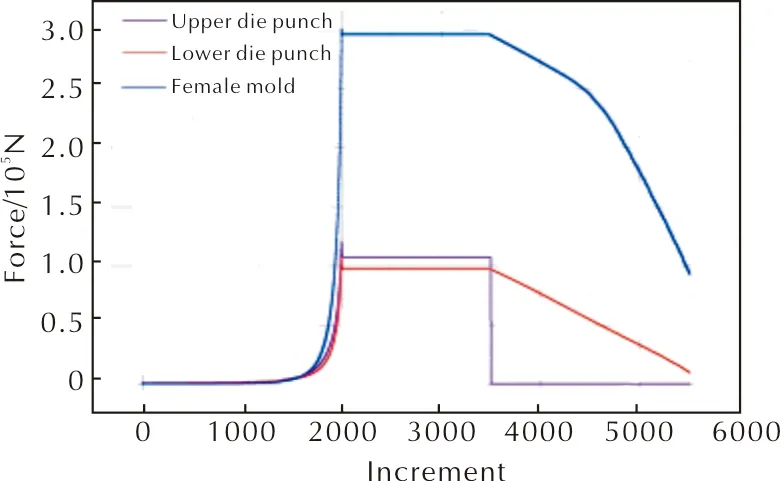
图9 模具受力曲线

由图9可知，在加载过程，上、下模冲以及阴模受力变化规律相同，呈指数分布，这是由于压制初期，炸药粉末处于松散状态，到接近致密体时，炸药粉末内部阻力增大，为使其达到设定的高度，便需要较大的力推动，且阴模的受力大于上、下模冲的受力，其阴模最大受力为3.0×105N，上模冲最大受力为1.1×105N，下模冲最大受力为1.0×105N；在保压过程，上、下模冲以及阴模所受到的力保持不变；在卸载过程中，上模冲的力瞬间减小，下模冲力的减小呈线性变化，对于阴模受力先缓慢减小，后期减小加快。因此，可以为模具的设计提供以下建议：由于阴模受到的作用力较大，上模冲次之，下模受到的力最小，因此，在制作模具时，阴模材料的选择可以选择强度高的材料，冲头可以选择强度较小的材料，这样可以降低材料成本。

2.4 工艺参数对压制成型药柱质量的影响

为了研究工艺参数对炸药粉末压制成型的影响，分析了不同压制速率和初始相对密度对炸药粉末压制成型的影响。压制速率选取210、220、230、240和250mm/s，初始相对密度选取0.6、0.7和0.8。

2.4.1 压制速率对相对密度的影响

图10和图11分别为相对密度及其差值随不同压制速率的变化曲线。

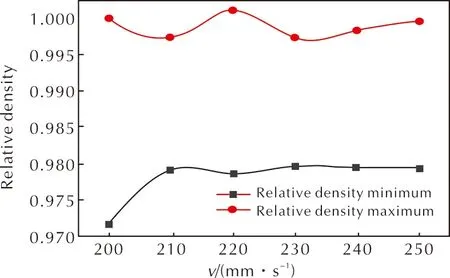
图10 相对密度随不同压制速率的变化曲线

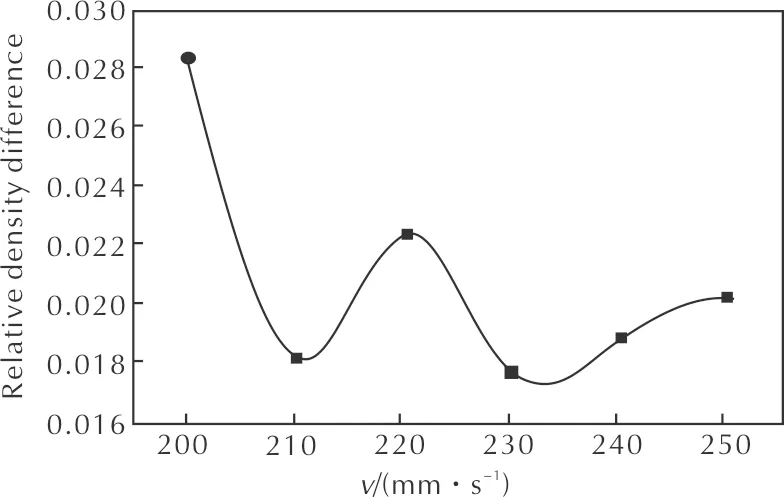
图11 相对密度差值随不同压制速率的变化曲线

图12为不同压制速率下的相对密度分布云图。分析不同压制速率下相对密度变化情况发现，提高压制速率有助于提高相对密度值，改善粉末致密性，且随着压制速率的提高，相对密度显著提高，压制速率提升到一定程度，相对密度值变化趋于平缓。分析图12可知，随着压制速率的提高，粉末相对密度变得更加均匀。

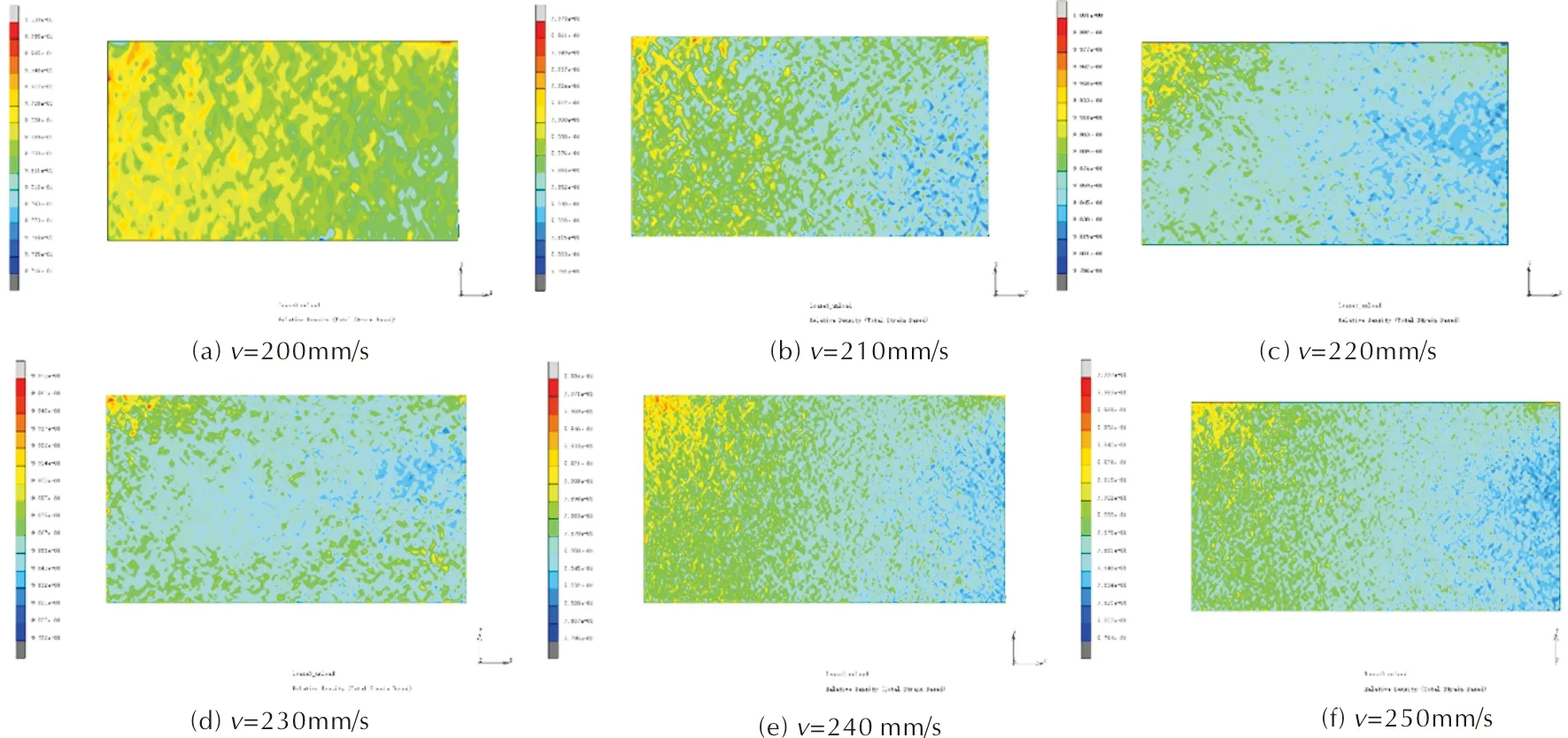
图12 不同压制速率相对密度变化云图

2.4.2 压制速率对回弹量的影响

回弹量影响炸药药柱的装配以及炸药的成型密度。绘制回弹量随压制速率变化曲线如图13所示。由图13可知，随着压制速率的增加，回弹量也在增加，最大值为0.3mm，最小值0.27mm。压制速率在200～220mm/s内，回弹量逐渐增加；压制速率在220～230mm/s内，回弹量趋于稳定；压制速率在230～240mm/s，回弹量又逐渐下降；压制速率在240～250mm/s内，回弹量又逐渐上升，且在压制速率为240mm/s时，回弹量达到最小，为0.27mm。综上所述，结合不同压制速率对相对密度的影响，在所选压制速率范围内，最优的压制速率为240mm/s。

图13 回弹量随不同压制速率的变化曲线

2.4.3 不同初始相对密度对相对密度的影响

图14为相对密度随不同初始相对密度变化曲线。分析曲线发现,最大相对密度随初始相对密度先增加后降低，最小相对密度随初始相对密度先下降后上升。由此可见，初始相对密度在0.5～0.6时，粉末压制效果最好。随着初始相对密度的增加，等效米塞斯应力下降。增大初始相对密度，即增大松装密度，有助于提升粉末压制成型后的密度，降低等效米塞斯应力。

图14 相对密度随不同初始相对密度的变化曲线

3 结 论

(1)采用高级非线性有限元软件MSc. Marc，借助Shima-Oyane粉末材料模型可以较好地模拟炸药粉末压制成型过程，粉末成型后密度分布情况与实际相符合。

(2)粉末压制流动方向主要为竖向流动，且粉末与模具接触区域流动较轴线处移动缓慢。粉末压制成型后，粉末相对密度随压制速率呈非线性变化，在压制速率为240mm/s时压制效果最好。

(3)粉末压制成型过程中存在回弹量。压制速率为240mm/s时，粉末成型后回弹量最小。回弹量与压制速率没有固定的规律，整体上看，压制速率大，回弹量较大。

(4)初始相对密度对粉末压制成型有一定的影响，初始相对密度的提升有助于提高粉末成型后的相对密度。