应急医药物资实物与产能混合储备研究
2021-03-07陈建华刘仁勇
陈建华,刘仁勇
(南华大学 经济管理与法学学院,湖南 衡阳 421001)
20世纪以来,突发公共卫生事件的频繁来袭给我国带来了难以估量的损失。从2003年SARS到2009年的甲型H1N1猪流感,再到2020年初的新型冠状肺炎(COVID-19),都给人们的生命健康和财产安全等产生了巨大的威胁,也对我国的经济以及社会等方面造成了极大地破坏。据国家统计局统计数据显示,受新冠肺炎疫情冲击,2020年第一季度,我国GDP为206 504亿元,按不变价格计算,比上年同期下降6.8%;也有学者指出在新冠疫情发生后,由于医疗物资需求暴增,使得供应严重短缺,进而造成市场主导的医疗物资供给机制失灵[1]。因此,为保证公共卫生事件发生后应急医药物资能够有效地供给,减少其所造成的损失,提高应急医药物资的储备管理水平显得极为重要。
目前我国应急医药物资的储备方式主要为政府单独储备,虽然这种储备方式能够及时地满足物资的突发需求,但仍存在采购和管理成本高、巨额资金占用以及因管理不善造成医疗物资浪费等问题。同时受储备空间及物资保质期的限制,此方式下物资的储备数量较低且品种偏少,往往难以有效满足政府的应急需求。因此,面对当前应急医药物资储备的难题,有关学者认为提高社会代储水平是解决政府单独储备模式弊端关键而有效的途径。Zhang等对政府应急物资储备情况进行归纳,指出应急医药物资的主要储备方式为企业代储[2]。皮武良对当前我国医疗应急物资储备机制进行分析,指出政府需要激励和引导企业参与应急医药物资储备中[3]。在应急医药物资储备方式方面,张永领在层次分析法的基础上,指出各类应急物资应当采取不同的储备方式,其中应急医药物资的储备要以合同储备和生产能力储备为主[4]。宋劲松等提出政府不要局限于单一的实物储备模式,可以选择与药品物资流通企业、生产企业以及医院等达成合作[5]。沈兵等认为政府加大储备量的同时还要委托企业扩大应急产能,储备必要的医疗物资应急生产线[6]。上述研究主要是应急医药物资储备方式的定性分析,虽然十分强调政企合作储备的重要性与必要性,但是并没有量化政企合作过程中的储备量分配,无法为政企双方合作的开展提供具体的指导依据。
对此,许多学者对应急物资的储备量分配进行深入探究。陈业华等从政府总成本最小化的角度出发,给出了政府实物储备以及企业生产能力储备的最优储备方案[7]。此外,也有学者从供应链的角度出发,利用供应链理论对政企双方的储备数量展开研究。部分学者基于实物期权契约分析政企联合储备模式,对政府与企业双方的最优储备量进行探究[8-11]。田军等则是从实物储备扩展到生产能力储备,并以期权契约为基础对生产能力储备量等问题探讨分析[12-13]。在政府与单一企业联合储备模型的基础上,刘阳等从政府与多个企业合作储备的角度出发,建立政企多方联合储备应急物资模型,并给出了政企多方的最优储备量[14-15]。Coskun等从委托企业储备的角度,通过两个合作代储企业之间的博弈来确定两者的最优应急物资库存数量[16]。虽然上述研究对应急医药物资储备进行了定量化的分析,为政企合作提供了一定的指导依据,但有关应急物资库存持有成本均假定是线性的,该假设虽然在储备数量较小的变化范围内可以近似成立,但在储备量的变化范围较大的情况下则有偏于现实情况,无法表示出企业在储备应急医药物资过程中的实际储备成本。对此,Goh和Giri等认为库存持有成本是关于库存量的非线性成本,且其边际成本是库存量的单调递增函数[17-19]。唐小我和官建成利用多项式函数来表示一般非线性成本模型,并指出可以采用拟合法或插值法得到确切的非线性成本函数[20-21]。
基于此,本文在应急物资联合储备模型[7,22]的基础上,从非线性库存成本角度出发,通过对应急医药物资实物储备与产能储备的成本进行分析,构建了应急医药物资实物与产能混合储备模型,并给出了不同条件下政府委托两类不同企业的最优储备量。综上可以看出,本文的研究不仅为政府应急医药物资的储备工作提供实践指导,也为构建多企业参与的政府应急医药物资储备体系提供了理论支撑。
一 问题描述与变量说明
(一)问题描述
目前应急医药物资的储备方式主要有政府单独储备以及与委托企业进行共同储备等。政府单独储备,即政府提前采购物资放置于仓库,但由于政府的库存管理水平较低,政府单独储备的成本一般要高于相关企业的储备成本。为了更合理地利用资源,政府会选择委托相关企业储备来提高物资储备水平,实物储备与产能储备是企业代储的主要储备方式,实物储备模式主要是由仓储企业提高安全库存来保障应急医药物资储备水平,而产能储备模式则是由生产企业扩大产能来达到提高应急医药物资储备水平的目的。政府会以成本最小化为目标,通过分析比较两种方式的储备成本对储备量进行最优分配。
(二)符号说明
Q:应急医药物资数量,其中Q0表示突发公共卫生事件引起的应急医药物资实际需求量;P:应急医药物资价格;e:应急医药物资相关原材料价格;hi:仓储企业的应急医药物资库存持有成本相关系数;ω:应急医药物资单位生产设备价格;L:生产设备的残值;t:生产设备的使用期限;S:单位时间单位生产设备折旧费用;q:单位生产设备的产能;k:总产能储备下的原材料储备比例;h:生产企业的单位原材料的库存持有成本;H:生产企业储备产能的固定成本;T:政府委托企业储备的时间期限;r:企业的投资回报率,其中r1和r2分别表示仓储企业和生产企业的投资回报率。
二 模型构建
(一)应急医药物资的实物储备成本
在考虑政府与仓储企业展开合作时,即委托仓储企业提高安全库存来提高应急医药物资储备水平,仓储企业视应急医药物资库存为常规库存物资,对物资进行实时更新,动态保持应急医药物资储备量不变。此时提前储备的物资依旧属于仓储企业,仓储企业实际储备成本主要包括:库存持有成本以及资金占用成本。
有关库存持有成本的核算,本文认为企业储备时间期限T内的医药物资的物资库存持有成本与储备量有关,视为储备量的多项式函数:
h(Q)=h0+h1Q+h2Q2+…+hn-1Qn-1+hnQn
其中,n为正整数,hi表示库存持有成本相关系数(i=0,1,2,...,n)。而具体函数形式需要政府收集企业的实际库存持有成本的相关数据,并运用相关多项式函数拟合方法来得到。基于一般成本函数形式,本文选取n=3来表示企业库存持有成本函数,即设定储备时间T内库存持有成本与库存量的关系为:
h(Q)=h0+h1Q+h2Q2+h3Q3
为了便于后续探讨分析,本文基于实际库存管理过程对相关系数hi进行分析:
(1)因为应急医药物资的库存管理中必不可少的会有一些固定成本,所以h0>0;
(2)因为库存持有成本为库存量的单调递增函数,即当Q≥0时,h′(Q)≥0,所以h1>0;
(3)从规模经济理论出发,边际成本在较低的库存量情况下会随着储备量的增加而降低,这是因为在合适的储备规模内协调规划库存管理工作会提高物资管理效率,从而降低平均成本和边际成本,即实现规模经济;而在较高的库存量情况下,随着库存量的增加,库存管理的各个方面难以协调,需要投入额外的成本来维持库存管理活动,所以此时边际成本为库存量的递增函数,即表现为规模不经济。故其边际成本随着库存量的增加而先降后增,则有:h″(Q)先小于0后大于0,故有h2<0,h3>0。
有关资金占用成本的核算可以利用企业的投资回报率来表示,其成本公式为:C0=A[(1+r)T-1],其中A表示占用资金。结合应急医药物资的库存持有成本以及资金占用成本,则有仓储企业储备的成本函数为:
Csw(Q)=h0+h1Q+h2Q2+h3Q3+
PQ[(1+r1)T-1]
其中h0,h1,h3>0,h2<0。
(二)应急医药物资的产能储备成本
在考虑政府与生产企业展开合作时,即委托生产企业提升产能来提高应急医药物资储备水平,此时提前储备的设备以及一定原材料依旧属于生产企业,生产企业实际储备的成本主要包括:生产企业设备折旧成本、原材料储备成本、资金占用成本和固定成本。


关于原材料储备成本的核算与前面实物储备的库存持有成本不同,原材料储备是防止突发事件发生后较短时间生产过程中出现物资缺失,故原材料的储备数量是总产能储备量的一定比例k,且原材料的储备数量变化范围不大,因此本文认为其库存持有成本可以近似于线性库存持有成本h,则原材料储备成本表示为:hkQT。
生产企业的资金占用成本包括两个部分,生产设备占用资金和原材料占用资金。综上,则有生产企业储备的成本函数为:
Ccn(Q)=N(Q)ST+hkQT+[ωΝ(Q)+
ekQ][(1+r2)T-1]+H
(三)应急医药物资的最优储备方案
为了实现应急成本最小化,政府会考虑与仓储企业和生产企业多方展开合作,则有政府委托多方企业混合储备的成本函数为:

PQ1[(1+r1)T-1]+N(Q0-
Q1)ST+hk(Q0-Q1)T+
[ωΝ(Q0-Q1)+ek(Q0-
Q1)][(1+r2)T-1]+H
其中Q1,Q2分别表示实物与产能储备量,且Q2=Q0-Q1。由于向上取整函数N(Q)为分段函数,故需要对Q1分区间讨论,比较每个区间的最小值即为总的最小储备成本,对应的储备方案即为最优分配方案。


PQ1[(1+r1)T-1]+N(Q0-
Q1)ST+hk(Q0-Q1)T+
[ωΝ(Q0-Q1)+ek(Q0-
Q1)][(1+r2)T-1]+H
通过对Q1求导可得:
其中G=P[(1+r1)T-1]-hkT-ek[(1+r2)T-1]。
1.当Q0≥c,基于上文中的分析可知,h0,h1,h3>0以及h2<0,则根据G+h1的取值范围可分为三种情况:
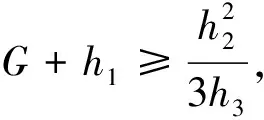

当Q1在[0,Q0-a1q),[Q0-a1q,b],[c,Q0-a2q)以及[Q0-a2q+q,Q0)中任意一个分段区间内有Chh′(Q1)≥0,即Chh(Q1)取区间左端点为区间最小值;当Q1在[b,c]的范围内有:
Chh(Q0-iq+q)-Chh(Q0-iq)=h(Q0-
iq+q)-h(Q0-iq)+Pq[(1+r1)T-1]-
ST-hkqT-(ω+ekq)[(1+r2)T-1]
由于在该范围内Chh′(Q1)<0,且-ST-ω[(1+r2)T-1]<0,可得Chh(Q0-iq+q)-Chh(Q0-iq)<0。故此情况下,Q1=c时Chh(Q1)取最小值。同时考虑Q1=Q0,此时政府的最小储备成本为:min{Chh(0,Q0),…,Chh(Q0-a1q,a1q),Chh(c,Q0-c),Chh(Q0-a2q,a2q),…,Chh(Q0,0)};
(3)当G+h1≤0,即Chh′(Q1)存在两个零点且只有一个零点大于零时,可知在0≤Q1≤c的范围内Chh′(Q1)≤0;在Q1>c的范围内Chh′(Q1)>0。同样假设Q1=c位于A3=[Q0-a3q,Q0-a3q+q)内,其中a3∈i,且不考虑当Q1位于[0,Q0-nq+q)内的情况。基于上述分析则有:Q1∈[0,c],当Q1=c时,Chh(Q1)最小;当Q1在[c,Q0-a3q+q),[Q0-a3q+q,Q0)的任意一个分段区间内有Chh′(Q1)≥0,即Chh(Q1)取区间左端点为区间最小值。考虑Q1=Q0的储备成本,在该情况下政府的最小储备成本为:min{Chh(c,Q0-c),Chh(Q0-a3q+q,a3q-q),…,Chh(Q0-q,q),Chh(Q0,0)}。
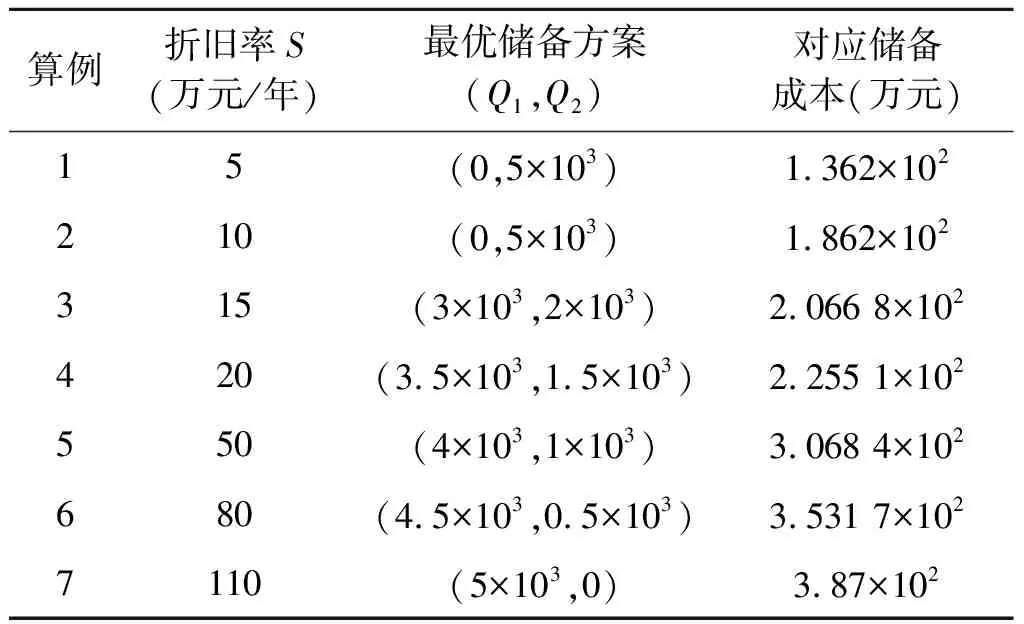
2.当Q0 (3)当G+h1≤0时,基于上文中的分析可得,政府的最优分配方案为(Q0,0)。 本文假设某地区政府预测得到的某应急医药物资的需求量为Q0=5×103单位量,且该地区只有1个仓储企业以及1个生产企业。由于每年储备数量都会进行调整,故政府一般委托企业储备的时间期限T=1年。有关仓储企业有:该物资每年库存持有成本函数为:h(Q)=30 000+1 200Q-0.6Q2+0.000 1Q3,该物资采购单价P=800元/单位,仓储企业投资回报率r1=8%。关于生产企业有:生产设备价格ω为8×105元/台,生产设备折旧率S为1.5×105元/年,单位生产设备的产能q为5×102单位量/年;生产企业储备产能的固定成本H为20 000元/年;原材料储备比例k为0.02,生产企业的单位原材料的库存持有成本h为100元/年,应急医药物资相关原材料价格e为200元/单位,生产企业投资回报率r2=10%。 将上述已知代入相关计算公式,可以计算得出政府选择实物储备需要支付3.87×102万元,而选择产能储备需要支付2.362×102万元。相较于单一储备模式,政府选择混合储备模式并通过合理分配储备量可以减少储备成本,此时的最优分配方案为实物储备和产能储备的储备量分别为3×103单位量和2×103单位量,对应储备成本为2.066 8×102万元,对比产能储备成本减少了12.50%的储备费用。考察生产企业的设备折旧率对最优储备方案以及最小储备成本的影响,其他数据不变,对参数的数量关系分析见表1。 表1 参数数量关系分析表 从上述分析结果可以发现,在其他条件不变的情况下,设备折旧率与政府最小储备成本成正相关,即设备折旧率越大,政府最小储备成本越小,且随着设备折旧率的增加,所得到的最优储备方案也有所变化,其中产能储备数量所占比例越来越小。 本文利用库存成本以及其他成本函数等理论,在借鉴应急物资联合储备模型的基础上,对应急医药物资实物以及产能储备成本进行分析,建立了基于实物储备与产能储备相结合的应急医药物资储备模型,为政府应急医药物资的储备分配方案的制定提供了科学依据,从而可有效促进政企双方常态化合作关系的建立。具体而言,本文主要得到以下研究结论及管理启示: (一)基于多种储备方式下,政府可以通过合理分配对不同储备方式的储备量,大幅度降低政府应急医药物资储备的总成本,为政府在应急储备工作提供参考依据。 (二)应急医药物资的最优储备决策受仓储企业以及生产企业的各项参数影响,同时物资的价格以及生产设备折旧率等因素也对储备分配有一定影响,因此政府在做储备分配决策时要对协议企业以及储备物资进行实践调查与分析。 (三)应急医药物资的实际需求量也对政府的最优分配方案有影响,故政府在进行应急医药物资储备前的分析预测工作也是应急医药物资储备管理中的关键之一。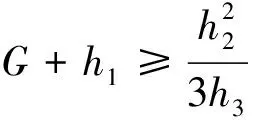

三 数值算例
四 结 论
