基于POD的尾流激励叶片气动力降阶模型
2021-03-07王沐晨李金玖李立州
刘 钊,王沐晨,李金玖,张 珺,李立州
(1.中北大学 机电工程学院, 太原 030051; 2.太原学院数学系, 太原 030001)
保证航空发动机具有较长使用寿命和较强可靠性,一直是现代航空发动机设计过程中追求的目标[1]。在发动机内部动、静叶之间的高速相对转动,使得下游叶片极容易受到周期性的上游尾流激励,诱发下游叶片流场产生周期性振动,进而使得下游叶片表面气动力具有周期性。这种周期性的气动力有可能导致叶片强迫振动,甚至出现严重的疲劳破坏,影响整个发动机的可靠性和使用寿命。因此,研究尾流激励下叶片的气动性能,能为航空发动机叶片的气动优化提供依据,对提高整个航空发动机的质量、使用寿命和可靠性具有重要意义。
近年来,计算流体力学(Computational Fluid Dynamics,CFD)被广泛用于研究叶片气动特性[3-9],然而在工程实践中明显可以看到,CFD技术虽然计算精度高,但其最大的缺陷在于计算时间长,当研究需要反复迭代的问题时,其计算量更为巨大,工程应用很不便。为有效地避免这个问题,Dowell[10]、Silva[11]等提出了基于CFD技术的非定常气动力降阶模型(Reduced Order Model,ROM)。ROM作为一个可以表述非定常流体系统绝大部分动力特性的简化数学模型[12],其计算所消耗的内存、时间和设计周期相对于传统的CFD方法减少了十几个甚至几十个数量级[13]。现有的降阶模型方法有Krylov子空间法、POD法、Volterra级数和谐波平衡(Harmonic balance,HB)等几种[14],其中POD法计算效率和精度较高,在工程上应用范围较广。在流体力学领域,Lumely[15]引入POD方法用来分析紊流场的流动特性,其理论方法是在寻找最小二乘意义下的最优有序正交基。周强等[16]采用POD方法建立了降阶的气动弹性系统状态空间方程,实现了快速预测气弹系统颤振边界。Jian Z等[17]用POD法求解了曲面组合板非线性颤振的运动方程,与CFD/CSD结果吻合良好,节省大量计算时间。
为快速计算上游尾流激励下叶片气动力,采用POD法提取主要降阶基模态,构建基于POD的尾流激励下叶片气动力降阶模型,并对叶片气动力数据重构,实现快速分析上游尾流激励下的叶片气动力。
1 POD降阶基模型建立

(1)
为简化描述,采用矩阵u来表示流场气动力:
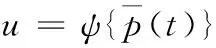
(2)
根据POD理论,可将尾流激励下的叶片气动力分解为平均值和脉动值的叠加[18]:
(3)

(4)
其中,αr为第r个POD基向量对应的模态系数;φr为POD降阶基向量;R表示POD基的个数,选择合适的阶次R就可以得到尾流激励的叶片气动力降阶模型。

图1 叶片气动力系统示意图
1.1 POD降阶基提取
本征正交分解(POD)的原理就是将一个高维向量,通过一组最优正交基投影到一个低阶的向量空间中,保留主要特征,并且可以基本重构出所对应的原始高阶向量。令ui,i=1,2,3,…,N是在N个瞬时提取的流场气动力数据(称为“快照”),可以通过数值模拟或者实验测量得到。POD的目标在于找到一个正交基函数,使得:

(5)

(6)
令U={u1,u2,u3,…,uN},对式(6)求偏导数有:
(7)
令Z=UUT,式(5)求最大值的问题就转化为求POD核函数Z特征值和特征向量的问题:
Zφ=λφ
(8)
对式(8)使用奇异值分解(Singular Value Decomposition,SVD)方法,即可求出Z的特征向量以及特征值λi,i=1,2,3,…,N。定义能量百分比:
(9)
式中I(r)表示前R个特征值占总能量的份额,I(r)越接近1,表示特征向量包含的信息越完整,通常取I(r)=0.99,求得的前R个特征值对应的特征向量就是最终的POD基φr(r=1,2,3,…,R)。
1.2 气动力数据重构
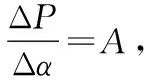
对于任一时刻的尾流输入总压Pr,响应的POD模态系数为αr,则有:
(10)
2 算例分析
二维叶片流场CFD计算模型如图2所示,计算网格采用ICEM输出的非结构网格,网格单元数为164 606,节点数为92 040,叶片网格结构如图3所示,导入Fluent计算叶片气动力,流体定义为理想气体,采用Spallart-Allmaras湍流模型,进口设置为压力进口pressure-inlet。稳态时,进口总压为 120 500 Pa,出口压力101 325 Pa,温度300 K。瞬态计算时,将UDF编译的上游尾流加载在流场进口最下方点,尾流速度大小10 m/s,方向为进口y方向。

图2 叶片CFD计算模型示意图

图3 叶片网格结构示意图
上游尾流输入的进口总压波形如图4所示,设置计算时间t=[0,0.08],时间步长为2e-5 s,进口压力随时间呈现周期性变化,计算可得4 000个进口总压的叶片气动力数据并保存。

图4 周期信号压力波波形
将4 000个原气动力系统的总压数据划分为100个具有相同概率的非重叠区间,从每个区间中按均匀分布随机地抽取一个点,得到100个时刻的叶片表面气动力,作为气动力快照矩阵,对快照矩阵做POD分解,得到100个POD基模态。图5分别展示了样本点计算的CFD结果与已知CFD结果的绝对误差,误差范围分别为[0.01,0.027]与[-0.05,-0.027 5],均在可接受范围内,说明样本点CFD结果的准确度高,可以忽略样本点CFD计算数据对研究结果的影响。


图5 CFD计算结果绝对误差曲线

图6 能量比值随POD模态变化曲线
降阶模型计算结果与CFD计算结果如图7所示。图中,红色实线为CFD计算结果,蓝色实线为POD降阶模型的计算结果。从图中可以看出,降阶模型计算结果与CFD计算结果一致,因此可以采用POD方法构建尾流激励气动力降阶模型。同时CFD计算结果与降阶模型计算结果之间存在一定的误差。
为了评估降阶模型精度,引入了均方根误差RMSE和平均绝对误差MAE,其基本公式分别为:
(11)
(12)
式中:i为第i个计算结果的气动力数据,Oi为POD降阶模型得到的气动力数据,Fi为CFD求解的气动力数据。分别将数据代入式(11)和式(12)可以得到系统的均方根误差和平均绝对误差,如表1。

图7 上游尾流激励下的叶片气动力响应随时间的变化曲线
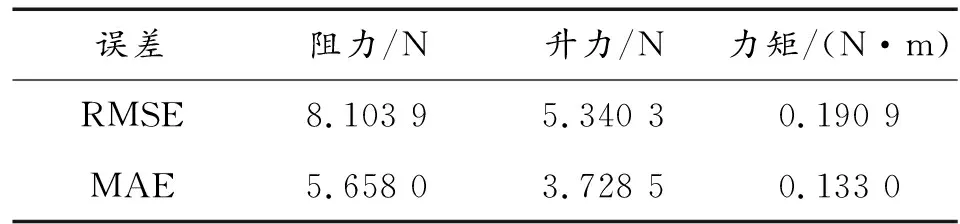
表1 周期信号输入的均方根误差(RMSE)和平均绝对误差(MAE)
由表1可知:误差均在可接受范围内,故叶片气动力降阶模型具有很高精度。
3 验证POD降阶模型
为了进一步说明降阶模型可以计算不同尾流激励下的叶片气动力,将图4中的将尾流压力波换成一组正弦信号波,波形如图8所示,叶片计算的稳态边界条件保持不变,将正弦尾流压力信号输入到下游叶片的入口处,完成CFD计算,得到正弦信号激励下叶片气动力数据。
将压力信号数据直接输入到已经建立的叶片气动力降阶模型,得到叶片气动力响应值并保存,所得计算结果与CFD计算结果如图9所示。利用POD计算结果和CFD计算结果,得到降阶模型的均方根误差和平均绝对误差,如表2。
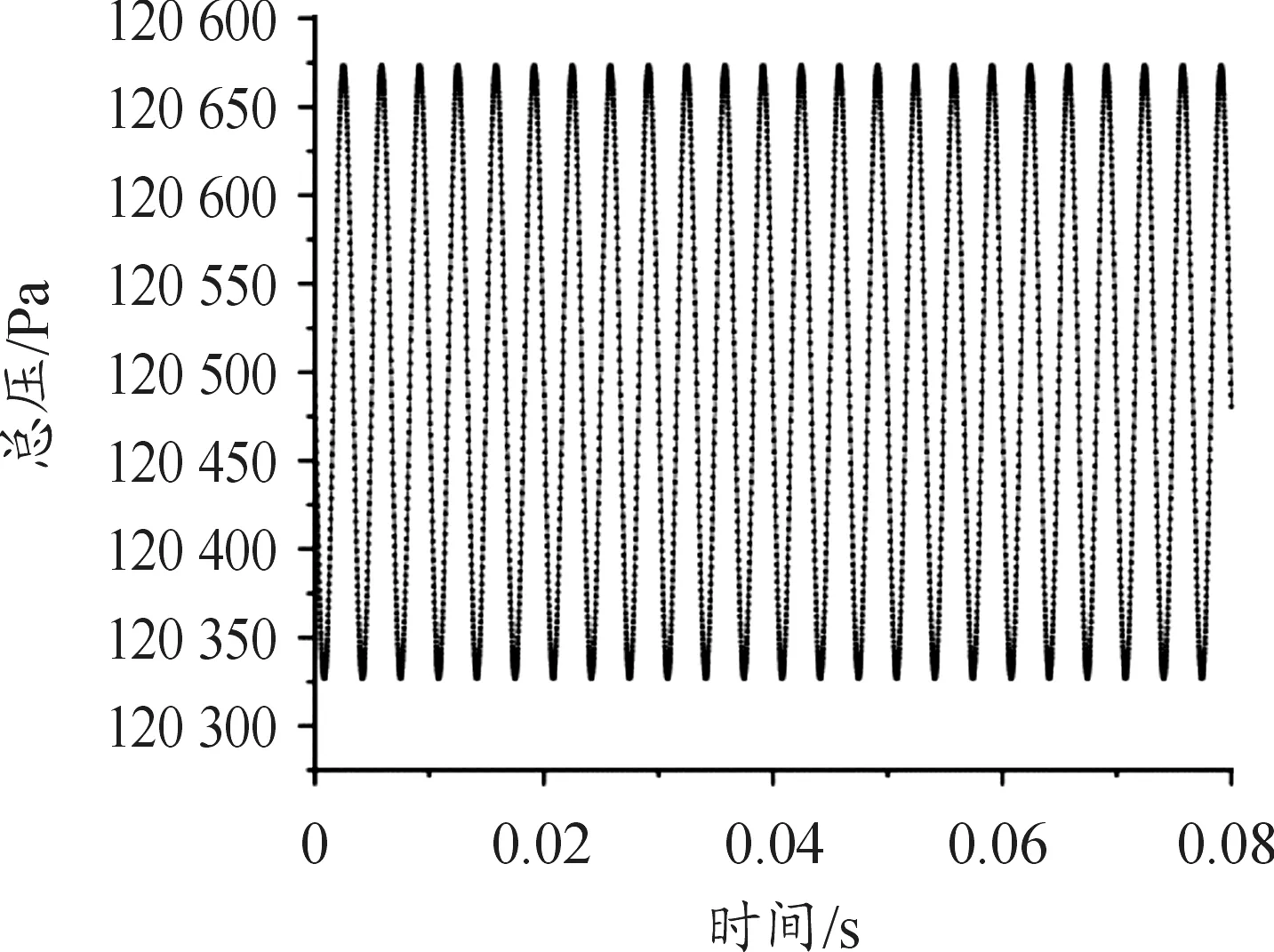
图8 正弦信号压力波波形图
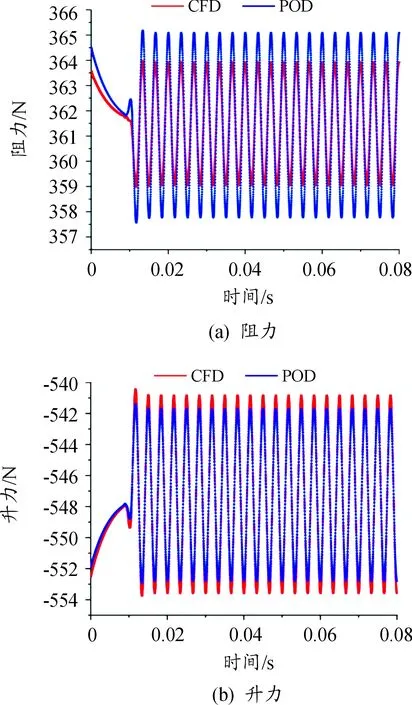
图9 游尾流激励下的叶片气动力响应随时间的变化曲线

表1 正弦信号输入的均方根误差和平均绝对误差
对于本文第二次输入的正弦信号,图9(a)、图9(b)分别为POD降阶模型和CFD输出的阻力和升力的对比图。从图中可以得出,POD降阶模型与CFD求解结果一致。误差数值基本在0左右波动,进一步说明降阶模型的准确性。
对比表1和表2数据可知,两组输入状态下,降阶模型精度相差10倍,差异较大的原因是输入尾流的振幅不同。由于叶片气动力系统为弱非线性系统,算例中选择的稳态压力值为120 500 Pa,周期信号的振幅为[-5 000 Pa,1 000 Pa],正弦信号的振幅为[-175 Pa,175 Pa],振幅越小弱非线性特征越明显,精度越高。综合表1和表2的数据,阻力、升力和力矩最大平均绝对误差分别为5.658 0、3.728 5和0.133 0,误差均满足要求,说明当输入尾流信号稳态值一定,振幅不同时,基于POD方法建立的尾流激励状态下叶片气动力降阶模型可以用于叶片气动力快速分析,表明基于POD方法的降阶模型具有实用性和可行性。
4 结论
1) 当更换输入的压力信号以后,POD降阶模型与CFD计算结果误差很小。
2) 本文建立的POD气动力降阶模型能快速准确的分析上游尾流激励下的叶片气动力。
3) 尾流输入的稳态值一定时,尾流压力振幅影响叶片气动力降阶模型精度。
