基于加权相似性度量的特征匹配方法

胡立华，左威健，聂瑶瑶

（太原科技大学计算机科学与技术学院，太原 030024）

（*通信作者电子邮箱sxtyhlh@126.com）

0 引言

特征匹配是建立来自同一物体的两幅图像间特征点的可靠对应关系，现已广泛应用于汽车驾驶、目标跟踪、即时定位与地图构建（Simultaneous Localization And Mapping，SLAM）［1-2］、视觉导航、三维重建［3-4］等领域。但是由于采集图像受环境、时间、摄像机角度差异、传感器不同等问题的影响，易产生以下问题：1）采集的图像存在大量噪声；2）采集的图像畸变情况严重。因此，如何精确、稳定地查找特征点之间的对应关系是计算机视觉中的一个传统而关键的问题。在特征匹配过程中，图像特征点之间的相似性度量标准是影响特征匹配结果的关键因素之一，因此，如何有效地定义特征点之间的相似性度量标准是提高特征匹配效率的关键问题。

目前，特征间的相似性度量标准的设计主要取决于应用场景的选择。不同场景的相似性度量方法［5］主要包括三类：基于距离相似性的度量方法、基于图像相关的相似性度量方法以及其他的度量方法。典型的基于距离相似性度量方法［6］有：Zhao等［7］提出了一种改进的Hausdorff距离算法，适用于像素值较少的灰度图像，可有效处理噪声图像匹配；Wang 等［8］采用棋盘距离与城市距离的线性组合替换欧氏距离，在提高匹配精确率的同时还减少了算法的运行时间；Kang 等［9］采用部分Hausdorff 距离进行二值边缘图像匹配；刘坡等［10］为解决多尺度空间区域特征匹配的阈值问题，采用均方根误差（Root Mean Square Error，RMSE）度量和相邻元素的聚类算法匹配区域特征；Kumar 等［11］采用基于闵可夫斯基距离相似性度量的形状匹配，有效地提高了识别准确率。然而，此类度量函数依赖于特征描述子效率，且计算时间复杂度较高。典型的基于图像相关的相似性度量方法［12］有：Wei 等［13］提出了基于归一化互相关的快速模板匹配算法，采用相关系数法比归一化积相关法（Normalized Product correlation，NProd）抑制了噪声；Mahmood 等［14］提出了一种基本/扩展模式部分相关消除的算法；Kolar等［15］利用相位相关方法极大地削减了度量函数对图像灰度的依赖；Woo 等［16］采用互信息提高了度量函数的鲁棒性。此类方法主要用于灰度特征的匹配，因此方法简单易理解，但匹配精度不高。典型的基于纹理、颜色、直方图统计、时间序列等特征的度量方法［17］有：Rubner 等［18］提出了基于两种直方图分布之间的地球移动距离用于基于内容的图像检索；Yoon 等［19］提出的独特相似性度量方法解决了立体匹配中存在的模糊点问题；Wong等［20］通过使用图像间的结构关系改善了特征匹配的效率；Zhou 等［21］采用互信息提高了匹配效率；Guo 等［22］提出了一种计算邻域窗口图像平均结构相似性指数算法；Lin 等［23］基于“相似物体具有相似邻域”提出了一种相似性度量方法。

针对结构复杂、纹理重复严重的图像，若采用目前单一的特征匹配度量方法，特征匹配结果可能存在以下问题：1）误匹配率高且正确匹配数量少；2）匹配结果鲁棒性较差。为了提高基于图像的特征匹配的效率，本文将局部特征点描述子、特征点之间几何空间聚类约束和特征点之间图像灰度信息引入到特征匹配度量过程中，设计了一种基于加权相似性度量的特征匹配方法。该方法依据基于网格多密度聚类的特征匹配（Feature Matching based on Grid and Multi-Density Clustering，FM_GMC）算法［24］得到的对应聚类区域，首先在图像间的聚类区域采用Hausdorff 距离（Hausdorff Distance，HD）度量聚类区域之间的空间上下文相似性；其次，采用Canny 从聚类区域中获取边缘特征点并用尺度不变特征变换（Scale Invariant Feature Transform，SIFT）描述子描述聚类区域的边缘特征点，利用欧氏距离（Euclidean Distance，ED）度量聚类区域内的特征点外观局部梯度信息之间的相似性；然后，采用归一化互相关（Normalized Cross Correlation，NCC）方法度量特征点局部区域内灰度信息的相似性；最后，根据HD、ED 以及NCC 所带来的影响大小不同，分别赋予它们不同的权值，设计一种加权相似性度量函数。最终正确匹配结果采用最近邻距离比值（Nearest Neighbor Distance Ratio，NNDR）确定。

1 相关定义

给定一对图像{A，B}，图像A有p个特征点，图像B有q个特征点，分别表示为PA={XAi(x，g)，i=1，2，…，p}，PB={XBi(x，g)，i=1，2，…，q}，其中x为特征点几何位置坐标即(x，y)，g为灰度信息。SAi是任一特征点XAi的SIFT描述，记为SAi(fA1，fA2，…，fA128)。基于上述描述，HD、ED 和NCC 分别可定义为：

定义1L(PA，PB)是PA与PB之间的HD，dPB(XAi)为任一特征点XAi中几何位置与PB内所有特征点几何位置之间距离的最小值，‖ * ‖是一种距离范式如L2，h(PA，PB)是PA内所有特征点dPB(XAi)的最大值，L(PA，PB)是PA到PB的距离或者PB到PA的距离的最大值，即PA与PB之间的HD。

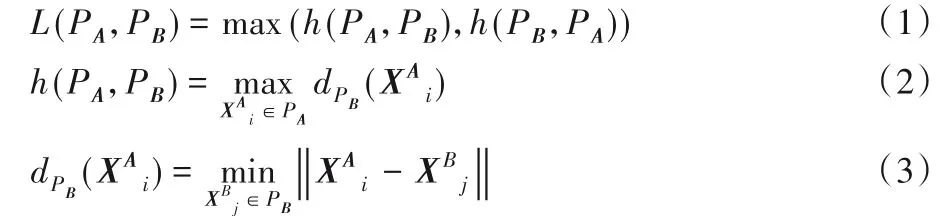
定义2特征描述子之间的欧氏距离d(SAi，SBj)为：

定义3图像A与B中像素灰度间的NCC可定义为：

其中：gA和gB分别为图像A的中心像素灰度值和匹配图像B的中心像素灰度值分别为图像A的平均灰度值和匹配图像B的平均灰度值。

2 加权相似性度量特征匹配

在基于图像的特征匹配过程中，由于采集的图像易受到光照、环境、尺度等因素影响，不同视角下的图像匹配特征点之间存在着仿射、射影等变化，直接导致图像匹配特征点之间的空间位置改变，尤其是针对结构复杂、重复纹理现象严重的图像，特征点之间的空间位置改变会导致特征点周围局部梯度信息产生变化，进而产生了较多噪声点，直接影响了图像之间的特征匹配效率。因此，在图像特征匹配过程中，若仅考虑图像特征点之间的局部梯度信息，则特征匹配结果将产生误匹配率较高、匹配鲁棒性较弱等问题。

为了提高特征匹配效率，本文针对特征匹配过程由单一的特征点局部梯度度量函数易产生特征匹配结果错误率高、匹配结果鲁棒性较弱等问题，结合FM_GMC 算法［24］，在特征聚类块的基础上提取图像边缘信息，同时融入基于距离相似性度量方法与基于图像相关的相似性度量方法，设计了一种加权相似性度量的特征匹配方法。该方法首先根据FM_GMC算法将图像划分成多个对应聚类区域，在此基础上，利用Canny 算法和SIFT 算法得到几何信息和特征点的描述信息。最后，采用加权相似性度量函数进行灰度特征、局部梯度特征以及空间几何特征的度量。具体过程如图1所示。

图1 加权相似性度量特征匹配过程Fig.1 Flowchart of feature matching based on weighted similarity measurement

2.1 特征点的描述

2.2 度量函数

给定两个对应聚类区域Ai和Bi分别包含p、q个边缘特征点及相应的特征描述信息，根据式（1）～（3）可将D1定义为Ai和Bi对应聚类区域内特征点空间位置的HD：

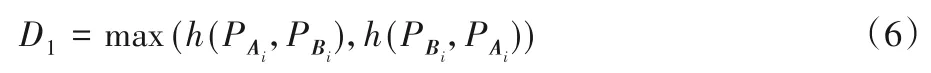
D2为特征点描述子之间的ED，其中特征点通过Canny 提取，采用SIFT 进行特征描述。用fAimj和fBinj分别表示Ai和Bi中特征点的描述子，参照式（4），Ai中特征点与Bi中第q个特征点的描述子间的欧氏相似度量D2可通过式（7）进行计算。

D3为NCC 估计图像中像素强度的相似度，以聚类区域Ai与聚类区域Bi为例，Ai(x，y)表示Ai中以(x，y)为左上角点与Bi模板一样的子块，且Bi子块大小为m，通过相关系数式（8）可得到Ai与Bi间的相关系数矩阵ρ(x，y)，并判断它们是否相关。

最后，基于D1、D2、D3和三个加权参数，图像区域(Ai，Bi)内特征点之间的度量函数D可定义为：

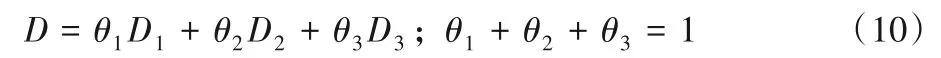
设DN和DM分别为聚类区域Ai中任一特征点与Bi中所有特征点距离之间的最近邻和次近邻值，比值Rr由式（11）确定。通过设置阈值R可剔除误匹配，如果Rr＜R，则保留该匹配。

2.3 算法描述及分析

依据上述加权相似性度量，结合文献［24］，基于FM_GMC的WSM特征匹配算法描述如下：

算法1 加权相似性度量方法。

输入 图像A和B；

步骤1 根据FM_GMC 算法的结果将图像A和B分成多个对应的聚类区域；

步骤2 采用Canny提取各聚类区域内的边缘特征点；

步骤3 采用SIFT描述子描述边缘特征点；

步骤4 计算各对应聚类区域边缘特征点间的Hausdorff距离D1；

步骤5 计算各对应聚类区域边缘特征点描述符之间的欧氏距离D2；

步骤6 计算各对应聚类区域内像素之间的NCC记为D3；

步骤7 将D1、D2和D3合并到D中，并分配不同的权重；

步骤8 在D各横向量中查找最近邻和次近邻，分别标记为DN和DM；

步骤9 设置阈值R并且计算Rr=DN/DM；

步骤10 如果Rr ＜R，保留匹配，否则删除匹配。

上述WSM 方法可有效地剔除由环境、光照、尺度等原因产生的噪声点，具体原因为：依据FM_GMC 算法［24］得到的对应聚类区域，首先在图像间的聚类区域采用Hausdorff 距离（D1）度量对应聚类区域之间的空间相似性，从而保持特征匹配区域之间的空间位置的一致性，有效地剔除由空间不一致造成的噪声点；其次，采用Canny 从聚类区域中获取边缘特征点，并用SIFT 描述子描述聚类区域的边缘特征点，利用欧氏距离（D2）度量聚类区域内的特征点局部梯度信息间的相似性，进而从图像旋转和尺度上保证对应边缘特征点的局部梯度一致性，进一步剔除由旋转和尺度变化形成的噪声点；然后，为了减小光照对图像的影响，采用了NCC 方法（D3）来度量特征点局部区域内灰度信息的相似性，有效地剔除由光照变化形成的噪声点。

2.4 算法复杂度分析

为方便计算，设图像A和B提取的SIFT 特征点个数均为N，图像A和B的网格数量为M。若采用传统的RANSAC 算法进行特征匹配，其时间复杂度为O(N2+N)。因为WSM 的特征匹配均在对应聚类区域内进行，所以时间复杂度主要取决于图像划分网格的数量M。表1给出了WSM算法各阶段时间复杂度。

表1 WSM算法各阶段时间复杂度Tab.1 Time complexity of the WSM algorithm in different stages

由于FM_GMC算法的网格数量M大于9，所以从表1中可以得出如下结论：相较于传统的随机抽样一致（RANdom SAmple Consensus，RANSAC）匹配方法，WSM 特征匹配的时间复杂度O(2*N/M+3*(N/M)2)＜O(N2+N)。因此，算法WSM在时间上优于传统的RANSAC算法。

3 实验结果与分析

本章从精确性和鲁棒性两个方面对WSM 的性能进行了评价，并将WSM 与SIFT+RANSAC、SURF（Speeded-Up Robust Features）+RANSAC、FM_GMC、LIFT（Learned Invariant Feature Transform）和EECS442（http：//web.eecs.umich.edu/～fouhey/teaching/EECS442_W19/index.html）等匹配算法进行比较。实验环境为：Windows 10 操作系统，2.3 GHz Intel Core i5 处理器，4 GB 内存；以及开放源码工具箱opencv3.2.0、matlabR2014a、python3.6.0。

3.1 参数分析

算法WSM 涉及到的关键参数分别为：θ1、θ2、θ3和R，为比较参数的不同取值对WSM 效果的影响，本文进行了如下的实验，其中参照传统SIFT特征匹配算法中的取值情况，R取0.6。根据θ1、θ2、θ3的不同取值能够发现特征匹配的精确率p（Precision）的变化浮动比较大。精确率p计算参考文献［25］，可定义为匹配结果中正确匹配对占所有匹配对的比率：

表2给出了当θ1取值为0.15、0.2、0.3、0.4、0.5 时，θ1、θ2、θ3与特征匹配精确率p之间的数据。

表2 θ1、θ2、θ3与精确率p的关系Tab.2 Relationship between p and θ1，θ2，θ3

从表2可以得到以下结果：

1）WSM 算法特征匹配精度最高时的取值为：θ1=0.4，θ2=0.35，θ3=0.25。

2）在特征匹配过程中，特征聚类区域之间的相似度可通过两个区域之间的空间位置相似度D1定义。从表2中的结果可以看出，D1对应权值θ1的改变对特征匹配结果的影响最大，这是由于WSM 的匹配效果好坏主要取决于初始匹配结果及初始聚类区域的选择，从同一对象提取出的特征点的位置信息往往保持一致。因此，对于WSM 来说，对应特征区域的精度对特征匹配结果影响最大。如在参数θ3=0.15 的条件下，θ1变化范围为0.2～0.5，匹配精度对应变化范围为0.74～0.9。

3）局部几何相似度D2主要描述了特征描述子相似度。从表2可以看出，D2对应权值θ2对匹配结果的影响次之，这是由于针对特征点而言，特征描述子的相似性能够更详尽地刻画特征局部领域之间的相似关系。如在参数θ1=0.3 的条件下，θ2变化范围为0.2～0.65，匹配精度对应变化范围为0.78～0.92。

4）NCC 度量因子D3主要描述了特征点与周围邻域间的灰度变化情况，因此，可作为补充条件有效地剔除由于光照变化造成的误匹配。从表2 中可以看出，D3对应的权值θ3对特征匹配精度影响最小。

依据表2可得出如下结论：当θ1的取值范围为0.3～0.45，θ2的取值范围0.25～0.35，θ3在0.2～0.25 时，特征匹配精度可保持在90%左右，因此本文建议θ1、θ2、θ3的取值分别为0.4、0.35、0.25。

3.2 精确率和鲁棒性验证

本节从精确率上分析了WSM 与其他算法（SIFT+RANSAC、SURF+RANSAC、LIFT、EECS442 以及FM_GMC）的比较结果。其中WSM 中各参数设置分别为：θ1=0.4，θ2=0.35，θ3=0.25，R=0.6，其他算法的参数设置均提供默认值。图2 与图3 分别展示了各匹配算法精确率与匹配数量间的关系：图2 中的横轴代表匹配算法所用的图像数量，纵轴代表各算法在当前输入图像下的平均精确率；图3 中的横轴代表各算法20 幅图像的平均正确匹配数量，纵轴代表采用的匹配算法。

图2 各算法的平均精确率Fig.2 Average precisions of different algorithms

从图2与图3中发现：

1）相 较 于 SIFT+RANSAC、SURF+RANSAC、LIFT、EECS442和FM_GMC，WSM的精确率保持在92.08%左右。

2）相 较 于SIFT+RANSAC、SURF+RANSAC、LIFT 和EECS442，FM_GMC 将聚类引入到特征匹配中，保证了特征匹配的空间一致性，提高了特征匹配的精度，但是匹配的数量比WSM 少。这是由于WSM 是通过Canny 提取边缘特征点，而FM_GMC 是通过SIFT 来提取特征点，导致其提取出的图像特征点数量较少。

3）当光照差异较大时，SIFT+RANSAC 和SURF+RANSAC的匹配效果较差且匹配数量较少；当图像发生旋转变换或尺度缩放时，EECS442的匹配效果最差，但它考虑到图像中所有的Harris角，所以在匹配的数量上做得很好。

4）LIFT 采用深度网络架构并且使用最近邻匹配策略，提高了匹配精度，但匹配数量不理想；而WSM 将空间位置、特征信息和灰度信息融合在一起，同时提高了匹配的精确率和匹配数量。

部分匹配结果如图4 所示。从匹配结果中可以看出，WSM 在图像发生尺度缩放、旋转变化等情况下，特征匹配数量较多且匹配准确率较高。

图3 各算法20幅图像的平均正确匹配数量Fig.3 Average matching numbers of different algorithms

图4 旋转、尺度缩放匹配结果Fig.4 Experimental results of feature matching with rotation and scaling

3.3 WSM算法在三维重建中的应用

依据WSM 算法得出特征匹配点应用于古建筑图像三维重建的流程为：首先，选择两幅晋祠图像用于初始化后续所需的一系列场景结构以及相机的运动计算。由于三维重建的前提需要，这两幅图像间必须有充足的匹配点，本文算法WSM提供的古建筑图像特征匹配数量平均值达到226，基本满足其要求。其次，根据两幅图像的匹配关系，可通过三角测量进行场景重建，并向已重建好的结构中添加23 幅图像。最后，由于两幅图像对应的初始相机的位姿已被确定，随着新图像的不断加入和重建计算，重建结构也随之不断地更改，新的三维点更新生成。这一部分是通过中国科学院自动化研究所提供的软件实现的。重建结果如图5，其中重建点云个数为5 762 844；图6 为Visual SFM 三维重建效果图，其重建点云个数为4 108，特征匹配结果在三维重建效果上得到验证。

图5 WSM的晋祠三维重建效果图Fig.5 3D reconstruction effect of Jinci temple by using WSM

图6 Visual SFM晋祠三维重建效果图Fig.6 3D reconstruction effect of Jinci temple using Visual SFM

4 结语

针对结构复杂、纹理重复的对象，为了提高图像的特征匹配的效率和鲁棒性，本文提出了一种基于加权相似性度量的特征匹配方法WSM。该方法首先根据FM_GMC 算法将图像分成若干对应聚类区域；其次，采用Canny 方法提取对应聚类区域内的边缘特征信息，并利用SIFT 进行几何特征描述；然后，结合聚类区域的空间一致性信息、匹配特征间的局部描述信息和特征点周围领域内灰度信息，采用加权的方法进行相似性度量；最后，采用晋祠古建筑验证了WSM 算法的有效性。由于该算法不仅从全局上考虑了匹配特征点间的空间一致性，而且从旋转、尺度、灰度方面考虑了匹配特征点间的局部结构特征，从而有效提高了特征匹配的效率。