基于基准点引导的无人机光电平台定位精度分析与研究

张帅 韩松伟 白冠冰 刘仲宇

（中国科学院长春光学精密机械与物理研究所 航空成像与测量技术研究一部 吉林省长春市 130033）

1 引言

通过无线遥控装置控制的不载人飞行器统称为无人机，因其具有造价低、体积小、使用方便、对战场适应能力强等特点得以飞速发展[1]。无人机光电平台是无人机基本的任务单元，是一种集光电探测系统、伺服控制系统、复杂数据融合系统等系统为一体的先进机载光电系统，能够对目标进行搜索、跟踪和捕获，具有实时性高，覆盖范围广等优点[2]。

复杂的战场形势要求军用无人机光电平台具有目标定位及地理位置引导功能。在进行目标定位与位置引导时，集成子惯导系统的光电平台可根据自身子惯导提供的无人机位置及姿态信息来进行位置信息或角度信息进行解算，此类光电平台在定位及引导计算过程中不会引入减震器位移带来的角度误差，定位与引导精度相对较高，但由于惯导系统的集成则会增加研发成本，同时导致光电平台体积和重量增大，增加系统的复杂度，不适用于中小型无人机[3]。不搭载子惯导的光电平台具有系统简单化、轻量化的优点，但在安装时需要与飞机之间进行复杂的标校，使光电平台的初始零位与飞机航姿角度的重合，同时在飞行中会引入飞机与光电平台之间减震器角位移带来的角度误差，定位与引导精度受飞机姿态影响较大[4]。

针对不搭载子惯导的光电平台定位精度较差的问题，本文对无人机定位误差进行了分析，提出一种基于基准点引导的无人机与光电平台的角度误差修正方法，在无子惯导的光电平台上，通过在飞行前或飞行中对地面已知位置的多个目标进行位置引导，将引导的角度误差值反馈于光电平台角度传感器的初始零值的方法，可以在飞行航姿相对稳定的一段时间内，消除由于减震器位移带来的旋转角度误差和平台基板安装时带来的安装角度误差，提升定位精度。

2 目标定位与位置引导基本方法

无子惯导的光电平台目标定位通常指通过利用光电平台搭载的激光测距机的测距值、无人机提供的姿态信息、地理坐标信息，光电平台的姿态信息，对视轴中心的目标地理位置位置进行解算[5]。位置引导则是已知目标的地理坐标，利用无人机提供的姿态信息、地理坐标信息，计算光电平台需要引导的姿态角，通过伺服控制系统使光电平台旋转到指定角度，使目标出现在视场中心[6]。

2.1 定位与引导坐标系的建立

为实现对视轴中心目标的定位和已知目标的引导，需要建立合适的辅助坐标系，将目标在视轴上的坐标转换为在大地坐标系下的坐标。通常建立视轴坐标系、平台坐标系、载机坐标系、载机地理坐标系、地球直角坐标系、大地坐标六个坐标系[7]。

（1）视轴坐标系（Xs，Ys，Zs）：原点为相机中心投影位置，Z 轴正向为视轴指向方向，当视轴垂直向下时X 轴正向为与飞机中轴线平行且指向机头的方向，Y 轴与X、Z 轴构成右手坐标系。

（2）平台坐标系[8]（Xp，Yp，Zp）：原点与视轴坐标系的原点重合，Z 轴正方向为相机视轴与飞机中轴线平行时指向机头的方向，X 轴垂直于飞机中轴线且指向飞机上方，Y 轴正向与飞机右机翼轴线平行。此时平台方位角为0，俯仰角为0。

（3）载机坐标系[9]（Xz，Yz，Zz）：原点为载机的质心位置（通常为载机惯导的安装位置），Z 轴沿着飞机中轴线方向，指向飞机正前方。Y 轴沿着机翼方向，从飞机后面往前看，Y 轴指向飞机右侧，X 轴垂直于ZOY 平面，并与Y 轴和Z 轴构成右手坐标系。

（4）载机地理坐标系[10]（Xd，Yd，Zd）：原点与载机坐标系重合，Z 轴指向正北，X 轴沿大地高方向指向天顶，Y 轴与ZOX 面垂直，并与X 轴和Z 轴构成右手坐标系。

（5）地球直角坐标系[11]（Xq，Yq，Zq）：原点位于地球质心，Z 轴指向地球北极，X 轴指向格林尼治子午面与地球赤道的交点，Y 轴垂直于XOZ 平面构成右手坐标系。

（6）大地坐标系[12]（L，A，H）：与地球直角坐标系完全重合，以国际地球参考系统WGS-84 为基准建立，以经度、纬度、高度代表地球上任一地点的位置。

2.2 定位坐标系的转换

目标定位的坐标系转换过程如图1所示，即已知目标在视轴坐标系下的位置和平台坐标系下的位置，通过载机坐标系、载机地理坐标系、地球直角坐标系的坐标转换，得到目标在大地坐标系下的位置[13]。

图1：目标定位坐标转换过程

当地面操作人员通过光电平台发现感兴趣目标时，操纵光电平台使目标出现在视场中心，并对目标进行激光测距，得到目标相对于光电平台的相对距离R，此时光电平台的方位角、俯仰角分别为C、B，无人机的航向角、俯仰角、横滚角分别为F、T、P，无人机的经度、纬度、高度分别为L0、A0、H0，此时目标在光电平台视轴坐标系下的坐标为：

将目标从视轴坐标系向平台坐标系转换，绕Y 轴旋转俯仰角B，绕X 轴旋转方位角C，旋转矩阵为：

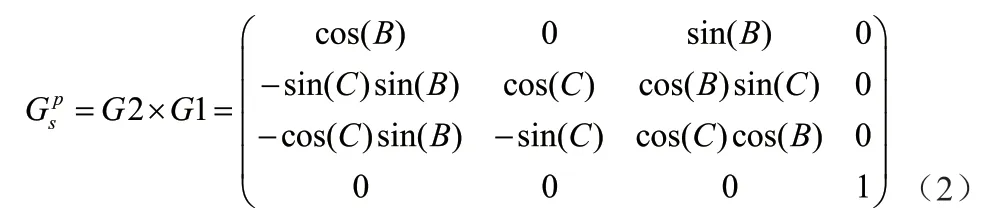
其中：

光电平台安装到无人机上时，会存在一定的安装偏角：方位安装偏角f、俯仰安装偏角t、横滚安装偏角p；通常该安装偏角会在光电平台安装到无人机上时，通过一系列复杂的光学标校得到。将目标从平台坐标系向载机坐标系转换，绕Z 轴旋转横滚安装偏角p，绕Y轴旋转俯仰安装偏角，绕X轴旋转方位安装偏角f，旋转矩阵为：

将目标由载机坐标系向载机地理坐标系下转换，需要根据飞机当前的航向角、俯仰角和横滚角进行坐标旋转变换，在载机坐标系下，绕Z 轴旋转无人机横滚角P，绕Y 轴旋转无人机俯仰角T，绕X 轴旋转航向角F，旋转矩阵为：

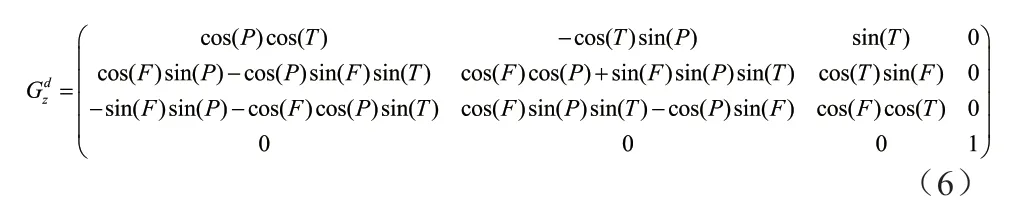
将目标从载机地理坐标系向地球直角坐标系下转换，需要根据当前飞机的经度A0、纬度L0、高度H0，进行地理坐标系的的旋转与平移。旋转矩阵为：

其中：

N 为载机的卯酉圈曲率半径：

a 为地球长半轴，e 为椭球第一偏心率平方。

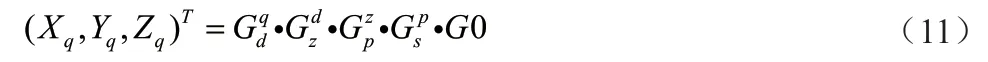
其中：

2.3 位置引导坐标系转换

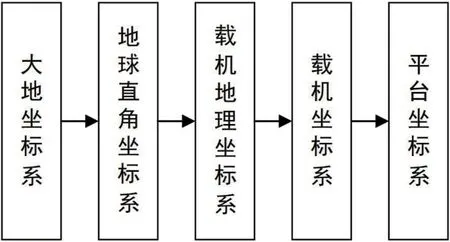
图2：位置引导目标转换过程

由公式可计算得出目标在第地球直角坐标系下的坐标(Xq,Yq,Zq,1)T：

针对轮滑技术学习的这些特点，以学生为主体，精讲多练，将个别教学，友伴群体教学、轮滑社团三种教学组织形式贯穿始终，衔接课堂学习与课后学习。各教学组织形式相辅相成，互为基础，促成了学生对轮滑技术的掌握，并强化学生运动锻炼的习惯

由目标位置由地球直角坐标系向载机地理坐标系转换，转换矩阵为：

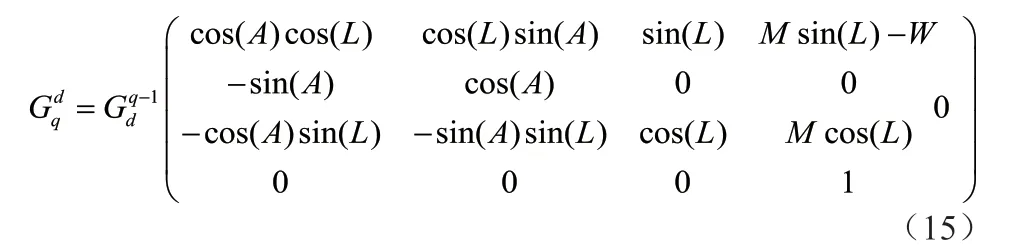
同理，目标位置由载机地理坐标系向载机坐标系转换，旋转矩阵为：

目标位置由载机坐标系向平台坐标系转换，可得目标在平台坐标系下的坐标旋转矩阵为：

由公式（18），可以计算出目标在光电平台下的方位角与俯仰角。

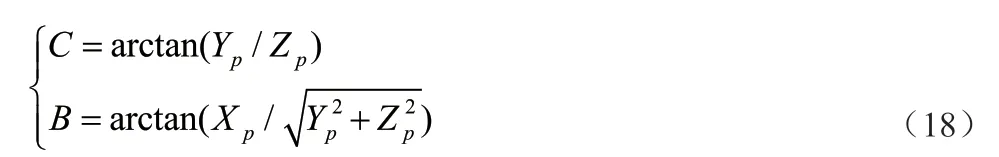
2.4 目标定位与位置引导的关系

由上述分析可知，在目标定位与位置引导算法实际运行过程中，必要的已知量均为无人机的航向角、俯仰角、横滚角、经度、纬度、高度、无人机与光电平台的方位安装偏角、俯仰安装偏角、横滚安装偏角；目标定位为根据光电平台的方位角、俯仰角、激光测距值解算视轴中心目标的地理坐标；位置引导为已知目标的地理坐标，解算光电平台需要引导的角度。实际上，目标定位与位置引导的过程互为逆过程。

3 目标定位精度分析

通常，无人机光电平台目标定位为精度主要由算法输入变量的精度决定，主要的误差来源于光电平台的角度误差、光电平台激光测距机测距值误差、无人机姿态角误差、无人机地理位置误差、无人机与光电平台安装偏角测量误差；采用蒙特卡洛法对目标定位误差进行分析，定位误差数学模型可以表示为：

其中ΔL、ΔA、ΔH 为定位结果的误差，Qi为定位算法中平台方位角C、平台俯仰角B、无人机方位角F、无人机俯仰角T、无人机横滚角P、无人机经度A0、无人机纬度L0、无人机高度H0、方位安装偏角f、俯仰安装偏角t，横滚安装偏角p 等参数的的给定值，ΔQi为对应参数值的误差。

给定初始参数，如表1所示，同时给定服从正态分布的初始参数误差均方根，如表2所示。

表1：目标定位初始参数值

表2：目标定位初始参数误差均方根

根据上述初始值建立1000 个随机变量的样本模型，目标定位误差图如图3所示。

图3：目标定位误差分布图

图4：目标定位平面定位误差分布直方图

通过在光电平台与无人机的安装基板上安装减震器的方法，可以有效地减小无人机振动对光电平台成像质量的影响，安装示意图如图5所示；但由于无人机姿态角的变化、无人机机体的高频振动、光电平台重心的变化和风阻的影响，会使减震器每个方向上的形变不一致，造成光电平台与无人机之间存在一定的角位移，如图6所示。通过在五轴飞行模拟摇摆台上进行试验，由于飞行姿态所引起的减震器角位移最大可达1°，此量级的误差会在目标定位解算过程中产生不可忽视的影响。国内关于目标定位精度研究工作中，部分研究没有考虑减震器角位移引起的角度误差；部分研究提出通过在光电平台内部安装平台内部惯导的方式，用平台惯导代替无人机惯导来消除减震器角位移误差，但由于无人机光电平台内部空间有限，安装平台惯导势必会压缩光电平台的成像空间，造成光学指标下降，同时平台内部惯导受限于光电平台体积，输出的位置信息和姿态信息精度会明显下降，同样会造成较大误差[14]。

图5：光电平台安装图

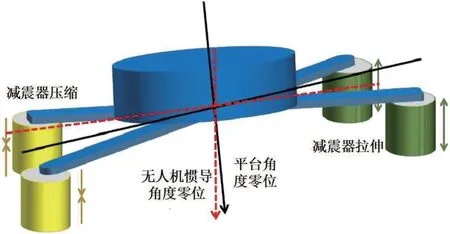
图6：光电平台减震器角位移示意图

在定位解算过程中增加安装基板坐标系，如图7所示，模拟由于飞机姿态变化引起的减震器角位移误差。在飞机航姿相对固定的一段时间内，以表3 的误差值作为光电平台与无人机之间的角位移误差均方根，即安装基板坐标系与载机坐标系之间的旋转角，以表1 和表2 的给定值作为定位解算的初始值与初始参数的误差均方根，建立1000 个随机变量的样本模型，考虑减震器角位移后，目标定位误差如图8所示。

图7：增加安装基板坐标系后的目标定位坐标转换过程

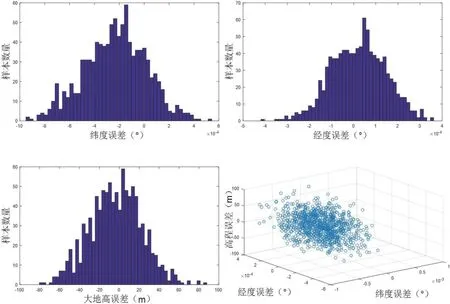
图8：减震器角位移影响后的目标定位误差分布图

表3：减震器角位移误差均方根值

将仿真结果取均方根值，光电平台的纬度误差均方根为3.5193×10-4°，经度误差均方根值为1.23196×10-4°，高度误差为26.8295。平面定位误差如图9所示，平面定位误差均方值为40.2899m。由上述分析可知，当减震器引起的角位移误差如表3 时，平面定位误差将增大33.5%。

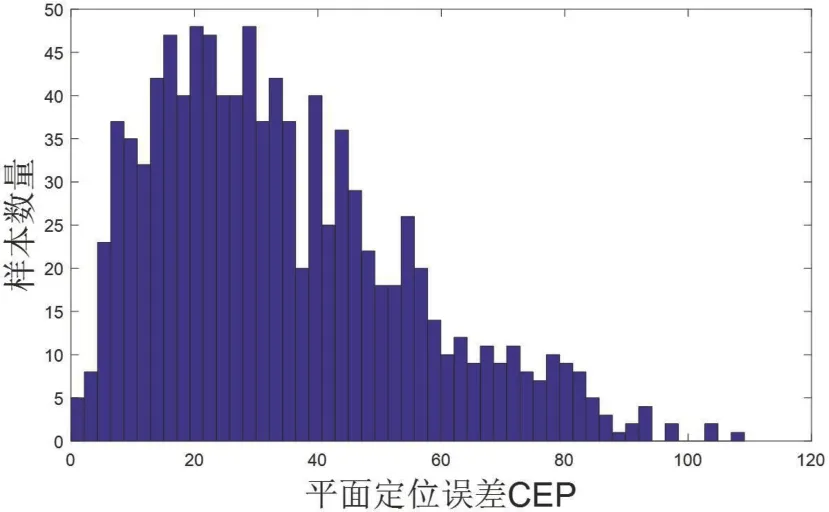
图9：减震器角位移影响后的目标定位平面定位误差分布直方图

4 基于基准点引导的光电平台定位精度提升方法

在飞机航姿相对固定的一段时间内，由减震器引起的角位移基本上是固定的，但是此角位移产生的误差在无人机飞行时是不可测量的，如此时开启对目标的定位，那么根据上节所述定位误结果的平面误差将会大幅增大，造成定位结果不准确。

目标定位与位置引导的过程互逆，如图1 与图2所示，目标定位解算过程中存在的初始值误差、减震器角位移误差，在位置引导解算过程中同样存在，目标定位误差体现在与实际目标地理位置的位置偏差，位置引导误差主要体现在光电平台光轴指向角度值与实际光轴指向目标角度值的偏差，如能将位置引导结果的角度误差进行修正，则可以消除目标定位过程中所有的固定角度初始值误差，包括方位安装偏角、俯仰安装偏角、横滚安装偏角、航姿固定时间内的减震器位移角，提高目标定位精度，同时可以省去光电平台安装到无人机上的复杂光机校靶过程。

基于基准点引导的无人机光电平台定位误差补偿方法原理如图10所示。在无人机航姿相对固定的一段时间内，对地面多个已知位置坐标的目标点进行位置引导，通过操控旋转光电平台直至目标出现在图像视场中心的方式测出旋转前后的方位角与俯仰角的差值，将引导的多个基准点的方位角与俯仰角的差值Δφi取均方根，通过“校靶”功能，将位置引导的误差角均方根值迭代到光电平台的方位角与俯仰角上，对光电平台的方位角与俯仰角初始值进行修正，可以基本消除在此航姿下由于安装偏角与减震器角位移误差带来的光电平台定位误差。

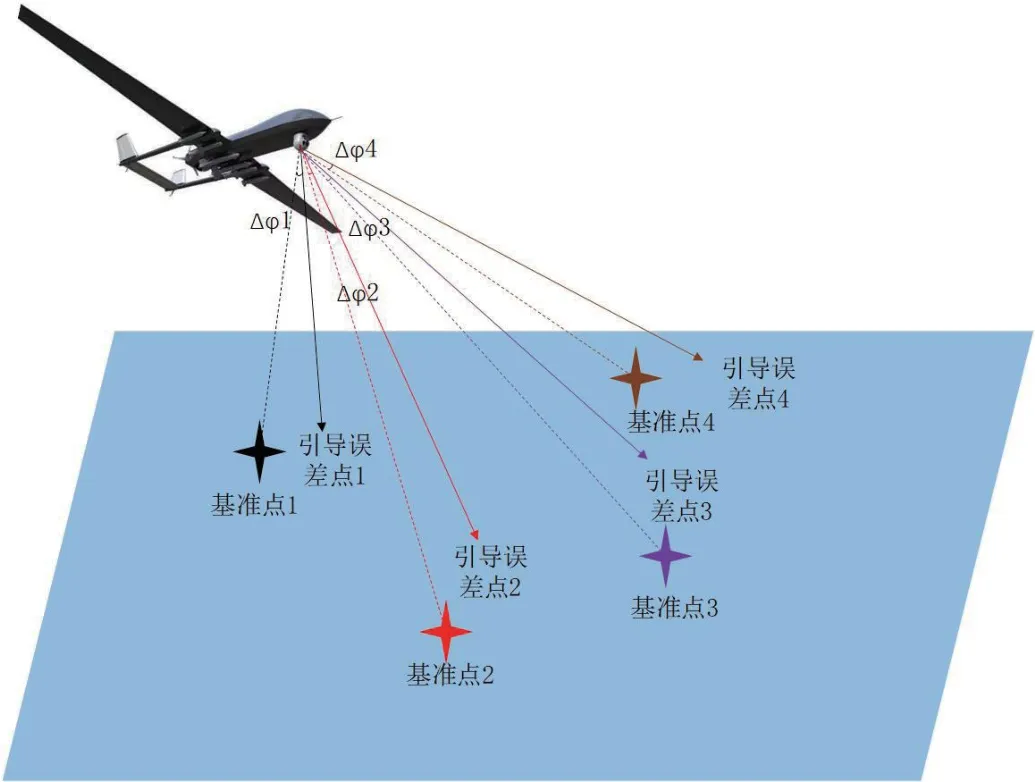
图10：基于基准点引导的定位误差补偿方法原理图

采用蒙特卡洛法进行仿真，对比采用引导误差修正方法修正安装偏角和减震器角位移与不采用引导误差修正方法修正安装偏角与减震器角位移的定位结果，输入参数初始值如表4所示，初始参数误差均方根如表2所示，进行1000 次仿真试验，平面定位误差对比结果如图11所示，图11(a)为采用此方法后的平面定位误差样本分布图，图11(b)为未采用此方法的平面定位误差样本分布图。

表4：目标定位初始参数值

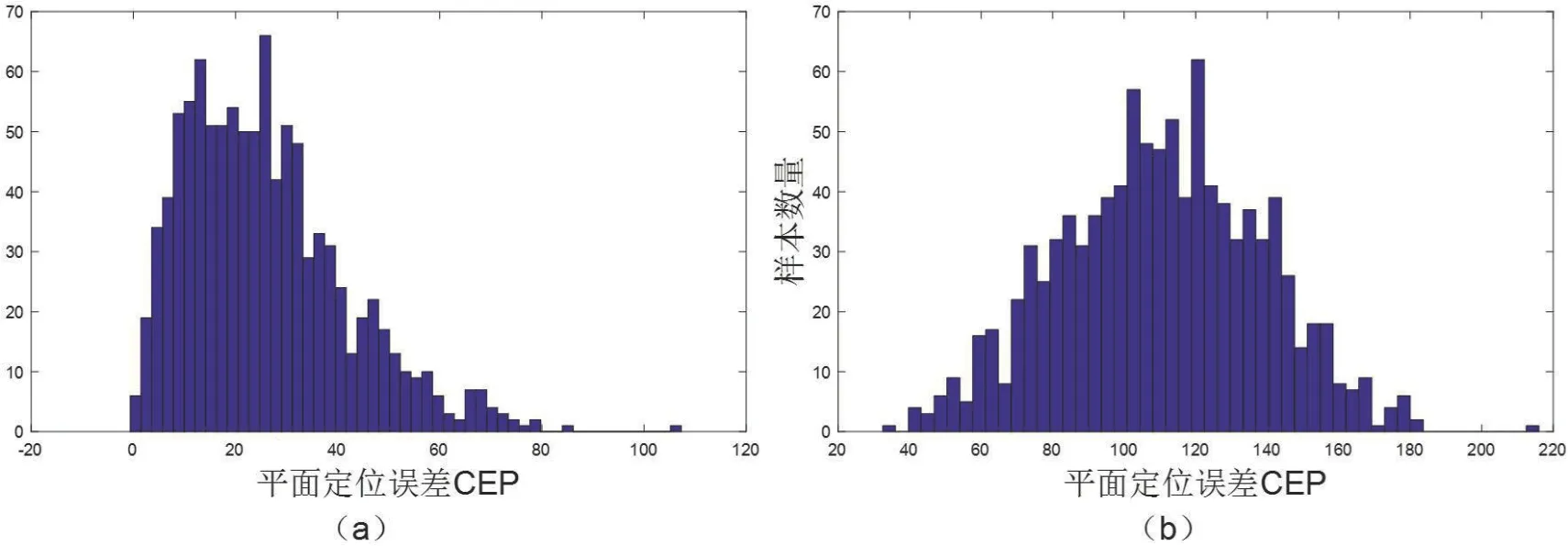
图11：平面定位误差对比结果图

根据仿真结果可知，采用基于基准点引导的光电平台定位精度提升方法补偿减震器角位移误差与安装偏角误差后平面定位误差为30.1929m，未采用次误差补偿方法的平面定位误差为111.2476m。在距离目标30km 的情况下，平面定位误差提升了80.46m，定位精度得到了较大的提高。

5 结论

本文对无人机光电平台目标定位与位置引导算法进行推导，在实际工程背景下，对目标定位过程中的定位误差进行分析，以定位算法为核心通过蒙特卡洛方法仿真验证了减震器角位移误差对目标定位精度具有较大影响，并基于此提出基于基准点引导的无人机光电平台定位精度提升方法，通过此方法可以校正无人机光电平台的安装偏角，省去了地面复杂的人工校靶过程，并可以在航姿相对固定的飞行状态下削弱由于减震器角位移带来的角位移误差，通过蒙特卡洛方法进行对比仿真试验，对距离目标30km 的目标进行定位时，平面定位误差可提升80.46m，提升了一定的定位精度。