基于高速公路收费数据的车辆分类研究
——以重庆市为例
2021-03-06马新露雷小诗马筱栎
马新露,雷小诗,马筱栎,樊 博
(重庆交通大学交通运输学院,重庆 400074)
0 引言
近年来,随着我国汽车保有量的不断攀升,高速公路交通拥堵时常发生、“非法营运”屡禁不止。高速公路出行效率下降使管理人员必须应用更有针对性的、精细化的交通管控方法[1],提升交通管控效率及服务水平,以满足车辆正常出行需求。出行群体分类是基于出行者出行相似性和规律性,提取特征将出行者划分为不同类别的方法,分类结果能为交通精细化管理及服务水平提升提供依据。
随着交通大数据获取设施不断完备以及大数据技术的快速发展,研究人员可基于交通大数据进行出行群体分类辨识模型研究,以解决传统群体分类方法样本量少、结论不准确等问题[2]。国内外部分研究人员基于自动售检票(Automatic Fare Collection,AFC)数据对出行个体进行分类研究。如刘家玮[3]利用AFC 数据,从出行强度、时间维度、空间维度及卡类型4 方面构建指标,运用两步聚类法将乘客分为4 类,基于分类结果测算优惠票价对每类乘客的转移效果;席洋[4]利用AFC 数据提取出行时间及空间特征,引入基于语义分析的主题模型,识别出10个出行主题,并在此基础上利用K均值(K-means)聚类算法将乘客分为6类;Kieu 等[5]利用AFC 数据,以出行起讫点和出发时间为指标,应用具有噪声的基于密度的聚类(Density-Based Spatial Clustering of Ap⁃plications with Noise,DBSCAN)算法将乘客分为通勤乘客、出行起讫点稳定型等4 类;Briand 等[6]通过分析法国城市雷恩2014年4月的公共交通刷卡数据,提出了一种主题模型结合高斯混合模型的方法,将乘客按照出行时间及出行模式聚类,并从智能卡的类型分析聚类成分,证明了聚类结果与出行者社会经济属性的关联性。另外,有研究者基于高铁客票数据进行铁路旅客分类研究,如吕红霞等[7]采集旅客出行数据,用凝聚法合并相关性较强的特征变量,并用近邻传播算法对旅客进行样本聚类,将旅客分为6 类。同时,也有研究者以出行车辆为研究对象进行出行群体分类研究,如畅玉皎等[8]基于上海快速路牌照识别系统采集的数据,通过K-means 聚类进行数据挖掘,提取路网中具有通勤特征的车辆,并分析了通勤车辆在路网中的出行时空分布。
已有出行群体分类研究多以城市内部出行大数据为基础,以在城市内部出行的人群为研究对象。而高速公路联网收费数据作为典型的交通大数据,记录了车辆经过高速公路收费站的详细信息,如进出口收费站点编号、车辆进出收费站时间、车型、车牌等数据,是研究高速公路出行的良好数据源。部分学者基于高速公路联网收费数据进行了研究,但集中于旅行时间预测、交通流特征分析、短时流量预测等[9-11],仅有少量学者基于收费数据进行高速公路出行群体的识别,如钱超等[12]利用ETC 收费数据提取客户细分指标,基于大型应用中的聚类(Clustering Large Applica⁃tions,CLARA)算法实现ETC 客户的聚类分析,并采用分类与回归树(Classification and Regres⁃sion Tree,CART)算法提取ETC 客户细分规则,最终将ETC 客户细分为5 类;魏广奇等[13]基于高速公路收费数据,利用聚类方法只进行通勤车辆识别,并分析通勤车辆的出行时空分布特征。
因此本文针对高速公路车辆群体分类研究较少且多只进行部分类别辨识的情况,基于高速公路收费数据,分析车辆出行特征并建立车辆出行指标,利用K-means++无监督学习算法,对高速公路出行车辆进行群体分类辨识,将具有相似出行特征的车辆划分到同一类别,并分析各类别的差异,以期为交管人员进行精细化的、更有针对性的高速公路交通管控提供依据。
1 数据准备及车辆分类流程
1.1 数据准备
本文数据来源于重庆市某高速公路特定通道2018年7月2日—2018年7月29日小型客车(7座及以下)收费数据,数据表设计见表1。2018年7月2 日—2018 年7 月29 日包含4 个完整周,其中工作日20d、周末8d。特定通道共包含5 个互通和8 个收费站,左起南环互通,属主城巴南区管辖,右至双河口互通,属南川区管辖,全长约92.4km。为方便研究,将南环互通至双河口互通方向定义为“出城方向”,反之为“进城方向”。
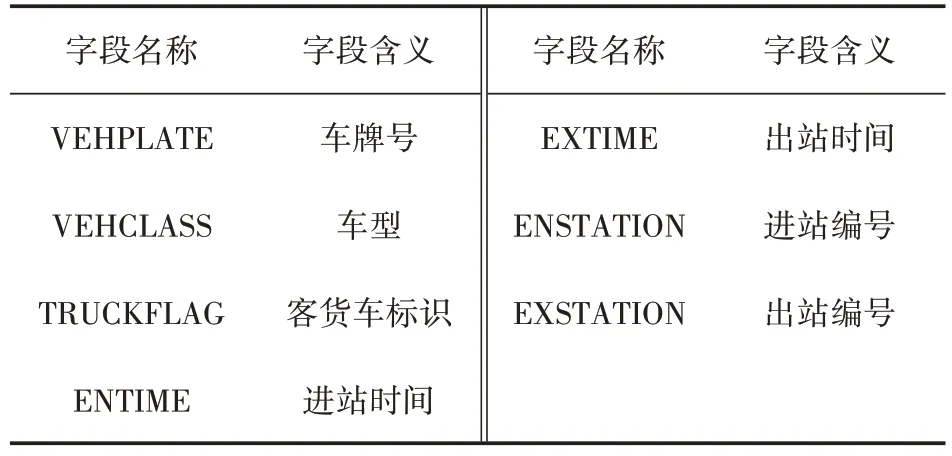
表1 高速公路收费数据主要字段
由于设备问题或人工操作失误等原因,收费数据可能包含个别错误数据。为提高研究精度,降低错误干扰,将存在缺失字段、车牌号错误、进站时间晚于出站时间、进出站时间差大于24h等情况的错误数据删除,最终保留有效数据134.6万条,对应小型客车43.6万辆。
1.2 车辆分类流程
基于收费数据,统计每周“进出城方向”各小时交通量变化情况,结果显示:周五下午、周六及周日上午出城方向车流量大,而周六及周日下午进城方向车流量较大。经分析认为,周末出城走亲访友的车辆增多,且受该地存在景区的影响,7 月后两周的周末有大量游客前往通道附近景区游玩避暑。另外,统计车辆出行次数后发现:出行1 次的车辆占车辆总数的30.95%,无法对该部分车辆进行个体出行规律分析。
若直接进行聚类,出行总次数较少而占比较大的车辆会降低分类精确度。为提高车辆分类准确性,本文采取“先定义后聚类”的方式,具体分类流程(见图1)为:
(1)清洗原始数据;
(2)将出行1 次的车辆定义为“单次出行车辆群体”;
(3)出游或走亲访友车辆群体主要在周末出行而工作日基本无出行,因此筛选出周末有出行但工作日出行为零的车辆,定义为“出游或走亲访友车辆群体”;
(4)对剩余车辆构建时空出行指标,并将指标作为聚类算法的输入,将剩余车辆分类。
2 出行车辆群体辨识准备
2.1 K-means++算法简介
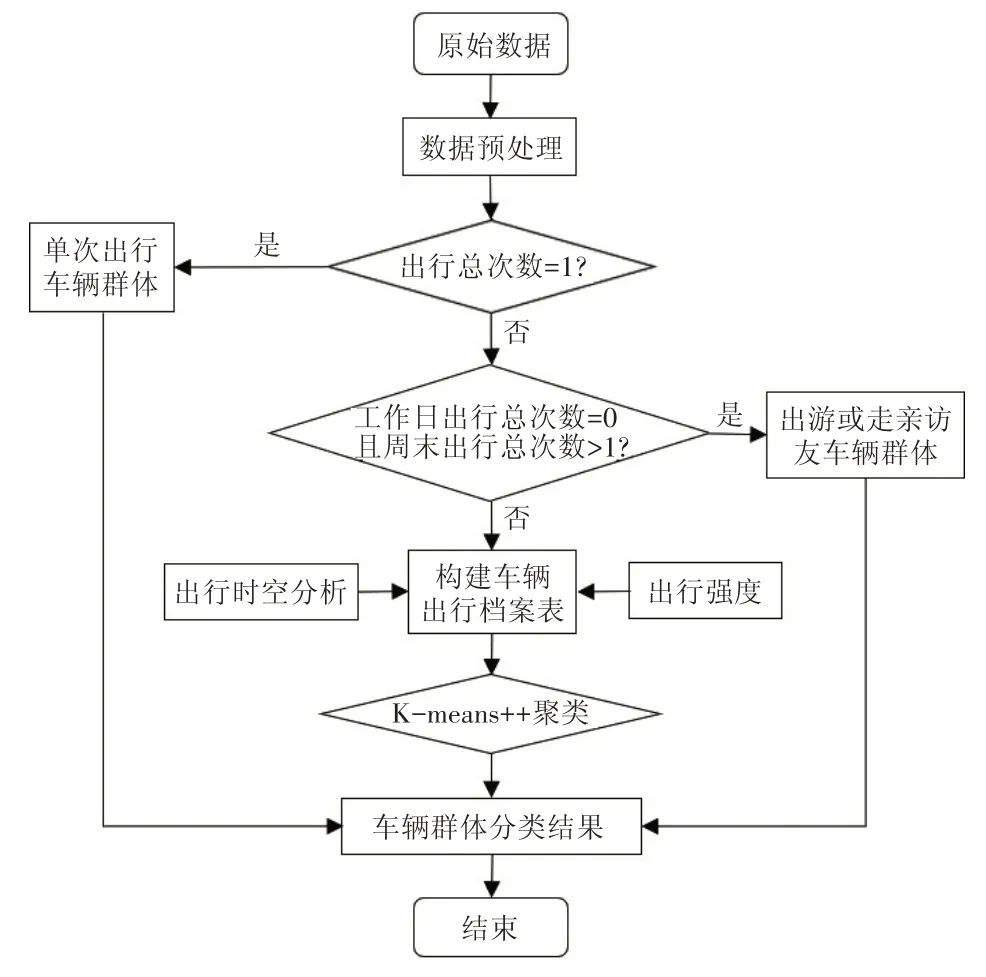
图1 车辆分类流程
K-means 作为经典的划分聚类算法,通过计算各数据点与质心间的欧式距离,将其划分到最近的质心所在的簇,从而将数据点分为具有相似特征的k个簇。K-means 具有计算简单、处理大数据效率较高和伸缩性较强等特点,因此广泛应用于各个领域。但因其k个初始质心是随机抓取的,算法对初始质心的选择异常敏感。2007 年,Arthur 等[14]在K-means 的基础上提出了Kmeans++聚类算法,该算法对初始质心的选择进行了优化,使得各初始质心分布尽可能远,以消除K-means 因生成较近的初始质心而产生的局部最优解。本文将应用K-means++聚类算法对车辆时空出行指标进行聚类,将车辆划分到不同类别。K-means++算法步骤如下:
(1)选取数据集X中任一点作为第1 个聚类中心点c1。
(2)首先计算数据点x与已有聚类中心之间的最短距离dx,然后计算其他数据点被选为下一个聚类中心点的概率px[14],最后按照轮盘法选择下一个聚类中心,即:

式(1)~式(2)中:x为数据集X中的数据点;c为聚类中心点集C中的中心点。
(3)重复步骤(2),直至选出所需的k个聚类中心点。
(4)选出k个所需的聚类中心点后,逐一计算数据集中每一个x与k个中心点的距离d(x),并将其划分至距离最小的聚类中心。
(5)针对每个聚类中心,重新计算质心作为新的聚类中心。
(6)重复步骤(4)和步骤(5),直至聚类中心不再变化或迭代次数达到预设值为止。
K-means++聚类算法需先确定最优的聚类数k,使聚类产生高的簇内相似度及低的簇间相似度。本文将分别在不同k值下计算两个内部质量评价指标:Calinski-Harabasz(CH)指标及Da⁃vies-Bouldin(DB)指标,以保证选择最优的k值。
2.2 车辆出行指标构建
将出行特征较明显的车辆划分到相应群体后,对剩余车辆的出行时空分布进行量化,作为K-means++聚类算法输入。由于高速公路出行车辆中,通勤车辆及营运车辆具有明显的时空稳定性,出行强度、时间维度及空间维度特征能较好地描述车辆出行分布规律[15]。但因生产生活需要,高速公路出行车辆在工作日的出行较稳定,而周末较分散。因此本文在“工作日”下,结合车辆出行数据,改进RFM(最近一次交易(Recency),交易频率(Frequency),交易金额(Monetary))指标体系,分别从出行强度、时间维度及空间维度3 方面构建出行指标(见表2),以满足表征不同类型车辆出行特征的基本原则,而“周末”的出行特征仅用于群体分类结果的进一步验证。

表2 车辆分类指标汇总
(1)出行强度
出行强度表征车辆出行的整体情况,包括工作日出行强度、工作日平均出行天数及其方差3个指标。工作日出行强度是工作日出行总次数与工作日出行总天数的比值,代表着车辆日均出行的频繁程度,如营运车辆工作日出行强度明显高于通勤群体车辆。工作日平均出行天数及其方差则表征车辆在工作日出行天数的分布情况及稳定性。
(2)时间维度
高速公路通勤车辆受限于工作时间要求,在时间维度上与城市通勤人群存在相似的早晚高峰出行特征,但高速公路通勤车辆晚高峰时段出行更为分散[13]。因此,本文统计车辆在工作日首次出行时间属于早高峰时段(07:00—10:00)的周均天数和车辆在工作日午平峰(10:00—15:00)出行的周均天数两个指标,作为车辆的时间维度出行指标。
(3)空间维度
出行OD 表征车辆在高速公路出行的空间分布,不同车辆群体的出行OD 稳定性存在差异,如通勤车辆的往返OD 对较其他车辆更为固定。本文分别统计车辆进城及出城方向OD 最大出行次数,并计算其与该车辆工作日出行总次数的比值,设定为工作日最大进出城OD 出行占比指标,描述车辆出行OD的稳定性。
3 聚类结果与分析
3.1 聚类结果
基于重庆某高速公路特定通道2018 年7 月收费数据,提取“单次出行”及“出游或走亲访友”的车辆,剩余24.1 万辆车。计算剩余车辆的7 个出行指标并进行聚类。为提高聚类准确性,避免各指标数量级不同对聚类结果造成影响,首先利用Z 分数(Z-score)算法将指标标准化;然后根据CH 指标及DB 指标的计算结果,确定k为6 时获得最优聚类效果;最后将7 个指标放入Kmeans++聚类算法模型中,并将聚类k值设为6,获取最终聚类结果(见表3)。
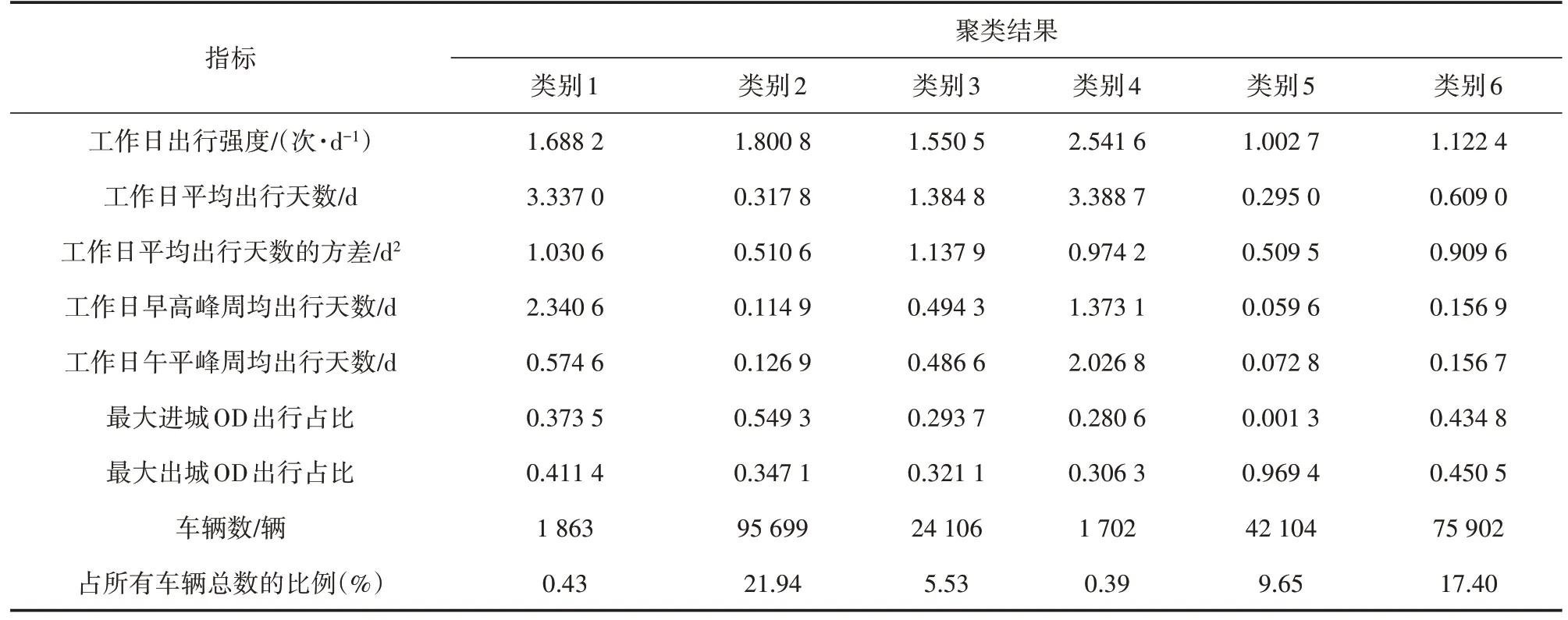
表3 K-means++聚类结果
3.2 车辆群体定义
基于聚类结果,结合已定义的“单次出行”及“出游或走亲访友”两类车辆群体,分析不同车辆类别的指标分布情况(见图2~图4),并结合实际对各类群体进行定义。
(1)类别1 出行特征明显。周均出行天数多(3.34d),拥有稳定的出行OD 对,出行强度较小(1.69 次/d),小时交通量呈明显的早晚高峰分布(见图3)。结合实际将类别1定义为“通勤车辆群体”,其在所有出行车辆中占比为0.43%。
(2)类别4 与类别1 有相似的周均出行天数,日均出行次数更多(2.54 次/d),但出行OD 对较分散,小时交通量在7:00—17:00 间无峰值,所以定义类别4为“营运车辆群体”,其在所有出行车辆中占比为0.39%。

图2 出行总次数对应车辆数占比

图3 类别1、类别3、类别4的小时交通量对比

图4 其余4类别的小时交通量对比
(3)类别3 的出行强度与类别1 相似,但周均出行天数较少,出行OD 较分散。车辆出行总次数较少,但每周工作日均有出行,该类别车辆出行规律与远距离出行进行商务洽谈的人群(如因工作需要频繁出差的人群)出行规律相似,因此将其定义为“商务车辆群体”,在所有出行车辆中占比为5.53%。
(4)类别2 及类别6 的指标中心点差距较小,虽然出行天数及出行强度分布存在一定区别,但两类别90%以上的车辆在统计周期(4 周)内出行总次数均小于6 次,小时交通量分布也基本重合(见图4)。因此,将类别2 及类别6 合并为同一类别,并定义为“零星出行车辆群体”,其在所有出行车辆中占比为39.34%。
(5)类别5 的周均出行天数及出行强度是所有类别中最小的,其最大进出城OD 出行占比呈两极分化,表明该类别车辆大多在工作日仅出行一次且为出城出行。类别5 小时交通量呈现出工作日交通量极小,但周五下午及周六、周日突增的变化趋势(见图4)。该类别车辆出行特征与“出游或走亲访友车辆”的特征类似,因此将两类别合并,共同定义为“出游或走亲访友车辆群体”,其在所有出行车辆中占比为23.37%。
4 分类结果分析及应用
本文最终将车辆划分为6 类,并分别定义为“单次出行”“通勤”“营运”“商务”“零星出行”及“出游或走亲访友”车辆群体。进一步分析各类别的出行特征,高速公路交管人员可基于此针对不同类别车辆进行精细化管理。
(1)高速公路存在具有出行强度高、特定线路出行占比大等特征的“非法营运车辆”[16],这会严重危害路网行车安全。因此交管人员可基于本文提出的方法对历史出行车辆进行“营运车辆”识别,针对识别出的“营运车辆”,重点检查其是否具备营运资格,可为打击高速公路“非法营运”活动提供依据,提高管控效率。
(2)进一步分析“通勤车辆群体”的出行OD,发现车辆多集中在“南川收费站—大观收费站”“南彭收费站—G65巴南收费站”及“南川收费站—水江收费站”等距离小于20km 的OD 对上出行。因此可考虑在“通勤车辆”出行较多的OD 对间增加早晚班车,而其余时段和路段适当缩减班车车次,这样既能缓解早晚高峰道路拥堵又能减少资源浪费。
(3)88.12%的“出游或走亲访友”车辆为渝籍车辆,可知该特定通道内景区多吸引重庆主城区人群游玩,景区可加大宣传,提高对外地出游人群的吸引力,还可为出游车辆制定更为详细的自驾游出行计划及产品推送,提升车辆“复出游”率。细化分析该类别车辆出行时空偏好发现,78.45%的车辆在以“G65 巴南收费站”为起点,景区附近收费站为终点的OD 对上出行,且多集中在周五的14:00—19:00 及周六、周日早晚高峰时段。基于此,交管部门可在景区到达车辆过饱和时段对该类车辆进行特定消息推送,引导车辆改变出游计划,达到缓解周五下午及周六、周日交通拥堵的目的。
5 结语
本文应用“先定义,后聚类”的方法,建立了一套较完整的高速公路小客车分类模型。首先定义了“单次出行”及“出游或走亲访友”出行群体,然后从出行强度、时间维度及空间维度3方面构建指标,利用K-means++算法进行聚类,最后结合实际将出行车辆划分为最佳的6类群体,分别为“单次出行”“通勤”“营运”“商务”“零星出行”及“出游或走亲访友”车辆群体。基于分类结果,交管部门可进行“非法营运”车辆识别、班车频次优化、特定消息推送引导车辆错峰出行等工作,以提升高速公路管控效率和精细化服务水平。
本文只基于出行车辆群体分类辨识结果对各类别出行特征进行描述,未来可进一步研究车辆群体出行与高速公路各站点间流量分布的关联性,并探析多类型客流分配。
