基于GWR模型的共享单车空间分布影响因素分析

杨逍遥，王建军，李国栋，程小丹

（1.长安大学运输工程学院，陕西西安 710061；2.陕西市政建筑设计研究院有限公司，陕西西安 710021）

0 引言

近年来，随着国家大力提倡绿色出行，越来越多的市民选择共享单车作为出行“最后一公里”的交通接驳工具或短途代步工具。共享单车受到用户青睐的同时也面临如何合理投放、管理及配置基础设施等问题。共享单车借、还车行为在空间上的分布差异不仅受出行者个人属性的影响，还在很大程度上受骑行环境、停放环境、车辆管理状况等的影响。厘清各影响因素对单车分布的作用机理，深入了解单车出行特征及时空分布规律，可为共享单车的投放、调度、运营管理及骑行环境的改善提供解决思路。

国内外学者对自行车及共享单车出行分布特征及其影响因素进行了大量研究。在自行车出行分布特征研究方面，出行的时间分布特征主要表现为时间的波动性，相关研究有：Vogel 等提出一种基于每个用户的单车使用强度与规律的聚类方法，研究发现周末出行人数较工作日少，且周末出行客流曲线较为平缓，无明显的客流高峰现象[1]；莫海彤等以广州市为例发现共享单车在工作日具有明显的早晚高峰，休息日的出行高峰为午间及傍晚[2]；郭海富等根据共享单车使用时间分布提出静态与动态结合的调度方式[3]。在共享单车出行的空间分布特征方面，周荣等运用数理统计法研究了共享单车空间分布，发现企业更愿意将共享单车投放在商业发达区域[4]；魏宗财等研究发现工作日共享单车出行集中于交通枢纽及教育科研功能区，休息日主要分布于商圈[5]；陈奇放等基于GIS空间分析法对共享单车骑行OD路线进行分析，发现随着距离的增加，集聚现象呈减弱趋势[6]；杨蒙等将不同的功能用地空间按共享单车分布密度进行分类，分析了分布特征与用地之间的内在机理[7]。为更好地解释共享单车出行的空间异质性，了解共享单车出行对周围空间变化的敏感性，Contardo 等为实现单车的重新分配提出了基于Dantzig-Wolfe 分解算法和Benders分解算法的调度优化模型[8]。而国内研究大多从共享单车的骑行数据出发来研究单车出行的分布特征[2,9]，较少考虑外在因素对单车出行的影响差异，鲜有研究量化分析外在环境因素与共享单车出行分布特征间的非稳定性作用规律。

在对自行车出行分布特征影响因素的研究中，国外学者在数据提取、因素考量、模型创新等方面进行了很多尝试[10-15]。Corcoran 等利用空间分析技术结合模型回归与度量方法对澳大利亚布里斯班的城市自行车系统数据进行分析，以探索周末、节假日等特殊时段及天气因素对公共自行车出行时空分布特征的影响，分析发现强风和降雨明显减少了自行车出行次数[16]。国内方面，曾小利等通过建立主要的骑行起点和终点热力图，发现短距离出行受城市主干路的影响较大，跨区域出行共享单车数量受土地利用和土地利用混合度影响较大[17]；李煜茜等从宏观、中观、微观3 个层面对共享单车骑行影响因素进行研究，发现道路环境、立体环境和道路功能是影响骑行适宜性的3 大主要因素[18]；高枫等通过引入地理探测器发现服务类设施对共享单车的影响最为显著，其次是交通可达性、自然环境类别[19]。已有研究大多基于核密度[17]、普通最小二乘法（Ordinary Least Squares,OLS）[16,18]进行回归分析判别各种因素对于共享单车出行分布的影响，假设全局参数一致，没有考虑空间因素与影响因素之间的关系，对于空间位置差异性研究较少。

为了更好地解释空间异质性，Brunsdon 提出了地理加权回归模型（Geographically Weighted Regression,GWR）[20]，该模型因具有良好的拟合优度得以广泛应用，如用于解释出租车客流[21]、公交客流[22]的空间分布等。为了更好地衡量不同区域截面参数的空间异质性，本文引入地理非平稳性概念，通过GWR 模型来分析外在因素对共享单车分布特征的影响及其空间异质性。

1 数据来源与影响因素选取

本文拟采用共享单车GPS 数据来分析共享单车的出行分布特征。共享单车数据主要来源于Python 每5min 爬取到的2018 年9 月28 日（星期五）整个西安地区停放的某品牌单车GPS 位置数据，获取的数据字段包括采集时间、单车编号、单车经纬度，示例见表1。

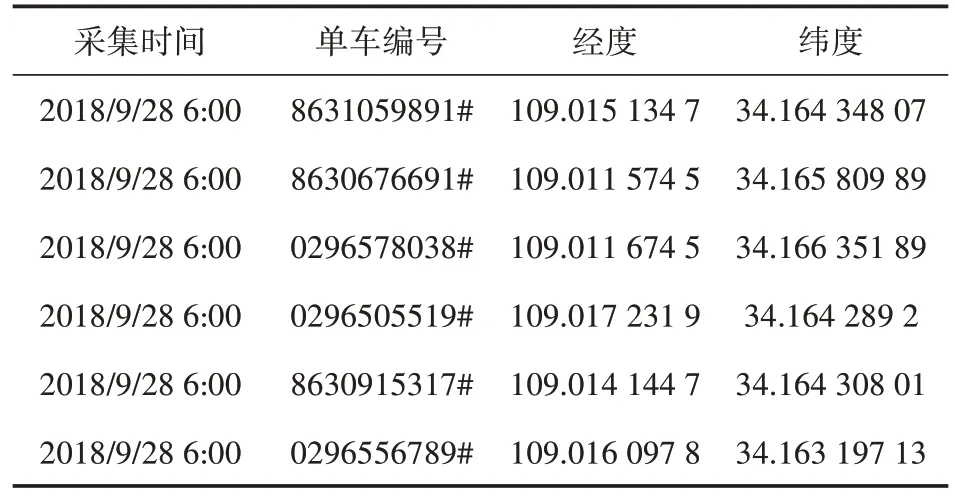
表1 原始数据示例

从研究区域的社会、经济、基础设施等实际状况出发，结合已有文献中对自行车骑行特征及其影响因素的探究，总结分析得到以下4 类影响因素。

（1）用车环境。已有研究表明共享单车停放点的数量与容量的增加会促进单车出行[11]。此外，共享单车设施（主要指出行产生前交通小区内的共享单车）分布密度与非机动车道的覆盖情况在很大程度上决定着用户的二次骑行意愿，因此用车环境是否便捷舒适成为了解共享单车出行分布特征的一个重要指标。

（2）道路交通基础设施。城市道路等级密度、长度、连通性等指标将直接影响用户体验及对出行方式的选择，进而影响单车分布状态。有学者就不同类型的道路长度对共享单车出行的影响进行了分析，认为主干路的长度会对单车出行产生负面影响，而支路长度在一定程度上会促进单车出行[23]。

（3）公共交通变量。共享单车停放点与交通枢纽点（如火车站、客运站、轨道交通或常规公交站点）间的最短路径长度、共享单车停放点辐射区内的公交站点数量和类型等指标在不同程度左右着出行者对出行方式的选择。若共享单车与其他公共交通站点衔接并不理想，可能对骑行产生负面影响。

（4）土地利用变量。根据已有研究可知，就业情况对共享单车的分布具有一定影响[24]，而土地利用影响具体的就业分布。此外，土地利用类型较为多样化的区域将会有较高的出行需求产生[23]，常用的生活服务设施、消费场所及休闲娱乐场所等其他服务设施的分布差异也会引起共享单车出行起讫点有规律地差异分布。

综合上述分析，依据所需数据采集的难易程度及数据可靠性，选取能反映研究区域内共享单车分布特征的影响指标，如图1所示。

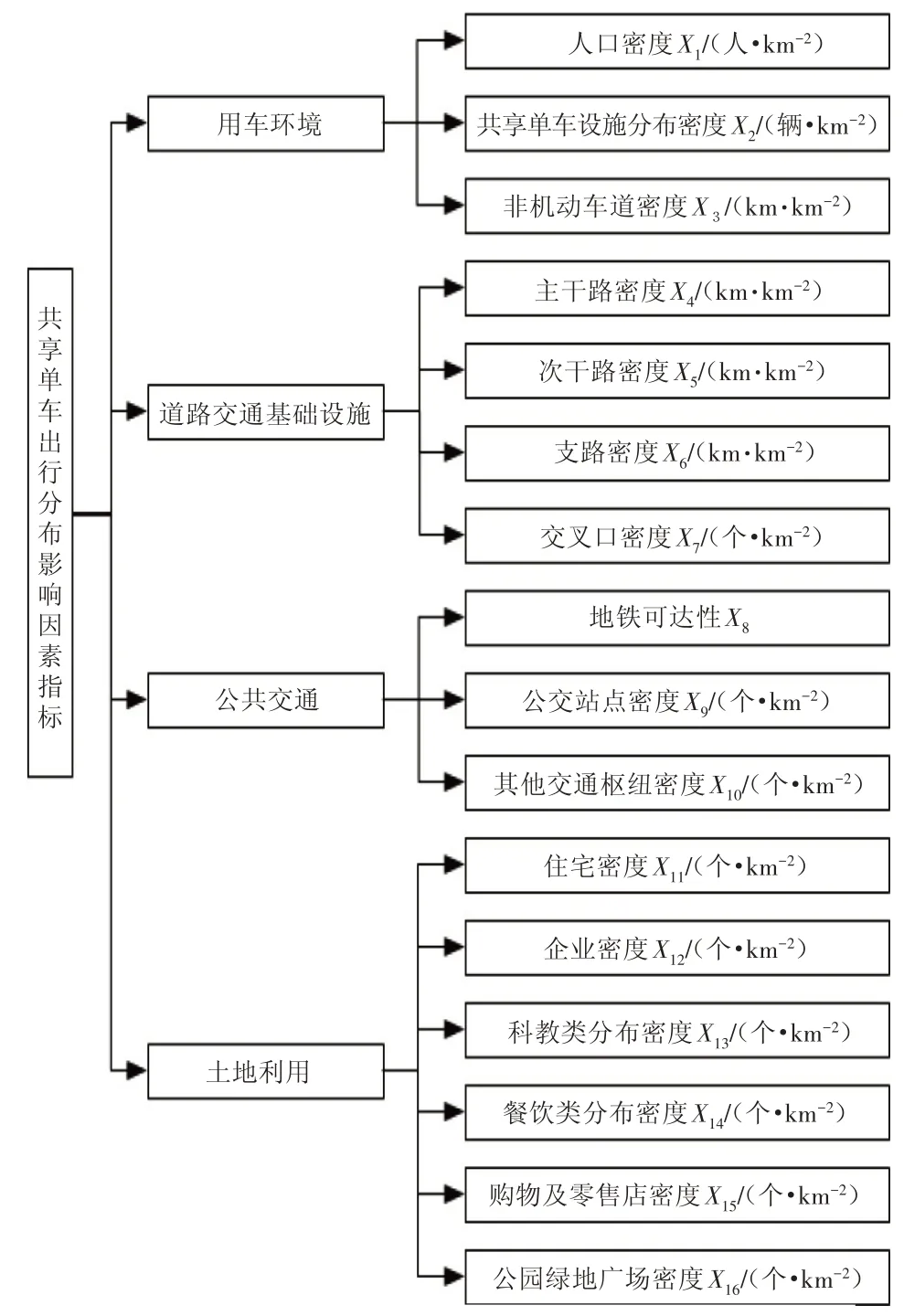
图1 共享单车出行分布的影响因素

图1 所示影响因素中，共享单车设施分布密度指出行产生前交通小区内的单车分布密度；人口数据和城市路网等矢量数据来源于西安市城市交通模型，经过提取计算得到各小区的目标要素；X9～X16均为对获取的兴趣点（Point of Interest,POI）数据进行处理后得到的有效数据；地铁可达性SubAr的计算公式[25]为：

2 模型建立

本文首先建立多元线性回归模型对影响因素进行全局回归分析，初步筛选得出影响较为显著的变量。考虑到部分因素随着时间及空间的变化，其对因变量的影响程度也会有所差异，故进一步通过构建地理加权回归模型（GWR），对变量进行空间异质性检验，并比较这两种回归模型的拟合效果。

2.1 全局回归模型

在进行多元线性回归时，为避免参数估计值发生严重偏差，需对备选自变量间的多重共线性进行检验，以保证解释变量的独立性，提高模型估计的准确度。本文采用方差膨胀因子（Vari⁃ance Inflation Factor，VIF）作为检验工具，以剔除不符合要求（VIF较大）的影响因子。

多元线性回归模型用两个或多个自变量来解释因变量的变化，且可以用普通最小二乘法（OLS）求解各变量对应的系数。该模型计算公式为：

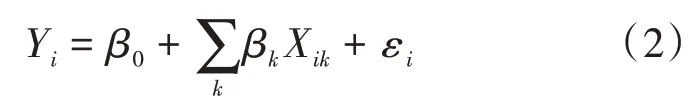
式（2）中：Yi为第i个样本点的因变量（早晚高峰单车出行起讫点）；β0为线性回归方程的截距（常数项）；βk为第k个自变量（影响因素）的回归系数；Xik为第i个样本点的第k个自变量；εi为随机误差项。

2.2 地理加权回归模型

空间显著性相关是GWR 模型的使用前提条件，为便于后续空间计量经济模型的构建与参数估计分析，本文采用Moran′s I（莫兰指数）对各解释变量进行空间自相关性分析。Moran′s I 是用来度量空间相关性的一个重要指标，经归一化处理后，取值为（-1,1）。Moran′s I大于0表示空间正相关，其值越大则空间相关性越强；Moran′s I小于0 表示空间负相关，其值越小则空间差异越大；Moran′s I 等于0，表示空间不具有相关性。GWR模型是在传统线性回归模型的基础上改造模型系数，纳入表示地理位置的参数，根据研究区域的空间变化对各变量进行局部回归分析。本文选用GWR 模型对共享单车空间分布的影响因素进行进一步探讨，其计算公式为[20]：

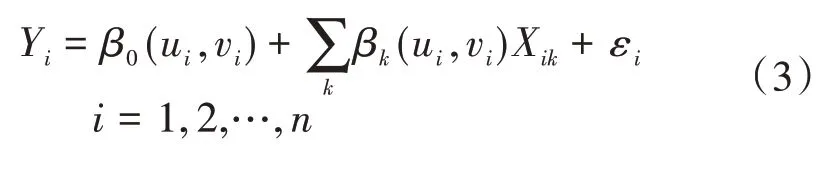
式（3）中：(ui,vi)为第i个样本点的空间经纬度坐标点；εi为随机误差项，εi～N(0,δ2),Cov(εi,εj)=0(i≠j)；n为样本量。

模型的实现流程如下：

（1）确定最优带宽。带宽b用来解释wij（空间权重）与dij（样本点i与j距离）之间的函数关系。带宽b过大将会导致不同区域间的参数估计值差异不明显，影响模型参数估计值的准确性；而过小的带宽则会导致方差变大[21]。赤池信息准则（Akaike Information Criterion,AIC）是衡量统计模型拟合优良性的标准之一，本文选用修正后的AIC，即AICc 来确定最优带宽，当函数值AICc最低时，模型最优，AICc计算公式为：

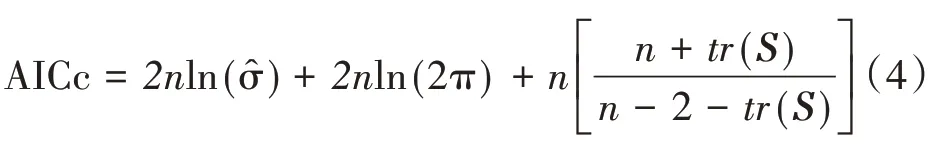
（2）选取空间权函数。空间权重函数的选择将决定空间权重矩阵的大小，自适应型权重函数可随回归点周围的样本点密度作相应的调整，而双重平方函数可剔除距离回归点较远且对回归点几乎无影响的样本点。由于本文研究区域内的样本数据分布不均匀且可能存在距离远到可忽略的点，因此选择自适应型双重平方函数进行回归分析[22]。wij(1 ≤j≤n)是空间权重函数[27]，其计算公式如下：

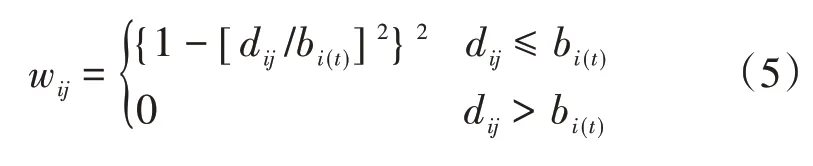
式（5）中：bi(t)为自适应型带宽，表示样本点i的t个临近点的最优带宽。

（3）计算回归系数。根据局部加权最小二乘法可得到模型的各回归系数。参数估计方法计算公式如下：

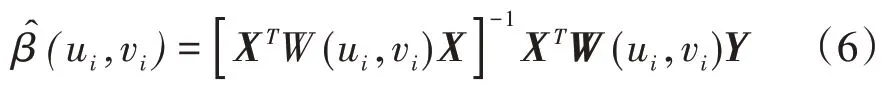
式（6）中：空间权重矩阵是W(ui,vi)一个n × n对角阵,W(ui,vi)=diag(Wi1,Wi2,…,Wij,…,Win)；X,Y分别为自变量与因变量矩阵；为模型参数估计值。

通过地理差异测试对某个特定的变量系数进行异质性检验，如果原模型优于比较切换的模型（采用AICc比较准则），则可判断该变量具有空间异质性。

3 结果与分析

3.1 模型结果及比较

以西安市主城区内的共享单车骑行数据为例，通过建立多元线性回归模型对建成区环境影响因素进行全局回归分析。在进行模型分析前，首先对各变量进行多重共线性检验与空间自相关性分析。共线性检验结果显示：各影响因素作为因变量时对应的方差膨胀因子均小于5，表明各变量均具有较高的代表性；空间自相关性分析结果显示：除其他交通枢纽密度X10外，各变量的Moran′s I 和聚集特性值z均为正，且显著性水平均小于0.05，表明除其他交通枢纽密度因素外，各变量间空间显著相关且空间分布具有较强的聚集性，因此剔除X10而保留其余变量进行全局回归分析。全局回归分析结果如表2～表5 所示。经过多次回归分析，初步筛选得到研究区域内工作日早晚高峰共享单车出行起讫点分布的显著影响因素（p＜0.05，显著水平α=0.05），如表6所示。

表2 工作日早高峰出行起点分布多元线性回归分析结果

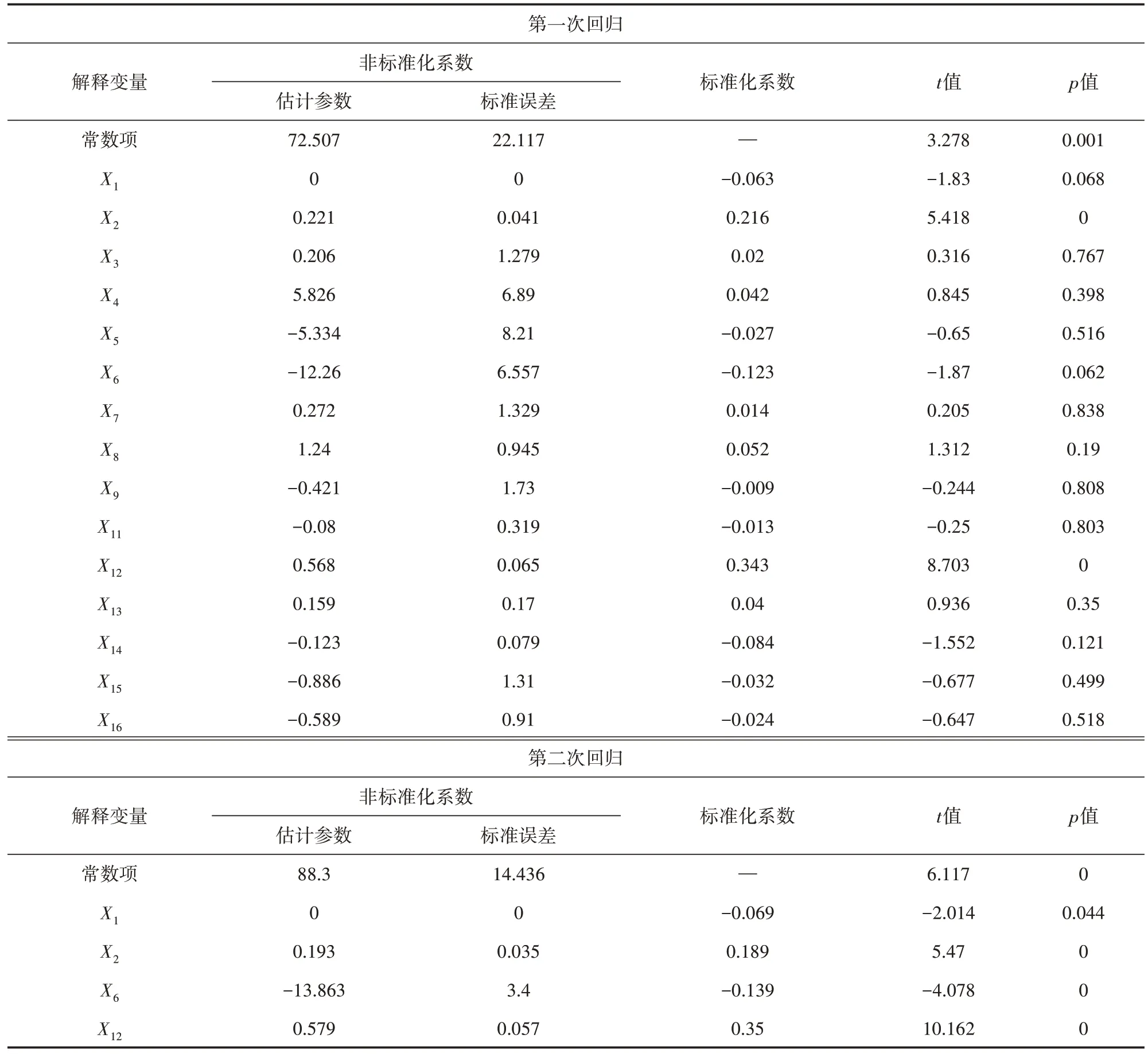
表3 工作日早高峰出行终点分布多元线性回归分析结果

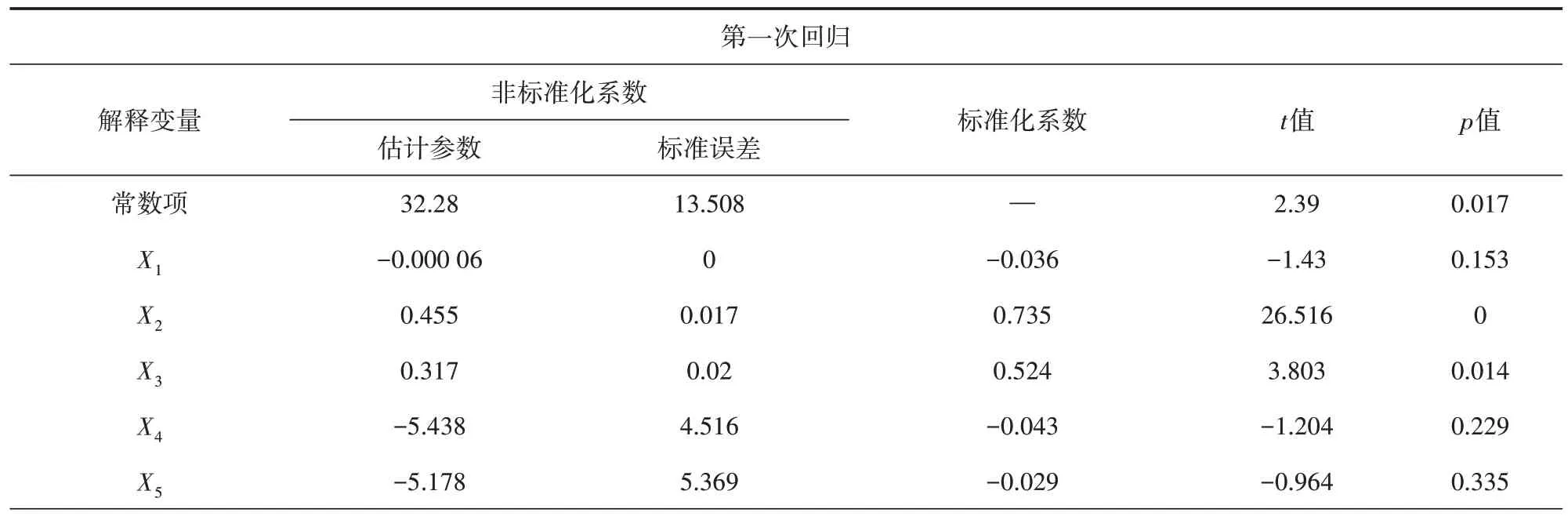
表4 工作日晚高峰出行起点分布多元线性回归分析结果

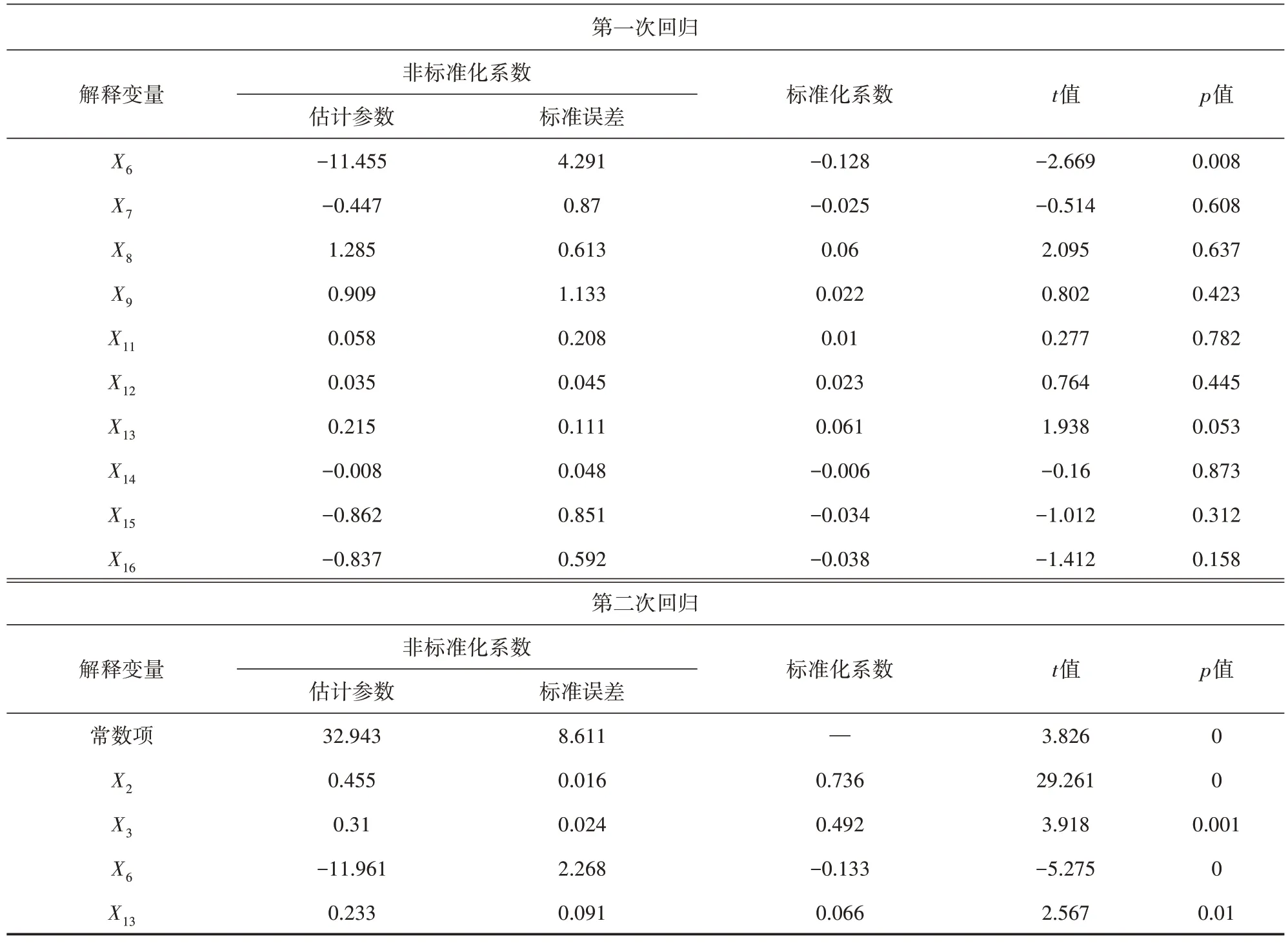
表4 （续）

表5 工作日晚高峰出行终点分布多元线性回归分析结果

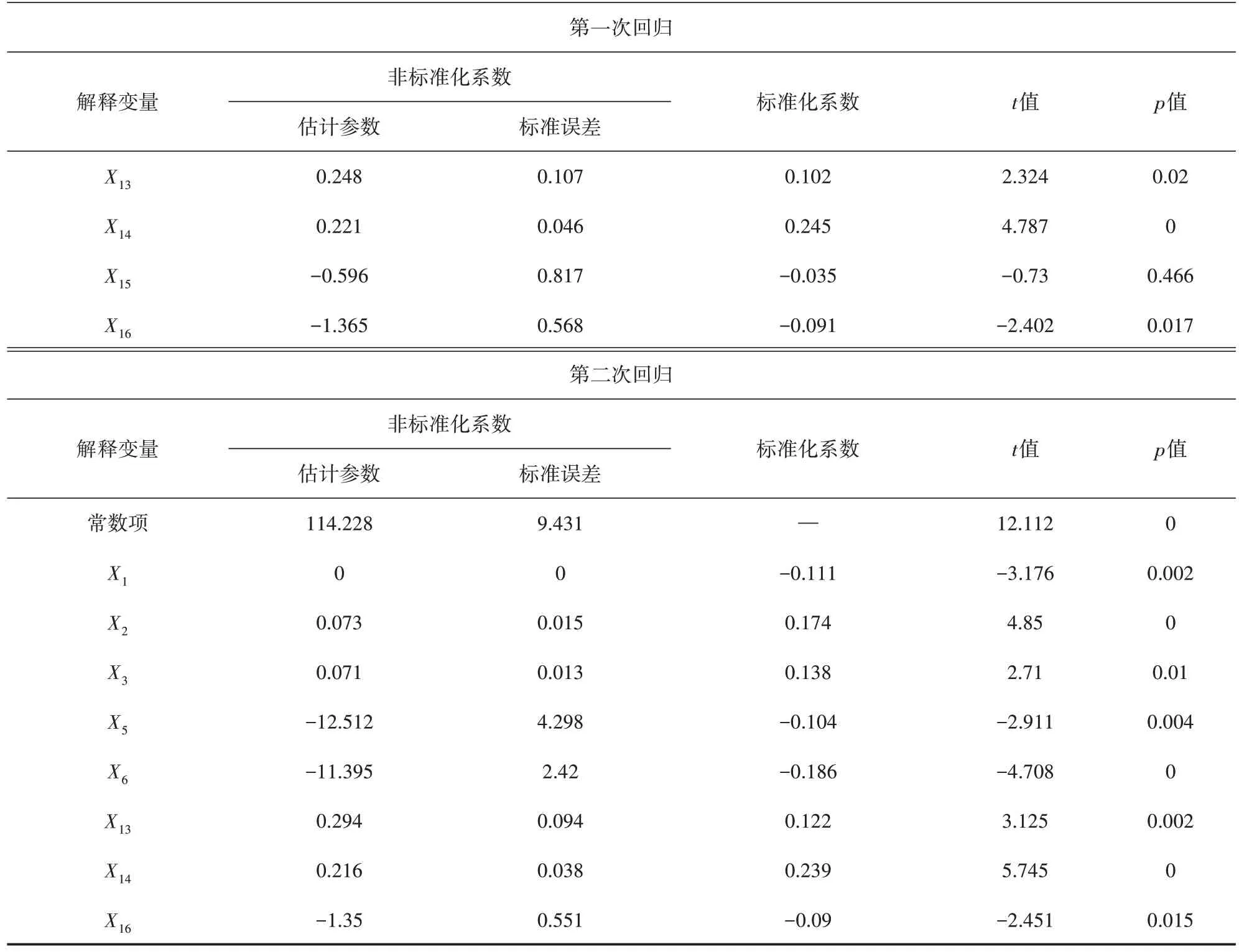
表5 （续）

表6 多元线性回归模型分析结果

为了确定上述各显著性影响因子是否具备空间异质性，需构建GWR 模型以得到模型的参数估计值（见表7～表8）。表7～表8中各统计量表示自变量对工作日早晚高峰共享单车出行起终点分布的影响程度。其中，模型参数估计为正值时，表示该解释变量与因变量正相关；模型参数估计值为负值则相反，且随着参数绝对值的增大，影响越大[28]。

GWR 模型拟合参数分析结果如表9 所示，分析得到在不同时段对共享单车起终点分布的影响具有较为显著的空间非平稳性的因素，即这些因素的空间关系可能是不稳定的。

表7 早高峰时段GWR 模型参数估计统计表

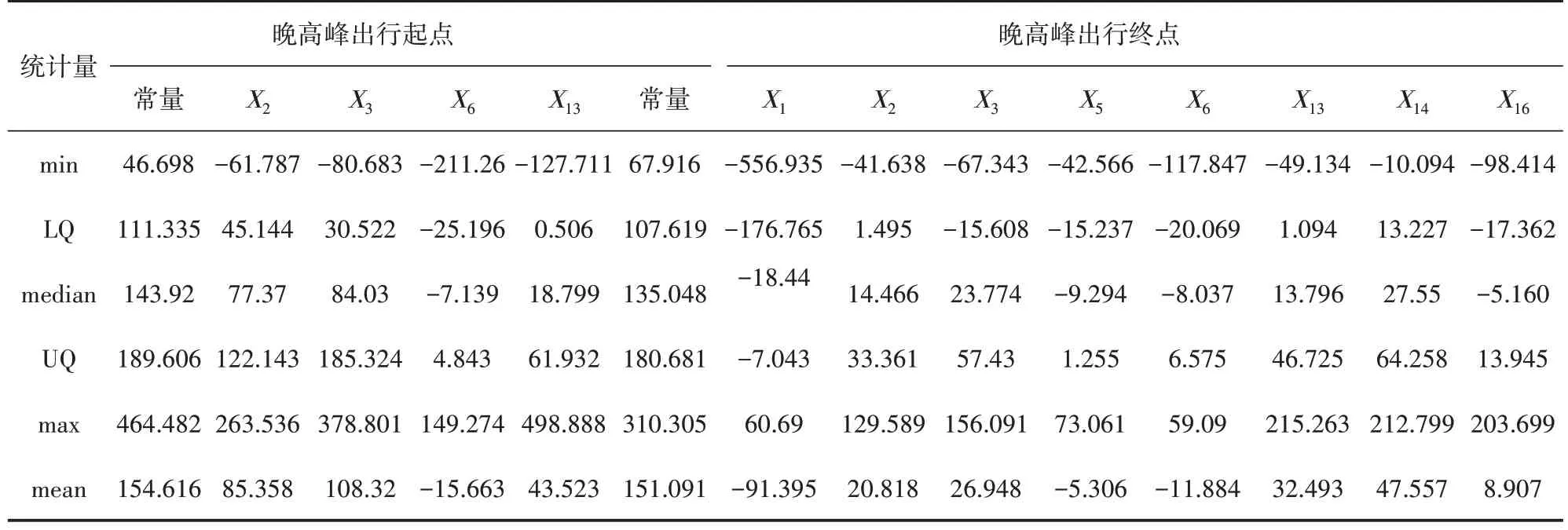
表8 晚高峰时段GWR 模型参数估计统计表

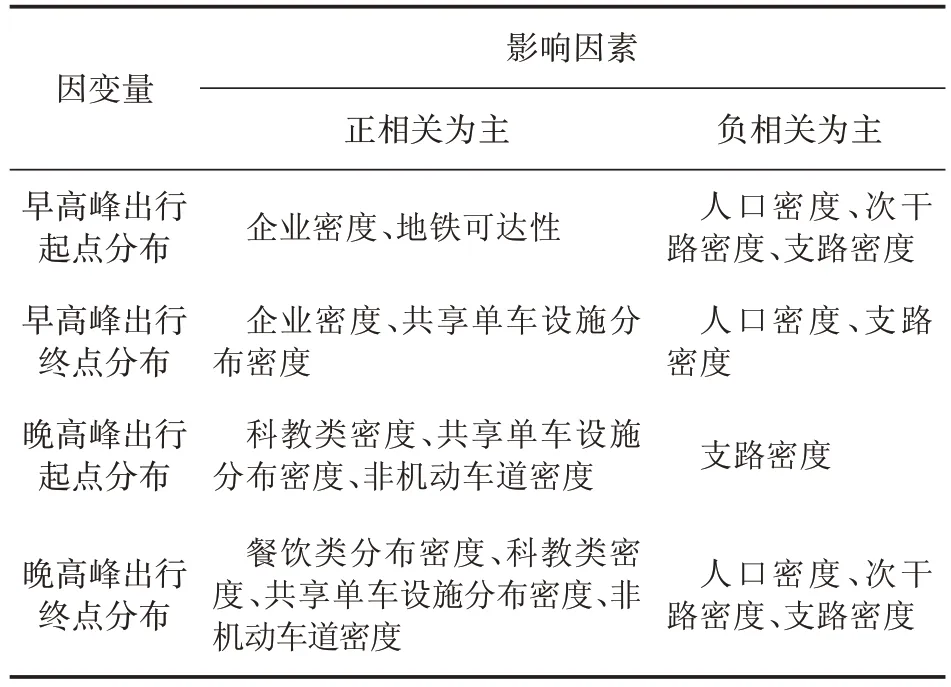
表9 GWR模型拟合参数分析结果

同时利用GWR 4.0 软件中的地理差异测试（Geographical Variability Test）功能对各变量（见表6）系数的异质性进行检验。地理差异测试通常用来识别局部与全局性影响因素，该测试通过对两个GWR 模型（第一个是将某一个变量作为全局变量，将其他所有变量作为局部变量的GWR模型；第二个是将所有变量作为局部变量的GWR模型）的AICc 值进行比较，如果第二个模型的AICc 值小于第一个模型，判断标准（DIFF of Cri⁃terion）值小于0，则该变量是因变量的局部影响因素（即具有空间异质性），否则该变量为全局影响因素。本文进行多次回归分析，剔除不具备空间异质性的影响因素（DIFF of Criterion 为正的因素），最终得到：在对工作日早高峰出行起点、终点与晚高峰出行起点、终点分布影响因素的测试中，DIFF of Criterion 小于0 的影响因素分别为共享单车设施分布密度（-158.186913）、企业密度（-221.139065）、共享单车设施分布密度（-229.317614）、餐饮类密度（-34.104404），即表明在工作日早高峰和晚高峰时段，共享单车设施分布密度对共享单车出行起点的影响均具有空间异质性；企业密度在工作日早高峰时段、餐饮类分布密度在工作日晚高峰时段对单车出行终点分布的影响存在空间异质性。另外，由于单车投放量对单车骑行率影响较大，车辆投放不足的区域难以单纯从骑行轨迹数据的挖掘中发现实际的骑行需求特性，导致GWR 模型影响因素的空间异质性不显著，因此应不断追踪单车投放量与GWR模型的时空拟合程度。

在使用两种模型对各变量进行回归分析后，为验证所选用模型的有效性与准确性，本文主要选取了拟合优度R²、调整后的R²、AICc值以及残差平方和4 个指标来考量模型的有效性，其中R²值与调整后的R²值越高，AICc值与残差平方和越小，说明模型的精度越高[29]。如表10所示，GWR模型分析结果中的R²和调整后的R²均高于全局回归模型中的数据；在工作日早、晚高峰时段，GWR模型对单车起终点回归分析的R²比全局回归模型分别提高了0.428,0.378,0.208 和0.309；同时，GWR 模型的AICc 值与残差平方和均小于全局回归模型。综上可知，GWR模型在回归分析中考虑了地理空间要素的影响，具有较强的有效性与准确性，较全局回归模型更适用于本研究。

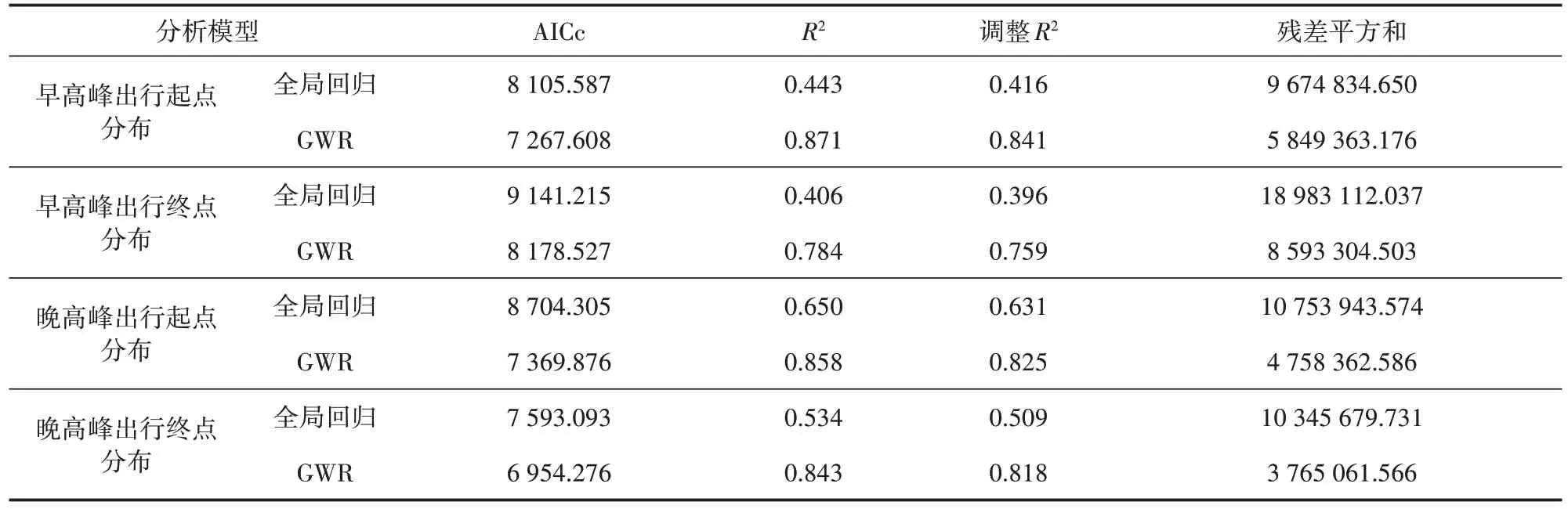
表10 OLS与GWR模型的比较结果

3.2 结果分析

结合3.1 节模型估计结果中具有空间异质性的显著变量，通过可视化分析工具从早、晚高峰出行起点及早、晚高峰出行终点两方面对研究区域内共享单车的分布差异及其内在原因进行详细梳理。

（1）出行起点

模型估计结果表明，在工作日早、晚高峰时段，共享单车设施分布密度对单车出行起点分布的影响具有空间异质性，估计参数空间分布如图2所示。共享单车设施分布密度因素在西安市南、北部区域对单车的分布表现为较强的促进作用，而在中部及东部地区表现为抑制单车出行。在北部区域，共享单车设施分布密度对单车分布的促进作用在早高峰时段更为明显。在南部区域，早高峰出行起点的促进区域相对于晚高峰分布更为集中。上述分布差异的原因在于西南区域的学校、企业、商业居多（例如小寨商圈及各大高校的分布），产生了较高的单车使用需求，共享单车设施分布密度便成为促进或抑制单车出行的一个重要指标；而东北角以及中心区域开发尚未成熟（如大明宫、汉长城），共享单车的投放量较低，因此对单车的使用产生较强的抑制作用。

（2）出行终点

企业密度与餐饮类分布密度估计参数空间分布如图3 所示。从中可看出，在西部区域，企业密度对早高峰单车出行终点的分布具有明显的促进作用，这与该区域内较为密集的企业分布、公共交通覆盖不足（相对稀疏的公交线网与轨道交通站点）等原因密不可分；中部及东北区域的企业密度对早高峰共享单车出行终点的分布具有显著抑制性，可能与该区域内企业分布较少有关，公交、地铁和私家车成为主要出行方式。

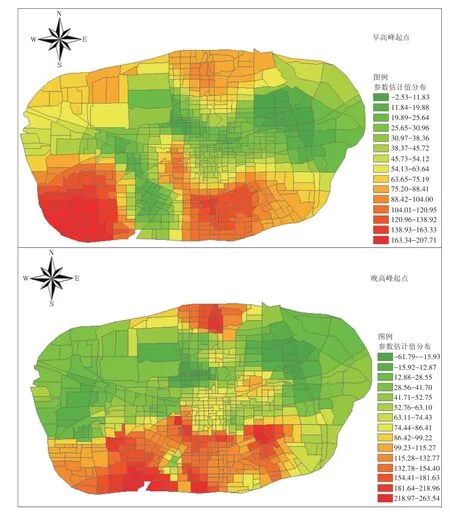
图2 共享单车设施分布密度估计参数空间分布

另外，在晚高峰时段，中心区域的餐饮类分布密度相对于外围区域对共享单车出行终点的影响表现出更强的抑制性。这是由于中心区域较为发达，餐饮分布较密集，公共交通等设施发展较为完善，为用户出行提供了较多的出行方式选择，因此餐饮类分布密度对单车出行的吸引相对较弱；而外围区域分布有较多的工业、科技园区且餐饮类分布较为分散，从而产生大量以就餐为目的的骑行需求。

4 结语

本文从城市建成区环境因素出发，综合确定影响共享单车出行分布的4 类因素，通过构建多元线性回归模型对各指标进行全局回归分析，剔除无关变量，得到影响共享单车出行起讫点分布特征的显著性指标，根据模型分析结果可判断出各指标对因变量的作用程度及方向（正相关或负相关），有利于决策者了解单车骑行环境的优劣状态。

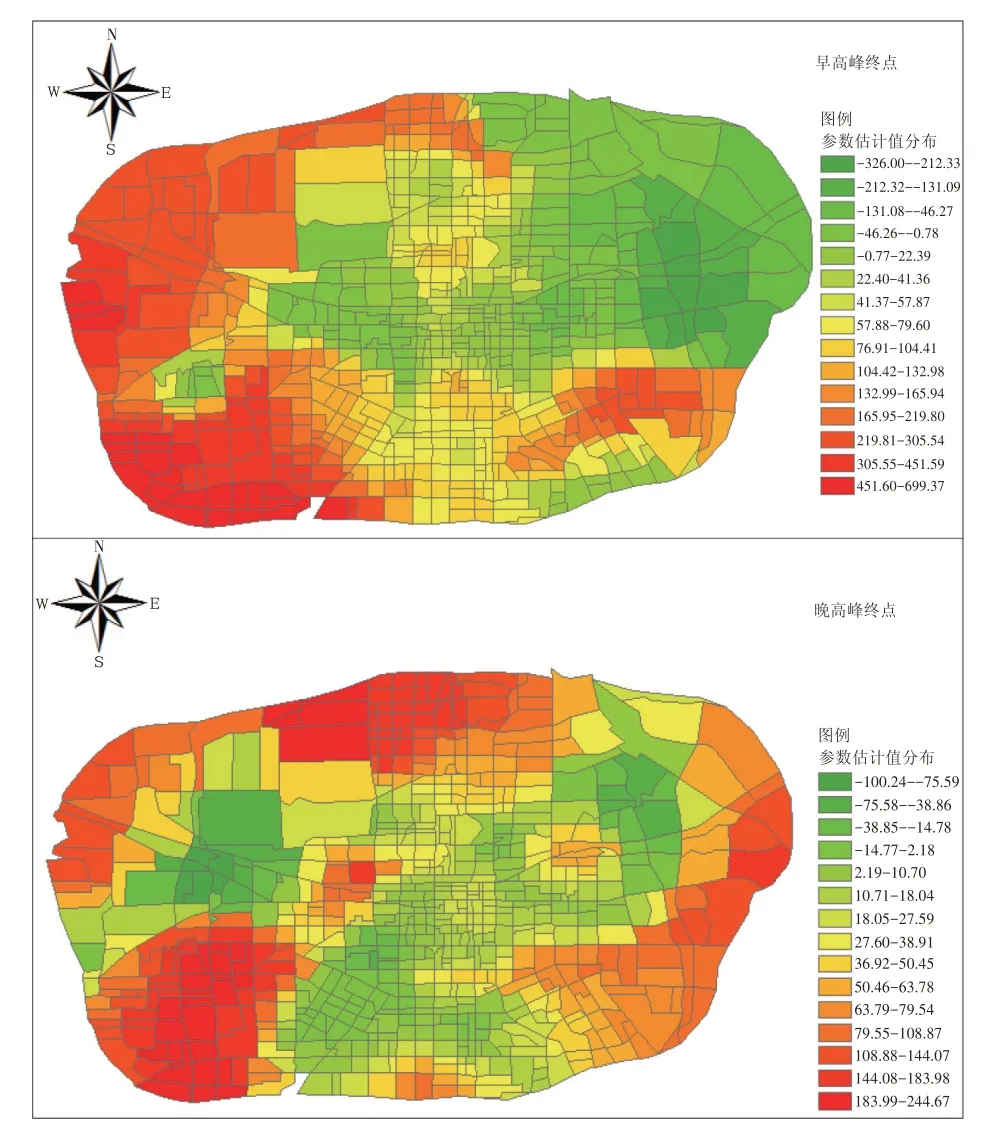
图3 企业密度与餐饮类密度估计参数空间分布

通过构建地理加权回归模型，根据模型的参数估计结果，可判断各影响指标所具有的空间非平稳性，并利用地理差异测试，剔除全局性影响因素，得出工作日各时间段（早、晚高峰）内共享单车出行起讫点分布的空间异质性因素，可为如何进行资源配置以更好地满足不断变化的用户需求提供参考。

通过对西安市主城区的共享单车出行数据进行模型拟合可知：在工作日早高峰和晚高峰时段，共享单车设施的分布密度对单车出行起点分布的影响具有空间异质性，而企业密度在工作日早高峰时段、餐饮类分布密度在工作日晚高峰时段对共享单车出行终点分布的影响存在空间异质性。对这些因素进行可视化分析，决策者可直观地看出不同时空下影响单车出行OD 的关键因素，以选取合适的改善方案来提高用车率。

在后续的研究中，可将个体属性等因素纳入研究范畴，以提高变量的解释能力，为管理者提供更科学合理的决策支撑依据，为共享单车的投放和调度提供更具针对性的指导。