具有部分缺失数据混合伽马分布参数的估计
2021-03-06于新龙王婷婷
于新龙,王婷婷,杨 航
(吉林师范大学 数学学院,吉林 四平136000)
0 引言
在统计学中,伽马分布是一种重要的连续概率函数,在交通安全理论中也有着重要作用.近年来,研究学者们也对这类分布的统计性质进行了各种研究.文献[1]对伽马分布的形状参数进行了估计,并且给出了该估计在交通流演化规律中的一些应用;文献[2]给出了对数伽马分布的尾部性质;文献[3]研究了在损失函数下逆伽马分布参数的Bayes估计问题;文献[4]讨论了在样本数据不完全情形下,利用极大似然估计方法对两个伽马分布总体参数进行统计推断;而文献[5-7]研究了多种分布在数据缺失样本下的相关算法及置信区间问题.本文通过对上述文献的研究,提出了在具有部分缺失数据下的混合伽马分布总体的参数估计问题,主要通过矩估计法,证明了估计的优良性,并且建立了混合伽马分布总体参数相等的检验统计量.最后,利用随机模拟给出两参数估计的均方误差,通过观察均方误差的大小,来说明该估计的优劣.
1 矩估计及其渐进性质
假设混合伽马分布,其密度函数为:
其中,总体的未知参数为θi>0(i=1,2),α>0为已知参数,对两个混合伽马分布进行n次独立观测,在进行观测的时候,每一个样本以1-Ρ的概率缺失.总体观测值为(Xi,δi)(i=1,2,…,n).其中Xi表示混合伽马分布总体的第i个样本观测值,若第i个样本值丢失,则δi=0,否则δi=1.
下面考虑θ1,θ2的矩估计.基于样本观测值为(Xi,δi)(i=1,2,…,n),我们可以建立如下的矩估计方程:
其中
解方程得:
对上述参数θi(i=1,2)的矩估计,下面证其相合性和渐进正态性.

证明 因为{Xi,δi,1 同理可得: 从而可得: θ2,a.s. 定理2在上述记号下,有: 令Σ=E(W1-EW1)(W1-EW1)T,于是由多元中心极限定理可得: 令: 从而可得: g1(T1n,T2n,T3n)= 由引理1知: 且 同理令: 根据引理1 其中: 在现实中 ,我们常常会注重两样本是否来自同一总体,此类问题可转化为检验混合总体参数是否相等的问题.考虑下面假设检验: H0:θ1-θ2=0↔H1:θ1-θ2≠0. 在原假设成立下,有: 其中: 下面通过Matlab编程进行随机模拟,来说明此方法的可行性.当已知参数α=2时,分别给定样容量n=100,n=300,n=500,混合概率q=0.7,缺失概率1-P=0.1的模拟研究结果,其中在给定不同参数真值θ1,θ2时,各参数估计的均方误差随机模拟1 000次的平均值如表1所示. 表1 模拟结果 根据模拟结果可以看出,无论样本量较大还是较小,参数估计的均方误差都比较稳定,在可接受的范围内,因此说明此方法具有一定的可行性.
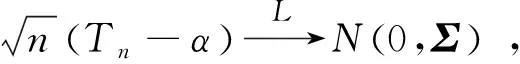



2 混合总体参数相等的检验和混合总体参数之差的渐进置信区间
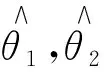

3 模拟研究

