两项分数阶微分控制的非线性Duffing 振子共振特性研究

2021-03-05孙健华丁维高

机械设计与制造 2021年2期

孙健华，魏巍，丁维高，谢进

（西南交通大学机械工程学院，四川成都 610031）

1 引言

在机械振动学[1]、能量俘获[2]、信号检测[3]等领域中许多物理系统的计算模型均为Duffing 振子。当Duffing 振子系统受到的外加激励频率与系统的固有频率接近时，系统会出现主共振现象；另外，Duffing 振子的分岔、混沌运动及其运动控制一直是工程科学研究的重要课题。

目前，针对于Duffing 振子的运动控制问题已经有了许多研究成果[4-6]。近年来，利用分数阶微积分控制项的控制技术引起了广泛的关注。研究表明：该项控制技术能够有效地改善控制器的控制效果，提高控制系统的鲁棒性[7]。就Duffing 振子的运动及其控制而言，文献[8]研究了受单项分数阶微分控制的Duffing 系统，研究表明：增大分数阶微分项的系数和阶次可使系统的共振振幅和共振频率同时减小；文献[9]设计了基于速度的分数阶PID 控制器，使控制器的比例、积分、微分环节以等效线性阻尼、等效线性刚度或等效质量的形式，对非线性Duffing 振子的混沌运动、共振振幅和共振频率施以控制。

文献[10]研究了受两项分数阶微分控制的单自由度线性振子的控制。研究表明：采用两项分数阶微分控制项，不但可以增加控制参数的可调范围，而且可以在减小线性振子系统的共振幅值的同时增大线性振子系统的共振频率。

基于上述分析，提出将基于振子位移的两项分数阶微分控制项施加于非线性Duffing 振子系统中，以期实现Duffing 振子的稳定运动，同时达到减小Duffing 振子共振幅值、共振频率的目的。

2 受两项分数阶微分控制项的Duffing振子系统动力学方程及其近似解析解

非线性Duffing 振子的动力学方程为：

式中：m—系统质量；x—系统振子的位置；k1—线性刚度；k2—非线性刚度；c—线性阻尼；F—外加激励力幅值；ω—外加激励频率。

将两项分数阶微分控制项同时引入到非线性Duffing 振子系统中，得到：

式中：ce，ke—系统（2）的等效阻尼和等效刚度。

在两项分数阶微分控制系统的设计中，实际上是通过改变分数阶微分项系数KD1、KD2和阶次p3、p4的取值，实现对系统等效阻尼和等效刚度的调整，进而达到对Duffing 振子的运动进行控制的目的。

等效阻尼ce和等效刚度ke随分数阶微分项系数KD1、KD2和阶次p3、p4的变化规律，如图1 所示。从图1（a）可见：KD1与等效阻尼ce、等效刚度ke之间均为线性关系，且随着KD1增大，两者同时增大；从图1（b）可见：KD2与等效阻尼ce、等效刚度ke之间均为线性关系，且随着KD1增大，等效阻尼ce增大，而等效刚度ke减小。对比图1（a）和图1（b）可以发现：图1（b）直线的斜率大于图1（a）直线的斜率，说明KD2对等效阻尼ce和等效刚度ke的影响要大于KD1的影响。从图1（c）及图1（d）可见，等效阻尼ce和等效刚度ke随阶次p3、p4的变化均呈现出非线性的变化规律，而且，p4的变化对于等效阻尼ce和等效刚度ke的影响要大于p3的影响。

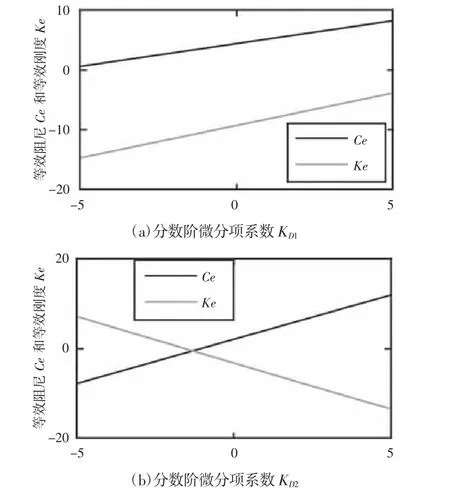
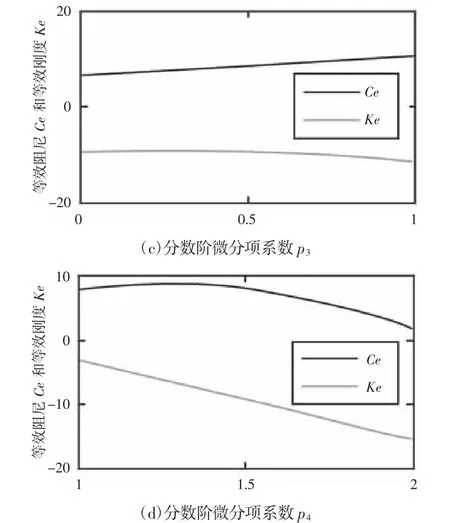
图1 分数阶参数对系统等效阻尼ce 和等效刚度ke 的影响Fig.1 Effects of Fractional-Order Parameters on Equivalent Damping ce and Equivalent Stiffness ke

3 系统定常解及其稳定性分析

由式（10）可得：

取非线性Duffing 振子系统的参数m=5，c=0.2，k1=15，k2=1，F=3，ε=0.05，图2 中的虚线所示为无任何控制的Duffing 振子幅频曲线。从图中可见，当ω＞2.0 的时候，对应于同一个ω 值有（2～3）个稳态的幅值，因而，系统会出现了幅值跳跃现象，说明振子的运动是不稳定的。若将满足定常解稳定条件的分数阶微分控制项加入系统中，即满足式（15）的分数阶微分参数：p3=0.4、p4=1.5，KD1=3、KD2=2，可以得到在分数阶微分控制下的幅频响应曲线，如图2 中的实线所示。图中的幅频响应曲线说明：满足式（15）的分数阶微分控制可以消除幅值跳跃现象，使振子处于稳定振动的运动状态。

利用式（15）及上述各个参数之间的关系，还可以根据期望共振振幅a*和共振频率ω*确定出分数阶微分控制项的参数。例如：a*＝0.6，ω*＝2，相位角θ=－45°。首先取p3=0.5，p4=1.5，由式（15）可以得到KD1=3.365，KD2=－1.37225。显然，对于同一组a*及ω*，可以有多组的分数阶微分控制的参数可供选择，这样就为提高和改善控制器的效能提供了宽阔的空间。

4 分数阶微分控制项参数的取值对系统振动频幅的影响

鉴于两项分数阶微分控制项中4 个参数均对Duffing 振子的运动有不同程度的影响，在本小节中，将利用第3 节中得到的近似解析解，分析分数阶微分系数KD1，KD2及阶次p3，p4四个参数的取值对共振振幅和共振频率的影响。在分析中选取Duffing 振子系统的参数为m=5，c=0.2，k1=15，k2=1，F=3，ε=0.05；如果没有特殊说明，分数阶微分控制参数为KD1=3，KD2=2，p3=0.4，p4=1.5。

4.1 参数KD1 对共振振幅和共振频率的影响

分别取KD1为1，2，3，4，5 时，系统的幅频响应，如图3 所示。对应的共振频率和最大共振幅值，如表1 所示。

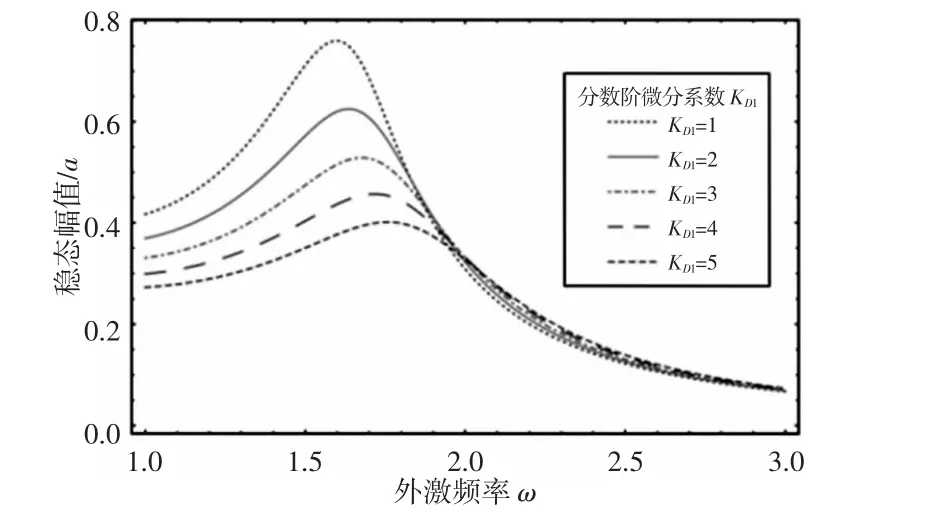
图3 KD1 变化时幅频响应曲线Fig.3 Effect of KD1 on Amplitude-Frequency Response Curves

表1 参数KD1 对应共振频率和共振幅值Tab.1 Parameter KD1 Corresponds to Resonant Frequencies and Common Amplitudes Value

从图3 和表1 可知：随着分数阶微分系数KD1的增大，Duffing振子共振时最大稳态幅值逐渐减小，同时，系统共振频率逐渐增大。由图1（a）可知，KD1增大，等效阻尼ce和等效刚度ke均增加。等效阻尼增大，使系统共振振幅减小；等效刚度增加提高了系统的固有频率，从而使共振频率增加。总之，增大分数阶微分控制项系数KD1，能够减小系统的共振振幅，同时增大系统的共振频率。

4.2 参数KD2 对共振幅值和共振频率的影响

分别取KD2为1，2，3，4，5 时，系统幅频曲线，如图4 所示。共振频率和最大共振幅值，如表2 所示。

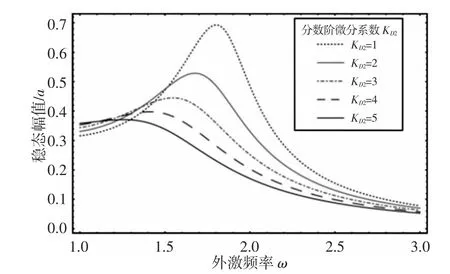
图4 KD2 变化时幅频响应曲线Fig.4 Effect of KD2 on Amplitude-Frequency Response Curves

表2 参数KD2 对应共振频率和共振幅值Tab.2 Parameter KD2 Corresponds to Resonant Frequencies and Common Amplitudes Value

由图4 和表2 可知：随着KD2的增大，系统发生主共振时最大共振幅值和共振频率都较小。由图1（b）可知，KD2增大，等效阻尼ce增大，然而等效刚度ke减小。等效阻尼增大减小了系统共振振幅，等效刚度的减小降低了系统的固有频率，使得系统共振频率降低。总之，增大分数阶微分控制项系数KD2，可以较大程度地减小系统的共振幅值和共振频率。

4.3 参数p3 对共振幅值和共振频率的影响

分别取p3值为0.2，0.4，0.6，0.8 时，系统幅频响应曲线，如图5 所示。对应的共振频率和最大共振幅值，如表3 所示。

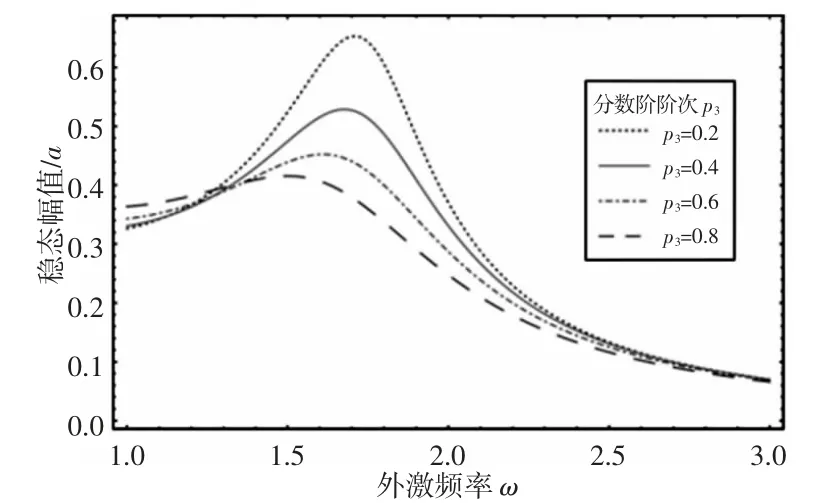
图5 p3 变化时幅频响应曲线Fig.5 Effect of p3 on Amplitude-Frequency Response Curves

表3 参数p3 对应共振频率和共振幅值Tab.3 Parameter p3 Corresponds to Resonant Frequencies and Common Amplitudes Value

由图5 和表3 可知：当阶次p3增大时，系统的主共振幅值逐渐减小，同时引起系统发生主共振的外加激励频率逐渐减小。由图1（c）可知，p3增大，等效阻尼ce增大，然而等效刚度ke减小。等效阻尼增大，减小了系统共振振幅，等效刚度的减小减低了系统的固有频率，使共振频率减小。总之，增大阶次p3，能同时减小系统的共振振幅和共振频率。