粉末高温合金涡轮盘初始缺陷概率模型研究

白国娟，侯乃先，杨 坤，陈 健

（1.中国航发商用航空发动机有限责任公司，上海201108；2.上海商用飞机发动机工程技术研究中心，上海201108）

1 引言

航空发动机限寿件是指其主要失效可能导致危害性发动机后果的转子和主要静子结构件，如盘、轴、轮毂等。并且，限寿件必须通过局方批准的程序指定其寿命[1]。在实际结构设计中主要通过降低限寿件的失效概率来提高整机的安全性。目前，国内普遍采用基于安全寿命的部件寿命管理方法来防止限寿件的失效[2]。安全寿命法在一定程度上提高了航空发动机的安全性，但是仍然无法有效避免灾难性事故的发生，如1989 年Sioux City 空难[3]和1996 年Pensacola 空难[4]。为此，美国航空界提出基于概率风险评估的部件寿命管理方法，从而降低限寿件的失效概率[5-7]。美国联邦航空局在适航规章中也提出了明确要求—发动机通过安全性分析确定限寿件后，必须通过风险评估表明限寿件在预期使用寿命期内的失效概率低于10-8次/飞行小时，只有满足要求的发动机才能获得最终的型号合格证[8-9]。因此，对限寿件在使用寿命期内的失效概率进行概率风险评估为航空发动机适航取证时必须表明的符合性要点之一。

涡轮盘作为航空发动机典型的限寿件，在使用寿命期内的失效概率必须进行概率风险评估。并且，随着航空发动机性能和推重比的提高，涡轮盘的工作条件越发严酷。涡轮盘材料由铸造合金到变形合金再到粉末合金。由于粉末合金的晶粒组织均匀性较好、有效避免了铸锻过程中产生偏析，从而材料塑性得到大大的提高，所以粉末合金已成为各种先进航空发动机涡轮盘首选材料。但是，目前的粉末冶金的工艺流程不可避免地会在成型部件中形成各类气孔、夹杂等缺陷。并且，这些微缺陷在循环载荷作用下易成为疲劳裂纹萌生点，有可能使实际疲劳寿命低于无缺陷假设下计算得到的寿命结果，从而大大增加了发动机在使用过程中发生涡轮盘意外破裂的风险[10-11]。这些缺陷作为概率风险评估的重要输入，是影响涡轮盘失效风险的最重要、最直接的因素之一。

近年来，越来越多的国内外学者基于概率的风险评估方法研究[12-14]。通过对缺陷形状、大小的统计及其与破坏的关联分析和假设，对概率破坏模型进行修正和推广。但是，很少有专门针对FGH96 粉末高温合金涡轮盘进行大批量的初始缺陷统计，得出其缺陷概率模型，分析缺陷形式，所以研究FGH96 粉末高温合金涡轮盘初始缺陷概率模型对FGH96 粉末高温合金涡轮盘概率风险评估有着重要意义。

因此，对国内FGH96 粉末高温合金涡轮盘进行初始缺陷检测，通过对其缺陷形状、缺陷大小的统计分析，得出缺陷面积、圆度、椭圆长短轴比概率模型，为FGH96 粉末高温合金涡轮盘概率风险评估提供数据支撑。

2 FGH96 粉末高温合金初始缺陷检测

对于粉末高温合金而言，初始缺陷主要采用在位鉴定检测进行检测，利用光学显微镜配合扫描电子显微镜（Scanning Electron Microscope，简称SEM）和能谱仪（Energy Dispersive Spectrometer，简称EDS）进行检测和分析。在位鉴定检测是在夹杂物、缺陷和合金的基体不分离的情况下进行检查。

2.1 试样制备

利用电火花切割机对FGH96 粉末合金进行截取制造试样，试样尺寸磨面面积约200mm2，高度约10mm。试样进行研磨之前，为了充分保护试样，对试样进行镶嵌处理，避免对试样造成破坏。试样用树脂镶嵌法对其进行处理[15]，利用自凝牙托粉和自凝牙托水进行的化学反应，按照一定比例混合对试样进行镶嵌处理。镶嵌后对试样进行研磨，最后进行抛光处理以达镜面，且无磨制缺陷。

2.2 初始缺陷检测

将试样制备好以后，放在扫描电镜下进行观察，其图像通过高分辨率扫描或摄像系统检测后，在高分辨率显示器上显示。通过比较组织与组织、组织与缺陷之间的灰度差来进行夹杂物和缺陷的检测与鉴别，根据鉴别图像上像素点的状态来完成测量。

检测时缺陷形状[16-20]有：圆形、椭圆形、细长形、大致方形，且绝大多数为椭圆形，或近似椭圆形。检测所得的缺陷图，如图1 所示。

图1 FGH96 高温合金材料初始缺陷Fig.1 Initial Defects of FGH96 Powder Metallurgy Superalloy

3 FGH96 粉末高温合金初始缺陷统计分析

在缺陷统计分析的过程中，主要对缺陷的形状、尺寸和面积进行统计。对于圆形缺陷，对其直径、面积等参量进行测量和统计；对于椭圆形缺陷，给出对应的长短半轴和面积参量；对于细长形缺陷，将其视为特殊的椭圆进行统计；对于大致方形缺陷，通过外接圆的方法对其进行转换折算。对于一些不规则的缺陷，需要进行特定的转换折算方式对缺陷的面积和尺寸进行统计。缺陷的大致尺度约为1μm 至50μm 左右，对于小于1μm 的缺陷，暂不予以考虑。

为了有效分析缺陷，采用Image-J 软件对由SEM 获得的缺陷图进行相应分析，确定缺陷的面积、圆度和椭圆度等参数，对缺陷进行描述和说明。面积表示每个缺陷的区域面积，圆度描述缺陷边界线接近圆形的程度，椭圆度是用来考察缺陷边缘形状与椭圆的符合程度，用长轴、短轴和短轴/长轴三个量表征。其中具体参数定义如下：

面积：描述真实缺陷面积大小。主要是利用像素统计法对256 色缺陷图中缺陷面积进行面积统计，逐级累加获得缺陷图中真实缺陷的面积大小。

周长：描述真实缺陷周长长短。主要利用算法对256 色缺陷图中的缺陷边缘进行周长计算，逐级累加获得缺陷图中真实缺陷的周长。

圆度：描述缺陷边界线接近圆形的程度，用于缺陷图像特征的提取与描述。圆形度为1 时，缺陷即为圆形；圆形度越小，缺陷则越不规律。

椭圆度：用来考察缺陷边缘形状与椭圆的符合程度，用长轴、短轴和短轴/长轴三个量表征，采用Image-J 内置的最小二乘法对缺陷图形进行椭圆拟合。其中长轴和短轴分别为采用最小二乘法拟合后的椭圆的长短轴，短轴/长轴为将细长目标与近似矩形或圆形目标进行区分时采用的形状度量，表征缺陷的形状。

α 为三参数威布尔分布位置参数；β 为尺度参数；γ 为形状参数，描述测量值的分散性。

3.1 缺陷面积统计分析

对于2054 个缺陷的面积统计结果进行分析，对于FGH96 粉末材料缺陷面积大部分都处于（1～5）μm2左右。对于缺陷面积的分布，拟采用三参数威布尔分布对其进行拟合。通过拟合计算和相关检验发现三参数威布尔分布符合性较好，拟合参数，如表1 所示。

表1 缺陷面积拟合参数Tab.1 Defect Area Fitting Parameters

通过对缺陷面积分布拟合，获得了相应的拟合函数参数。针对获得的拟合函数，分别进行K-S 检验、Anderson-Darling 检验，并进行相应评估。检验参数，如表2 所示。

表2 缺陷面积拟合函数检验参数Tab.2 Defect Area Fitting Function Test Parameter

对于缺陷面积拟合的三参数威布尔分布密度函数和分布函数，如表3 所示。缺陷面积密度函数和分布函数图，如图2、图3所示。

图2 缺陷面积密度函数拟合图Fig.2 Fitting Plot of Defect Area Density Function

表3 缺陷面积拟合函数Tab.3 Defect Area Fitting Function

图3 缺陷面积分布函数拟合图Fig.3 Fitting Plot of Defect Area Distribution Function

3.2 缺陷圆度统计分析

通过对缺陷的形状分析，缺陷形状大致可以分为三角形、正方形、圆形和长条形等四种。对于不同形状的缺陷，通过圆度来对缺陷进行评估，表征缺陷与圆的近似程度。圆度越接近1，表示缺陷越接近圆，裂纹扩展分析时用圆形缺陷模型。

通过对2054 个缺陷圆度进行分析统计，对于FGH96 粉末材料缺陷圆度大部分都处于（0.3～0.7）左右。对于缺陷圆度的分布，拟采用三参数威布尔分布对其进行拟合，具体拟合参数，如表4 所示。

表4 缺陷圆度拟合参数Tab.4 Defect Roundness Fitting Parameters

通过对缺陷圆度分布拟合，获得了相应的拟合函数参数。针对获得的拟合函数，分别进行K-S 检验、Anderson-Darling 检验和χ2检验，并进行相应评估，检验参数，如表5 所示。

表5 缺陷圆度拟合函数检验参数Tab.5 Defect Roundness Fitting Function Test Parameters

对于缺陷圆度拟合的三参数威布尔分布密度函数和分布函数，如表6 所示。缺陷圆度密度函数和分布函数图，如图4、图5所示。

表6 缺陷圆度拟合函数Tab.6 Defect Roundness Fitting Function

图4 缺陷圆度密度函数拟合图Fig.4 Fitting Plot of Defect Roundness Density Function

图5 缺陷圆度分布函数拟合图Fig.5 Fitting Plot of Defect Roundness Distribution Function

3.3 缺陷椭圆度统计分析

缺陷形状大致可以分为三角形、正方形、圆形和长条形等四种。在对FGH96 粉末材料进行裂纹扩展计算以及疲劳寿命预测等分析过程中，需要建立假设将缺陷折合转化为相应尺寸的椭圆进行求解。因此，在对椭圆的形状和大小统计的过程中，椭圆的短轴/长轴比值和长轴尺寸直接影响FGH96 的裂纹扩展和疲劳寿命等参数，需要予以重点关注。

通过对缺陷椭圆短轴/长轴比值进行分析统计，对于FGH96粉末材料缺陷短轴/长轴比值于（0.5～1）左右。对于缺陷椭圆短轴/长轴比值的分布，拟采用三参数指数分布对其进行拟合。具体拟合参数，如表7 所示。

表7 缺陷椭圆短轴/长轴比值拟合参数Tab.7 Defect Ellipse Short and Length Axis Ratio Fitting Parameters

通过对缺陷短轴/长轴比值分布拟合，获得了相应的拟合函数参数。针对获得的拟合函数，分别进行K-S 检验、Anderson-Darling 检验和χ2检验，并进行相应评估。检验参数，如表8 所示。缺陷长短轴密度函数和分布函数图，如图6、图7 所示。

表8 缺陷椭圆短轴/长轴比值拟合函数检验参数Tab.8 Defect Ellipse Short and Length Axis Ratio Fitting Function Test Parameters

图6 缺陷短轴/长轴比值密度函数拟合图Fig.6 Fitting Plot of Defect Short and Length Axis Ratio Density Function

图7 缺陷短轴/长轴比值分布函数拟合图Fig.7 Fitting Plot of Defect Short and Length Axis Ratio Distribution Function

对于缺陷短轴/长轴比值拟合的三参数指数分布密度函数和分布函数，如表9 所示。通过对缺陷椭圆长轴尺寸进行分析统计，对于FGH96 粉末材料缺陷长轴尺寸基本都处于（1～7）μm 左右。对于缺陷椭圆长短轴比值的分布，拟采用三参数对数正态分布对其进行拟合，具体拟合参数，如表10 所示。

表9 缺陷短轴/长轴比值拟合函数Tab.9 Defect Ellipse Short and Length Axis Ratio Fitting Function

表10 缺陷长轴拟合参数Tab.10 Defect Long Axis Fitting Parameters

通过对缺陷长轴尺寸分布拟合，获得了相应的拟合函数参数。针对获得的拟合函数，分别进行K-S 检验、Anderson-Darling检验和χ2检验，并进行相应评估，检验参数，如表11 所示。

表11 缺陷长轴尺寸拟合函数检验参数Tab.11 Defect Long Axis Dimension Fitting Function Test Parameters

缺陷长轴尺寸拟合密度函数和分布函数图，如图8、图9 所示。对于缺陷长轴尺寸拟合的三参数对数正态分布密度函数和分布函数，如表12 所示。

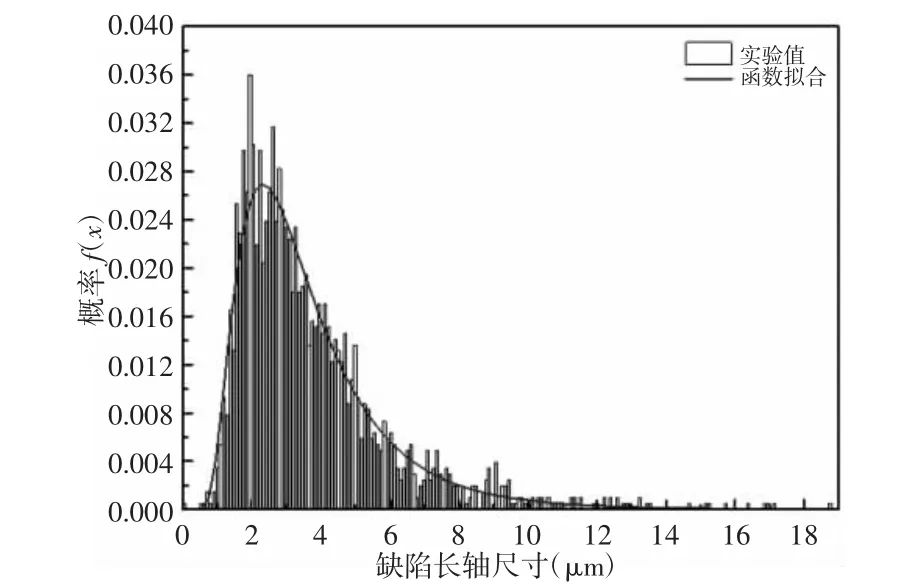
图8 缺陷长轴尺寸密度函数拟合图Fig.8 Fitting Plot of Defect Long Axis Dimension Density Function

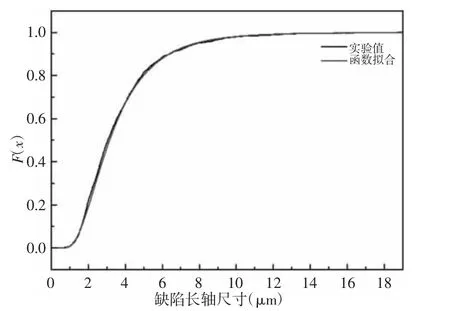
图9 缺陷长轴尺寸分布函数拟合图Fig.9 Fitting Plot of Defect Long Axis Dimension Distribution Function

表12 缺陷长轴尺寸拟合函数Tab.12 Defect Long Axis Dimension Fitting Function

4 结论

通过试验统计分析FGH96 高温合金涡轮盘初始缺陷的面积概率模型、缺陷圆度概率模型、椭圆缺陷短轴/长轴比值和长轴长度概率模型，得出以下结论：

（1）对于FGH96 粉末高温合金涡轮盘初始缺陷面积大部分都处于（1～5）μm2左右。

（2）对于不同形状的缺陷，通过圆度来对缺陷进行评估，FGH96 粉末材料缺陷圆度大部分都处于（0.3～0.7）左右。

（3）如果缺陷形状拟合为近似椭圆，针对椭圆的短轴/长轴比值和长轴尺寸进行统计分析得出椭圆短轴/长轴比值大部分都处于（0.5～1）左右，长轴尺寸基本处于（1～7）μm 左右。