考虑可制造性的拓扑优化结果的几何重构
2021-03-05张少星
杨 睿,张少星,唐 畅
(大连理工大学机械工程学院,辽宁 大连 116024)
1 引言
拓扑优化是一种根据给定负载情况和性能指标对设计域内的材料分布进行优化的结构设计方法,拓扑优化理论的发展为各种功能结构的设计带来便捷[1-2]。但是拓扑优化结果的可制造性较弱[3-4],反位移结构为例简述拓扑优化结果的特点及其给加工制造带来的问题,如图1 所示。(1)拓扑优化是基于有限元进行优化计算的设计方法,所以其轮廓为离散单元构成的不规则形状,不便于高效率的机械加工制造;(2)拓扑优化实质上提供了一种理想的材料分布图,大多得到的是结构的有限元网格信息,其结果没有具体的几何尺度与参数化信息,这导致拓扑优化结果与CAD/CAM 的数据传递受阻,无法直接用于机械加工。

图1 拓扑优化结果示意图Fig.1 Diagram of Topology Optimization Results
拓扑优化结构轮廓的不光滑和未参数化的特点导致拓扑优化结果的可制造性降低,所以需要对拓扑优化的结果进行参数化几何重构,获得一个可以满足制造要求的参数化CAD 模型,并且模型的重构不影响初始的拓扑优化结构响应。针对拓扑优化结果的几何重构问题,国内外学者从不同角度提出解决方案。付永清等人研究了柔顺机构的拓扑图的提取,提出一种基于梯度矢量流的轮廓提取方法,虽此方法可以较高精度完成拓扑图提取,但是没有解决拓扑优化结果参数化和边界光滑等问题[5]。方宗德等人利用MATLAB 完成拓扑优化结果的几何重构,用直线和圆弧逼近初始轮廓,此方法在拓扑优化结果具有复杂边界的时候,重构效果会变差并且会影响结构的初始设计性能响应[6]。GuilianYi 提出基于密度等高线法的轮廓提取算法,虽综合考虑了性能响应和轮廓光滑度,但是这种方法还需要进行形状优化才可以达到加工要求,过程较为繁琐[7]。
综上,提出一种用B 样条曲线分段描述拓扑优化结果内外边界的参数化几何重构方法,得到的拓扑优化重构模型边界光滑满足制造要求,并且可以通过调整轮廓边界B 样条曲线插值点的数目控制重构模型与拓扑优化结果的结构响应误差,达到拓扑优化结果与CAD、CAM 系统的有机结合的目的。通过算例证明该拓扑优化结果的几何重构方法可行,算法具有便捷性和通用性。
2 几何重构的流程
几何重构的整体思路为用多条B 样条曲线分段逼近拓扑优化结果的内外边界,重构的流程总体分为两大步:(1)拓扑优化结果的参数化;(2)轮廓边界的分段与重构。整体流程,如图2 所示。

图2 考虑制造性的拓扑优化结果几何重构流程Fig.2 CAD Model Reconstruction Flow Chart of Topology Optimization Results in Terms of Manufacturability
3 拓扑优化结果的参数化
3.1 拓扑优化结果二值化
在拓扑优化的计算过程中,设计变量即单元的密度值在0和1 之间变化,尽管在优化过程中引入了惩罚因子,但是拓扑优化结果仍存在中间密度单元,直观表现为拓扑优化结果中的灰度单元。考虑到拓扑优化结果的可制造性,需要对拓扑优化结果进行二值化处理,将拓扑优化结果转变为一个没有中间密度单元的模型。拓扑优化结果二值化过程的重点在于选取一个合适的阈值T,使得二值化后的单元密度值满足下面的关系:

式中:a(i,j)—拓扑优化结果中各单元的密度值;
t(i,j)—二值化后拓扑优化结果中各单元的密度值。
二值化的阈值T 选取原则为:二值化前后拓扑优化结果的单元密度和不变,该阈值选取原则的物理意义为二值化前后拓扑结构的质量不变,即二值化过程不改变结构的轻量化设计。
3.2 边界识别与参数化
由于B 样条曲线描述拓扑优化结果的内外边界,所以需要识别拓扑优化结果的边界轮廓,这是几何重构模型参数化的重要一步。首先将二值化后的矩阵遍历并提取出边界密度矩阵,然后将矩阵元素的位置转换为直角坐标保存。假如边界矩阵A 的规模为m×n,矩阵单元A(i,j)的直角坐标为(j-0.5,m-i+0.5)。如下图所示的拓扑优化局部轮廓,边界密度矩阵的规模为3×3,则第一行第一列的单元A(1,1)可以转换为直角坐标(0.5,2.5)。通过这种转换方法,可以得到拓扑优化结果的参数化模型。

图3 拓扑优化结果的参数化Fig.3 Parameterization of Topology Optimization Results
4 拓扑优化结果边界分段与重构
4.1 边界轮廓点的跟踪与排序
在对离散边界进行处理时,需要将拓扑优化结果的离散边界点按顺时针或者逆时针的顺序保存,获得闭合轮廓边界点的走向信息以便做矢量分析。链码(又称为Freeman Code)是用曲线起始点的坐标和边界点方向代码来描述曲线或边界的方法,常用的为8 向链码,每个中心像素点周围有八个像素点,分别用数字(0~7)表示,顺时针每旋转45°,链码数值加一[8]。利用链码对拓扑优化结果的轮廓边界点进行跟踪及排序,按照顺时针或者逆时针的顺序遍历所有的轮廓边界点得到轮廓边界信息的链码集合,按顺序保存边界点的坐标信息。
4.2 边界轮廓分段点识别
拓扑优化结构轮廓不规则,轮廓曲率波动较大且存在曲率突变点,所以对拓扑优化结构边界进行B 样条拟合的时候,若只采用一条B 样条曲线进行拟合,曲线不能够充分逼近初始轮廓,故而会增大重构模型的结构响应误差,所以拓扑优化结果轮廓的精确几何分段是保证重构模型结构性能响应精确实现的重要因素。由于轮廓边界离散曲率的精确性与曲率计算的支撑半径有着很大关系,考虑到拓扑轮廓边界的离散性和阶梯状的特点,并且在轮廓跟踪排序步骤中获得了结构边界的链码信息集合,故利用差分链码代替轮廓离散曲率来表述轮廓的几何信息。设轮廓边界的链码值为P1……Pi,为了避免轮廓的局部跳动带来分段点的判断失误,首先应对轮廓链码值进行加权平均处理,平均链码的计算公式如下:
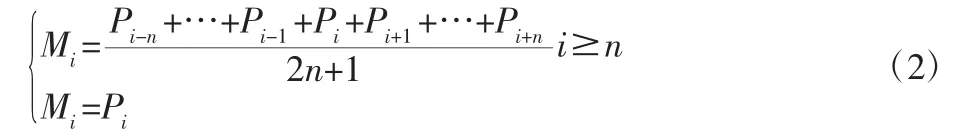
式中:n—由链码的规模大小决定,一般取值范围为3-6;Pi—边界的链码集合;Mi—平均链码集合。
差分链码可以从下面的公式计算得出:


拓扑优化结果的轮廓,其链码集合为{1 1 1 3 3 3},差分链码集合为{0 0 2 0 0},差分链码图显示在第四个点处产生脉冲,所以该段轮廓的分段点为第四个边界点,如图4 所示。
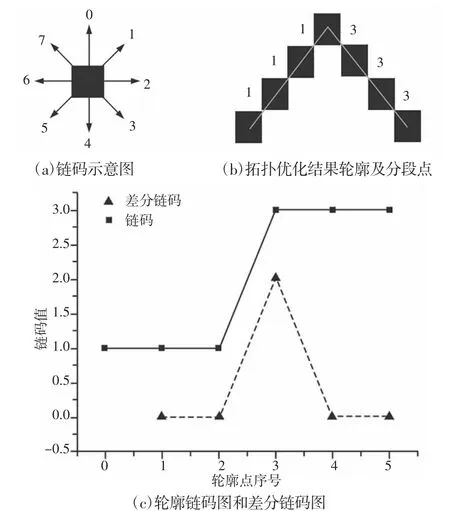
图4 轮廓边界分段点的选取过程Fig.4 Sorting Process of Boundary Points
4.3 轮廓B 样条拟合
曲线拟合的方式可以分为两类:插值和逼近。采用插值的方式时,所创建的曲线必须精确地通过所有插值点。采用逼近的方式,曲线不必精确通过所有的点,只要在误差范围内逼近即可。由于拓扑优化结果的边界点的数据规模不大,并且所有的边界点不存在“坏点”,故采用B 样条全局插值的方法重构轮廓边界[9]。
插值点的选择直接影响重构模型的几何构型和结构性能响应,为了充分逼近初始拓扑优化结果,选择均匀选取插值点策略,并且可以通过改变B 样条曲线插值点的个数控制重构模型的结构响应误差。
5 算例分析
拓扑优化的设计域,如图5(a)所示。选用材料为Q235,材料的弹性模量E=210GPa,泊松比为0.3,结构厚度为6mm,体积约束比为54%,采用4 节点矩形单元,设计目标为结构的刚度最大,柔性最小,用结构的最大位移表征结构的响应值。最终得到的拓扑结果如图5(b)所示。经计算,二值化的阈值T 为0.4381,拓扑优化结果的重构过程,如图5 所示。
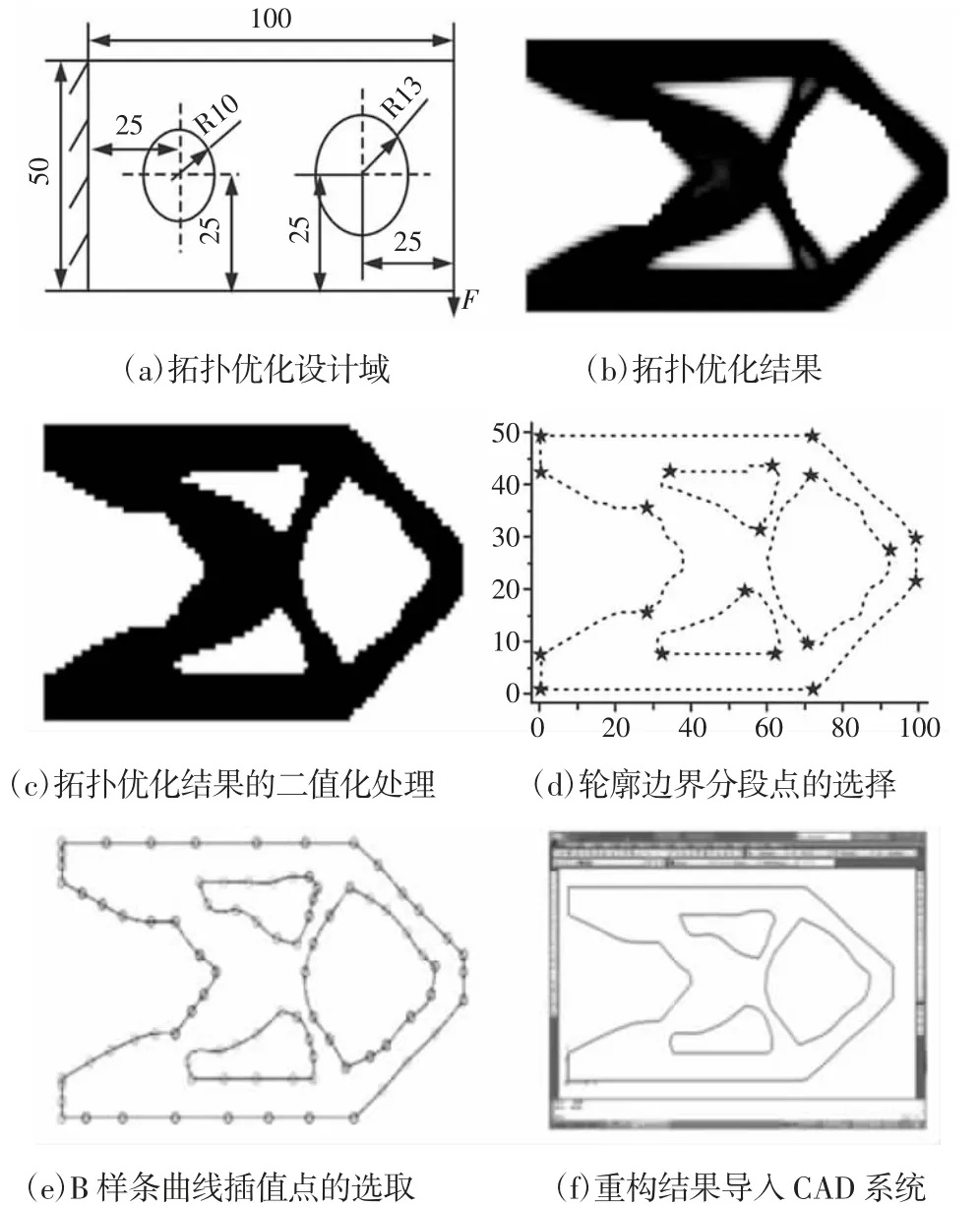
图5 拓扑优化结果几何重构的过程Fig.5 The CAD Reconstruction Process of Topology Optimization Results
将重构模型与拓扑优化初始结果导入有限元分析软件中,计算结构的最大位移变形,计算结果,如表1 所示。通过表1 可知,重构模型与拓扑优化初始设计结果的结构响应平均误差为3.86%,满足几何重构要求。结构受载时的位移分布云图,如图6所示。分析云图可知两个模型的位移分布一致。综上,几何重构模型在满足边界光滑的要求下,结构响应可以与拓扑优化结果保持一致。

表1 重构模型与拓扑优化结果的结构响应对比Tab.1 Comparison of Structural Responses Between the Reconstruction Model and the Topology Optimization Result

图6 结构受载时的位移分布云图Fig.6 Displacement Distribution Cloud Map of Structure Under Loading
6 结论
针对拓扑优化结果的可制造性问题,提出采用B 样条曲线重构拓扑优化结果的边界轮廓,使得重构模型边界光滑,满足机械制造要求,并且通过有限元分析得知,重构模型与拓扑优化结果在结构响应上基本保持一致。
上述研究仅提供一种拓扑优化结果几何重构的思路,还需进一步研究主动控制重构模型结构响应误差的方法,充实拓扑优化结果精确制造的理论。
