多间隙运动副四杆机构运动特性研究

彭京徽，周奇郑，孙 强，王 强

（海军工程大学兵器工程学院，湖北 武汉 430033）

1 引言

随着现代制造工业对机械运动精度提出越来越高的要求，精确预测机械系统的运动是机械设计的重要内容。大量的工程实践发现造成机械可靠性差的原因是存在多间隙运动副，导致构件间相互碰撞，产生的冲击使得机构磨损加重、间隙变大，偏离规划路径程度加剧。但在实际的机构装配中又无法避免间隙的产生，针对间隙引起的碰撞、振动和磨损等问题，国内外已有众多学者对含间隙运动副机构的运动特性展开了大量的理论与实验研究[1-4]。在常见的含间隙运动副的研究中，普遍基于三类接触模型，采用机械系统动力学自动分析软件ADAMS。这些研究多是对比分析单间隙和多间隙对滑块或摇杆动力学特性影响的大小，如文献[5]以平面曲柄滑块机构为例，分别考虑单个间隙和多间隙对滑块运动的影响，并对不同尺寸的间隙关节进行了分别仿真；文献[6]研究了计入移动副间隙对滑块运动特性的影响；文献[7]以空载四连杆机构为对象，分析间隙关节位置、数量及润滑对摇杆动力学响应的影响。文献[8]基于连续接触模式对轴颈与轴承进行运动学和动力学分析，利用遗传算法确定转动副的最佳间隙量。但以上研究在分析单间隙副位置对构件振荡响应曲线的影响时仅选择滑块或摇杆是不严谨的，另外不能在非单一变量下准确得到关于单间隙副位置对目标构件的影响程度的结论。

因此，在以上研究的基础上，以平行双曲柄机构为研究对象，分析了驱动间隙副和约束间隙副对目标杆动态响应，以及杆件质量对含间隙副机构的影响，同时进一步研究了双驱动下间隙副对机构动态响应的影响。

2 转动间隙副模型

2.1 转动间隙副状态

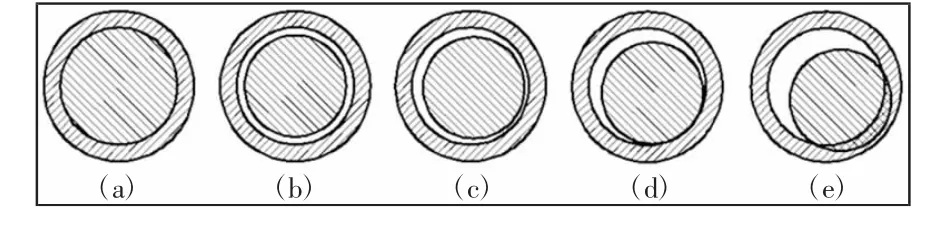
图1 转动间隙副五种状态Fig.1 Five States of Rotation Pair with Clearance

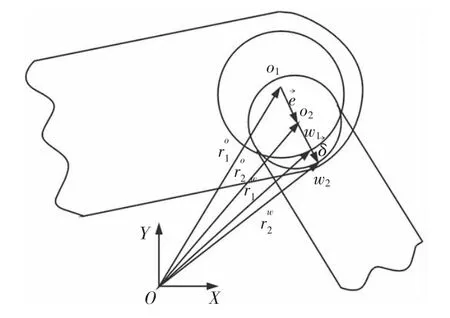
图2 旋转间隙关节模型Fig.2 Model of Rotation Joint with Clearance

2.2 接触力模型

在不考虑润滑条件下，分析含间隙转动副的冲击与碰撞常用的接触力模型[9]是Coulomb 摩擦模型[10]。

摩擦系数μ 的表达式为：

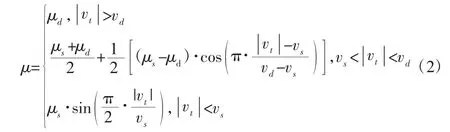
式中：vt，vs，vd—相对切向速度、静摩擦临界速度和最大动摩擦临界速度；μs、μd—动静摩擦系数。

3 间隙副对目标杆运动特性的影响

3.1 不同性质同类型间隙运动副

理想状态的平行双曲柄四杆机构，如图3 所示。杆Ⅰ与杆Ⅱ、杆Ⅱ与杆Ⅲ分别通过运动副A、运动副B 连接。杆Ⅰ上施加驱动转矩M，根据目标杆的性质可定义：杆Ⅱ是杆Ⅲ的传动杆，运动副A 是杆Ⅲ的一级驱动副，运动副B 是杆Ⅲ的二级驱动副；杆Ⅲ是杆Ⅱ的约束杆，运动副A 是杆Ⅱ的驱动副，运动副B 是杆Ⅱ的约束副。

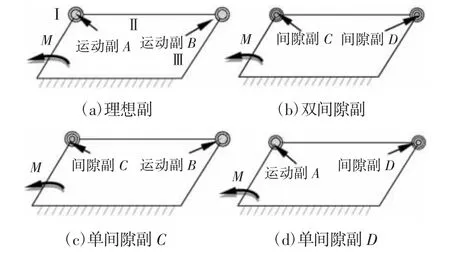
图3 平行双曲柄四杆机构转动副状态Fig.3 Status of Rotation Pair of Parallel Double Crank Four-Bar Mechanism

实际含有间隙0.5mm 运动副的无质量双曲柄四杆机构，如图3（b）所示。为了研究间隙副C、间隙副D 对目标杆运动特性影响的大小，利用ADAMS 分别对图3 四种状态进行了单驱动（30rad/s）分析。图3 四种状态模型中杆Ⅱ和杆Ⅲ对应编号，如表1 所示。

表1 各模型中杆Ⅱ和杆Ⅲ对应编号Tab.1 Corresponding Number of Rod Ⅱand Rod Ⅲin Each Model

利用ADAMS 软件在控制单一变量条件下，仿真得到杆Ⅲ的速度曲线，如图4 所示。

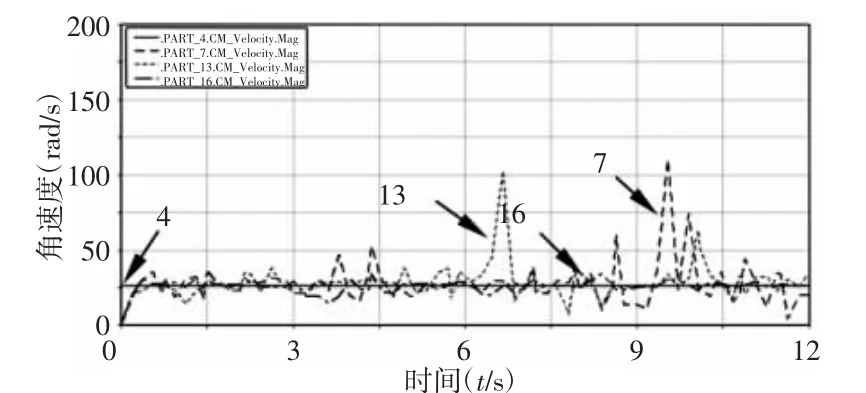
图4 无质量杆Ⅲ的速度曲线Fig.4 Velocity Curve of No-Quality Rod Ⅲ

由图4 对比四种转动副搭配状态下杆Ⅲ的速度变化曲线可知，双间隙副时杆Ⅲ（7）的速度曲线波动最大，这是因为机构减少时变约束的频率更高；单间隙副时间隙副D 对杆Ⅲ（13）速度的影响比间隙副C 对杆Ⅲ（16）大，即二级驱动间隙副D 比一级驱动间隙副C 对目标杆的影响更强烈；另外，三种状态都比无间隙时影响大，验证了间隙会增大机构的振动。

仿真得杆Ⅱ的速度曲线，分别如图5 所示。

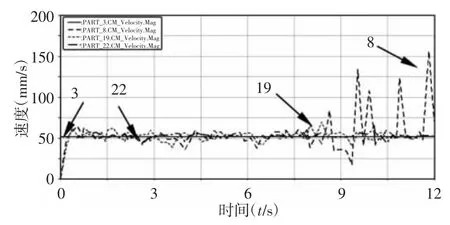
图5 无质量杆Ⅱ的速度曲线Fig.5 Velocity Curve of No-Quality Rod Ⅱ

由图5 可知，单间隙C 时杆Ⅱ（19）比单间隙D 时杆Ⅱ（22）速度曲线波动更加明显，因此，驱动间隙副比约束间隙副对目标杆Ⅱ的速度影响更大。

3.2 双驱动

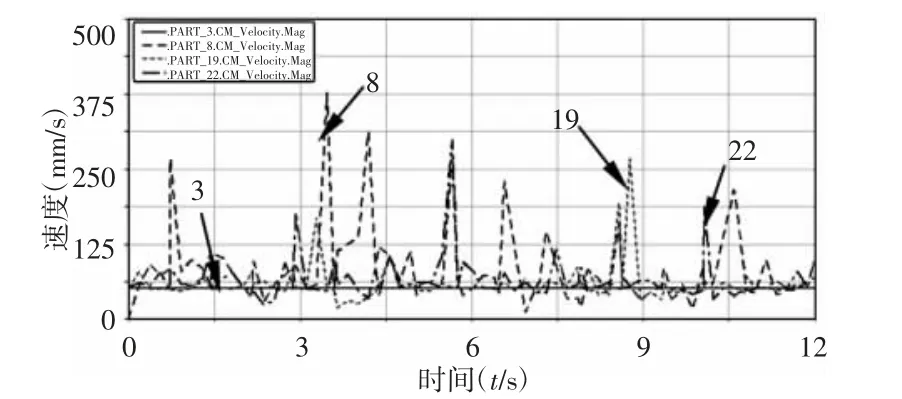
图6 双驱动下杆Ⅱ的速度曲线Fig.6 Velocity Curve of Rod Ⅱby Dual-Drive

进一步研究间隙副对杆Ⅱ的运动特性影响，对机构杆Ⅰ和杆Ⅲ施加同向双驱动（均为30rad/s）。仿真得到下杆Ⅱ的运动响应曲线，如图6 所示。由图6 并对比图5 可知，双驱动时杆Ⅱ的运动响应特性加剧，且驱动间隙副C 对目标杆Ⅱ速度的影响仍比约束间隙副D 更大。

4 其他因素间隙效应的影响

针对上述结论：二级驱动间隙副D 比一级驱动间隙副C 对目标杆Ⅲ的影响更强烈；驱动间隙副C 比约束间隙副D 对目标杆Ⅱ的速度影响更大。为了进一步论证其正确性，从转速、间隙大小和杆Ⅲ长度三个方面展开分析。

4.1 转速对间隙效应的影响

改变单驱动的转速，分别设置转速为20rad/s、40rad/s 和80rad/s，仿真得到杆Ⅲ和杆Ⅱ速度曲线分别，如图7、图8 所示。

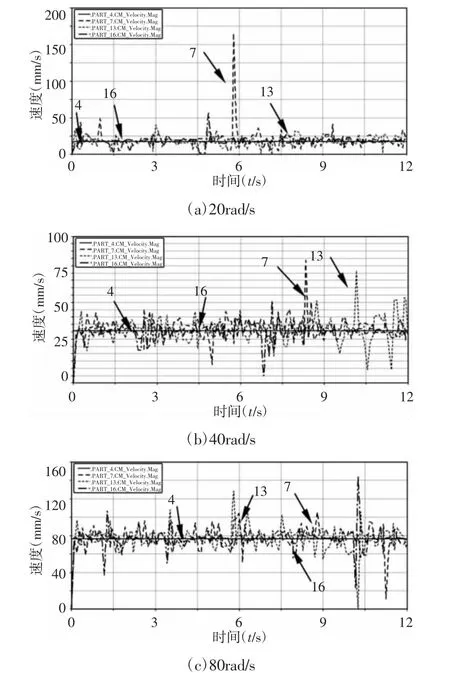
图7 不同转速下杆Ⅲ的速度响应曲线Fig.7 Velocity-Response Curves of Rod ⅢUnder Different Rotational Speed

由图7 可知，随转速增加运动响应曲线波动更剧烈，且二级驱动间隙副D 比一级驱动间隙副C 对目标杆Ⅲ的速度影响大。

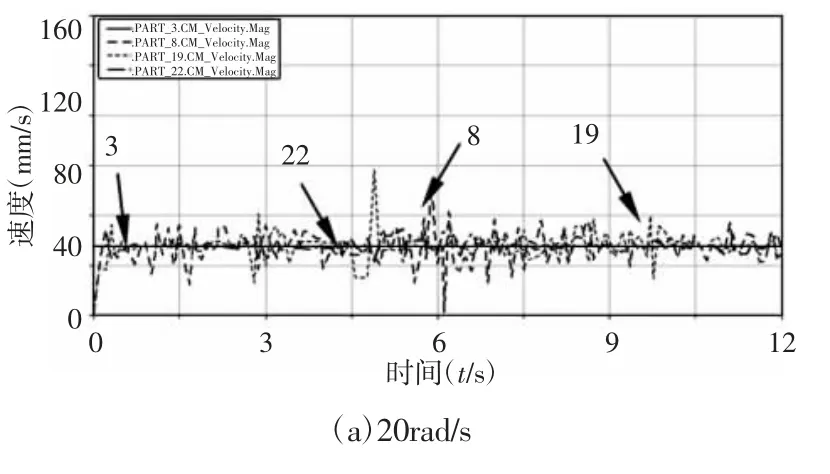
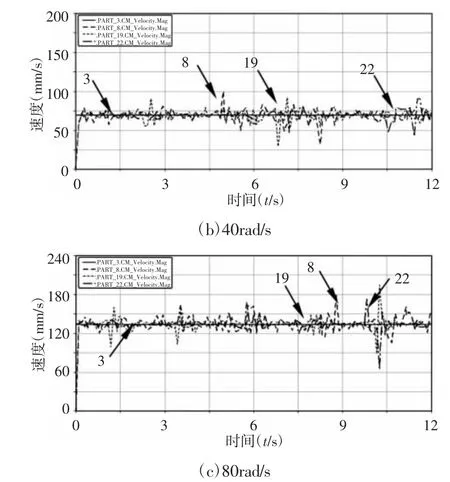
图8 不同转速下杆Ⅱ的速度响应曲线Fig.8 Velocity-Response Curves of Rod ⅡUnder Different Rotational Speed

由图8 知，运动响应曲线波动随转速增加而增大，驱动间隙副C 比约束间隙副D 对目标杆Ⅱ的作用效果更明显。

4.2 间隙大小对其作用效应的影响

为研究间隙大小对间隙副作用效应的影响，分别设定间隙大小为0.1mm、0.3mm 和0.7mm，得到仿真结果，如图9、图10 所示。

图9 不同间隙下杆Ⅲ的速度响应曲线Fig.9 Velocity-Response Curves of Rod ⅢUnder Different Clearance

由图9 可知，间隙对杆Ⅲ的运动响应的影响与间隙大小有关系，但不是成正比关系；另外间隙大小并没有改变二级驱动间隙副D 比一级驱动间隙副C 对目标杆Ⅲ的速度影响大的作用效应。由图10 知，间隙大小并没有改变驱动间隙副C 比约束间隙副D 对目标杆Ⅱ作用效果更明显的特性。

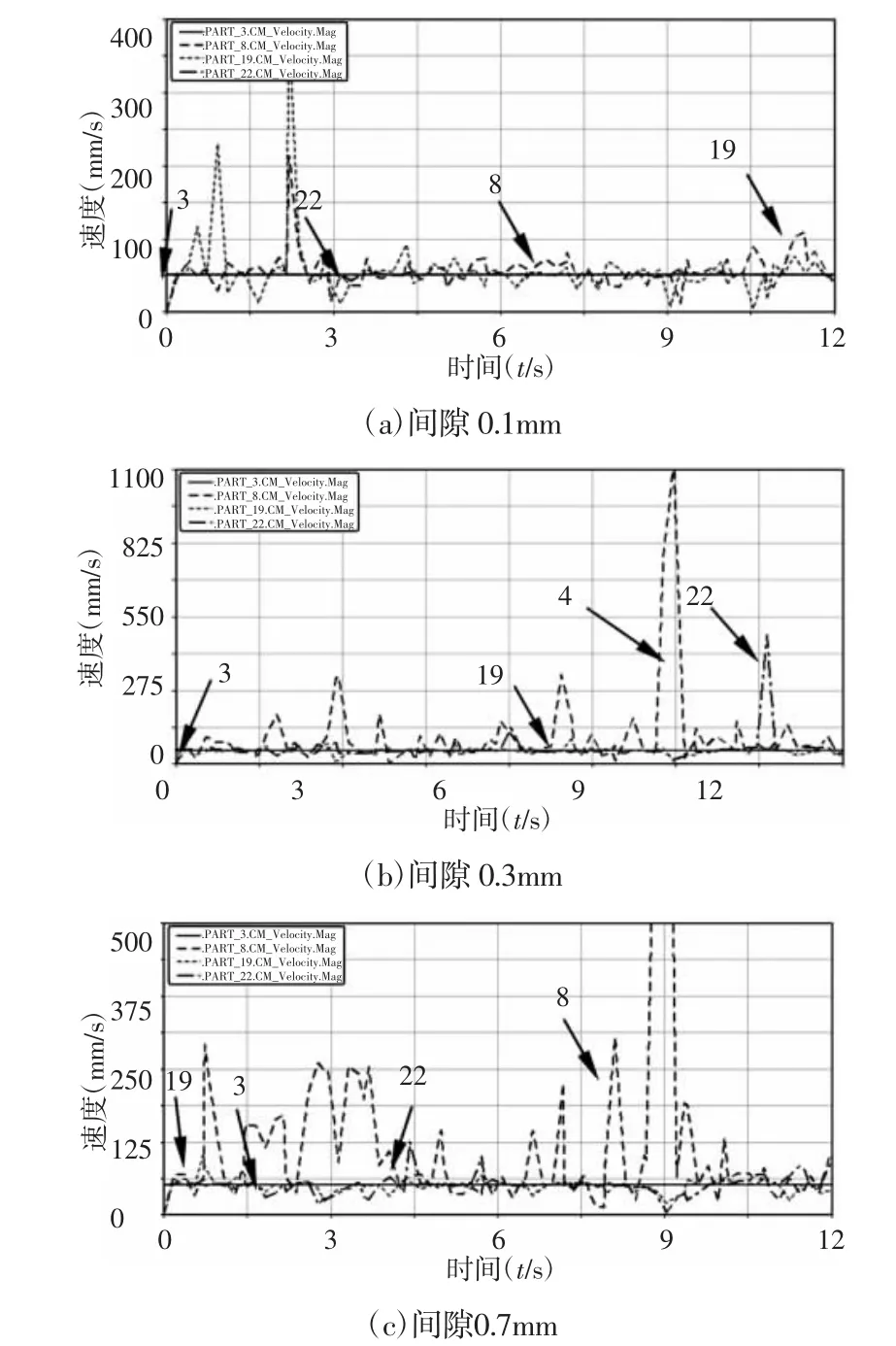
图10 不同间隙下杆Ⅱ的速度响应曲线Fig.10 Velocity-Response Curves of Rod ⅡUnder Different Clearance

4.3 杆Ⅲ长度对间隙效应的影响

为研究杆Ⅲ长度变化是否导致上述结论的改变，在保证其它三个杆长度和各运动副性质不变的基础上，展开对曲柄摇杆模型进行研究，如图11所示。各模型中杆Ⅱ和杆Ⅲ对应编号，如表2所示。

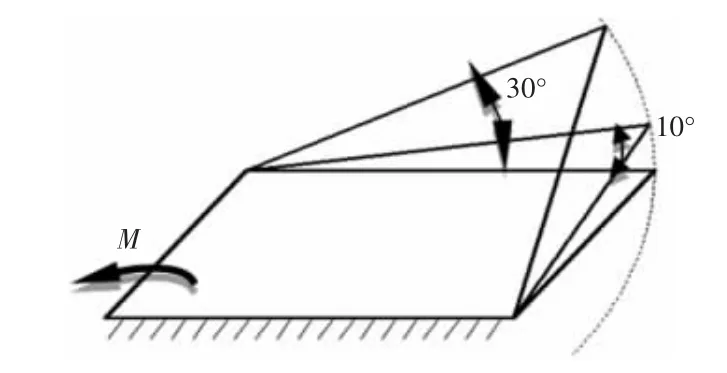
图11 杆Ⅲ长度变化模型Fig.11 Model of Rod ⅢLength Change

表2 各模型中杆Ⅱ和杆Ⅲ对应编号Tab.2 Corresponding Number of Rod Ⅱand Rod Ⅲin Each Model

得到的仿真结果，杆Ⅲ、杆Ⅱ的速度曲线，如图12、图13 所示。由图12 可知，随着杆Ⅲ长度的增加，会削弱二级驱动间隙副对杆Ⅲ响应的影响强度。由图13 可知，杆Ⅲ长度变化不改变驱动间隙副C 比约束间隙副D 对杆Ⅱ影响更大的特性。

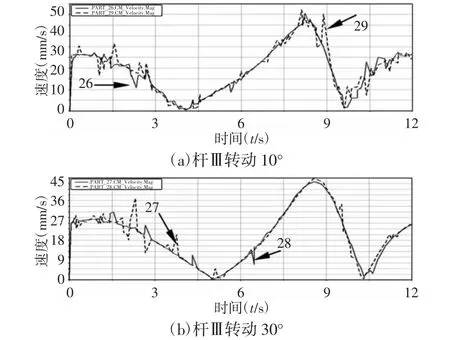
图12 杆Ⅲ的速度曲线Fig.12 Speed Curve of Rod Ⅲ

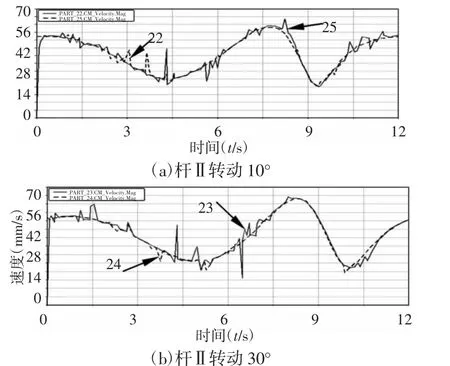
图13 杆Ⅱ的速度曲线Fig.13 Speed Curve of Rod Ⅱ

5 结论

基于四杆机构运动副的性质定义，通过ADAMS 对平行双曲柄四杆机构和变长度杆Ⅲ的曲柄摇杆机构含间隙转动副的动态特性进行了研究。结果表明：（1）对含间隙平行双曲柄四杆机构来说，二级驱动比一级驱动对目标杆Ⅲ的动态特性影响更明显。（2）驱动间隙副比约束间隙副对目标杆Ⅱ的速度影响更大。（3）随着杆Ⅲ长度增加，平行双曲柄四杆机构会变成曲柄摇杆机构，同时二级驱动间隙副对目标杆Ⅲ的影响程度会减弱。