变工况下滚动轴承静电多传感器融合监测方法研究

刘若晨，徐 成，左洪福，贝绍轶

（1.江苏理工学院汽车与交通工程学院，江苏 常州 213001；2.南京航空航天大学民航学院，江苏 南京 211106）

1 引言

滚动轴承运行过程中，轴承搭配不当、润滑油变质等因素均会导致轴承过早损坏。由于磨损的存在，即使轴承可以继续运行，轴承的性能仍在不断退化。轴承的磨损一般不易察觉，往往发现时，轴承已发生严重磨损或失效。目前，国内外对于滚动轴承的监测方法主要有振动监测、温度测量和声发射监测等[1-3]。静电监测技术是一种新型监测手段，可应用于对滚动轴承的监测，当滚动轴承运行时，由于摩擦起电、表面荷电以及磨粒荷电等因素，会使滚动轴承在磨损的过程中产生大量的静电[4-7]。静电监测基于静电感应原理[8]，产生的静电与探极感应面接触时，将会产生相反电位的电量，并将电子重新分配，从而使传感器探极内增加的电量得到平衡，通过信号调节产生相应的输出信号，如图1 所示。针对静电监测技术，国内涌现了一批学者对此技术展开了研究，其中左洪福团队率先开展了对发动机气路、润滑油路和磨损区域三个方向的研究[9-14]。结果表明静电传感器在故障监测上效果显著。然而，当被测量越来越多、越来越复杂时，往往单一的静电传感器不能实现精确有效的监测。为了加强静电监测方法对滚动轴承磨损状况的监测能力，采用多个静电传感器对滚动轴承进行监测，并基于多传感器信息融合技术[15]，采用时域算法和复杂度度量算法对特征参数进行提取，提出移动窗局部离群因子（MWLOF）检测算法，并根据滚动轴承静电综合监测平台对滚动轴承进行变工况监测试验，从而验证了所提算法在静电综合监测中的有效性。

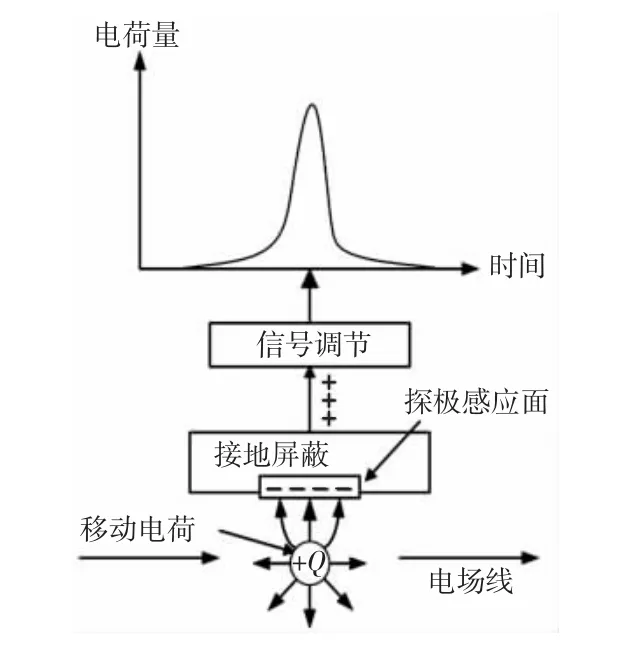
图1 磨损区域静电感应原理Fig.1 Principle of Electrostatic Induction in Wear Area

2 多源信息融合算法

2.1 特征提取

特征参数的提取是故障诊断的关键。常用的提取方法有时域特征提取和目前广泛重视的复杂度度量方法。传统的时域特征的参数指标包括平均值、均方根值、标准偏差、峰值、偏度和峭度，如表1 所示。时域指标的计算十分简便，可以快速得到，然而时域指标不能及时地发现轴承早期性能退化反应，为了弥补这一不足，引入了复杂度度量参数，如样本熵、近似熵等。复杂度度量是一种基于非线性信号的定量描述方法。该方法能够避免工况的干扰，提高静电监测早期的故障检测能力。

表1 传统的时域特征的参数指标Tab.1 Parameters of Traditional Time Domain Characteristics

2.2 MWLOF 算法原理

2.2.1 局部离群因子

局部离群因子（LOF）可用于离群点检测，是一种基于密度的检测算法[16]。为了实现离群点检测的目的，赋予每一个数据对象一个局部离群因子，从而考察每一个数据对象与其周围近邻相比的孤立程度。给定一个数据集X=［x1，x2，…，xN］T，计算出每个样本xa的k 个近邻点，所得集合用knn（xa）表示，表达式如式（1）所示。

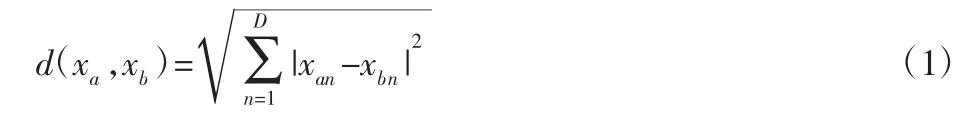
按距离从小到大将样本xa排列，第k 个近邻点到xa的距离记作k-dis tan ce（xa），可表示为d（xa，xb）的第k 个最小的值，定义xa相对xb的可达距离如下：

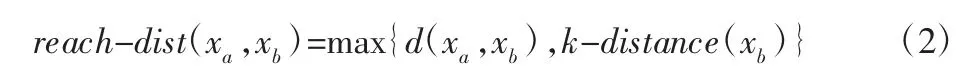
由式（2）可以看出xa相对xb的可达距离是xa到xb的实际距离和xb邻域最大展开半径之间较大的一个值。需要注意的是，kdistance（xa）不总是等于k-distance（xb），即reach-dist（xa，xb）≠reach-dist（xb，xa）。

xa的局部可达密度的表达式如下：

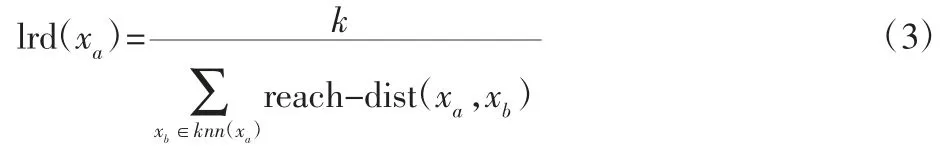
由式（3）计算出xa及其所有近邻点的局部可达密度，通过所得到的结果求出相应xa的局部离群因子值，表达式如下：

由LOF 的定义可知，它是一种基于密度的方法，该方法可对数据对象进行量化，给定其相对应的量化指标，并通过量化指标准确的找到相应的离群点，根据lof（xa）的值来判断是否是离群点。当lof（xa）的值越大，xa是离群点的概率越大。当lof（xa）远小于1 时，xa的密度大于其邻域内点的平均密度，此时xa是正常点的可能性较大。当lof（xa）趋近于1 时，xa邻域点的平均密度近似等于xa的密度，此时xa是离群点的概率非常小。当lof（xa）显著大于1 时，此时xa则为离群点。

2.2.2 在线模型更新

在监测过程中，当静电信号出现慢漂移和受到扰动时，离线建立的稳态模型会将正常的变化视为故障来处理，因此考虑将移动窗策略加入LOF 算法中，从而使模型具有自我更新的能力，适应监控过程中的变化，具体的方法和操作如下。

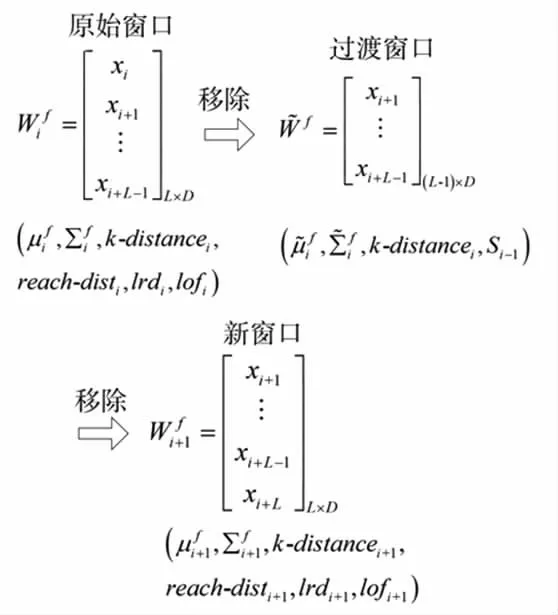
图2 移动窗口中的在线模型更新Fig.2 Online Model Update in the Moving Window

主要的步骤有两步，第一步是移除最老的样本，第二步是添加新样本。在执行第一步移除最老的样本后，相应的均值，方差和协方差的变化如下所示：

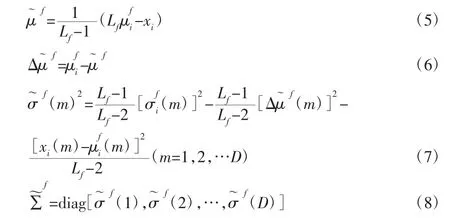
式中：D—样本的维度。

式中：xj∈Si-1。在移除最老样本，判定新的样本xi+L为正常样本后，将它添加到窗口中，然后进行模型更新。添加新的样本后，均值、方差和协方差表达式如下：

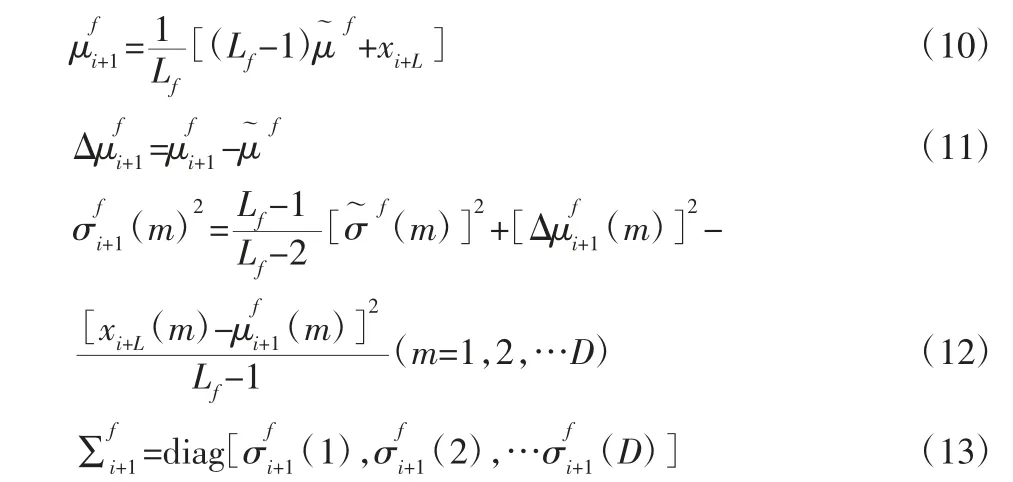
在窗口中添加新样本xi+L后，当新样本xi+L距离目标样本更近时，集合中样本的k-distance 值将更新为：

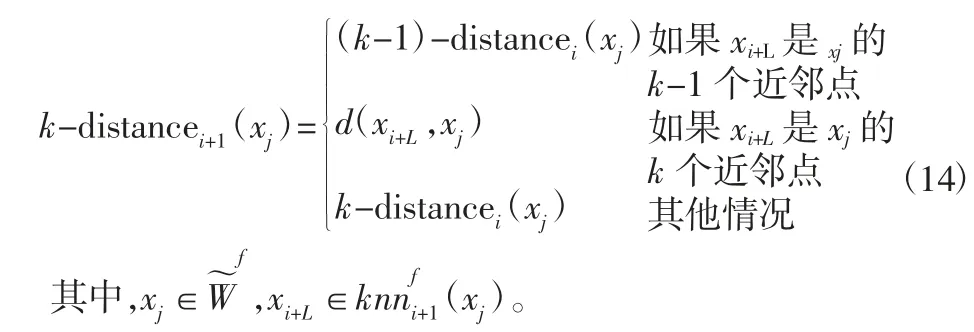
由可达距离的定义，可以得出xj相对xq的可达距离不一定会随着其近邻点xq的k-distance（xq）值改变而发生变化，故kdistance（xq）在改变之后有可能会大于d（xj，xq），也有可能改变后仍然小于d（xj，xq），结果具有不确定性。因此，需要对Si-1中样本的可达距离重新计算，表达式如下：

局部离群因子的值为：

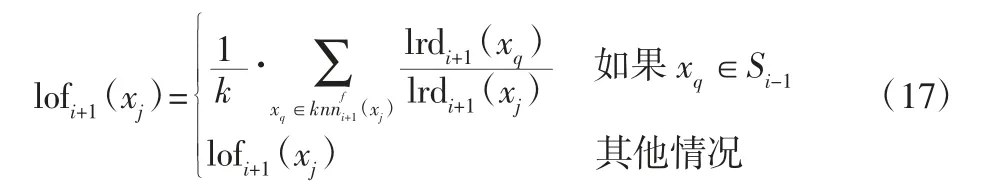
通过以上对LOF 的性能分析可知，如果lofi（xi+L）≤1，此时的局部区域的样本密度是十分高的，这对估计窗口的概率密度函数有很大帮助，故可以不再重新计算窗口Wi+1的控制限，但需要注意的是，此时窗口仍需要向前移动，并且随着xi+L的引入，邻域关系也需要更新。这是因为新样本的引入能够实时监控设备当前的运行状态，当判定新样本为正常样本时，就必须进行移除和添加两个步骤。

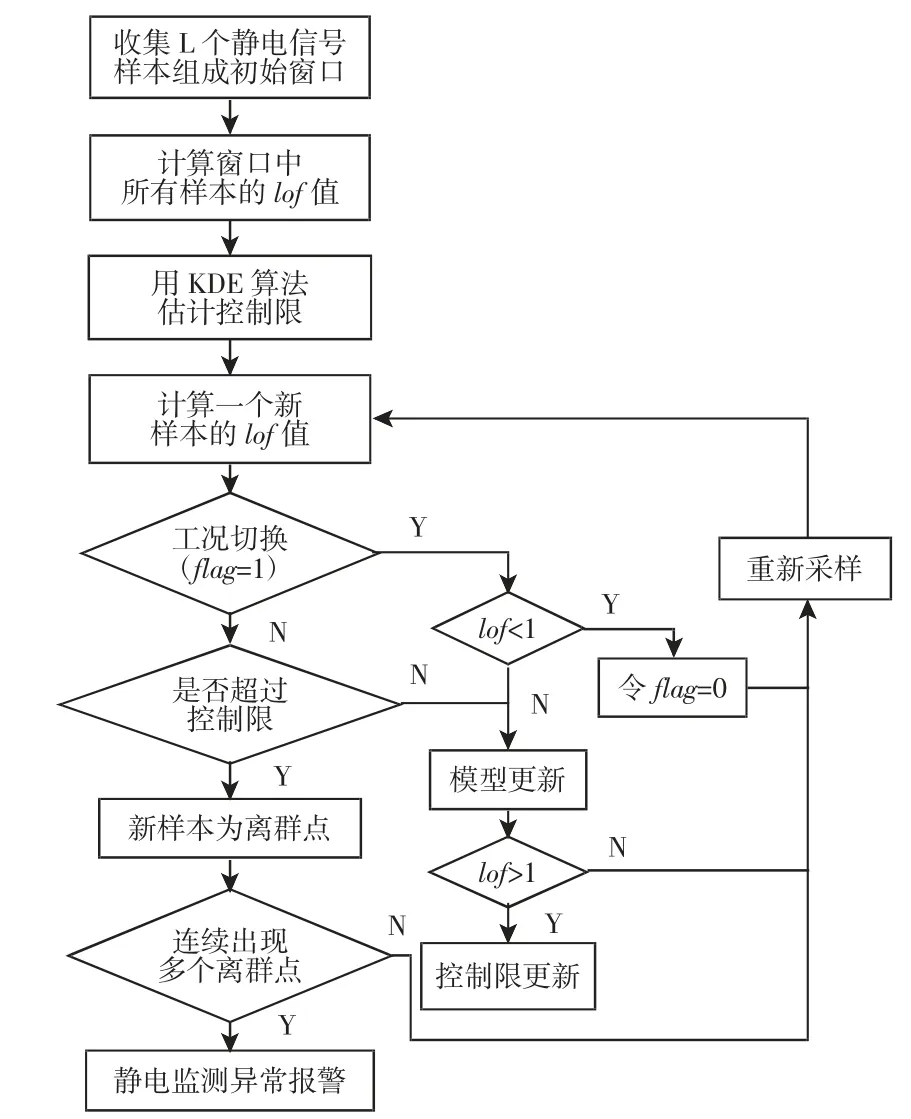
图3 静电监测流程Fig.3 Electrostatic Monitoring Process

3 静电多传感器信息融合

3.1 静电多传感器信号初始转化

mean—其均值；

bi—Bj的一个变量；

σ—其标准差。

通过计算得到新样本集X=｛X1，X2，…，Xd｝=｛x1，x2，…，xD｝，其中，xi∈RN（N=1，2，…D），Xj∈RN×m（j=1，2，…，d），D 为新样本集X 的变量总数，等于提取的特征参数个数m 与静电信号输出端口总数d 相乘，即D=m×d，最后将新样本集X 应用于静电多传感器信息融合。

3.2 多工况时变下静电监测流程

对具有时变特性的静电信号进行监控，可通过引入移动窗策略来完成，然而当运行工况发生正常的切换时，仅通过算法分析可能会将工况的切换误认为故障来处理。为避免这样的问题，在工况发生切换时，可强制的将所有新样本认定为正常样本，从而促使模型能够准确的监测新的工况。但是，当故障发生在“盲更新”期间时，这会导致模型中出现故障样本，从而使监测无效。因此，对LOF 来说，当lofi（xnew）≤1 这种情况出现时，即可结束“盲更新”，结合MWLOF 算法，形成的静电监测流程，如图3 所示。

4 实验验证

4.1 滚动轴承监测实验平台

滚动轴承监测实验平台，如图4 所示。该实验平台通过4 个磨损区域静电传感器同时监测滚动轴承的磨损状况。

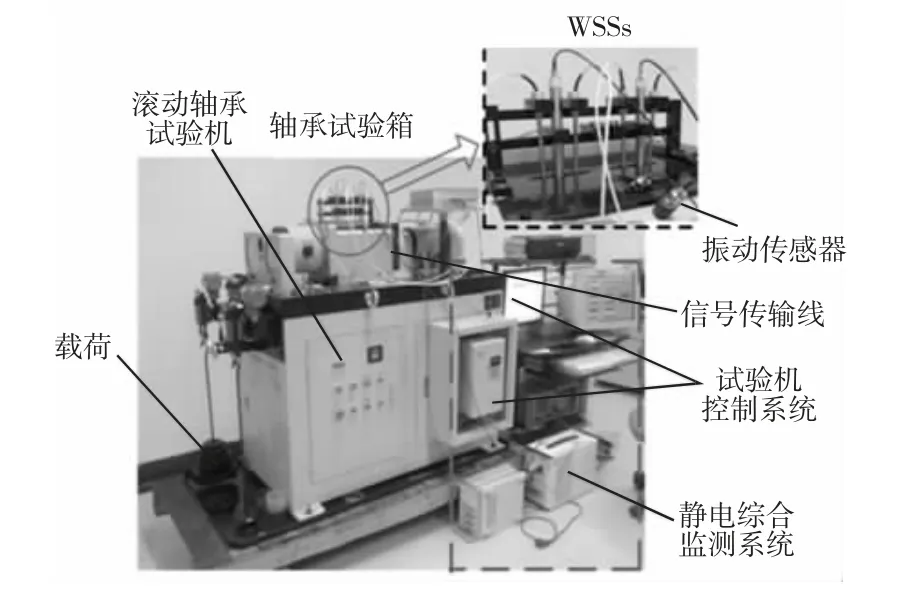
图4 滚动轴承静电综合监测实验平台Fig.4 Experimental Platform for Comprehensive Electrostatic Monitoring of Rolling Bearing

为了避免实验中设备发生故障，平台上还安装了振动和温度传感器，用来监测实验过程中的振动和温度信号。实验过程中，在轴承运行至稳定状态时，调整轴承的转速与径向载荷，在多工况下对滚动轴承进行静电在线监测，得到相对应的静电信号。

4.2 实验结果

通过在同一工况下对滚动轴承进行两次实验来验证所提算法的准确性，实验1 的初始径向载荷和初始转速分别为20kN 和2000r/min，而实验2 的初始径向载荷和初始转速分别为25kN 和2500r/min，如表2 所示。

表2 实验初始参数Tab.2 Experimental Initial Parameters

在滚动轴承运行至稳定状态时，将径向载荷和转速分别调整至30kN 和3000r/min，在该工况下继续运行滚动轴承，直至失效。采用考虑工况变化的MWLOF 算法结果，如图5、图6 所示。图中的（a）表示滚动轴承运行时，在全寿命周期中，所监测到的lof 值和相应时刻所得到的阈值。而（b）-（e）则表示为阈值的变化趋势。

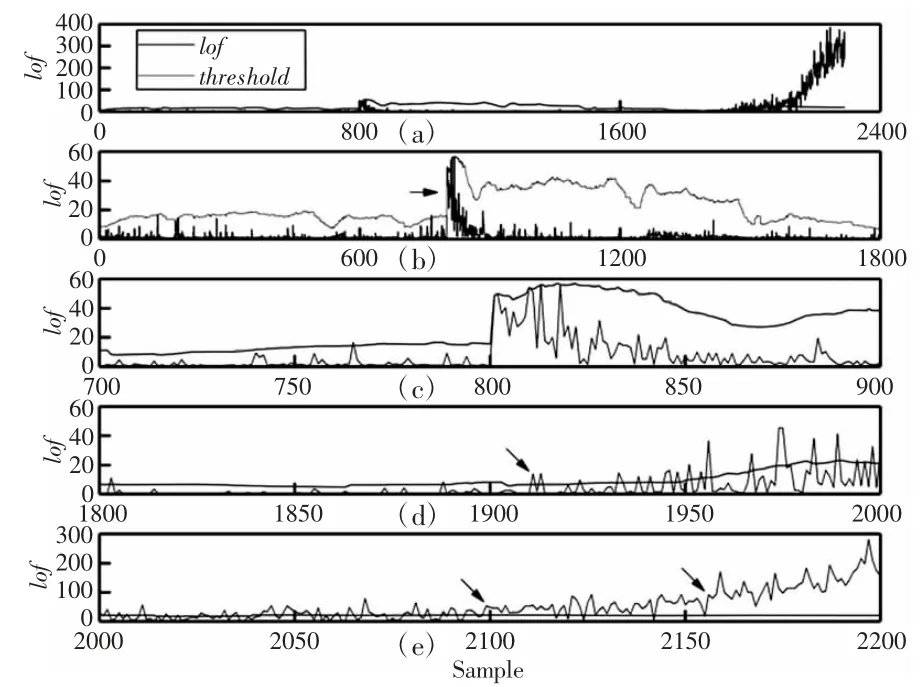
图5 实验一考虑工况变化的MWLOF 算法监测结果Fig.5 Experiment 1 Monitoring Results of the MWLOF Algorithm Considering the Change of Working Conditions

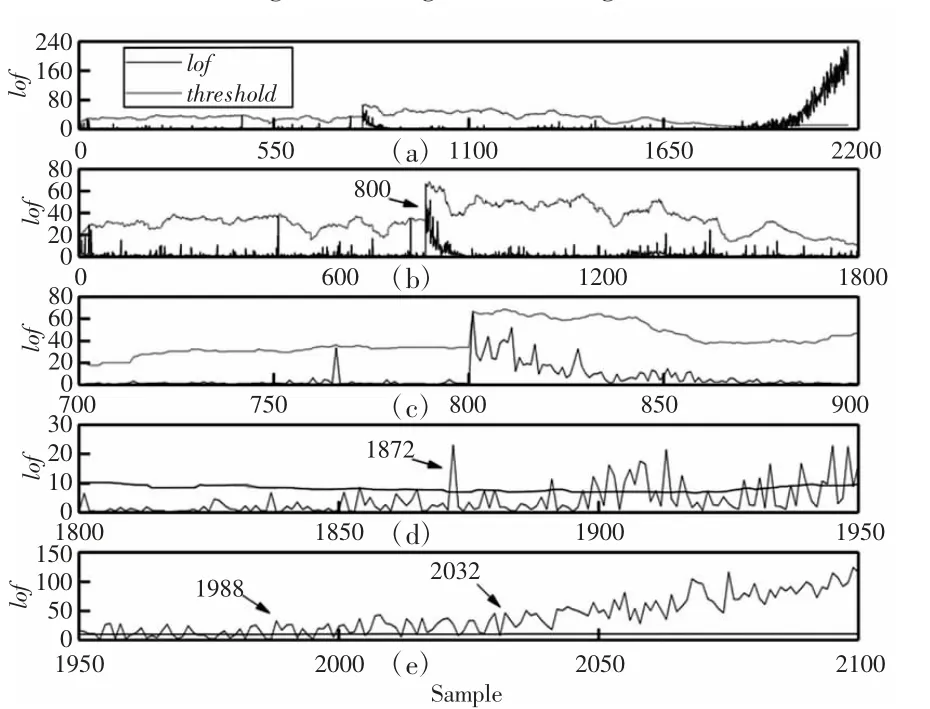
图6 实验二考虑工况变化的MWLOF 算法监测结果Fig.6 Experiment 2 Monitoring Results of the MWLOF Algorithm Considering the Change of Working Conditions

实验中滚动轴承的状态变化可分为：早期性能退化状态、较严重的磨损状态以及性能完全失效状态。可见，通过考虑工况切换的MWLOF 算法监测即可反映滚动轴承全寿命周期状态变化。为了进一步说明考虑工况切换的MWLOF 算法的监测作用更加显著，对滚动轴承进行不考虑工况变化监测进行对比，监测结果，如图7、图8 所示。通过对比可得，在不考虑工况变化的情况下，当样本数到达800 时，异常值开始增多，而通过观察，轴承此时并未发生故障，说明监测结果是不准确的。

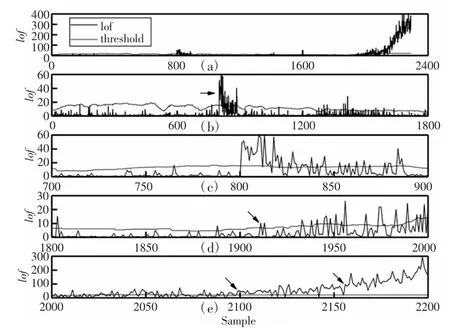
图7 实验一不考虑工况变化的MWLOF 算法监测结果Fig.7 Experiment 1 Monitoring Results of the MWLOF Algorithm without Considering the Change of Working Conditions

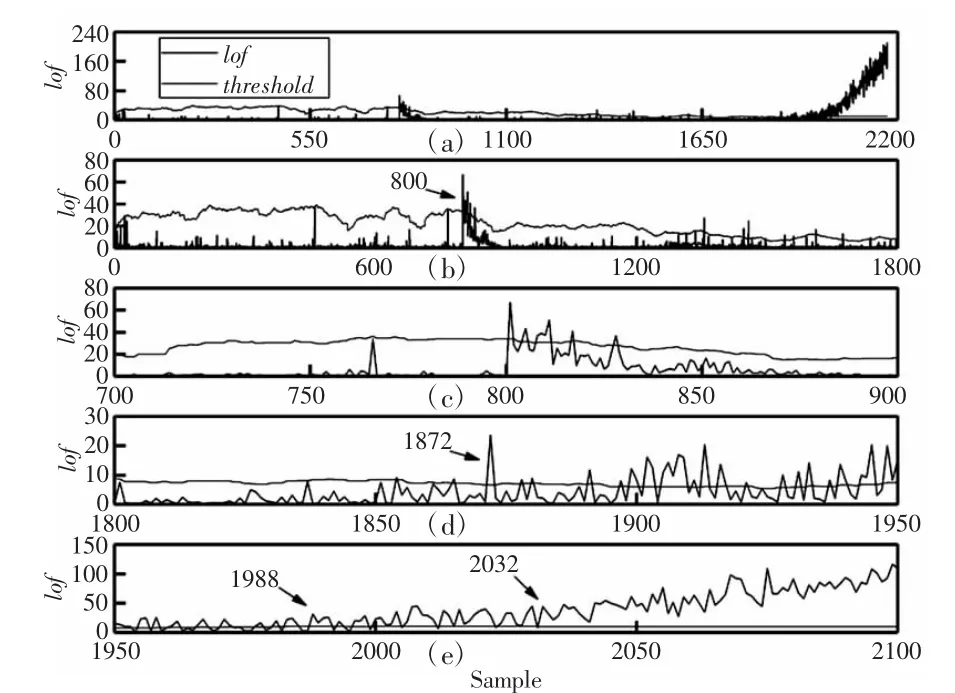
图8 实验二不考虑工况变化的MWLOF 算法监测结果Fig.8 Experiment 2 Monitoring Results of the MWLOF Algorithm without Considering the Change of Working Conditions

接着，再对滚动轴承进行不采用移动窗策略的LOF 算法监测，监测结果，如图9、图10 所示。通过图9、图10 可知，在不采用移动窗策略的LOF 算法监测的情况下，当样本到达800 时，异常值也明显增多，连续出现多个超过阈值的值，而此时轴承也并未发生故障，可见其结果也是不准确的。

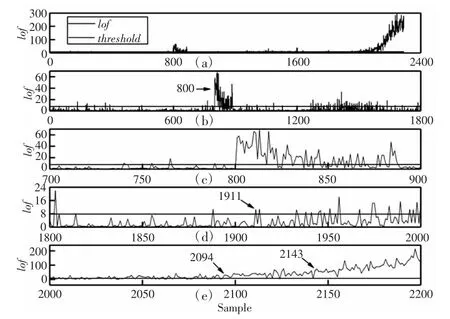
图9 实验一不采用移动窗策略的LOF 算法监测结果Fig.9 Experiment 1 LOF Algorithm Monitoring Results without Moving Window Strategy

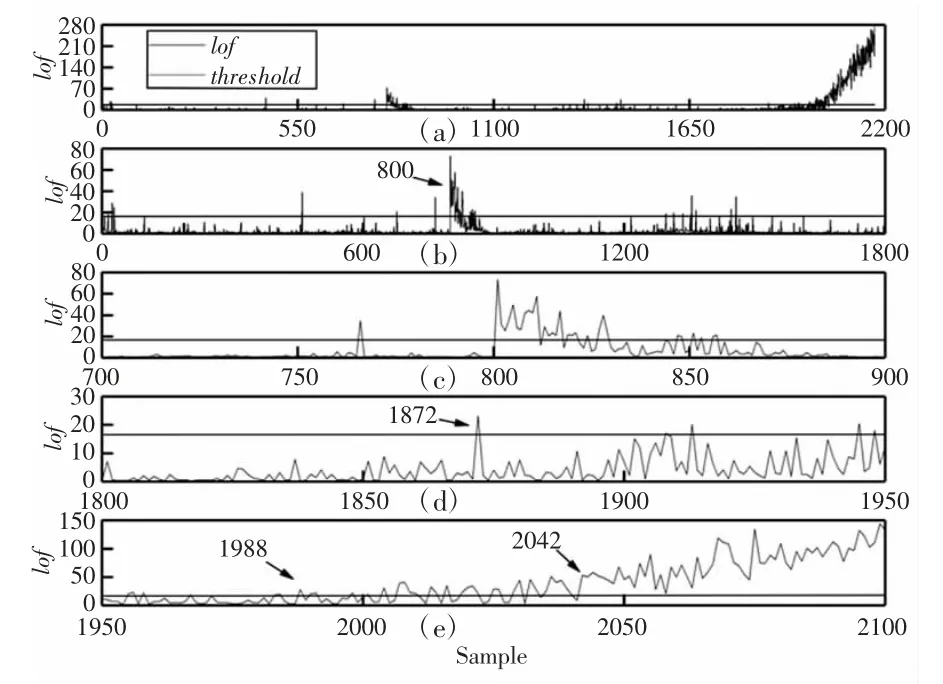
图10 实验二不采用移动窗策略的LOF 算法监测结果Fig.10 Experiment 2 LOF Algorithm Monitoring Results without Moving Window Strategy

5 结论

（1）基于静电监测原理，通过多静电传感器对滚动轴承进行同时监测，并通过时域特征和复杂度度量的方法提取特征参数。为了使静电综合监测的信息能够融合，采用离群点故障检测方法，从而得到相应的lof 值和控制限阈值。（2）滚动轴承全寿命周期状态变化可通过考虑工况切换的MWLOF 算法监测来反映，该算法监测能够更加有效的提高对滚动轴承的静电监测能力。