转子压缩机滚动活塞角速度的计算方法比较

2021-03-05王晓波

机械设计与制造 2021年2期

梁鹏，郭峰，王晓波

（1.青岛理工大学机械与汽车工程学院，山东青岛 266520；2.中国科学院兰州化学物理研究所固体润滑国家重点实验室，甘肃兰州 730000）

1 引言

压缩机可分为容积式和速度式，容积式压缩机包括转子压缩机、活塞式压缩机[1]、涡旋式压缩机[2]及螺杆式压缩机等，而其中的转子滚动式压缩机以其工作平稳、结构简单、重量轻等诸多优良品质得到了广泛应用，如家用空调、电冰箱及小型商用制冷设备。绝大部分2.2kW（3P）以下的家用空调均采用转子式压缩机。转子压缩机内的滚动活塞是实现其工作原理的最重要部件之一，滚动活塞的运动由两部分（随主轴绕气缸中心的公转和绕主轴中心的自转）组成，其复杂的运动状态很难进行实验测量，故对活塞角速度的研究大多依靠理论计算。活塞角速度的精确计算对于研究各部件的相对运动速率、受力分析、压缩机摩擦功耗及偏心轮轴平衡等都非常重要。

目前，很多学者提出了各自的方法来计算滚动活塞的角速度，如精确迭代法，简化解析式法和平均值法。精确迭代法虽然计算准确，但计算过程复杂；简化解析式法和平均值法计算简单，但精确度稍差。文献[3]分别利用迭代法求解滚动活塞的运动微分方程，从而计算活塞角速度并利用角速度值求解压缩机的摩擦损失。文献[4]通过迭代法求解纳米冷冻机油润滑条件下压缩机活塞的角速度，研究冷冻机油对压缩机摩擦功耗的影响。文献[5]假设滚动活塞处于稳定工作状态，并将滚动活塞视为匀速转动的自由体，推导出活塞角速度的简化解析式。文献[6]利用此简化解析式计算活塞角速度，继而对CO2跨临界循环膨胀机的动力学特性进行计算，为膨胀机的设计提供了依据。有些学者通过更进一步的条件简化，得到活塞角速度的平均值公式。文献[7-8]认为活塞处于近似稳定状态，其角速度为常量，通过推导得到活塞角速度的平均值公式，并根据算例中的参数计算某型号压缩机的活塞角速度值。文献[9]通过简化条件推导出活塞角速度的另一种平均值公式，并利用此公式计算家用冰箱旋转压缩机的动力学参数。转子压缩机活塞角速度计算的精确度对于压缩机动力学研究的准确性非常关键，近年来提出的简化解析式法和平均值法虽然具有计算简便的特点，但是其精确程度有待讨论，通过文献检索并未发现有文献关于两种方法的精度对比研究。故在之前的研究基础上[10]，利用三种方法（精确迭代法，简化解析式法和平均值法）分别计算滚动活塞角速度，并研究润滑油粘度、主轴转速、滚动活塞与气缸端盖间隙、滚动活塞与偏心轮间隙等参数对活塞角速度的影响。

2 活塞角速度的三种计算方法

滑片是与滚动活塞直接接触的零部件，首先对滑片的受力进行简单分析。滑片运动中受到较多力的影响，如滚动活塞与滑片顶端之间的接触力Fn和摩擦力Ft，滑片槽与滑片之间的接触力FR1、FR2以及摩擦力FRt1、FRt2等。在滑片所受外力中，Fn是滑片与滚动活塞相互作用的一个重要作用力，其计算公式为：

式中：μs—滑片槽与滑片间的摩擦系数；Fh—滑片伸到气缸内的部分受到的压差；l0—滑片的径向长度；Bv—滑片的厚度。

滚动活塞在工作过程中有两个运动：活塞随着偏心主轴绕气缸中心的公转以及活塞绕着偏心主轴轴心的自转。根据动力学方程可得活塞的运动微分方程[4]：

式中：ωp—滚动活塞的角速度；Ipo—滚动活塞的转动惯量；Ma、Mb、Mc—活塞与气缸内壁、气缸端盖、偏心主轴间的摩擦力矩。式子（2）可以采用改进欧拉法迭代求解。

如果假设滚动活塞处于稳定工作状态，即将其视为匀速转动的自由体，则可求解出滚动活塞角速度的简化解析式为[6]：

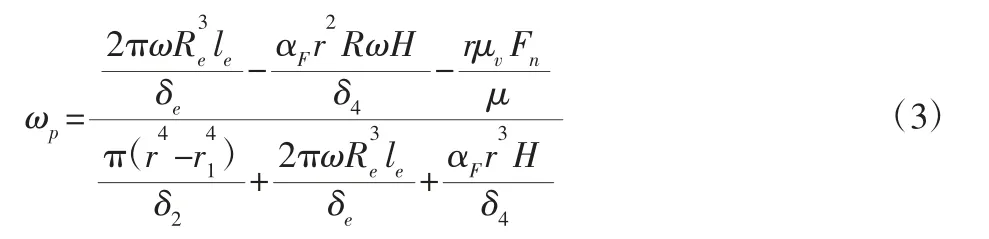
式中：r、r1—滚动活塞的外径和内径；μv—滑片端部与滚动活塞间的摩擦系数；Re—偏心轮半径；le—偏心轮长度；αF—油膜弧角；ω—偏心主轴的角速度；δ4—油膜的平均厚度。

如果假设滚动活塞的角速度为一个恒定值，则活塞的角速度平均值公式为[7]：

式中：R—气缸内径；μ—润滑油的动力粘度；δe—滚动活塞与偏心主轴的间隙；δ2—滚动活塞与气缸端盖的间隙。

3 活塞角速度计算方法的准确性比较

利用MATLAB 软件分别编写了精确迭代法（式（2））、简化解析式法（式（3））及平均值法（式（4））三种方法的计算程序，利用三种方法计算某型号转子压缩机滚动活塞的角速度，并研究润滑油粘度μ、主轴转速n、滚动活塞与气缸端盖间隙δ2、滚动活塞与偏心主轴间隙δe对活塞角速度的影响。仿真过程中，该型号转子压缩机的结构参数可参考文献[11]。首先，需要对迭代法程序的精确性进行验证，结合文献[12]，将迭代法程序计算的活塞角速度与文献[12]中的结果进行比较，如图1 所示。从图中可以看出，迭代法计算结果与文献[12]的计算结果一致性较好，证明迭代法程序计算精准，可用于比较和评价其他两种方法（简化解析式法和平均值法）的准确性。

图1 迭代法精确性的验证Fig.1 Verification of Accuracy of Iterative Method

不同工况下利用三种方法（精确迭代法，简化解析式法和平均值法）计算得到的滚动活塞角速度，图中同一种颜色曲线代表利用同一种方法得到的结果，而不同的线型代表不同的工况，如图2～图5 所示。润滑油粘度μ 不同时，三种方法得到的滚动活塞角速度值，如图2 所示。从图中可以看出：（1）随着润滑油粘度的升高，迭代法计算出的滚动活塞角速度ωp值是增大的，且ωp随着主轴转角θ 的变化趋势类似于弦函数；（2）利用简化法计算得到的滚动活塞角速度ωp整体变化趋势与迭代法得到的ωp近似相同，但数值上却差别较大且简化法计算值偏小，平均法得到的滚动活塞角速度ωp仅仅是一个恒定值且比迭代法计算值大很多；（3）简化法得到的ωp计算结果在最大值及附近区域随润滑油粘度增大而减小，但在其他区域ωp却随润滑油粘度增大而增大，这与迭代法计算的ωp变化趋势一致；（4）润滑油粘度对平均法计算的ωp值影响很小，但平均法的ωp也是随着润滑油粘度增大而略微增大，此变化趋势也与迭代法计算的ωp一致。

图2 不同润滑油粘度μ 时活塞角速度的计算结果Fig.2 Calculation Results of Angular Velocity of Piston with Different Oil Viscosity（μ）

利用三种方法仿真计算主轴转速n 不同时滚动活塞角速度ωp，如图3 所示。可以发现：不论采用何种方法，计算得到的活塞角速度ωp都随着主轴转速n 的增大而明显提高；虽然简化法得到的ωp值变化趋势与迭代法的ωp趋势一致，但两者之间差距仍然明显，且差距随转速n 的增大而越发显著；平均法计算的ωp仍然对主轴转角θ 的变化不敏感，且平均法与迭代法的ωp值差距随主轴转速的增大而增大。

图3 不同主轴转速n 时活塞角速度的计算结果Fig.3 Calculation Results of Angular Velocity of Piston with Different Speed（n）

图4 不同δ2（滚动活塞与气缸端盖的间隙）时活塞角速度的计算结果Fig.4 Calculation Results of Angular Velocity of Piston with Different Clearance（δ2）Between Rolling Piston and Cylinder End Cap

图5 不同δe（滚动活塞与偏心主轴的间隙）时活塞角速度的计算结果Fig.5 Calculation Results of Angular Velocity of Piston with Different Clearance（δe）Between Rolling Piston and Eccentric Shaft

压缩机内部很多零件之间存有间隙，这些间隙的大小会影响摩擦力，继而影响滚动活塞的角速度。不同δ2（滚动活塞与气缸端盖的间隙）和δe（滚动活塞与偏心主轴的间隙）时滚动活塞角速度的计算结果，如图4、图5 所示。从两图可以看出：（1）随着δ2的增大，迭代法和平均法计算得到的活塞角速度ωp也是增大的，但δ2值越大其对活塞角速度ωp的影响越弱，这从δ2=10μm 和δ2=20μm 时ωp 的曲线非常逼近可以看出；（2）简化法计算得到的ωp在最大值及附近区域随着间隙δ2增大而增大，但在其他区域变化趋势却相反；（3）虽然简化法得到的ωp与迭代法得到的ωp变化趋势相近，但其数值上的差距随着间隙δ2的增大而越来越明显；（4）不论采用何种计算方法，随着间隙δe的增大，活塞角速度ωp是减小的；（5）当δe=0.5μm 和δe=12.5μm 时，简化法与迭代法的计算结果差别较大，而当δe=2.5μm 时，两种方法的计算结果差别却较小，这说明存在最优间隙δe 可使简化法与迭代法的计算结果非常接近；（6）随着δe的增大，平均法计算的ωp与迭代法计算的ωp差距越来越大。综上分析可知，三种方法（迭代法、平均法、简化法）都可以计算活塞角速度，但其特点和适用范围不同：（1）迭代法计算的ωp值精确（如图1 所示）但需要编写较为复杂的程序进行反复迭代（见式2），此方法适用于活塞角速度、压缩机摩擦功耗等参数的理论仿真研究；（2）平均法计算公式简单（见式4），但计算结果为一个比精确值大的恒定值（如图2-图5 所示，平均法计算结果为水平线），且计算误差较大，例如，图2 中平均法计算得到的ωp最大绝对误差可达73.58rad/s，而最大相对误差可达146.85%；（3）相比于平均法，简化法计算公式同样简单（见式3），但其优点在于计算的ωp值不仅变化趋势和精确值（即迭代法得到的ωp）相同，且计算精度也明显提高（如图2～图5 所示），例如，图2 中简化法的计算结果与精确值相比，最大绝对误差为28.03rad/s，最大相对误差为45.17%。虽然简化法和平均法计算ωp值的精度都不算很高，但由于两种方法的公式简单，不需要借助程序迭代而可以方便地应用于人工计算，两种方法可联立用于压缩机的设计，平均法计算ωp的结果可作为活塞角速度的上极限，简化法的结果可以作为活塞角速度的下极限（绝大部分情况下简化法的计算结果小于精确值），且简化法还可以预测活塞角速度的变化趋势。