滑模方法在分布式电动车容错控制上的应用
2021-03-05陈瑞楠杨鄂川
欧 健,陈瑞楠,杨鄂川,张 勇
(1.重庆理工大学车辆工程学院,重庆400054;2.重庆理工大学机械工程学院,重庆400054)
1 引言
四轮独立驱动的分布式电动车相较于传统汽车而言由于其系统构成简单、输出响应迅速、各车轮能独立进行控制等特点,越来越受到研究者们的关注[1]。但因为其自身驱动系统的特点,在驱动系统失效的情况下容易发生诸如导致跑偏、动力学特性改变等的情况[2]。为改善分布式电动车驱动系统失效发生时的车辆性能,有学者提出在故障发生时关闭故障驱动器与其对应驱动器的方法以维持车辆稳定性,但该方法极易导致车辆动力性下降[3]。文献[4]中提出一种基于分配规则的容错控制方法,该方法能够对系统剩余驱动力进行分配,但控制器性能与故障信息的准确性密切相关,在故障观测结果不精确或延迟的情况下,控制器性能会表现出极大的下降[5]。因此如今已有国内外学者将鲁棒、自适应等的被动容错控制方法应用于飞机、卫星等设备上[6],以弥补故障信息失真引起的控制性能下降。针对分布式电动车驱动系统失效发生时,由于故障信息不准确或未知导致的普通容错控制方法性能下降的问题,设计了一种基于滑膜变结构控制理论的被动容错控制方法,针对参考横摆角速度和质心侧偏角信号的跟踪问题,设计了一种协调分配的上层容错运动控制器,以求得当前车辆所需附加横摆力矩。同时,考虑可能发生的故障对控制器收敛性进行讨论,以求出能够满足容错控制需求的控制器参数范围。下层驱动力分配控制器使用名义分配的方法对各轮驱动扭矩进行分配,以期合理分配各轮驱动力,满足车辆纵横向力需求。
2 控制器设计
车辆稳定控制主要涉及轨迹保持与稳定性控制,一般的,汽车的行驶轨迹可以由航向角(由横摆角和质心侧偏角组成)予以描述[7]。若某时刻质心侧偏角较小,则车辆横摆角速度可以决定车辆的稳定状态。若地面附着系数较小,在转向时极易导致质心侧偏角过大,则此时应严格限制车辆质心侧偏角以免车辆失控。由于故障发生时,车辆状态可能发生不可预见的偏差,严重降低车辆安全性,为了修正故障发生时车辆的性能,选取基于滑模变结构控制理论的被动容错控制器,以线性二自由度模型为参考模型,分别使用横摆角速度与质心侧偏角作为参考值计算当前所需控制律,并使用协同控制的方法协调横摆角速度和质心侧偏角的跟踪问题,随后使用名义分配的方法对各车轮转矩进行分配。主要流程,如图1 所示。

图1 被动容错控制结构图Fig. 1 Structure of Passive Fault-Tolerant Control
2.1 上层运动控制器
考虑如下车辆系统:

式中:X=[β r]T—车辆当前质心侧偏角和横摆角速度的状态;Ti=[T1T2T3T4]T—左前、右前、左后、右后轮的输出扭矩;δ—转向轮转角;A、B1与B2为车辆固有参数,其具体数值可以在文献[8]中找到。
若车辆驱动系统发生失效,则表明当前有至少一个车轮无法提供所期望的驱动力矩。假设车辆各车轮输出扭矩与期望输出扭矩Tui之间关系入下:

式中:a、b—质心到前后轴的距离;kf、kr—前后轴侧偏刚度;m—整车质量;vx—车辆速度;I—车辆转动惯量;δ 与△M—前轮转角与附加横摆力矩;△d—由于驱动系统失效而引起的横摆力矩干扰项。
2.1.1 横摆角速度控制

则横摆角速度控制的滑模面可以定义为:
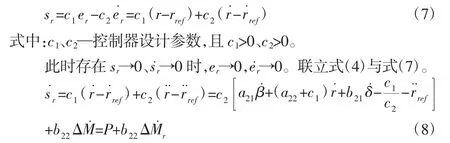
选择饱和函数趋近律,可以得到:

式中:ζr—边界层,可以根据抖振情况选取适当的边界层厚度;εr—控制器设计参数。对式(9)进行积分即可得到横摆角速度控制时维持车辆稳定所需的附加横摆力矩△Mr。
2.1.2 质心侧偏角控制
与上节同理,质心侧偏角控制的滑模面可以定义为:

2.1.3 协调控制
由于横摆角速度与质心侧偏角之间存在着某种耦合关系,因此需要对两个量进行协调控制。选择当质心侧偏角较小时优先跟踪横摆角速度的协调控制方法,选择合适的质心侧偏角边界值β1与β2,则协调控制控制量输出可以表示为:
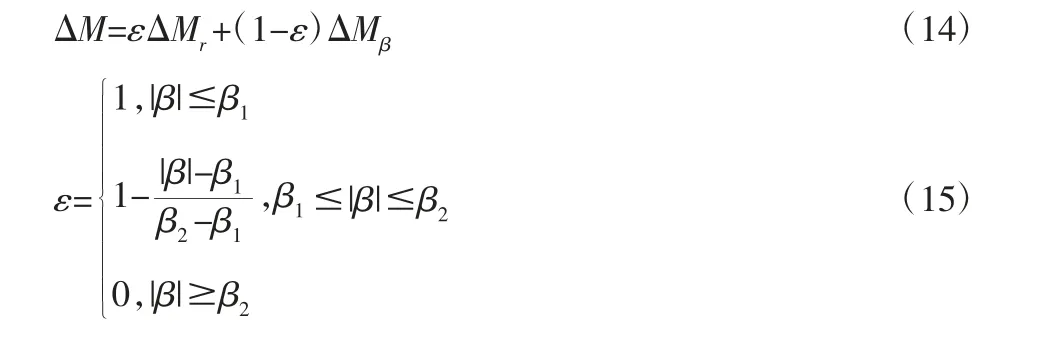
2.2 稳定性证明
将以横摆角速度控制为例,讨论当单个车轮驱动系统发生失效时的控制器稳定性与收敛性。定义Lyapunov 函数为:
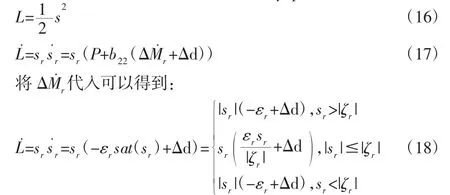
考虑单车轮失效时的极限情况:此时该车轮不输出任何驱动力矩,但剩余车轮全力输出,且车辆状态处于饱和函数的饱和区间内,即|sr|>|ζr|时。可以计算出此时由于驱动系统失效而导致的附加横摆力矩干扰。

2.3 下层转矩分配控制器
采用附着裕度与电机负荷率的加权最优为目标的名义分配策略对各轮转矩进行分配,在分配时假设各轮驱动系统均能够正常输出扭矩,即在分配时不考虑失效的因素,并认为上层控制器能够鲁棒的修正该误差。定义路面附着裕度与电机负荷率可分别由下式表示:

由于目前技术暂不能对车轮侧向力进行直接控制,因此对目标函数进行简化,同时引入加权因子以协调附着裕度与电机负荷率之间的关系,上式可以重新写为:

考虑物理条件对优化求解进行约束

式中:τO、τP—加权系数矩阵;μ—地面附着系数;Fxd—纵向力需求;Fxi、Fvi和Fzi—轮胎纵、侧向力和垂向力。通过最小化目标函数,可以解得当前分配到各车轮的实际控制律Tui。
3 测试与分析
使用NI-PXI 硬件在环测试设备进行试验,以检验所建立的被动容错控制器性能,选取Carsim RT 中的C-class Hatchback 车辆作为试验对象,分别进行开环正弦转向试验与驾驶员在环双移线试验。硬件在环测试设备,如图2 所示。

图2 硬件在环测试设备Fig.2 Hardware-in-Loop(HIL)Test Equipment
3.1 正弦转向输入试验
选取附着系数μ=0.8 的路面,初始车速80km/h,前轮转角,如图3(a)所示。假设在第一秒时,车辆左前轮突然发生ρj1=0.3,σj1=1,Tsul=30 的故障,试验结果,如图3 所示。


图3 正弦转向工况仿真结果Fig.3 Simulation Results of Sinewave Steering Input
从图(3)可以看出,当驱动系统失效发生时,车辆状态较之参考状态之间会产生偏差,此时这里所设计的被动容错控制器能够产生相反方向的附加横摆力矩以弥补故障对车辆状态造成的影响。经过后续正弦转向仿真可以看出,这里所设计控制器能够较好的控制故障车辆跟踪参考横摆角速度与质心侧偏角参考信号。同时,由于在分配各轮转矩时,并未代入车辆当前故障信息进行计算,但从控制器表现可以看出,该控制器能够鲁棒的容忍该误差的存在,即能够鲁棒的容忍故障的发生与故障信息的失准。
3.2 驾驶员在环双移线试验
选取附着系数μ=0.3 的低附着路面,初始车速80km/h,假设驾驶员预瞄时间为1s,反应滞后时间为0.1s,且在第1s 时车辆左前轮完全失效(即输出扭矩为0)。进行驾驶员在环双移线工况仿真试验。仿真结果,如图4 所示。


图4 驾驶员在环双移线仿真结果Fig.4 Simulation Results of Driver-in-Loop Double Line Change
从图3(a)、图3(b)和图3(c)中可以看出,在控制器不参与车辆控制时,车辆将会发生严重侧滑从而导致失控;在控制器参与控制时,车辆能够跟随驾驶员的期望轨迹。这表明这里所设计的被动容错控制器能够改善故障车辆的性能,有效的帮助驾驶员控制车辆跟踪期望轨迹。综上结果表明,这里所设计的基于滑模控制理论的被动容错控制器在故障信息失准的情况下,仍然具有较好的鲁棒性,能够有效地帮助车辆跟踪参考状态信号,能够有效的改善故障车辆性能,提升故障车辆安全性。
4 结语
针对分布式电动车驱动系统失效,但故障信息未知时传统控制方法控制效果不优的问题,介绍了一种基于滑模控制理论的被动容错控制器,以改善故障车辆性能,提升故障车辆安全性。(1)针对车辆驱动系统失效的情况进行了讨论,将驱动系统失效导致的横摆力矩视为横摆力矩干扰引入车辆模型。(2)结合横摆角速度和质心侧偏角,设计了用以对车辆运动进行控制的协调控制上层运动控制器,并对该控制方法的稳定性收敛性进行了讨论,确定了能够使故障车辆稳定的合理控制器参数设计范围。(3)使用名义控制分配的方法对分布式电动车各车轮驱动力矩进行分配,以期在保证满足纵横向力需求的同时,尽可能的优化电机负荷率、地面附着裕度等参数。(4)经过硬件在环试验表明,这里所设计的控制器具有较好的鲁棒性,能够产生与横摆力矩干扰相反的附加横摆力矩,维持故障车辆稳定;并能够有效的跟踪参考信号,改善车辆性能提升车辆安全性。
